Лекция 1 1 ч Элементы квантовой оптики Вопросы

Лекция 1(1 ч). Элементы квантовой оптики

Вопросы: • Интегральные и спектральные характеристики теплового излучения • Законы Кирхгофа, Стефана – Больцмана и Вина • Формула Рэлея - Джинса • Квантовая гипотеза и формула Планка

Интегральные и спектральные характеристики теплового излучения • Природа теплового излучения и его свойства Любой процесс электромагнитного (э/м) излучения связан с потерей энергии (того или иного вида) у источника (излучателя). В зависимости от вида энергии, которую теряет излучатель различают: • тепловое излучение, т. е. испускание э/м волн нагретыми телами за счет их внутренней энергии (причиной излучения является возбуждение атомов, молекул вещества вследствие их теплового движения); • люминесценцию, т. е. излучение (свечение) тел за счет всех других видов энергии (кроме внутренней энергии) или, иначе говоря, это излучение света телами, избыточное над тепловым излучением этих тел. Замечание. В люминесценции различают: • хемилюминесценцию – свечение веществ за счет энергии, выделяемой при химических превращениях; • электролюминесценцию – свечение в газовых разрядах, у поверхностей твердых тел под действием электрического поля; • катодолюминесценцию – свечение твердых тел, вызванное бомбардировкой их электронными пучками; • фотолюминесценцию – свечение тел за счет поглощенного света

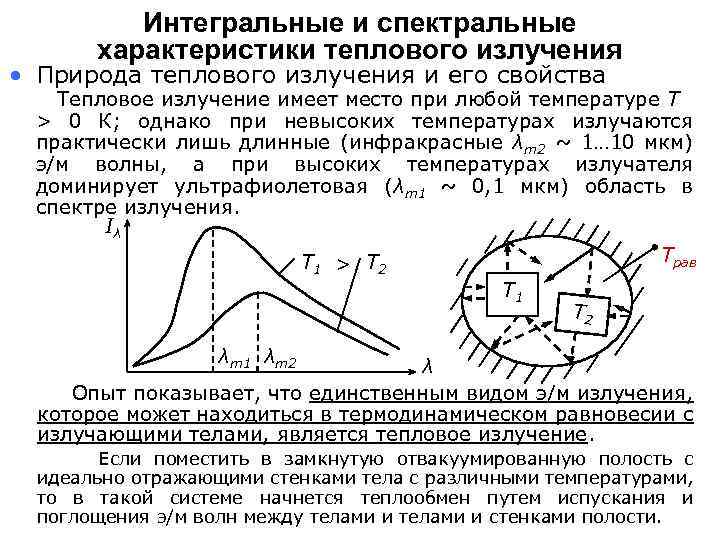Интегральные и спектральные характеристики теплового излучения • Природа теплового излучения и его свойства Тепловое излучение имеет место при любой температуре Т > 0 К; однако при невысоких температурах излучаются практически лишь длинные (инфракрасные λm 2 ~ 1… 10 мкм) э/м волны, а при высоких температурах излучателя доминирует ультрафиолетовая (λm 1 ~ 0, 1 мкм) область в спектре излучения. Iλ Трав T > T 1 2 T 1 T 2 λm 1 λm 2 λ Опыт показывает, что единственным видом э/м излучения, которое может находиться в термодинамическом равновесии с излучающими телами, является тепловое излучение. Если поместить в замкнутую отвакуумированную полость с идеально отражающими стенками тела с различными температурами, то в такой системе начнется теплообмен путем испускания и поглощения э/м волн между телами и стенками полости.

• Интегральные и спектральные характеристики теплового излучения Природа теплового излучения и его свойства Через некоторое время (оно зависит от свойств излучателей и их исходного неравновесного состояния) неизбежно установится термодинамическое равновесие в этой системе, соответствующее определенной температуре Трав. За любой промежуток времени испускаемая телами энергия становится равной поглощаемой энергии, и плотность энергии излучения в пространстве между телами достигает определенной величины, соответствующей Трав. Такое состояние излучения в полости остается неизменным во времени (в отсутствии внешних воздействий). Способность теплового излучения находиться в равновесии с излучающими телами обусловлена тем, что его интенсивность возрастает при увеличении температуры. Всякое нарушение равновесия в системе «тело – излучение» вызывает возникновение процессов, восстанавливающих равновесие (см. принцип Ле Шателье – Брауна)

Интегральные и спектральные характеристики теплового излучения • Энергетическая светимость Интенсивность теплового излучения будем характеризовать мощностью, излучаемой с единицы поверхности тела. Энергетической светимостью Rэ называется величина, измеряемая потоком э/м излучения Фэ, испускаемым единицей поверхности тела (с температурой Т) по всем направлениям (в пределах телесного угла 2π, т. е. в полусферу): Rэ = Фэ /S, [Вт/м 2] (1) где S – площадь излучающей поверхности. S; T Замечание. Энергетическая светимость характеристика теплового излучения. – интегральная

Интегральные и спектральные характеристики теплового излучения • Испускательная способность Тепловое излучение слагается из волн различных частот ω или длин, в основном в оптическом диапазоне: λ ≈ 0, 01… 1000 мкм, и имеет сплошной спектр. Распределение энергии в спектре излучения описывается спектральной плотностью энергетической светимости или испускательной способностью тела: rω, T = d. Rω, T /dω, [Дж/м 2. рад] (2) где d. Rω, T - мощность излучения, испускаемая в узком спектральном интервале dω единицей поверхности при заданной Т. Испускательная способность зависит от температуры Т и частоты ω (или длины волны λ), т. е. является функцией: rω, T = f(ω, T) (или функцией: rλ, T = f’(λ, T)). Если известна функция rω, T, то энергетическая светимость может

Интегральные и спектральные характеристики теплового излучения

Интегральные и спектральные характеристики теплового излучения Определение. Тело, у которого поглощательная способность аω, T = 1, называется абсолютно чёрным. Реальные тела, для которых аω, T < 1, называются серыми. • Модель абсолютно чёрного тела (АЧТ) Т = const Почти замкнутая полость с малым отверстием, через которое проникает внутрь излучение (тепловой луч). уч л Температура стенок поддерживается АЧТ постоянной. Попавшее излучение после многократных отражений от внутренних стенок практически полностью поглотится ими. Поэтому само малое отверстие можно принять за АЧТ, так как для него аω, T = 1 (отверстие полностью поглотило излучение). Замечание. Сажа и платиновая чернь по своим оптическим характеристикам приближаются к АЧТ. Эксперимент показывает, что тело, испускающее больше лучистой энергии, должно и больше поглощать, т. е. обладать большей аω, T. Это следствие равновесности теплового излучения.

Закон Кирхгофа • Закон установлен в 1859 г. немецким физиком Густавом Кирхгофом; он также предложил модель АЧТ. Формулировка. Отношение испускательной способности к поглощательной способности не зависит от природы тела (вещества) и является для всех тел одной и той же (универсальной) функцией частоты (или длины волны) и температуры. где - испускательная способность АЧТ (т. к. = 1). Вывод. Зная испускательную способность АЧТ, и определив экспериментально спектральный коэффициент поглощения для рассматриваемого тела, можно определить испускательную способность этого тела (как серого тела):

Закон Стефана – Больцмана • • В 1879 г. Йозеф Стефан, австрийский физик, анализируя экспериментальные данные по излучению реальных (серых) тел, пришел к выводу, что энергетическая светимость Rэ любого тела пропорциональна четвертой степени абсолютной температуры. Однако последующие более точные измерения показали ошибочность его выводов. Людвиг Больцман в 1884 г. , исходя из термодинамических соображений, получил теоретически выражение для энергетической светимости АЧТ: где σ = 5, 67. 10– 8 Вт/(м 2. К 4)– постоянная Стефана – Больцмана. Замечание. Для серых тел закон излучения должен быть дополнен поправочным коэффициентом ε = RЭсер / RЭ 0 < 1, который часто называют степенью черноты. Поэтому закон (5) принимает вид: RЭсер = . σ. Т 4 (51)

Закон смещения Вина • В 1893 г. немецкий астрофизик Вильгельм Вин, воспользовавшись, кроме термодинамики, также электромагнитной теорией, показал, что универсальная функция Кирхгофа должна иметь вид: f(ω, T) = ω3. F(ω/T) (6) где F(ω/T) – некоторая функция отношения частоты излучения к температуре. Замечание. Выражение вида (6) называют формулой Вина. Если воспользоваться формулой преобразования то можно получить (6) в виде функции f ′(λ, T): последнюю формулу преобразуем к виду где ψ(λ. Т) некоторая функция (λ. Т).

Закон смещения Вина Если последнюю формулу для f ′(λ, T) продифференцировать по λ и полученное выражение приравнять к « 0» : где λm - значение λ, отвечающее экстремуму функции, а функция - другая, аналогичная функция. Тогда, определяя экстремум из уравнения (из опыта известно, что λm ≠ 0); следовательно решение последнего уравнения дает некоторое число «b» : (7) записать в виде закона «смещения» Вина: (8) Формулировка. Длина волны в спектре излучения АЧТ, соответст -вующая наибольшей испускательной способности λm, обратно пропорциональна абсолютной температуре Т тела.

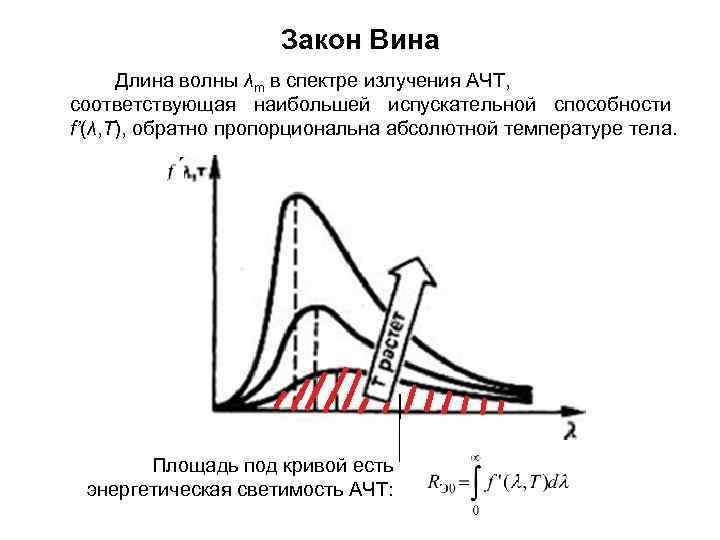Закон Вина Длина волны λm в спектре излучения АЧТ, соответствующая наибольшей испускательной способности f’(λ, T), обратно пропорциональна абсолютной температуре тела. Площадь под кривой есть энергетическая светимость АЧТ:

Формула Рэлея – Джинса Джон Рэлей и Джеймс Джинс в 1900 – 1909 г. г. (независимо), исходя из теоремы классической статистической физики о равнораспределении энергии по степеням свободы и предписывая каждому колебанию, связанному с электромагнитной волной излучения, среднюю энергию = k. T, получили выражение для универсальной функции Кирхгофа (или испускательной способности АЧТ): (9) где k = 1, 38. 10– 23 Дж/К – постоянная Больцмана. Интегрирование этой функции по λ в пределах [0; ∞] дает бесконечное значение. Этот результат, получивший в свое время название «ультрафиолетовой катастрофы» , находится в противоречии с опытом. Равновесие между излучением и излучающим телом устанавливается при конечных значениях плотности лучистой энергии.

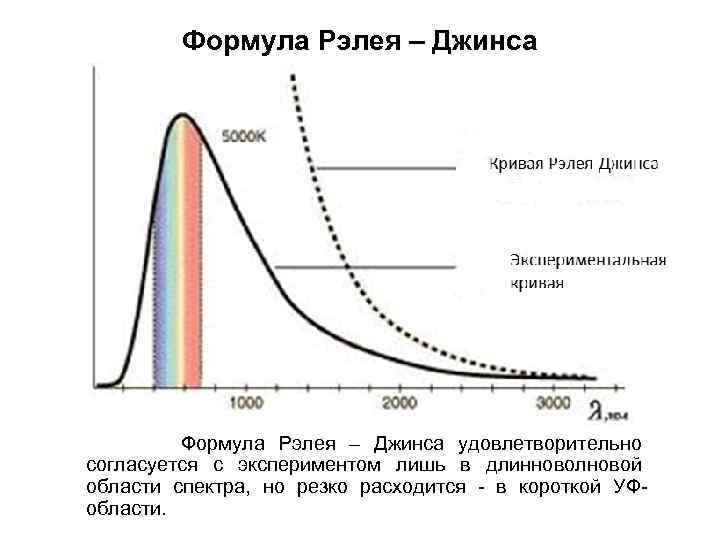Формула Рэлея – Джинса удовлетворительно согласуется с экспериментом лишь в длинноволновой области спектра, но резко расходится - в короткой УФобласти.

Квантовая гипотеза и формула Планка В 1900 г. , исследуя проблему теплового излучения, Макс Планк высказал гипотезу о том, что излучение испускается телами не непрерывно, а порциями (или квантами) энергии, величина которых пропорциональна частоте излучения: или (10) где h = 6, 62. 10– 34 Дж. с, ħ = h/2π = 1, 055. 10– 34 Дж. с - постоянная Планка. Замечание. Так как размерность постоянной Планка «энергия х время» - совпадает с размерностью величины, которую в механике называют «действием» , то h часто называют «квантом действия» . Замечание: В механике: «действие» (по Гамильтону) - это

Квантовая гипотеза и формула Планка Гипотеза Планка о квантах нарушила незыблемое правило классической физики о том, что любая физическая величина, в том числе и энергия (излучения), изменяется непрерывным образом, т. е. за бесконечно малый промежуток времени ее изменение всегда бесконечно мало. Именно гипотеза Планка положила начало квантовой теории (квантовой физике) - современной физической теории, в которой идея квантования (т. е. дискретности) распространяется на различные физические величины, характеризующие состояние системы. Если излучение испускается квантами (порциями) , то полная энергия Eп излучения должна быть кратной этой величине, т. е. в общем случае: (11) где n = 0, 1, 2, 3, …

Квантовая гипотеза и формула Планка В состоянии равновесия (в котором находится тепловое излучение) распределение колебаний по значениям энергии, как известно, подчиняется закону Больцмана; и тогда вероятность Pn - того, что энергия колебания с частотой ω имеет значение En, определится выражением: (12) где Nn – число колебаний с энергией En, N – полное число колебаний. Зная вероятность Pn появления различных значений энергии колебания, можно найти среднее значение этой энергии .

Квантовая гипотеза и формула Планка Замечание. Согласно теории вероятностей: Введя вспомогательную переменную x = ħω/k. T (последняя, допустим, может принимать непрерывный ряд значений), преобразуем выражение для средней энергии с учетом правила взятия дифференциала логарифма: Примечание. геометрической – сумма членов убывающей бесконечной прогрессии знаменателем exp(-x) с первым членом, равным 1, и

Квантовая гипотеза и формула Планка Заменив x на его значение ħω/k. T, получим окончательно выражение для средней энергии излучения с частотой ω: (13)

Квантовая гипотеза и формула Планка • Формулы Планка для АЧТ Перемножив (13) и (14) получим объемную плотность энергии, приходящуюся на интервал частот dω: а разделив последнее выражение на dω, получим спектральную плотность (объемную) энергии равновесного теплового излучения: Универсальная функция Кирхгофа f(ω, T) (или, иначе, испускательная способность АЧТ r 0ω, T) связана с функцией w(ω, T):

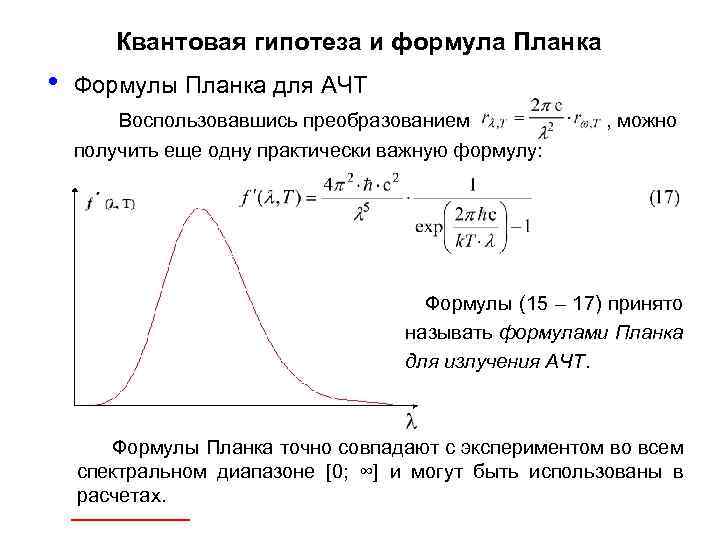Квантовая гипотеза и формула Планка • Формулы Планка для АЧТ Воспользовавшись преобразованием получить еще одну практически важную формулу: , можно Формулы (15 – 17) принято называть формулами Планка для излучения АЧТ. Формулы Планка точно совпадают с экспериментом во всем спектральном диапазоне [0; ∞] и могут быть использованы в расчетах.

Квантовая гипотеза и формула Планка С помощью формулы (16) (или (17)) можно получить все известные законы теплового излучения, а также - значения физических констант σ, b. • Так, определяя энергетическую светимость АЧТ через функцию Планка: и используя подстановку , => ; => – закон Стефана-Больцмана, где

Квантовая гипотеза и формула Планка • Если продифференцировать по λ функцию Планка вида (17), т. е и приравнять производную « 0» , то экстремум функции f′(λ, T) определим по выражению {…} = 0. Введя обозначения трансцендентное уравнение: после нахождения его корня легко определить константу Вина b:

Квантовая гипотеза и формула Планка • Дополнительно можно показать универсальность функции Планка, а именно: а) при ħɷ << k. T (малые частоты – длинные волны) функция Планка превращается в функцию Рэлея - Джинса: [здесь использована формула б) при ħ >> k. T (большие частоты – короткие волны) функция Планка превращается в формулу Вина f(ω/T): [здесь учтено, что