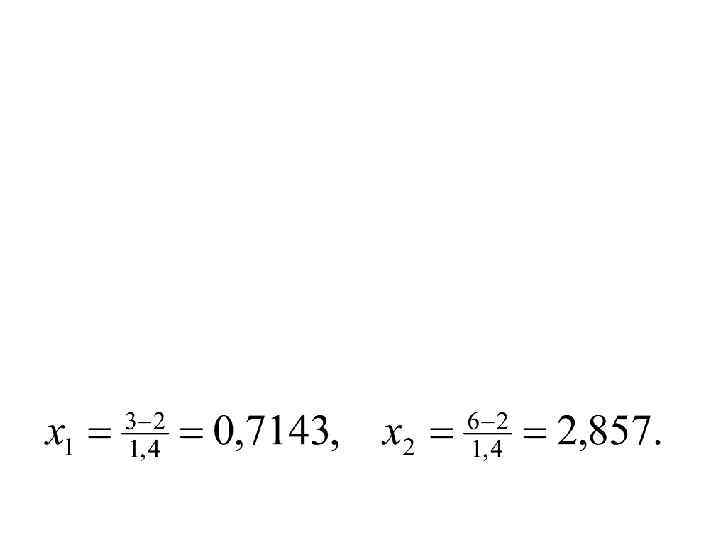Лекции по теории вероятностей для студентов 2 -го

Лекции по теории вероятностей для студентов 2 -го курса ИЭФ

Литература: 1. Виленкин. Комбинаторика 2. Гмурман. Теория вероятностей и математическая статистика 3. Вентцель. Теория вероятностей 4. Красс и Чупрынов. Основы математики и. . . 5. Карпелевич и Рогов. Комбинаторика и бином Ньютона. Метод. указания 6. Гмурман. Руководство к решению задач. . . 7. Вентцель и Овчаров. Теория вероятностей

8. п/р Свешникова. Сб. задач по теории вероятностей. . . 9. Карпелевич. Статистика. Метод. Указания 10. Кочнева и Павлова. Теория вероятностей и математическая статистика

1. Комбинаторика 2. 1. 1. Размещения 3. Определение. Пример:

Пример: Из группы 25 человек выбирают старосту. Профорга и культорга. Ск. способов?

1. 2. Перестановки Определение. Пример: Ск. способами можно за стол президиума посадить 8 человек?

1. 3. Сочетания Определение. Пример: Ск. способами можно из 25 человек выбрать троих на конференцию?

1. 4. Свойства числа сочетаний. 1. 5. Бином Ньютона

Треугольник Паскаля.

2. Случайные события 3. 2. 1. Классическое определение вероятности 4. 2. 1. 1. Виды событий. Достов. , невозм. , случ. 5. 2. 1. 2. Случаи. Возм. , благопр. событию Примеры: 1. Вероятность выпадения герба при одном бросании монеты.

2. Вероятность выпадения хотя бы одного герба при двух бросании монеты. 3. Вероятность извлечь белый шар из урны. 6 б. 4. и 4 ч. ш. 4. Из той же урны извлекают 2 шара. Найти вероятность того, что они оба белые

5. Колода 36 карт делится пополам. Найти вероятности событий: А – все тузы в одной половине, В – в каждой половине два туза, С – в одной половине один туз, а в другой 3. 2. 2. Статистическое определение вероятности

Пример: 1. Пирсон 1200 бросаний Лаплас 2400 бросаний 2. Частота рождения мальчика - 0, 514

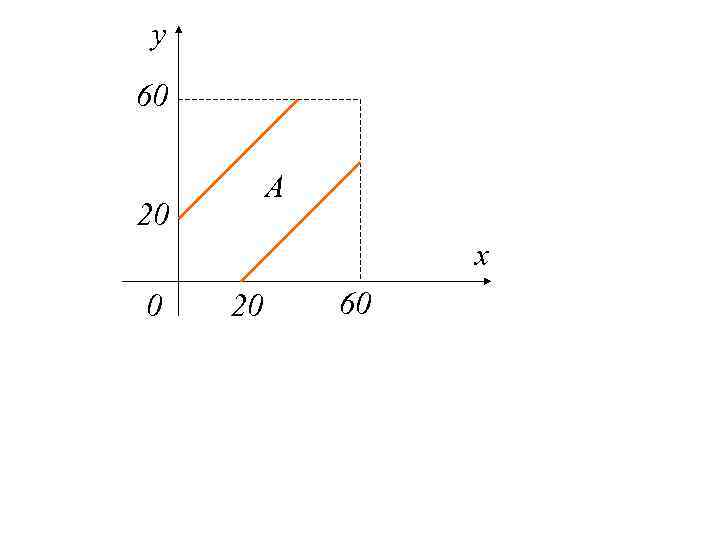
2. 3. Геометрические вероятности Все возможные случаи ↔ геом. мн-во “U” Благоприятные случаи ↔ подмн-во “A” в “U”. Тогда Пример: Танечка и Ванечка договорились встретиться сл. образом: время прихода от 12. 00 до 13. 00 и каждый ждет не более 20 мин. Какова вер-ть встречи?

y 60 A 20 x 0 20 60

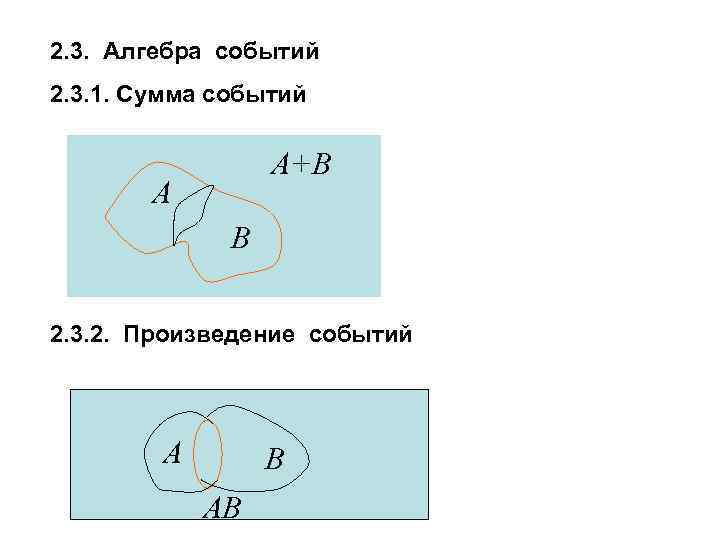2. 3. Алгебра событий 2. 3. 1. Сумма событий A+B A B 2. 3. 2. Произведение событий A B AB

2. 3. 3. Событие, противоположное событию A U – достоверное событие, V – невозможное событие 2. 3. 4. Свойства операций над событиями A,

2. 4. Основные теоремы теории вероятностей 2. 4. 1. Зависимые и независимые события. Определение незавасимости. Условная вероятность Пример: Из колоды 36 карт извлекается 1 карта A -- карта красной масти, B -- карта является тузом, С -- карта является пиковой дамой

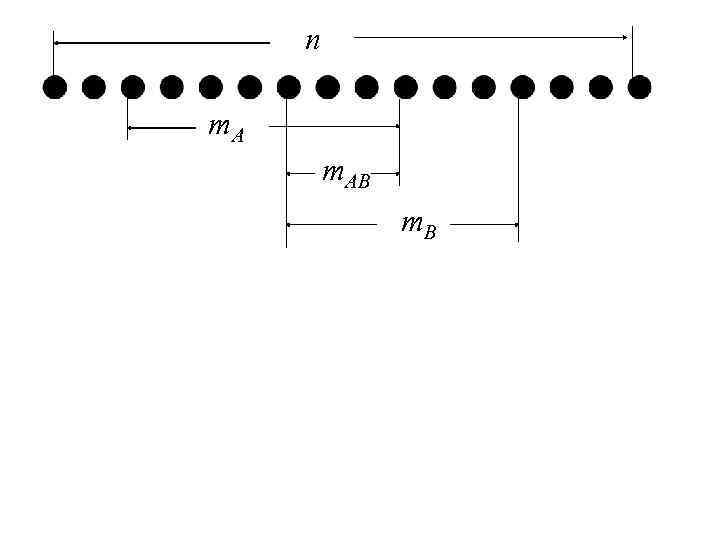
2. 4. 2. Теорема умножения

n m. AB m. B

Примеры: 1. В урне 6 б. и 4 ч. шара. Извлекаются 2 ш. Какова вер-ть того, что они белые?

2. В коробке 9 новых теннисных мячей. Для игры берут 3 и кладут обратно. Какова вер-ть того, что после 3 -х игр все мячи будут игранные? Если A и B независимы, то

Пример. Деталь изготавливается на двух станках без промежуточного контроля. Вер-ти изготовления стандартных деталей на этих станках -- 0, 95 и 0, 9. Какова вер-ть того, что деталь стандартная? 2. 4. 3. Теорема сложения

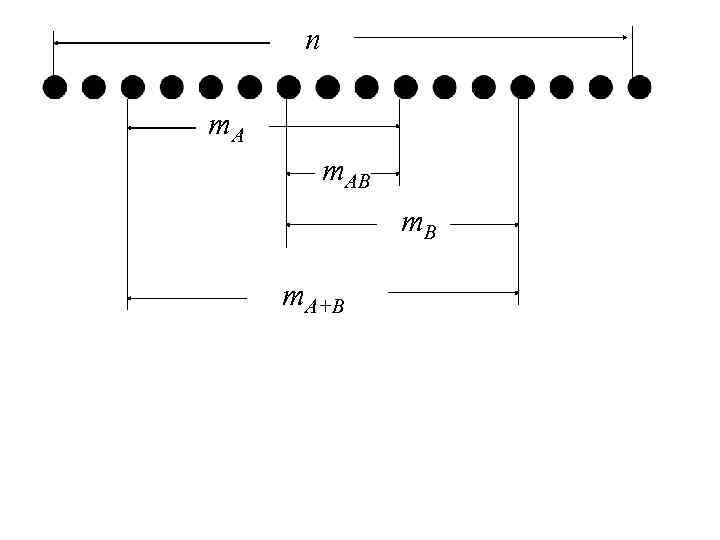n m. AB m. A+B

Пример: Из колоды 36 карт вынимают 1. Какова вер-ть того, что это картинка или карта пиковой масти? Если A и B несовместны, то

Пример: В 1 -ой урне 6 б. и 4 ч. шара, во 2 -ой – 3 б. и 7 ч. шаров. Вынимают по одному шару. Какова вер-ть того, что они одинакового цвета Следствие

Примеры: 1. 2 1 3

Примеры: 2. Два стрелка по очереди стреляют по мишени. Выигрывает тот, кто раньше попадет. Найти вер-ть выигрыша 1 -го. Вер-ти попадания для них p 1=0, 4, p 2=0, 7.

2. 4. 4. Формула полной вероятности H 1 A A Hn

Примеры: 1. В 1 -ой урне 6 б. и 4 ч. шара. Во 2 -ой -- 3 б. и 7 ч. шаров. Из 1 -ой во 2 -ю переложили 1 шар и после этого из 2 -ой извлекают 1 шар. Какова вер-ть того, что он белый?

2. Из полного набора костей домино достают 2 кости. С какой вер-тью их можно приставить друг к другу? 2. 4. 5. Формула Байесса

Пример 1. Из 1 -ой урны (6 б. и 4 ч. ш. ) переложили во 2 -ую (3 б. и 7 ч. ш. ) 1 шар. После этого из 2 -ой урны вынули 1 шар. Он оказался белым. Какова вер-ть того, что переложили белый шар?

Пример 2. В группе из 20 студентов 4 отличника, 8 хороших ст-ов, 5 троечников и 3 двоечника. Отличники знают ответы на все 30 экзаменационных вопросов, хорошие - знают ответы на 25 вопросов, троечники - на 15 вопросов, а двоечники - на 5. Вызванный студент ответил на 3 вопроса и получил «отл» . Каклва вер-ть того, что был вызван действительно отличник? двоечник*? Гипотезы: -вызван отличник - вызван хорошист - вызван троечник - вызван двоечник

- вызванный студент получил «отл»

2. 4. 6. Последовательность независимых испытаний (схема Бернулли).

Пример: Проверяются 10 приборов. Вер-ть того, что прибор исправен 0, 9. Найти вер-ть событий: A -- исправны 8 приборов, B -- исправны не менее 8 приборов, С -- исправен хотя бы 1 прибор.

Локальная теорема Лапласа. Интегральная теорема Лапласа

Пример: Вер-ть рождения мальчика 0, 51. Найти вер -ти событий: А -- Из 100 новорожденных 50 мальчиков, В -- Мальчиков не меньше 25, но не больше 50.

3. Случайные величины 4. 3. 1. Дискретные случайные величины 5. Определение, закон распределения 6. 3. 1. 1. Ряд распределения ξ p x 1 p 1 x 2 p 2 … … xn pn

Примеры: 1. ξ -- число выпадений герба при 1 бросании монеты ξ p 0 0, 5 1 0, 5 2. ξ – число выпадений 5 -ти очков при 3 -х бросаниях игральной кости ξ p 0 1 2 3 (5/6)3 1/2(5/6)2 5/2(1/6)2 (1/6)3

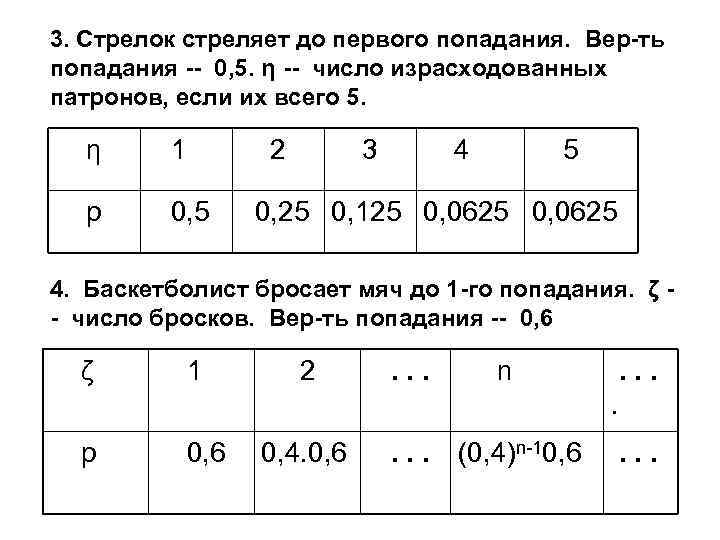3. Стрелок стреляет до первого попадания. Вер-ть попадания -- 0, 5. η -- число израсходованных патронов, если их всего 5. η 1 2 p 0, 5 3 4 5 0, 25 0, 125 0, 0625 4. Баскетболист бросает мяч до 1 -го попадания. ζ - число бросков. Вер-ть попадания -- 0, 6 ζ 1 2 . . . n . . p 0, 6 0, 4. 0, 6 . . . (0, 4)n-10, 6 . . .

Пример: Найти вер-ть того, что баскетболист сделает не меньше 3 -х, но не более 6 -ти бросков (см. предыдущий пример) 3. 1. 2. Функция распределения ○ x

Свойства функции распределения B A ○ x 1 C ○ x 2

Вероятность попадания в интервал B A ○ α C ○ β

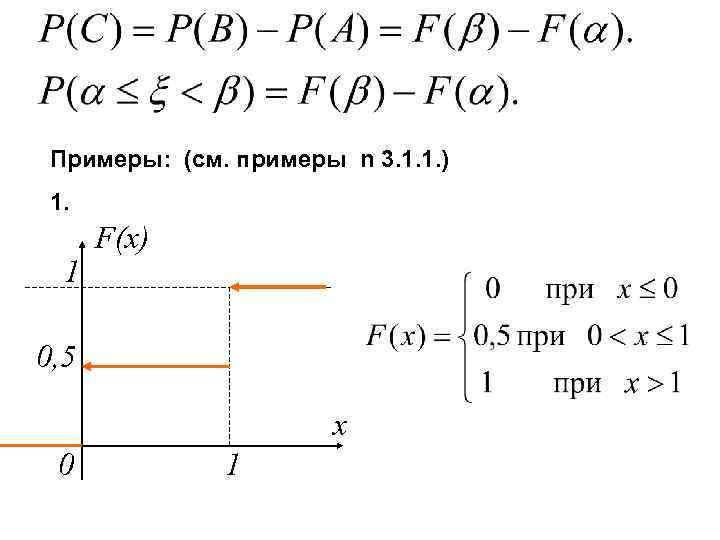Примеры: (см. примеры n 3. 1. 1. ) 1. 1 F(x) 0, 5 x 0 1

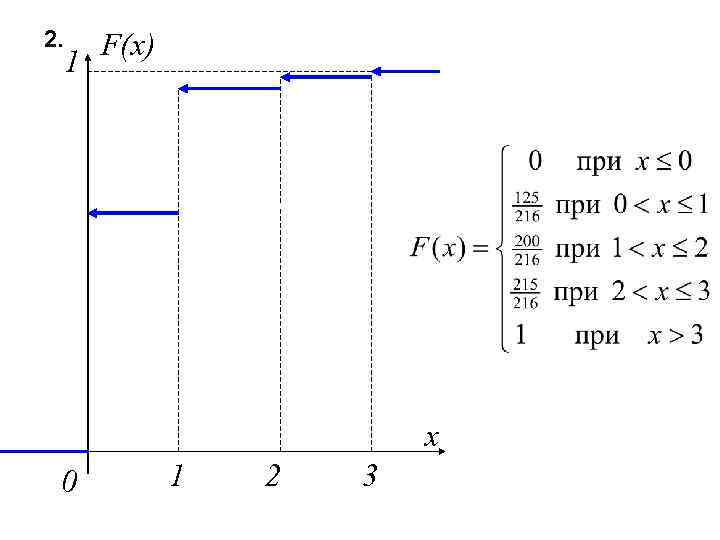2. 1 F(x) x 0 1 2 3

3.

4.

3. 1. 4. Числовые характеристики дискретных случайных величин 1. Математическое ожидание y x 1 x 2 0 p 1 p 2 x 3. . . • Mξ p 3 xn pn x

2. Дисперсия Примеры (см. примеры n 3. 1. 1. ):

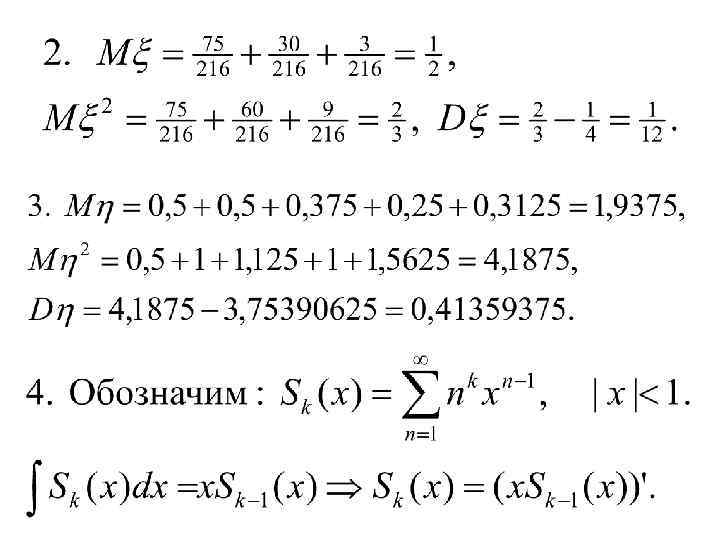
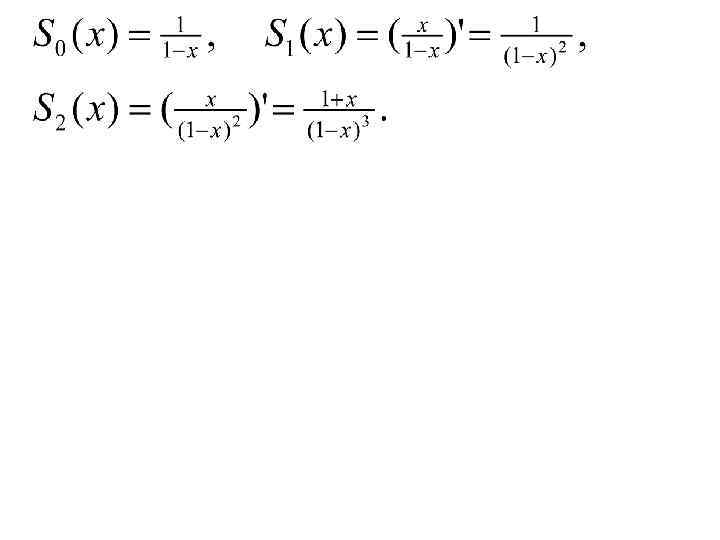
3. Начальные и центральные моменты

3. 1. 5. Биномиальное распределение ξ p Пример: 0 p 0 ξ 1 p 1 . . . m pm -- число успехов в . . . n n pn испытаниях.

Пример: ξ -- число попаданий в мишень при 10 выстрелах. Вер-ть попадания при 1 -м выстреле -- 0, 7. Найти Mξ, Dξ.

3. 1. 6. Распределение Пуассона η 0 1 . . . m . . . p p 0 p 1 . . . pm . . .

Пример. Пуассоновский поток событий плотность потока -- среднее количество событий в ед. времени. λ --

В диспетчерскую поступает 20 заявок в час. Найти вер-ти событий: А -- за 15 мин. поступит не менее 2 -х, но не более 4 х заявок, В -- за 12 мин. поступит хотя бы одна заявка.

3. 2. Непрерывные случайные величины 3. 2. 1. Функция распределения (интегральный закон) Свойства:

B A x C α β 3, 2, 2, Плотность распределения (дифференциальный закон)

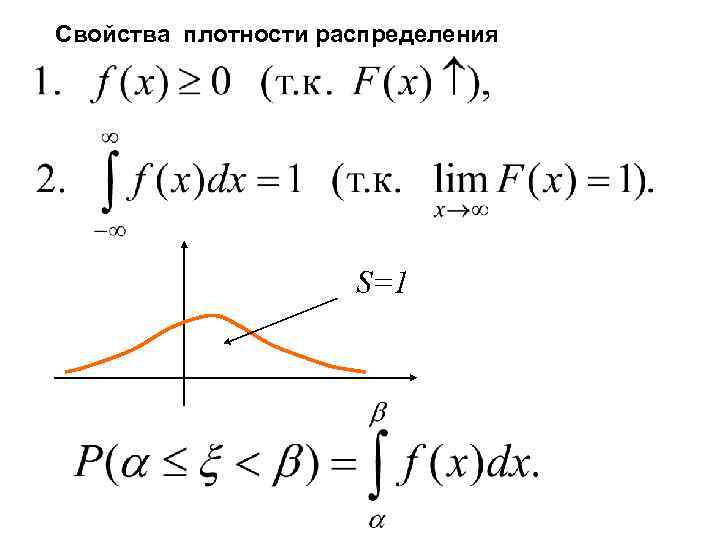Свойства плотности распределения S=1

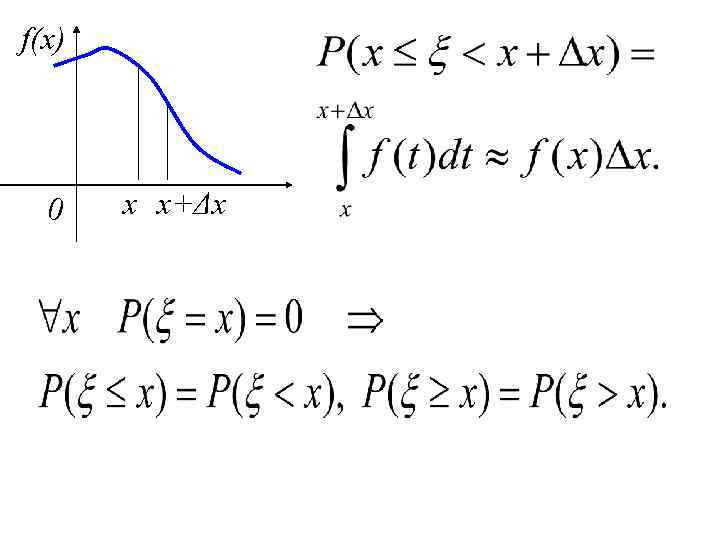f(x) 0 x x+Δx

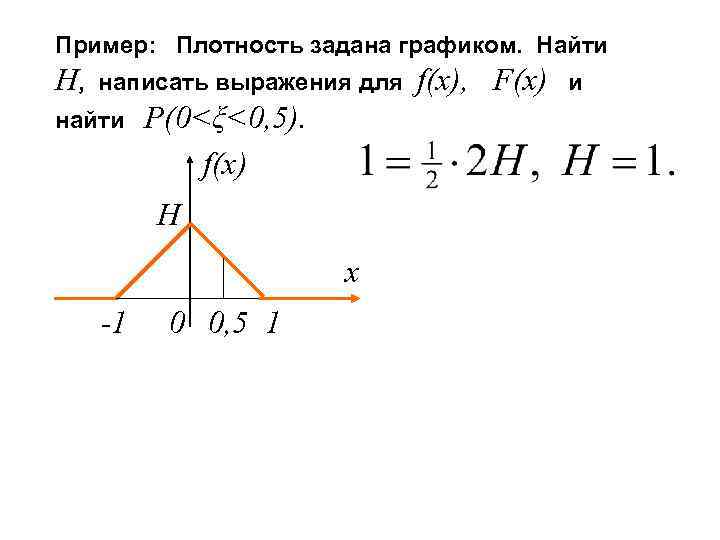Пример: Плотность задана графиком. Найти Н, написать выражения для найти P(0<ξ<0, 5). f(x) H x -1 0 0, 5 1 f(x), F(x) и

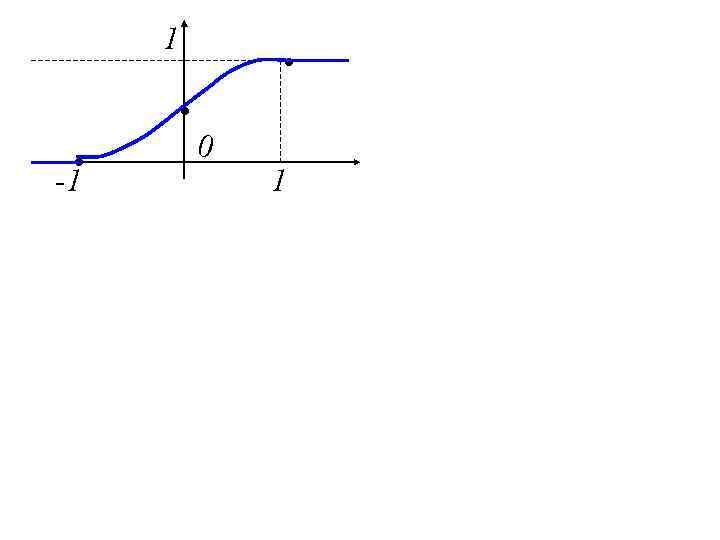1 • • • -1 0 1

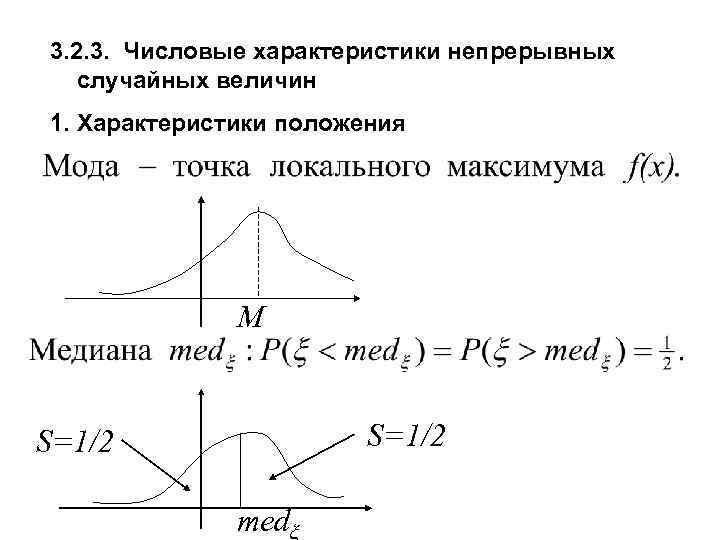3. 2. 3. Числовые характеристики непрерывных случайных величин 1. Характеристики положения М S=1/2 medξ

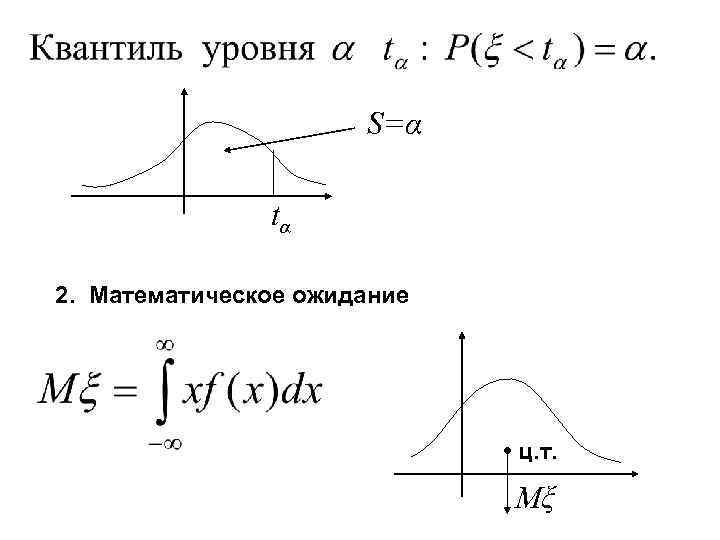S=α tα 2. Математическое ожидание • ц. т. Mξ

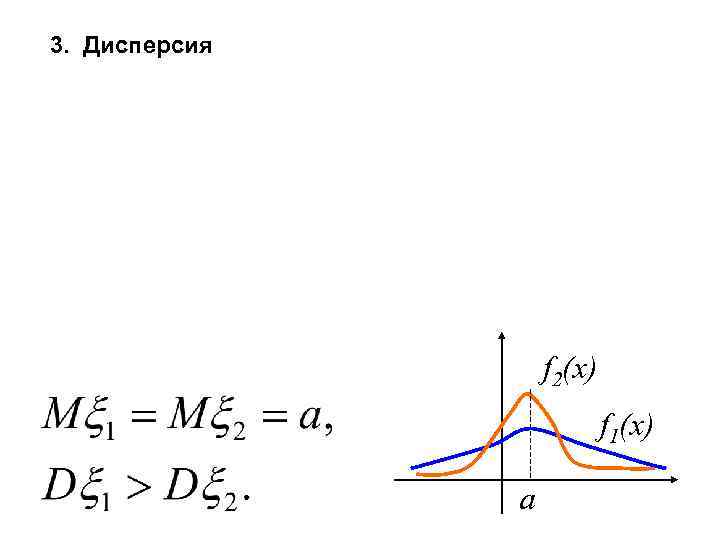3. Дисперсия f 2(x) f 1(x) a

Пример. Найти Mξ и Dξ для распределения примера n 3. 2. 2.

4. Начальные и центральные моменты

3. 2. 4. Равномерное распределение R[a; b]. f(x) 1/(b-a) F(x) 1 a b

Пример. Интервал дв-я автобуса -- 20 мин. Найти вер-сть того, что его придется ждать не менее 5, но не более 12 мин. ?

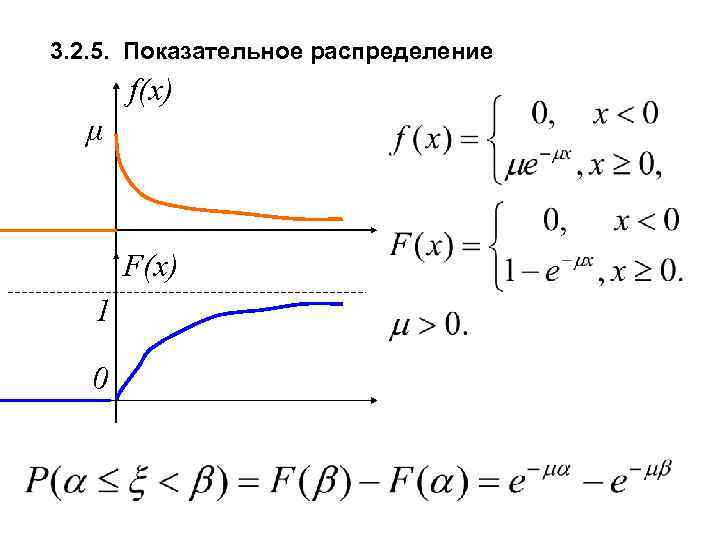3. 2. 5. Показательное распределение f(x) μ F(x) 1 0

Пример. Имеется простейший пуассоновский поток с плотностью потока λ, Найти закон распределения времени ожидания Т следующего события.

Пример. При плотности потока λ=20 заявок в час найти вер-сть того, что ждать следующую придется не менее 12 мин. (См. предыдущий пример). 3. 2. 6. Нормальное распределение (Гаусса)

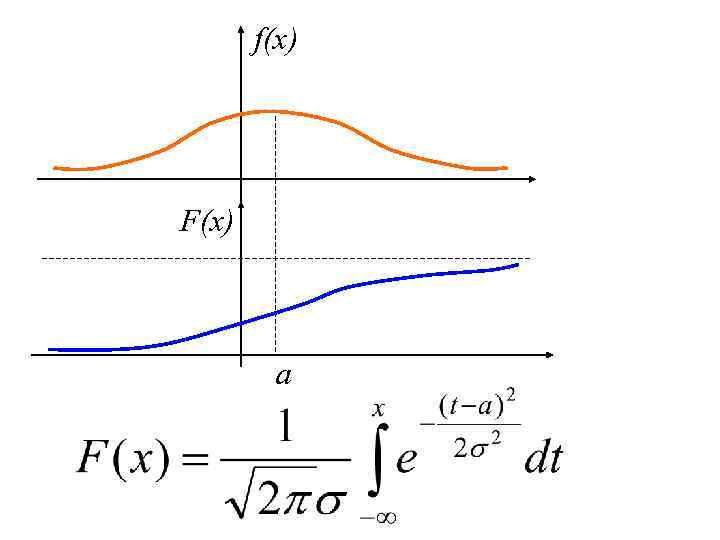f(x) F(x) a

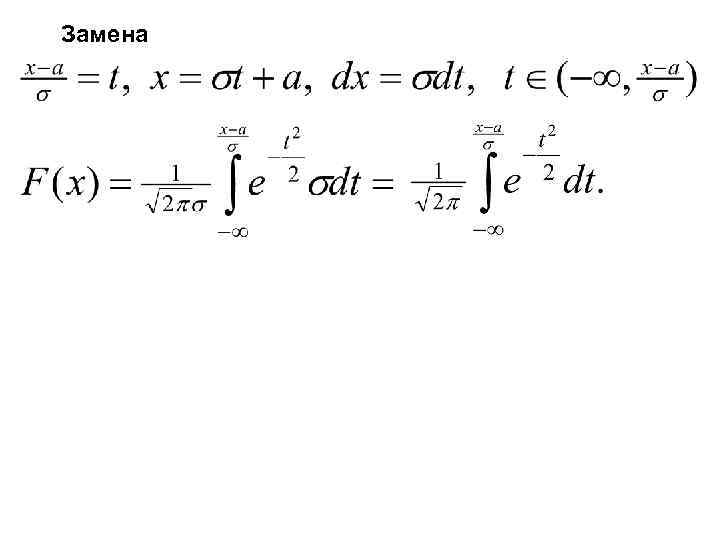Замена

a α β

α a α β a β

Пример: Систематическая ошибка измерения a=5 ед. , а среднеквадратическая σ=20 ед. Найти вер-сть того, что ошибка измерения по модулю не превзойдет 10 ед. Правило 3 -х σ.

4. Двумерные дискретные случайные величины 4. 1. Таблица распределения ξ x 1 x 2 . . . xn p’’ y 1 p 11 p 21 . . . pn 1 p’’ 1 y 2 p 12 p 22 . . . pn 2 p’’ 2 . . . . ym p 1 m p 2 m . . . pnm p’’m p’ p’ 1 p’ 2 . . . p’n η

4. 1. 1. Законы распределения сл. вел. , входящих в систему ξ x 1 x 2 . . . xn p’ p’ 1 p’ 2 . . . p’n η y 1 y 2 . . . ym p’’ 1 p’’ 2 . . . p’’m

Если ξ и η независимы, то Пример: Каждый из 2 -х стрелков стреляет до первого попадания. Вер-сти попадания соответственно 0, 4 и 0, 7, у 1 -го стрелка 4 патрона, у 2 -го -- 3. патронов ξ и η -- числа израсходованных

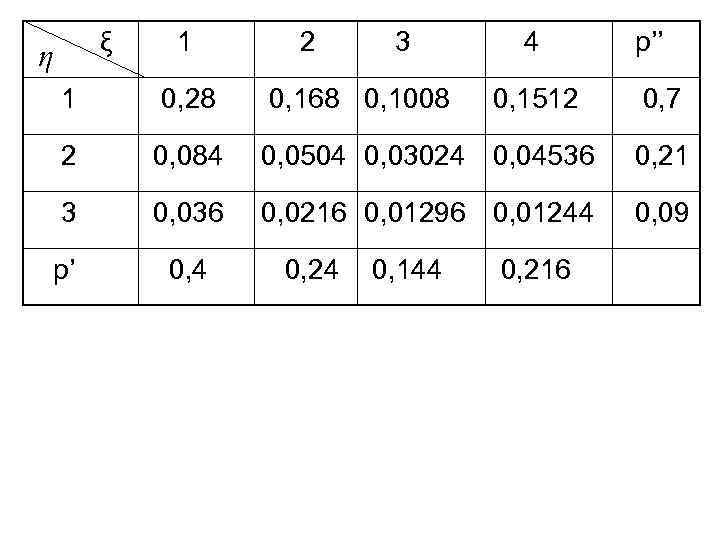ξ η 1 2 3 4 1 0, 28 0, 168 0, 1008 2 0, 084 0, 0504 0, 03024 0, 04536 0, 21 3 0, 036 0, 0216 0, 01296 0, 01244 0, 09 p’ 0, 4 0, 24 0, 144 0, 1512 p’’ 0, 216 0, 7

4. 1. 2. Числовые характеристики двумерной СВ 1. Начальные моменты порядка Аналогично k, l

2. Центральные моменты порядка k, l

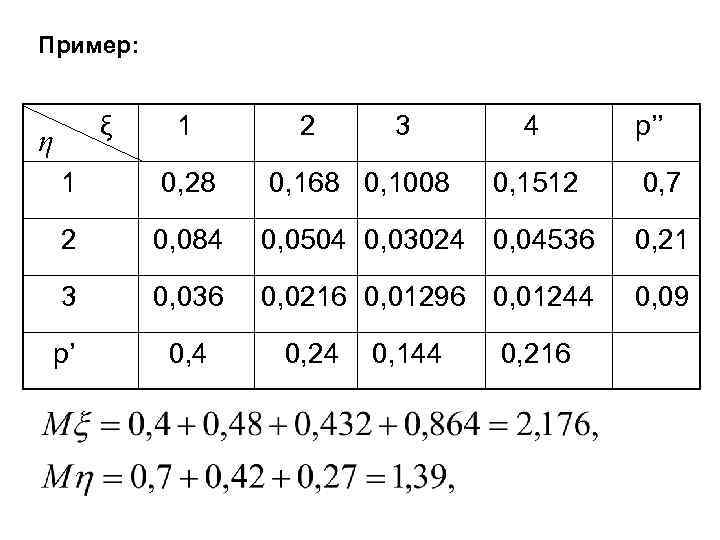Пример: ξ η 1 2 3 4 1 0, 28 0, 168 0, 1008 2 0, 084 0, 0504 0, 03024 0, 04536 0, 21 3 0, 036 0, 0216 0, 01296 0, 01244 0, 09 p’ 0, 4 0, 24 0, 144 0, 1512 p’’ 0, 216 0, 7

Пусть ξ и η независимы. Обратное неверно. Пример: ξ -1 0 1 -1 0 0, 25 1 0 0, 25 0 η

Коэффициент корреляции 4. 2. Условные распределения ξ x 1 x 2 . . . xn

η y 1 y 2 . . . ym 4. 3. Условные математические ожидания. Линии регрессии

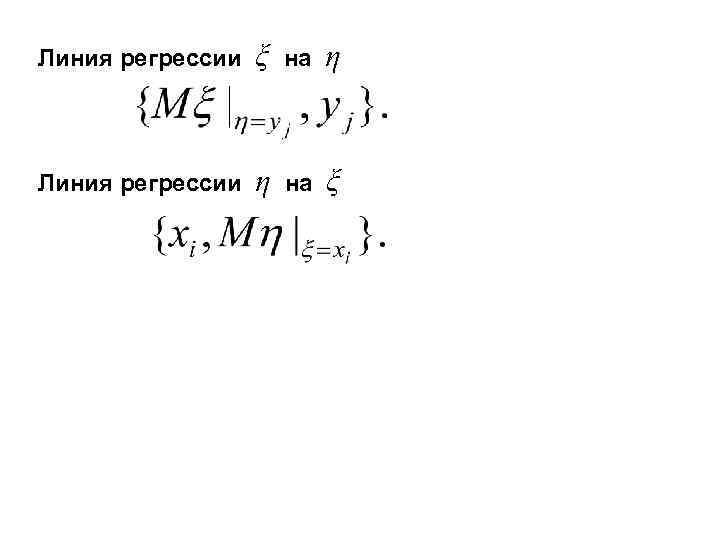Линия регрессии ξ на η Линия регрессии η на ξ

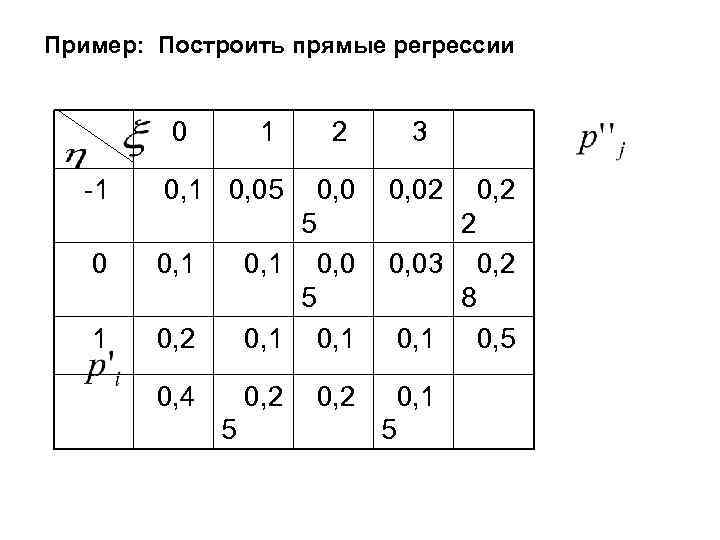Пример: Построить прямые регрессии 0 1 -1 0, 05 0 0, 1 1 2 3 0, 02 0, 0 5 0, 1 0, 4 0, 2 0, 1 5 5 0, 2 2 0, 03 0, 2 8 0, 1 0, 5

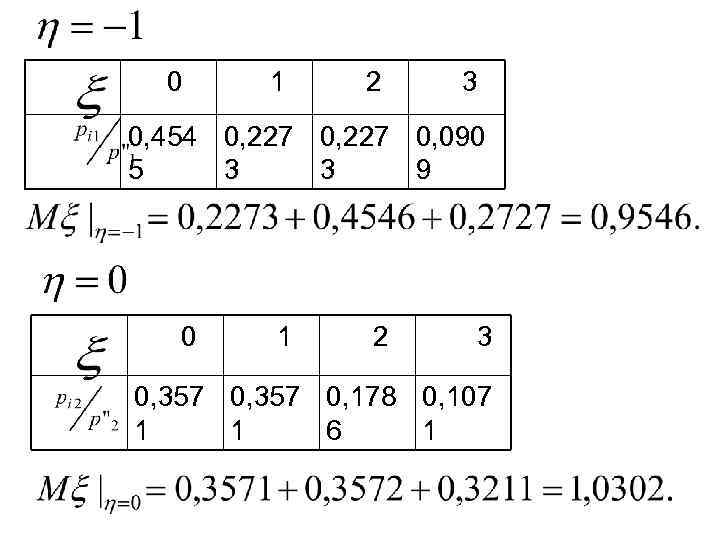0 1 2 3 0, 454 0, 227 0, 090 5 3 3 9 0 1 2 3 0, 357 0, 178 0, 107 1 1 6 1

0 1 2 3 0, 4 0, 2 -1 0 1 0, 25 0, 5

-1 0 1 0, 2 0, 4 -1 0 1 0, 25 0, 5

-1 0, 1333 0 1 0, 2 0, 6667

Регрессия ξ на η 0, 9546 y 1, 0302 -1 0 1, 2 1

Регрессия x η на ξ 0 1 0, 25 0, 2 2 3 0, 25 0, 533 4

• •

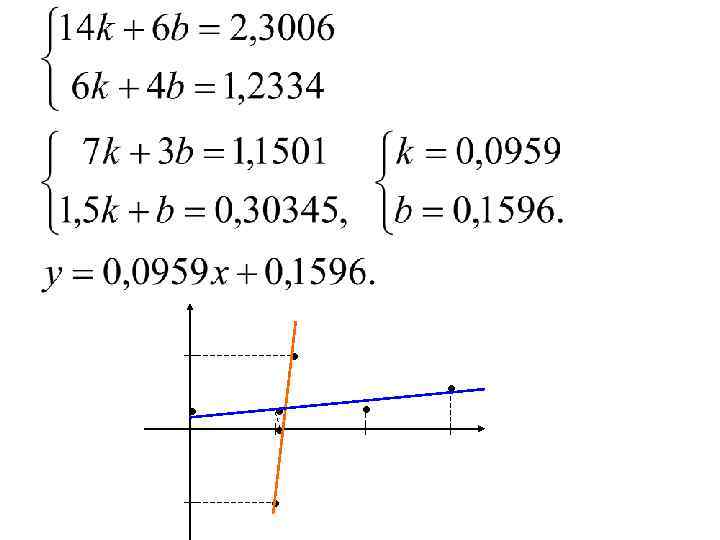4. 4. Нахождение прямых регрессии по числовым характеристикам Задача: найти линейную функцию что Δ=M(η-kξ-b}2 → min y=kx+b такую,

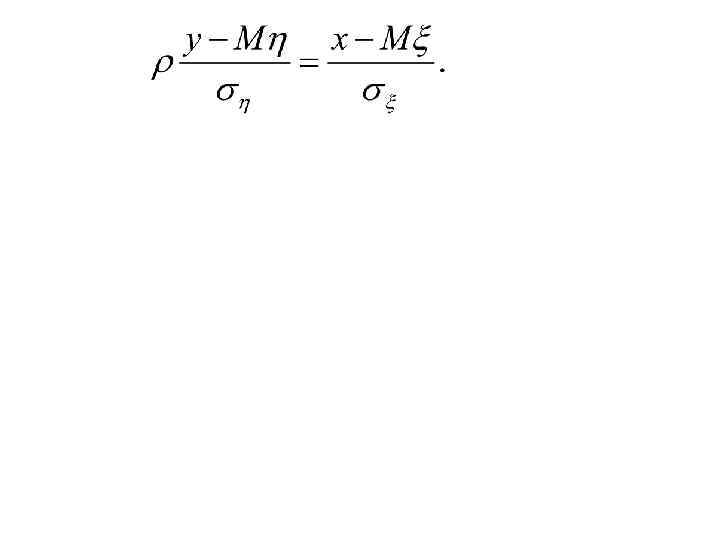
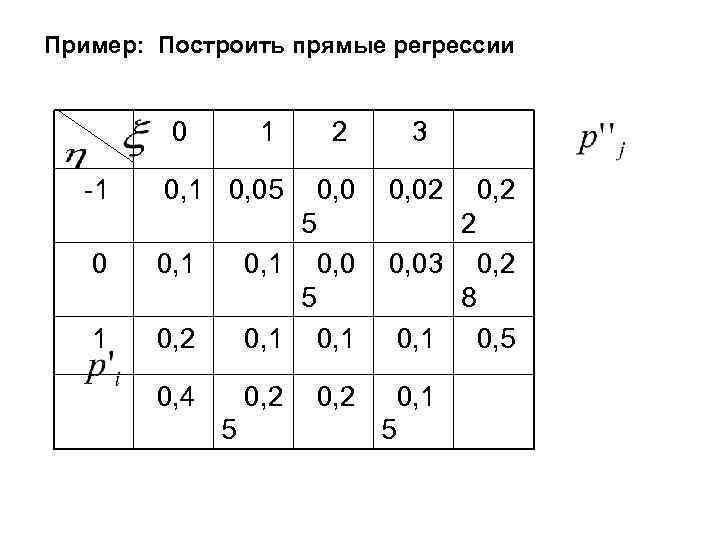Пример: Построить прямые регрессии 0 1 -1 0, 05 0 0, 1 1 2 3 0, 02 0, 0 5 0, 1 0, 4 0, 2 0, 1 5 5 0, 2 2 0, 03 0, 2 8 0, 1 0, 5

5. Функция дискретной СВ 5. 1. Ряд распределения x 1 p x 2 . . . xn p 1 p 2 . . . pn y 1 y 2 . . . yn

Пример. -1 p 0 1 2 3 0, 1 0, 2 0, 3 0, 1 0 -1 0 3 8 0, 2 0, 4 0, 3 0, 1

4. 4. Теоремы о математическом ожидании const p 1

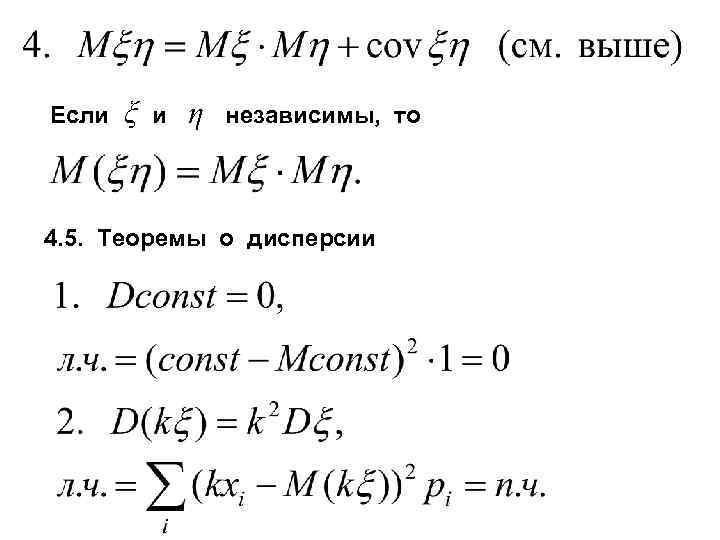Если ξ и η независимы, то 4. 5. Теоремы о дисперсии

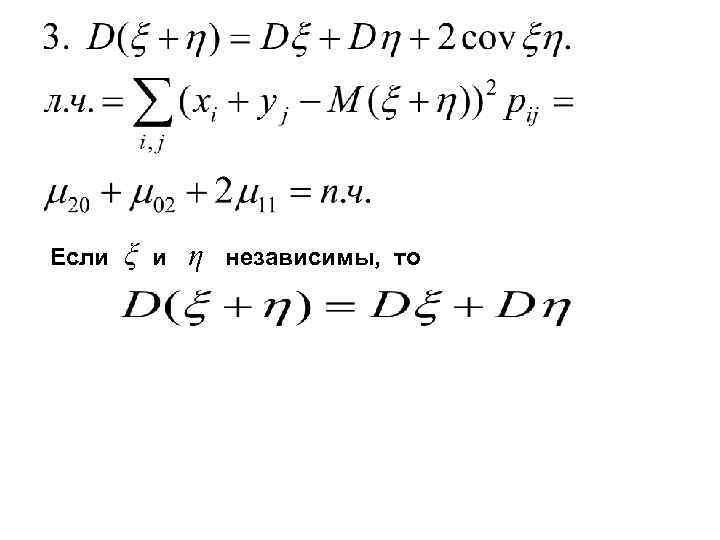Если ξ и η независимы, то

Пример. Mξ, Dξ, ξ -- биномиально распределенная сл. Вел. 0 1 q p

ξ и η. ζ = 2ξ – η, Mζ, Dζ Пример: Даны Найти закон распределения ξ 1 2 3 η -1 0 1 p 0, 5 0, 3 0, 2 p 0, 2 0, 4

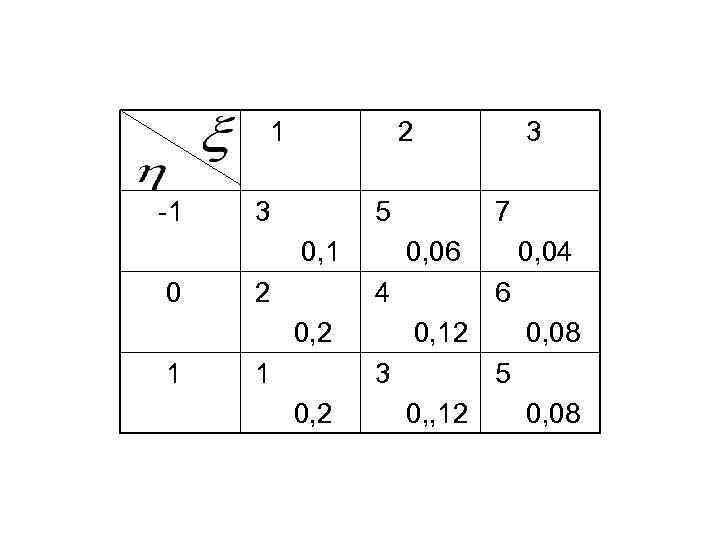1 -1 2 3 5 0, 1 0 2 7 0, 06 4 0, 2 1 1 0, 04 6 0, 12 3 0, 08 5 0, , 12 0, 08

ζ 1 2 3 4 5 6 7 p 0, 2 0. 1 0, 0 2 2 4 8 4

6. Закон больших чисел и центральная предельная теорема 6. 1. Сходимость по вероятности Определение 1. a+ε a a-ε • • • N • •

Определение 2. a+ε a a-ε • • • N Пусть ξ произвольная СВ, имеющая мат. ожидание и дисперсию

6. 2. Неравенство Чебышева.

Пример: Пусть α = 3σ 6. 3. Теорема Чебышева

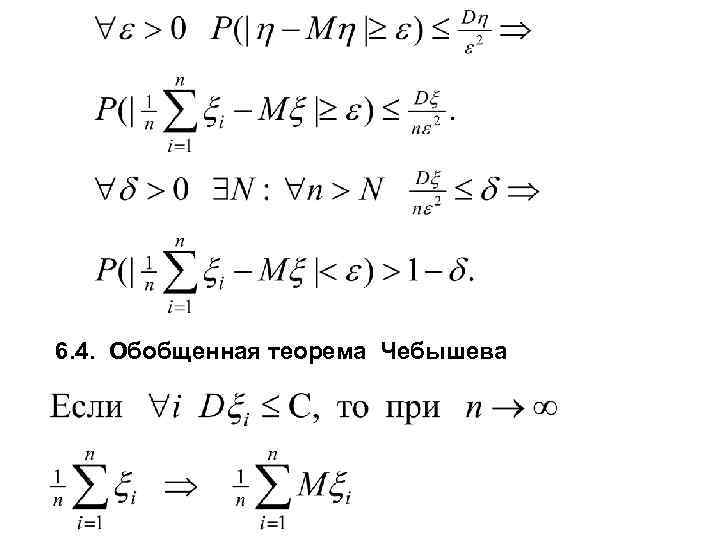6. 4. Обобщенная теорема Чебышева

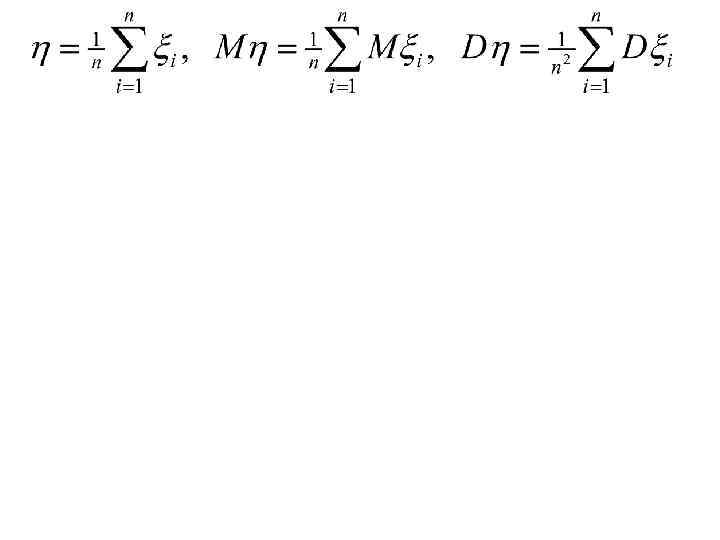
6. 5. Теорема Маркова 6. 6. Следствия: Теорема Бернулли

Теорема Пуассона

6. 7. Центральная предельная теорема в форме Ляпунова

6. 7. Необходимое и достаточное условия применимости ЦПТ (условие Линдеберга)

6. 6. Локальная и интегральная теоремы Муавра. Лапласа Пусть η число успехов в n испытаниях. Тогда

m m+1

Пример. Вероятность брака 100 p=0, 02. Отобрано деталей. Найти вероятности событий А -- 6 бракованные детали. В -- бракованных деталей не меньше 3, но менее 6