Лекции 3 -4 Модели оптического ангармонизма Нелинейные восприимчивости

Лекции 3 -4 Модели оптического ангармонизма. Нелинейные восприимчивости модельных систем 1. Ангармонизм свободного электрона 2. Ангармонизм связанного электрона (модель ангармонического осциллятора) 3. Рамановский ангармонизм (модель Плачека) 4. Вынужденные параметрические эффекты: вынужденное комбинационное рассеяние (Модель Платоненко - Хохлова) 1

1. Ангармонизм свободного электрона Пусть на электрон (заряженную частицу) падает плоская монохроматическая волна: x Ex kz Система уравнений движения электрона при учете магнитной силы Лоренца: z y где - феноменологическая константа затухания, обеспечивающая установление стационарной амплитуды колебаний после включения периодического поля 2

Предположим, что продольное смещение Z при движении частицы мало. Тогда в уравнении движения для координаты X полагаем Z=0 (дипольное приближение, т. е. приближение нулевого порядка по k. Z). Будем искать методом последовательных приближений стационарное решение для смещения электрона в виде ряда Фурье по амплитуде поля: где Первое приближение Пренебрегаем действием магнитного поля (Z 1=0) – отклик электрона линеен. Амплитуда движения заряда вдоль оси X : 3

Найдем линейную поляризуемость электрона: по определению дипольного момента Для перехода от линейной поляризуемости отдельного электрона к линейной восприимчивости газа свободных электронов учтем их объемную концентрацию, N При << Классический радиус электрона 4

Оценка поляризуемости свободного электрона Для оценки поляризуемости в качестве длины волны ЭМ излучения возьмем длину волны, соответствующую потенциалу ионизации атома водорода: - атомный масштаб энергии – постоянная Ридберга. Если вспомнить, что Боровский радиус - т. е. поляризуемость свободного электрона в УФ диапазоне имеет порядок объема атома водорода, или равна по порядку величины поляризуемости 5 связанного электрона вне резонанса.

Второе приближение Теперь в правой части системы уравнений движения электрона берем r(1), а в левые - r(2). Тогда уравнение второго порядка имеет вид: Сила Лоренца определяется следующим выражением « 0» « 2 » и вызывает ангармонизм в динамике свободного электрона, т. к. в ней присутствует осциллирующий член с удвоенной частотой 6

Под действием силы на удвоенной частоте возникают продольные колебания электрона с частотой 2. Амплитуда таких колебаний (вдоль оси Z) : нелинейная поляризуемость свободной частицы – связывает квадрат амплитуды поля и дипольного момента e. Z 2(2) на удвоенной частоте. Для объемной концентрации электронов N переходим к квадратичной (нелинейной) восприимчивости : при >> характерно для магнитных эффектов 7

Т. о. , одним из источников нелинейности вещества является сила Лоренца. - вынужденные колебания вдоль поля (по оси Х(1)(t)) с частотой ; дипольное излучение во все стороны (кроме оси Х); - продольные колебания вдоль оси Z на удвоенной частоте. Максимум интенсивности ВГ – в плоскости XY => такая структура тензора поляризуемости свободного электрона препятствует когерентному сложению амплитуд поля ВГ в макроскопическом образце 8

Оценим величину нелинейной поляризуемости частицы для >> где - т. н. нелинейное поле, т. е. это характерная амплитуда поля, при поле которой линейный и квадратичный отклики одинаковы Квадратичная нелинейность плазмы: 9

2. Ангармонизм связанного электрона: модель ангармонического осциллятора Пусть частица находится в потенциале: где - малый параметр, описывающий отклонение формы потенциальной ямы от параболы. Уравнение движения для электрона в таком потенциале имеет вид: где - затухание; одномерная модель. Пусть внешнее поле – бигармоническое и слабое, Ищем стационарное решение по теории возмущения в виде ряда по : Приравнивая слагаемые одного порядка малости по 10

Первое приближение В первом порядке для смещения : Тогда Поскольку по определению дипольный момент то линейная поляризуемость связанного электрона В результате аддитивного сложения поляризуемостей отдельных частиц можно перейти к восприимчивости 11

12

13

14

Рэлеевское рассеяние света 15

Молекула обладает внутренними степенями свободы. Учтем молекулярные колебания - колебания ядер или ионов "остова" молекулы с частотой Ввиду большой разницы масс ионов остова и электронов (при выполнении условия , где - частота электронного резонанса), колебательное движение может быть отделено от электронного движения и можно говорить о колебательной моде . Справка: и 16

17

18

19

20

21

22

23

24

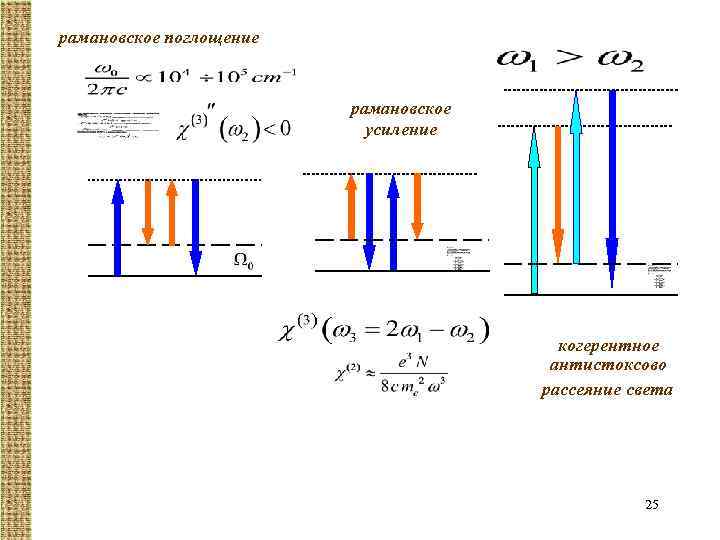рамановское поглощение рамановское усиление когерентное антистоксово рассеяние света 25

26

27