Лекции 14-15_3сем(ЭМПС-14 л)новая версия 2012.ppt
- Количество слайдов: 33
 Лекции 14 -15. Электромагнитная природа света. Интерференция света
Лекции 14 -15. Электромагнитная природа света. Интерференция света
 Вопросы: n Шкала электромагнитных излучений n Краткая историческая справка о развитии взглядов на природу света n Световая электромагнитная волна и ее характеристики n Интенсивность световой волны n Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков n Интерференция света. Разность фаз и оптическая разность хода n Расчет интерференционной картины от двух когерентных источников n Взаимная когерентность световых волн n Пространственно-временная когерентность
Вопросы: n Шкала электромагнитных излучений n Краткая историческая справка о развитии взглядов на природу света n Световая электромагнитная волна и ее характеристики n Интенсивность световой волны n Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков n Интерференция света. Разность фаз и оптическая разность хода n Расчет интерференционной картины от двух когерентных источников n Взаимная когерентность световых волн n Пространственно-временная когерентность
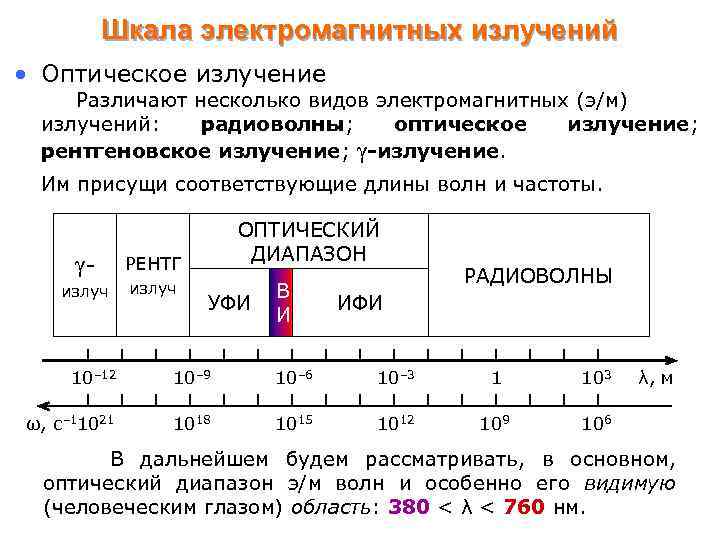 Шкала электромагнитных излучений • Оптическое излучение Различают несколько видов электромагнитных (э/м) излучений: радиоволны; оптическое излучение; рентгеновское излучение; γ-излучение. Им присущи соответствующие длины волн и частоты. γ- РЕНТГ излуч ОПТИЧЕСКИЙ ДИАПАЗОН УФИ В И РАДИОВОЛНЫ ИФИ 10– 12 10– 9 10– 6 10– 3 1 103 ω, с– 11021 1018 1015 1012 109 λ, м 106 В дальнейшем будем рассматривать, в основном, оптический диапазон э/м волн и особенно его видимую (человеческим глазом) область: 380 < λ < 760 нм.
Шкала электромагнитных излучений • Оптическое излучение Различают несколько видов электромагнитных (э/м) излучений: радиоволны; оптическое излучение; рентгеновское излучение; γ-излучение. Им присущи соответствующие длины волн и частоты. γ- РЕНТГ излуч ОПТИЧЕСКИЙ ДИАПАЗОН УФИ В И РАДИОВОЛНЫ ИФИ 10– 12 10– 9 10– 6 10– 3 1 103 ω, с– 11021 1018 1015 1012 109 λ, м 106 В дальнейшем будем рассматривать, в основном, оптический диапазон э/м волн и особенно его видимую (человеческим глазом) область: 380 < λ < 760 нм.
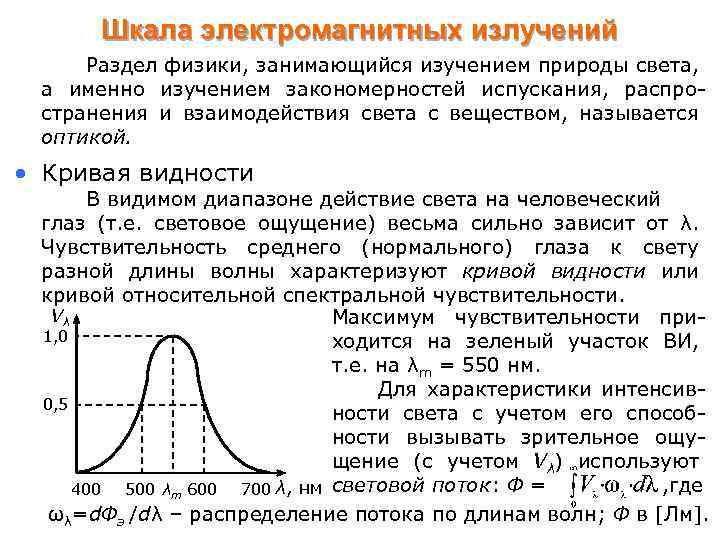 Шкала электромагнитных излучений Раздел физики, занимающийся изучением природы света, а именно изучением закономерностей испускания, распространения и взаимодействия света с веществом, называется оптикой. • Кривая видности В видимом диапазоне действие света на человеческий глаз (т. е. световое ощущение) весьма сильно зависит от λ. Чувствительность среднего (нормального) глаза к свету разной длины волны характеризуют кривой видности или кривой относительной спектральной чувствительности. Vλ Максимум чувствительности при 1, 0 ходится на зеленый участок ВИ, т. е. на λm = 550 нм. Для характеристики интенсив 0, 5 ности света с учетом его способности вызывать зрительное ощущение (с учетом Vλ) используют , где 400 500 λm 600 700 λ, нм световой поток: Φ = ωλ=dΦэ /dλ – распределение потока по длинам волн; Φ в [Лм].
Шкала электромагнитных излучений Раздел физики, занимающийся изучением природы света, а именно изучением закономерностей испускания, распространения и взаимодействия света с веществом, называется оптикой. • Кривая видности В видимом диапазоне действие света на человеческий глаз (т. е. световое ощущение) весьма сильно зависит от λ. Чувствительность среднего (нормального) глаза к свету разной длины волны характеризуют кривой видности или кривой относительной спектральной чувствительности. Vλ Максимум чувствительности при 1, 0 ходится на зеленый участок ВИ, т. е. на λm = 550 нм. Для характеристики интенсив 0, 5 ности света с учетом его способности вызывать зрительное ощущение (с учетом Vλ) используют , где 400 500 λm 600 700 λ, нм световой поток: Φ = ωλ=dΦэ /dλ – распределение потока по длинам волн; Φ в [Лм].
 Краткая историческая справка о развитии взглядов на природу света • Ньютоновская корпускулярная теория света В конце 17 в. И. Ньютоном было предложено рассматривать свет как поток частиц, испускаемых источником и распространяющихся в однородной среде прямолинейно. Отражение и преломление света эта теория объясняла механистически: отражение световой корпускулы от зеркала сравнивалось с отражением упругого шарика от стенки; преломление света объяснялось притяжением корпускулы при переходе из одной среды в другую частицами второй среды. При этом полагалось, что в двух средах тангенциальные составляющие скорости света сохранялись, т. е. v 1τ = v 2τ, а нормальные – изменялись. В связи с этим, так как v 1τ = v 1. sin α и v 2τ = v 2. sin β , то относительный показатель преломления этих сред (по определению n 21 = sin α / sin β) будет равен отношению скоростей корпускулы v 2 /v 1. В случае n 21 > 1 имеем v 2 > v 1, т. е. частица движется в более плотной среде быстрее, чем в менее плотной, что невероятно? ! Также ньютоновская теория света не смогла v 1 объяснить такие явления как интерференция, α 1 дифракция, поляризация (1817 г. ) и в 19 в. β уступила место волновой теории. v 2 2
Краткая историческая справка о развитии взглядов на природу света • Ньютоновская корпускулярная теория света В конце 17 в. И. Ньютоном было предложено рассматривать свет как поток частиц, испускаемых источником и распространяющихся в однородной среде прямолинейно. Отражение и преломление света эта теория объясняла механистически: отражение световой корпускулы от зеркала сравнивалось с отражением упругого шарика от стенки; преломление света объяснялось притяжением корпускулы при переходе из одной среды в другую частицами второй среды. При этом полагалось, что в двух средах тангенциальные составляющие скорости света сохранялись, т. е. v 1τ = v 2τ, а нормальные – изменялись. В связи с этим, так как v 1τ = v 1. sin α и v 2τ = v 2. sin β , то относительный показатель преломления этих сред (по определению n 21 = sin α / sin β) будет равен отношению скоростей корпускулы v 2 /v 1. В случае n 21 > 1 имеем v 2 > v 1, т. е. частица движется в более плотной среде быстрее, чем в менее плотной, что невероятно? ! Также ньютоновская теория света не смогла v 1 объяснить такие явления как интерференция, α 1 дифракция, поляризация (1817 г. ) и в 19 в. β уступила место волновой теории. v 2 2
 Краткая историческая справка о развитии взглядов на природу света • Волновая теория света Хр. Гюйгенса Волновая теория света, впервые выдвинутая голандцем Хр. Гюйгенсом в работе «Трактат о свете» (1690 г. ), рассматривала свет как упругий импульс, распространяющийся в «световом эфире» . Под «эфиром» понималась особая среда, заполняющая все пространство и пронизывающая вещество. Согласно Гюйгенсу свет – это упругие волны в «эфире» , подобные звуковым волнам в воздухе. Волновая теория хорошо объясняла явления интерференции и дифракции. Но, когда эксперименты по поляризации света указали на факт поперечности световых волн, представления о «механическом эфире» проявили свою несостоятельность. Как известно, поперечные волны упругости возможны лишь в твердом теле, а принимать эфир за твердое тело – абсурдно (тогда бы эфир оказывал бы воздействия на движущиеся в нем объекты).
Краткая историческая справка о развитии взглядов на природу света • Волновая теория света Хр. Гюйгенса Волновая теория света, впервые выдвинутая голандцем Хр. Гюйгенсом в работе «Трактат о свете» (1690 г. ), рассматривала свет как упругий импульс, распространяющийся в «световом эфире» . Под «эфиром» понималась особая среда, заполняющая все пространство и пронизывающая вещество. Согласно Гюйгенсу свет – это упругие волны в «эфире» , подобные звуковым волнам в воздухе. Волновая теория хорошо объясняла явления интерференции и дифракции. Но, когда эксперименты по поляризации света указали на факт поперечности световых волн, представления о «механическом эфире» проявили свою несостоятельность. Как известно, поперечные волны упругости возможны лишь в твердом теле, а принимать эфир за твердое тело – абсурдно (тогда бы эфир оказывал бы воздействия на движущиеся в нем объекты).
 Краткая историческая справка о развитии взглядов на природу света • Электромагнитная волновая природа света В 1865 г. Дж. Максвелл, создав замкнутую теорию э/м поля, показал, что переменные э/м поля распространяются в пространстве со скоростью света. Тем самым было установлено, что свет имеет электромагнитную природу и его можно рассматривать как э/м волну. Эта теория света позволила объяснить большой круг оптических явлений (интерференция, дифракция, поляризация, дисперсия). Однако на рубеже 19 -20 вв. она столкнулась с «непреодолимыми» препятствиями при попытках объяснить с классических (неквантовых) позиций такие явления как фотоэффект, комптоновское рассеяние рентгеновских фотонов на веществе и др. , где проявляются корпускулярные черты света.
Краткая историческая справка о развитии взглядов на природу света • Электромагнитная волновая природа света В 1865 г. Дж. Максвелл, создав замкнутую теорию э/м поля, показал, что переменные э/м поля распространяются в пространстве со скоростью света. Тем самым было установлено, что свет имеет электромагнитную природу и его можно рассматривать как э/м волну. Эта теория света позволила объяснить большой круг оптических явлений (интерференция, дифракция, поляризация, дисперсия). Однако на рубеже 19 -20 вв. она столкнулась с «непреодолимыми» препятствиями при попытках объяснить с классических (неквантовых) позиций такие явления как фотоэффект, комптоновское рассеяние рентгеновских фотонов на веществе и др. , где проявляются корпускулярные черты света.
 Краткая историческая справка о развитии взглядов на природу света • Дуализм природы света Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна (интерференция, дифракция, поляризация, дисперсия), в других случаях – как поток особых частиц (не обладающих массой покоя) – фотонов (фотоэффект, эффект Комптона). Синтез корпускулярных и волновых представлений о свете осуществляется в современной квантовой теории, которая рассматривает свет как поток фотонов, распространяющийся по законам электромагнитных волн.
Краткая историческая справка о развитии взглядов на природу света • Дуализм природы света Свет представляет собой сложное явление: в одних случаях он ведет себя как электромагнитная волна (интерференция, дифракция, поляризация, дисперсия), в других случаях – как поток особых частиц (не обладающих массой покоя) – фотонов (фотоэффект, эффект Комптона). Синтез корпускулярных и волновых представлений о свете осуществляется в современной квантовой теории, которая рассматривает свет как поток фотонов, распространяющийся по законам электромагнитных волн.
 Световая электромагнитная волна и ее характеристики • Световой вектор В основе волновой оптики (здесь изучаются интерференция, дифракция, поляризация, дисперсия) лежат фундаментальные уравнения Максвелла. В световой волне, как в э/м волне, колеблются векторы Е и Н по гармоническим законам: Как показывают многочисленные эксперименты физиологическое, фотохимическое, фотоэлектрическое и др. действия света вызываются, главным образом, колебаниями вектора электрического поля Е. В связи с этим в оптике обычно говорят о световом векторе, подразумевая под ним именно вектор Е. Изменения во времени и пространстве проекции светового вектора на направление его колебания будем задавать уравнением: E = Emcos(ωt – k. r + α 0) (1) где Еm (или А) – амплитуда колебаний светового вектора, ω – циклическая частота колебаний, k = 2π/λ – волновое число, r – расстояние от источника до рассматриваемой точки вдоль волны, α 0 – начальная фаза колебаний (часто обнуляется).
Световая электромагнитная волна и ее характеристики • Световой вектор В основе волновой оптики (здесь изучаются интерференция, дифракция, поляризация, дисперсия) лежат фундаментальные уравнения Максвелла. В световой волне, как в э/м волне, колеблются векторы Е и Н по гармоническим законам: Как показывают многочисленные эксперименты физиологическое, фотохимическое, фотоэлектрическое и др. действия света вызываются, главным образом, колебаниями вектора электрического поля Е. В связи с этим в оптике обычно говорят о световом векторе, подразумевая под ним именно вектор Е. Изменения во времени и пространстве проекции светового вектора на направление его колебания будем задавать уравнением: E = Emcos(ωt – k. r + α 0) (1) где Еm (или А) – амплитуда колебаний светового вектора, ω – циклическая частота колебаний, k = 2π/λ – волновое число, r – расстояние от источника до рассматриваемой точки вдоль волны, α 0 – начальная фаза колебаний (часто обнуляется).
 Световая электромагнитная волна и ее характеристики
Световая электромагнитная волна и ее характеристики
 Интенсивность световой волны Световую волну характеризуют также интенсивностью I – это модуль среднего по времени значения вектора плотности потока энергии (вектора Пойнтинга S): I = |
Интенсивность световой волны Световую волну характеризуют также интенсивностью I – это модуль среднего по времени значения вектора плотности потока энергии (вектора Пойнтинга S): I = || = |
 <Законы геометрической оптики> Пусть плоская э/м волна падает на плоскую границу раздела двух однородных прозрачных диэлектриков с показателями преломления n 1 и n 2. Волна в этом случае частично отражается от границы раздела, а частично преломляется и переходит во вторую среду. • Закон прямолинейного распространения света в однородной среде. • Закон отражения света: угол отражения α′ равен углу падения α. • Закон преломления света (закон Снеллиуса): отношение синуса угла падения α к синусу угла преломления β есть относительный показатель преломления второй среды к первой n 21 или отношение абсолютного показателя преломления второй среды к показателю первой среды, т. е. sin α / sin β = n 21 = n 2 / n 1 • Луч падающий, луч отраженный и луч преломленный лежат в одной плоскости с нормалью к точке падения луча. Общую плоскость называют плоскостью падения. n 1 αα n 2 β ′
<Законы геометрической оптики> Пусть плоская э/м волна падает на плоскую границу раздела двух однородных прозрачных диэлектриков с показателями преломления n 1 и n 2. Волна в этом случае частично отражается от границы раздела, а частично преломляется и переходит во вторую среду. • Закон прямолинейного распространения света в однородной среде. • Закон отражения света: угол отражения α′ равен углу падения α. • Закон преломления света (закон Снеллиуса): отношение синуса угла падения α к синусу угла преломления β есть относительный показатель преломления второй среды к первой n 21 или отношение абсолютного показателя преломления второй среды к показателю первой среды, т. е. sin α / sin β = n 21 = n 2 / n 1 • Луч падающий, луч отраженный и луч преломленный лежат в одной плоскости с нормалью к точке падения луча. Общую плоскость называют плоскостью падения. n 1 αα n 2 β ′
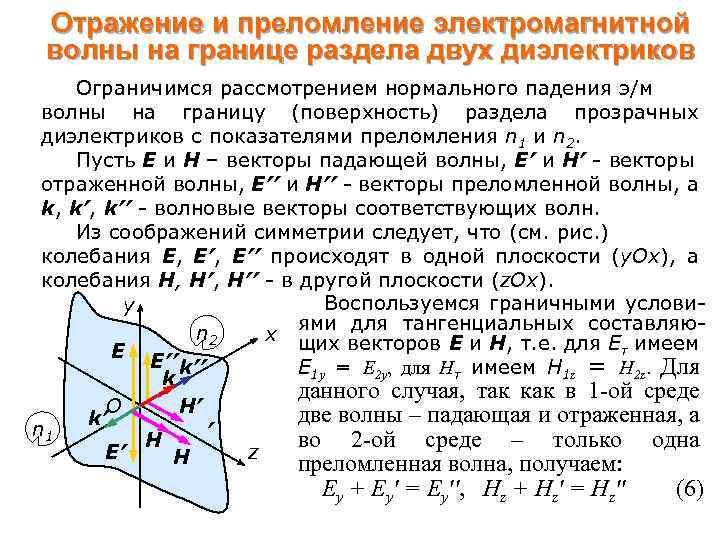 Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков Ограничимся рассмотрением нормального падения э/м волны на границу (поверхность) раздела прозрачных диэлектриков с показателями преломления n 1 и n 2. Пусть Е и Н – векторы падающей волны, Е′ и Н′ - векторы отраженной волны, Е′′ и Н′′ - векторы преломленной волны, а k, k′′ - волновые векторы соответствующих волн. Из соображений симметрии следует, что (см. рис. ) колебания Е, Е′′ происходят в одной плоскости (y. Ox), а колебания Н, Н′′ - в другой плоскости (z. Ox). Воспользуемся граничными условиy ями для тангенциальных составляюn 2 x щих векторов Е и Н, т. е. для Е имеем τ E E′′ Е 1 y = E 2 y, для Нτ имеем Н 1 z = H 2 z. Для k′′ k данного случая, так как в 1 -ой среде O H′ две волны – падающая и отраженная, а k′ n 1 ′ во 2 -ой среде – только одна H E′ z H ′ преломленная волна, получаем: Еy + Ey′ = Ey′′, Hz + Hz′ = Hz′′ (6)
Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков Ограничимся рассмотрением нормального падения э/м волны на границу (поверхность) раздела прозрачных диэлектриков с показателями преломления n 1 и n 2. Пусть Е и Н – векторы падающей волны, Е′ и Н′ - векторы отраженной волны, Е′′ и Н′′ - векторы преломленной волны, а k, k′′ - волновые векторы соответствующих волн. Из соображений симметрии следует, что (см. рис. ) колебания Е, Е′′ происходят в одной плоскости (y. Ox), а колебания Н, Н′′ - в другой плоскости (z. Ox). Воспользуемся граничными условиy ями для тангенциальных составляюn 2 x щих векторов Е и Н, т. е. для Е имеем τ E E′′ Е 1 y = E 2 y, для Нτ имеем Н 1 z = H 2 z. Для k′′ k данного случая, так как в 1 -ой среде O H′ две волны – падающая и отраженная, а k′ n 1 ′ во 2 -ой среде – только одна H E′ z H ′ преломленная волна, получаем: Еy + Ey′ = Ey′′, Hz + Hz′ = Hz′′ (6)
 Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков
Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков
 Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков • Коэффициенты отражения и пропускания В случае нормального падения световой волны на поверхность раздела сред коэффициент отражения по определению есть отношение интенсивности отраженной волны к интенсивности падающей волны, т. е. : ρ = I′/I, а с учетом того, что I ~ n. Em 2, имеем ρ=n 1. Em′ 2/(n 1. Em 2) и после подстановки отношения Em′/Emиз (8) получаем Коэффициент пропускания, по определению: (9) (10) Замечания. Коэффициенты отражения и пропускания должны подчиняться условию нормировки: ρ + τ = 1. В случае падения волны не по нормали к границе раздела коэффициент пропускания определяется как отношение потока энергии в прошедшей волне к потоку энергии в падающей волне, т. е. τ = Ф′′/Ф
Отражение и преломление электромагнитной волны на границе раздела двух диэлектриков • Коэффициенты отражения и пропускания В случае нормального падения световой волны на поверхность раздела сред коэффициент отражения по определению есть отношение интенсивности отраженной волны к интенсивности падающей волны, т. е. : ρ = I′/I, а с учетом того, что I ~ n. Em 2, имеем ρ=n 1. Em′ 2/(n 1. Em 2) и после подстановки отношения Em′/Emиз (8) получаем Коэффициент пропускания, по определению: (9) (10) Замечания. Коэффициенты отражения и пропускания должны подчиняться условию нормировки: ρ + τ = 1. В случае падения волны не по нормали к границе раздела коэффициент пропускания определяется как отношение потока энергии в прошедшей волне к потоку энергии в падающей волне, т. е. τ = Ф′′/Ф
 Интерференция света. Разность фаз и оптическая разность хода • Интерференционное уравнение Рассмотрим наложение (суперпозицию) двух гармонических световых волн одинаковой частоты ω, которые возбуждают в данной точке пространства колебания одинакового направления с амплитудами А 1 и А 2, т. е. A 1. cos(ωt + α 1) и A 2. cos(ωt + α 2). Результирующее колебание с амплитудой А можно определить по теореме косинусов: А 2 = А 12+ А 22+ 2, А 1. А 2. cos δ, где δ = α 2 – α 1 – разность фаз возбуждаемых волнами колебаний. А А 2 δ А 1 Когерентными волнами называются волны одинаковой частоты, колебания светового вектора в которых отличаются постоянством разности фаз (разность фаз не зависит от времени). Этому условию удовлетворяют полностью монохроматические волны одинаковой частоты.
Интерференция света. Разность фаз и оптическая разность хода • Интерференционное уравнение Рассмотрим наложение (суперпозицию) двух гармонических световых волн одинаковой частоты ω, которые возбуждают в данной точке пространства колебания одинакового направления с амплитудами А 1 и А 2, т. е. A 1. cos(ωt + α 1) и A 2. cos(ωt + α 2). Результирующее колебание с амплитудой А можно определить по теореме косинусов: А 2 = А 12+ А 22+ 2, А 1. А 2. cos δ, где δ = α 2 – α 1 – разность фаз возбуждаемых волнами колебаний. А А 2 δ А 1 Когерентными волнами называются волны одинаковой частоты, колебания светового вектора в которых отличаются постоянством разности фаз (разность фаз не зависит от времени). Этому условию удовлетворяют полностью монохроматические волны одинаковой частоты.
 Интерференция света. Разность фаз и оптическая разность хода • Интерференционное уравнение В случае некогерентных волн разность фаз δ как-то случайно непрерывно изменяется во времени, принимая с равной вероятностью любые значения; при этом среднее по времени значение
Интерференция света. Разность фаз и оптическая разность хода • Интерференционное уравнение В случае некогерентных волн разность фаз δ как-то случайно непрерывно изменяется во времени, принимая с равной вероятностью любые значения; при этом среднее по времени значение
 Интерференция света. Разность фаз и оптическая разность хода • Получение интерференционной картины от обычного источника света Естественный свет, обусловленный обычными некогерентными источниками (не лазерами) не является монохроматичным, так как представляет собой суперпозицию целого огромного множества элементарных цугов волн, испускаемых возбужденными атомами (независимо и случайным образом) излучающего тела; причем фазы колебаний отдельных цугов никак не урегулированы и меняются случайным образом. В связи с этим возникает трудность в получении интерференционной картины от двух (и более) обычных источников. Однако когерентные световые волны можно получить даже от обычных источников. Для этого волну, излучаемую одним источником (обычная лампа), разделяют оптическим способом (с помощью отражений и преломлений) на две части (два луча) и затем накладывают их друг на друга подходящим способом. «Расщепленные» лучи пройдут разные оптические пути ni. ri и будут обладать оптической разностью хода: Δ = n 2. r 2 – n 1. r 1 (11) При этом разность хода Δ не должна быть слишком большой, так как складывающиеся колебания должны принадлежать одному цугу волн
Интерференция света. Разность фаз и оптическая разность хода • Получение интерференционной картины от обычного источника света Естественный свет, обусловленный обычными некогерентными источниками (не лазерами) не является монохроматичным, так как представляет собой суперпозицию целого огромного множества элементарных цугов волн, испускаемых возбужденными атомами (независимо и случайным образом) излучающего тела; причем фазы колебаний отдельных цугов никак не урегулированы и меняются случайным образом. В связи с этим возникает трудность в получении интерференционной картины от двух (и более) обычных источников. Однако когерентные световые волны можно получить даже от обычных источников. Для этого волну, излучаемую одним источником (обычная лампа), разделяют оптическим способом (с помощью отражений и преломлений) на две части (два луча) и затем накладывают их друг на друга подходящим способом. «Расщепленные» лучи пройдут разные оптические пути ni. ri и будут обладать оптической разностью хода: Δ = n 2. r 2 – n 1. r 1 (11) При этом разность хода Δ не должна быть слишком большой, так как складывающиеся колебания должны принадлежать одному цугу волн
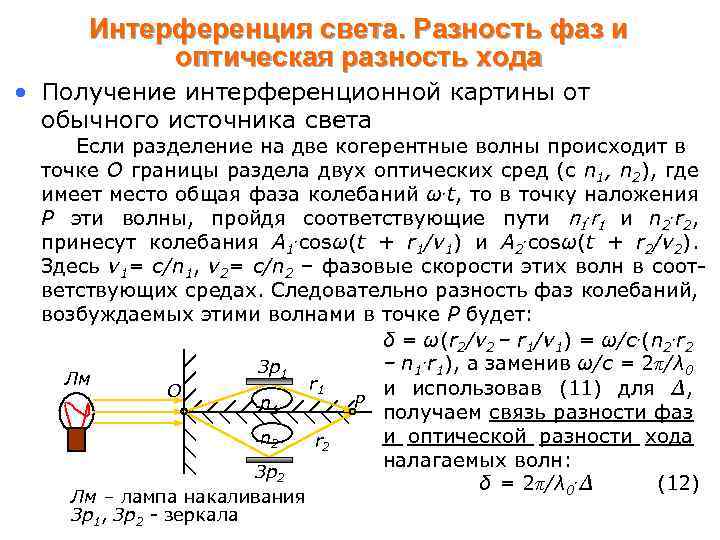 Интерференция света. Разность фаз и оптическая разность хода • Получение интерференционной картины от обычного источника света Если разделение на две когерентные волны происходит в точке О границы раздела двух оптических сред (с n 1, n 2), где имеет место общая фаза колебаний ω. t, то в точку наложения Р эти волны, пройдя соответствующие пути n 1. r 1 и n 2. r 2, принесут колебания A 1. cosω(t + r 1/v 1) и A 2. cosω(t + r 2/v 2). Здесь v 1= c/n 1, v 2= c/n 2 – фазовые скорости этих волн в соответствующих средах. Следовательно разность фаз колебаний, возбуждаемых этими волнами в точке Р будет: δ = ω(r 2/v 2 – r 1/v 1) = ω/c. (n 2. r 2 – n 1. r 1), а заменив ω/с = 2π/λ 0 Зр1 Лм r 1 и использовав (11) для Δ, O P n 1 получаем связь разности фаз и оптической разности хода n 2 r 2 налагаемых волн: Зр2 δ = 2π/λ 0. Δ (12) Лм – лампа накаливания Зр1, Зр2 - зеркала
Интерференция света. Разность фаз и оптическая разность хода • Получение интерференционной картины от обычного источника света Если разделение на две когерентные волны происходит в точке О границы раздела двух оптических сред (с n 1, n 2), где имеет место общая фаза колебаний ω. t, то в точку наложения Р эти волны, пройдя соответствующие пути n 1. r 1 и n 2. r 2, принесут колебания A 1. cosω(t + r 1/v 1) и A 2. cosω(t + r 2/v 2). Здесь v 1= c/n 1, v 2= c/n 2 – фазовые скорости этих волн в соответствующих средах. Следовательно разность фаз колебаний, возбуждаемых этими волнами в точке Р будет: δ = ω(r 2/v 2 – r 1/v 1) = ω/c. (n 2. r 2 – n 1. r 1), а заменив ω/с = 2π/λ 0 Зр1 Лм r 1 и использовав (11) для Δ, O P n 1 получаем связь разности фаз и оптической разности хода n 2 r 2 налагаемых волн: Зр2 δ = 2π/λ 0. Δ (12) Лм – лампа накаливания Зр1, Зр2 - зеркала
 Расчет интерференционной картины от двух когерентных источников • Методика расчета интерференционной картины Образовавшиеся после «расщепления» когерентные волны можно представить ( «как бы» ) исходящими из двух точечных источников S 1 и S 2 (действительных или мнимых – это не существенно), которые при условии Δ << 1 м - будут когерентными. В области, где эти волны перекрываются – в зоне интерференции – должна возникать интерференционная картина, т. е. система чередующихся максимумов и минимумов интенсивности освещенности, которую можно наблюдать на экране (в виде системы светлых и темных полос). Исследуем картину в точке Р экрана. 1) Если оптическая P r 1 разность хода лучей S 1 P и S 2 P S 1 равна целому числу длин волн: ЗИ r 2 Δmax= ±m. λ 0, где m=0, 1, 2, … (13) O 1 O то колебания в точке Р будут происходить в фазе (δ = ±m. 2π) S 2 Δ и условие (13) есть условие воз Э -никновения Imax.
Расчет интерференционной картины от двух когерентных источников • Методика расчета интерференционной картины Образовавшиеся после «расщепления» когерентные волны можно представить ( «как бы» ) исходящими из двух точечных источников S 1 и S 2 (действительных или мнимых – это не существенно), которые при условии Δ << 1 м - будут когерентными. В области, где эти волны перекрываются – в зоне интерференции – должна возникать интерференционная картина, т. е. система чередующихся максимумов и минимумов интенсивности освещенности, которую можно наблюдать на экране (в виде системы светлых и темных полос). Исследуем картину в точке Р экрана. 1) Если оптическая P r 1 разность хода лучей S 1 P и S 2 P S 1 равна целому числу длин волн: ЗИ r 2 Δmax= ±m. λ 0, где m=0, 1, 2, … (13) O 1 O то колебания в точке Р будут происходить в фазе (δ = ±m. 2π) S 2 Δ и условие (13) есть условие воз Э -никновения Imax.
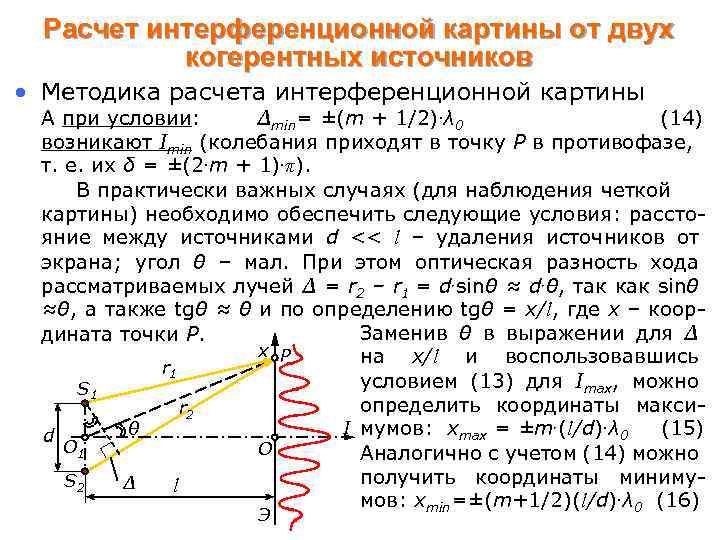 Расчет интерференционной картины от двух когерентных источников • Методика расчета интерференционной картины А при условии: Δmin= ±(m + 1/2). λ 0 (14) возникают Imin (колебания приходят в точку Р в противофазе, т. е. их δ = ±(2. m + 1). π). В практически важных случаях (для наблюдения четкой картины) необходимо обеспечить следующие условия: расстояние между источниками d << l – удаления источников от экрана; угол θ – мал. При этом оптическая разность хода рассматриваемых лучей Δ = r 2 – r 1 = d. sinθ ≈ d. θ, так как sinθ ≈θ, а также tgθ ≈ θ и по определению tgθ = x/l, где х – коор. Заменив θ в выражении для Δ дината точки Р. x P на x/l и воспользовавшись r 1 условием (13) для Imax, можно S 1 определить координаты максиr 2 I мумов: xmax = ±m. (l/d). λ 0 (15) θ d O 1 O Аналогично с учетом (14) можно получить координаты миниму. S 2 Δ l мов: xmin=±(m+1/2)(l/d). λ 0 (16) Э
Расчет интерференционной картины от двух когерентных источников • Методика расчета интерференционной картины А при условии: Δmin= ±(m + 1/2). λ 0 (14) возникают Imin (колебания приходят в точку Р в противофазе, т. е. их δ = ±(2. m + 1). π). В практически важных случаях (для наблюдения четкой картины) необходимо обеспечить следующие условия: расстояние между источниками d << l – удаления источников от экрана; угол θ – мал. При этом оптическая разность хода рассматриваемых лучей Δ = r 2 – r 1 = d. sinθ ≈ d. θ, так как sinθ ≈θ, а также tgθ ≈ θ и по определению tgθ = x/l, где х – коор. Заменив θ в выражении для Δ дината точки Р. x P на x/l и воспользовавшись r 1 условием (13) для Imax, можно S 1 определить координаты максиr 2 I мумов: xmax = ±m. (l/d). λ 0 (15) θ d O 1 O Аналогично с учетом (14) можно получить координаты миниму. S 2 Δ l мов: xmin=±(m+1/2)(l/d). λ 0 (16) Э
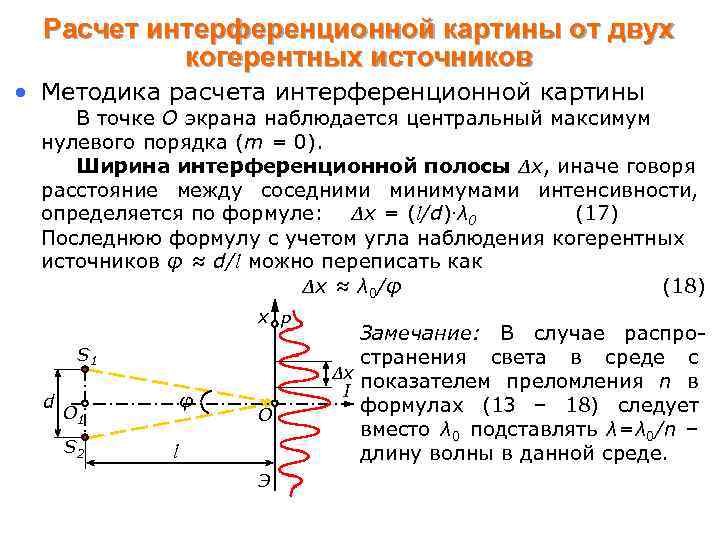 Расчет интерференционной картины от двух когерентных источников • Методика расчета интерференционной картины В точке О экрана наблюдается центральный максимум нулевого порядка (m = 0). Ширина интерференционной полосы Δх, иначе говоря расстояние между соседними минимумами интенсивности, определяется по формуле: Δх = (l/d). λ 0 (17) Последнюю формулу с учетом угла наблюдения когерентных источников φ ≈ d/l можно переписать как Δх ≈ λ 0/φ (18) x P S 1 d φ O 1 S 2 O l Э Замечание: В случае распространения света в среде с Δx показателем преломления n в I формулах (13 – 18) следует вместо λ 0 подставлять λ=λ 0/n – длину волны в данной среде.
Расчет интерференционной картины от двух когерентных источников • Методика расчета интерференционной картины В точке О экрана наблюдается центральный максимум нулевого порядка (m = 0). Ширина интерференционной полосы Δх, иначе говоря расстояние между соседними минимумами интенсивности, определяется по формуле: Δх = (l/d). λ 0 (17) Последнюю формулу с учетом угла наблюдения когерентных источников φ ≈ d/l можно переписать как Δх ≈ λ 0/φ (18) x P S 1 d φ O 1 S 2 O l Э Замечание: В случае распространения света в среде с Δx показателем преломления n в I формулах (13 – 18) следует вместо λ 0 подставлять λ=λ 0/n – длину волны в данной среде.
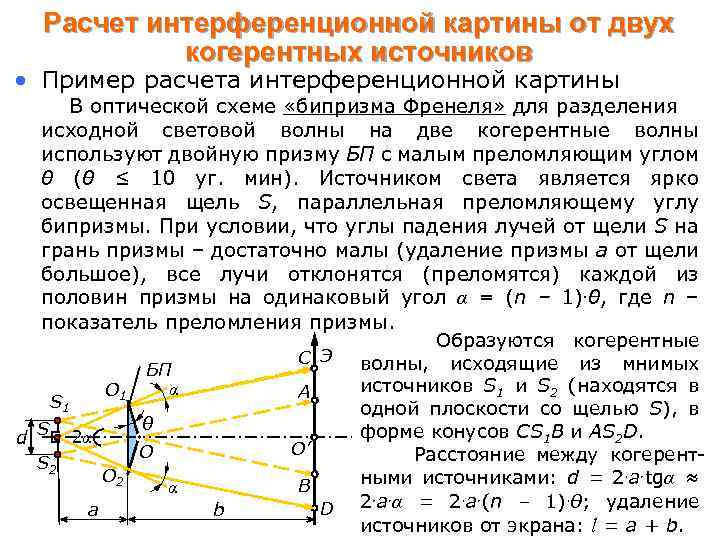 Расчет интерференционной картины от двух когерентных источников • Пример расчета интерференционной картины В оптической схеме «бипризма Френеля» для разделения исходной световой волны на две когерентные волны используют двойную призму БП с малым преломляющим углом θ (θ ≤ 10 уг. мин). Источником света является ярко освещенная щель S, параллельная преломляющему углу бипризмы. При условии, что углы падения лучей от щели S на грань призмы – достаточно малы (удаление призмы а от щели большое), все лучи отклонятся (преломятся) каждой из половин призмы на одинаковый угол α = (n – 1). θ, где n – показатель преломления призмы. Образуются когерентные O 1 S 1 d S 2α S 2 a С Э БП α A θ O’ O O 2 В α b D волны, исходящие из мнимых источников S 1 и S 2 (находятся в одной плоскости со щелью S), в форме конусов CS 1 B и AS 2 D. Расстояние между когерентными источниками: d = 2. a. tgα ≈ 2. a. α = 2. a. (n – 1). θ; удаление источников от экрана: l = a + b.
Расчет интерференционной картины от двух когерентных источников • Пример расчета интерференционной картины В оптической схеме «бипризма Френеля» для разделения исходной световой волны на две когерентные волны используют двойную призму БП с малым преломляющим углом θ (θ ≤ 10 уг. мин). Источником света является ярко освещенная щель S, параллельная преломляющему углу бипризмы. При условии, что углы падения лучей от щели S на грань призмы – достаточно малы (удаление призмы а от щели большое), все лучи отклонятся (преломятся) каждой из половин призмы на одинаковый угол α = (n – 1). θ, где n – показатель преломления призмы. Образуются когерентные O 1 S 1 d S 2α S 2 a С Э БП α A θ O’ O O 2 В α b D волны, исходящие из мнимых источников S 1 и S 2 (находятся в одной плоскости со щелью S), в форме конусов CS 1 B и AS 2 D. Расстояние между когерентными источниками: d = 2. a. tgα ≈ 2. a. α = 2. a. (n – 1). θ; удаление источников от экрана: l = a + b.
 Расчет интерференционной картины от двух когерентных источников • Пример расчета интерференционной картины В результате наложения когерентных волн в пространстве за бипризмой формируется зона интерференции ЗИ, которая образует на экране Э интерференционную картину шириной: АВ = 2. b. tgα ≈ 2. b. α = 2. b. (n – 1). θ Используя стандартную формулу (17), определяем ширину интерференционной полосы: Δx = (l/d). λ = Полное число наблюдаемых полос в картине определяется как: O 1 S 1 d S 2α S 2 a θ A ЗИ 2α O O 2 С Э БП α O’ В α b D
Расчет интерференционной картины от двух когерентных источников • Пример расчета интерференционной картины В результате наложения когерентных волн в пространстве за бипризмой формируется зона интерференции ЗИ, которая образует на экране Э интерференционную картину шириной: АВ = 2. b. tgα ≈ 2. b. α = 2. b. (n – 1). θ Используя стандартную формулу (17), определяем ширину интерференционной полосы: Δx = (l/d). λ = Полное число наблюдаемых полос в картине определяется как: O 1 S 1 d S 2α S 2 a θ A ЗИ 2α O O 2 С Э БП α O’ В α b D
 Взаимная когерентность световых волн Принято называть когерентностью согласованное протекание нескольких колебательных или волновых процессов. Различают: временную и пространственную когерентность. Степень согласованности колебательных (волновых) процессов называют степенью когерентности. Так как в общем случае реальные световые волны не являются ни строго когерентными (когда у них разность фаз δ= const во времени), ни строго некогерентными (когда δ –var хаотически во времени), они – частично когерентны (для них -1< cosδ < 1), то при суперпозиции двух таких волн наблюдаются максимумы и минимумы интенсивности, которые зависят от времени: где |γ 12(τ)| - степень взаимной когерентности двух волн; причем при |γ 12(τ)| = 1 имеем полностью когерентные волны, при |γ 12(τ)| = 0 – полностью некогерентные волны и при 0<|γ 12(τ)|<1 – частично когерентные волны.
Взаимная когерентность световых волн Принято называть когерентностью согласованное протекание нескольких колебательных или волновых процессов. Различают: временную и пространственную когерентность. Степень согласованности колебательных (волновых) процессов называют степенью когерентности. Так как в общем случае реальные световые волны не являются ни строго когерентными (когда у них разность фаз δ= const во времени), ни строго некогерентными (когда δ –var хаотически во времени), они – частично когерентны (для них -1< cosδ < 1), то при суперпозиции двух таких волн наблюдаются максимумы и минимумы интенсивности, которые зависят от времени: где |γ 12(τ)| - степень взаимной когерентности двух волн; причем при |γ 12(τ)| = 1 имеем полностью когерентные волны, при |γ 12(τ)| = 0 – полностью некогерентные волны и при 0<|γ 12(τ)|<1 – частично когерентные волны.
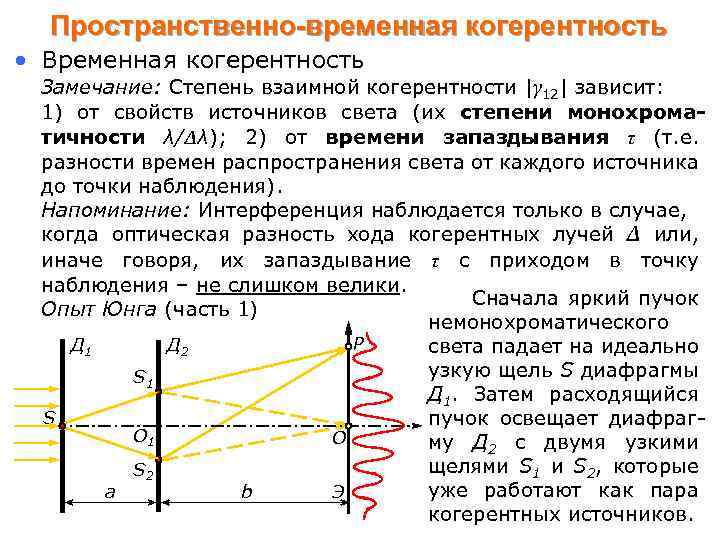 Пространственно-временная когерентность • Временная когерентность Замечание: Степень взаимной когерентности |γ 12| зависит: 1) от свойств источников света (их степени монохроматичности λ/Δλ); 2) от времени запаздывания τ (т. е. разности времен распространения света от каждого источника до точки наблюдения). Напоминание: Интерференция наблюдается только в случае, когда оптическая разность хода когерентных лучей Δ или, иначе говоря, их запаздывание τ с приходом в точку наблюдения – не слишком велики. Сначала яркий пучок Опыт Юнга (часть 1) немонохроматического P Д 1 Д 2 света падает на идеально узкую щель S диафрагмы S 1 Д 1. Затем расходящийся S пучок освещает диафраг. O 1 O му Д 2 с двумя узкими щелями S 1 и S 2, которые S 2 уже работают как пара a b Э когерентных источников.
Пространственно-временная когерентность • Временная когерентность Замечание: Степень взаимной когерентности |γ 12| зависит: 1) от свойств источников света (их степени монохроматичности λ/Δλ); 2) от времени запаздывания τ (т. е. разности времен распространения света от каждого источника до точки наблюдения). Напоминание: Интерференция наблюдается только в случае, когда оптическая разность хода когерентных лучей Δ или, иначе говоря, их запаздывание τ с приходом в точку наблюдения – не слишком велики. Сначала яркий пучок Опыт Юнга (часть 1) немонохроматического P Д 1 Д 2 света падает на идеально узкую щель S диафрагмы S 1 Д 1. Затем расходящийся S пучок освещает диафраг. O 1 O му Д 2 с двумя узкими щелями S 1 и S 2, которые S 2 уже работают как пара a b Э когерентных источников.
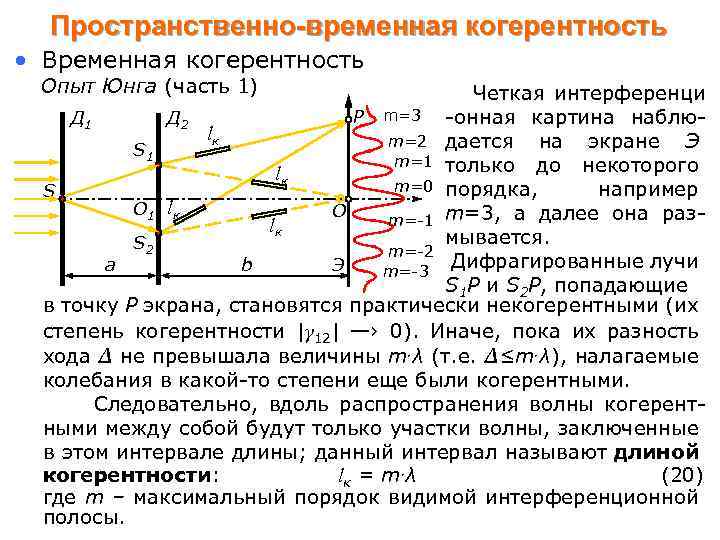 Пространственно-временная когерентность • Временная когерентность Опыт Юнга (часть 1) Четкая интерференци P m=3 -онная картина наблю. Д 1 Д 2 lк m=2 дается на экране Э S 1 m=1 только до некоторого lк m=0 порядка, например S O 1 l к O m=-1 m=3, а далее она разlк мывается. S 2 m=-2 Дифрагированные лучи a b Э m=-3 S 1 Р и S 2 Р, попадающие в точку Р экрана, становятся практически некогерентными (их степень когерентности |γ 12| —› 0). Иначе, пока их разность хода Δ не превышала величины m. λ (т. е. Δ≤m. λ), налагаемые колебания в какой-то степени еще были когерентными. Следовательно, вдоль распространения волны когерентными между собой будут только участки волны, заключенные в этом интервале длины; данный интервал называют длиной когерентности: lк = m. λ (20) где m – максимальный порядок видимой интерференционной полосы.
Пространственно-временная когерентность • Временная когерентность Опыт Юнга (часть 1) Четкая интерференци P m=3 -онная картина наблю. Д 1 Д 2 lк m=2 дается на экране Э S 1 m=1 только до некоторого lк m=0 порядка, например S O 1 l к O m=-1 m=3, а далее она разlк мывается. S 2 m=-2 Дифрагированные лучи a b Э m=-3 S 1 Р и S 2 Р, попадающие в точку Р экрана, становятся практически некогерентными (их степень когерентности |γ 12| —› 0). Иначе, пока их разность хода Δ не превышала величины m. λ (т. е. Δ≤m. λ), налагаемые колебания в какой-то степени еще были когерентными. Следовательно, вдоль распространения волны когерентными между собой будут только участки волны, заключенные в этом интервале длины; данный интервал называют длиной когерентности: lк = m. λ (20) где m – максимальный порядок видимой интерференционной полосы.
 Пространственно-временная когерентность • Временная когерентность Опыт Юнга (часть 1) Выходящие из щелей лучи S 1 P и S 2 P – изначально когерентны и обладают длиной когерентности lк, но по мере их распространения к точке Р и далее, у них растет разность хода Δ (по сравнению с лучами, попадающими в центральную область экрана), их участки когерентности постепенно сдвигаются относительно друга и, начиная с точки Р, перестают перекрывать друга. В результате здесь накладываются уже некогерентные колебания, и интерференционные полосы исчезают. Часто используют понятие временной когерентности, которой характеризуют сохранение взаимной когерентности при временном запаздывании двух волн, полученных от одного источника (или от одной точки волнового поля). Количественной характеристикой здесь служит время когерентности τк – это минимальное запаздывание τ, для которого степень взаимной когерентности |γ 12(τ)| = 0. Связь длины когерентности и времени когерентности (для вакуума): lк = τк. c (21)
Пространственно-временная когерентность • Временная когерентность Опыт Юнга (часть 1) Выходящие из щелей лучи S 1 P и S 2 P – изначально когерентны и обладают длиной когерентности lк, но по мере их распространения к точке Р и далее, у них растет разность хода Δ (по сравнению с лучами, попадающими в центральную область экрана), их участки когерентности постепенно сдвигаются относительно друга и, начиная с точки Р, перестают перекрывать друга. В результате здесь накладываются уже некогерентные колебания, и интерференционные полосы исчезают. Часто используют понятие временной когерентности, которой характеризуют сохранение взаимной когерентности при временном запаздывании двух волн, полученных от одного источника (или от одной точки волнового поля). Количественной характеристикой здесь служит время когерентности τк – это минимальное запаздывание τ, для которого степень взаимной когерентности |γ 12(τ)| = 0. Связь длины когерентности и времени когерентности (для вакуума): lк = τк. c (21)
 Пространственно-временная когерентность • Временная когерентность Так как реальные источники – не монохроматичны, их свет – это набор монохроматических компонент в некотором конечном интервале длин волн [λ, λ+Δλ] (предполагается равномерное распределение компонент по интервалу), а ширина интерференционных полос Δх ~ λ, то у световой волны наряду с основными максимумами Imax, обусловленными действием крайних составляющих λ и (λ+Δλ), начинают сказываться (особенно с некоторого m=3) дополнительные максимумы, вызванные промежуточными спектральными компонентами λi. Эти максимумы постепенно будут заполнять промежутки между основными Imax, а этот процесс приведет к «смазыванию» интерференционной картины полос. Таким образом, условием исчезновения четких полос является равенство: m. (λ+Δλ) = (m+1). λ, где m – максимальный наблюдаемый порядок в картине; при этом Imax m-го порядка от длины волны (λ+Δλ) наложится на Imax (m+1)-го порядка от длины λ. Разрешив последнее равенство относительно порядка m = λ/Δλ, где справа стоит степень монохроматичности источника, согласно (20) получим lк = m. λ = λ 2/Δλ (22)
Пространственно-временная когерентность • Временная когерентность Так как реальные источники – не монохроматичны, их свет – это набор монохроматических компонент в некотором конечном интервале длин волн [λ, λ+Δλ] (предполагается равномерное распределение компонент по интервалу), а ширина интерференционных полос Δх ~ λ, то у световой волны наряду с основными максимумами Imax, обусловленными действием крайних составляющих λ и (λ+Δλ), начинают сказываться (особенно с некоторого m=3) дополнительные максимумы, вызванные промежуточными спектральными компонентами λi. Эти максимумы постепенно будут заполнять промежутки между основными Imax, а этот процесс приведет к «смазыванию» интерференционной картины полос. Таким образом, условием исчезновения четких полос является равенство: m. (λ+Δλ) = (m+1). λ, где m – максимальный наблюдаемый порядок в картине; при этом Imax m-го порядка от длины волны (λ+Δλ) наложится на Imax (m+1)-го порядка от длины λ. Разрешив последнее равенство относительно порядка m = λ/Δλ, где справа стоит степень монохроматичности источника, согласно (20) получим lк = m. λ = λ 2/Δλ (22)
 Пространственно-временная когерентность • Пространственная когерентность Пространственной когерентностью пучка световых лучей характеризуют наличие взаимной когерентности двух лучей, взятых из различных точек сечения пучка. При этом взаимная когерентность проверяется по интерференции при запаздывании τ = 0, т. е. в системе (19) для Imax и Imin используется степень взаимной когерентности |γ 12(0)|. Количественной характеристикой пространственной когерентности может служить площадь когерентности Sк – это ограниченная кривой |γ 12(0)| = 0 площадь нормального сечения пучка лучей, в пределах которой степень когерентности принимает значения от 1 (внутри сечения) до 0 (на границе сечения). Замечания: Так как строго монохроматический пучок лучей, испускаемых точеч. Sк ным источником, всегда когерентен, то он имеет неограниченную площадь Sк —›∞. γ 12(0)=1 γ 12(0)=0 С увеличением размеров реального источника площадь когерентности сужается.
Пространственно-временная когерентность • Пространственная когерентность Пространственной когерентностью пучка световых лучей характеризуют наличие взаимной когерентности двух лучей, взятых из различных точек сечения пучка. При этом взаимная когерентность проверяется по интерференции при запаздывании τ = 0, т. е. в системе (19) для Imax и Imin используется степень взаимной когерентности |γ 12(0)|. Количественной характеристикой пространственной когерентности может служить площадь когерентности Sк – это ограниченная кривой |γ 12(0)| = 0 площадь нормального сечения пучка лучей, в пределах которой степень когерентности принимает значения от 1 (внутри сечения) до 0 (на границе сечения). Замечания: Так как строго монохроматический пучок лучей, испускаемых точеч. Sк ным источником, всегда когерентен, то он имеет неограниченную площадь Sк —›∞. γ 12(0)=1 γ 12(0)=0 С увеличением размеров реального источника площадь когерентности сужается.
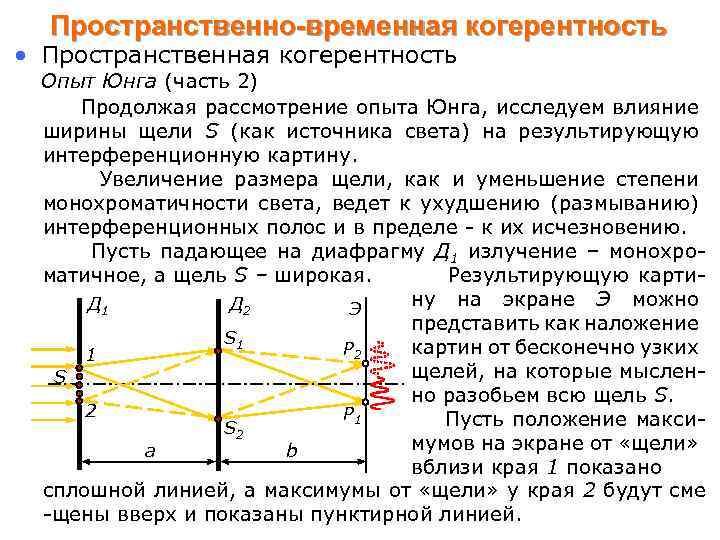 Пространственно-временная когерентность • Пространственная когерентность Опыт Юнга (часть 2) Продолжая рассмотрение опыта Юнга, исследуем влияние ширины щели S (как источника света) на результирующую интерференционную картину. Увеличение размера щели, как и уменьшение степени монохроматичности света, ведет к ухудшению (размыванию) интерференционных полос и в пределе - к их исчезновению. Пусть падающее на диафрагму Д 1 излучение – монохро Результирующую картиматичное, а щель S – широкая. ну на экране Э можно Д 1 Д 2 Э представить как наложение S 1 картин от бесконечно узких P 2 1 щелей, на которые мыслен. S но разобьем всю щель S. 2 P 1 Пусть положение макси. S 2 мумов на экране от «щели» a b вблизи края 1 показано сплошной линией, а максимумы от «щели» у края 2 будут сме -щены вверх и показаны пунктирной линией.
Пространственно-временная когерентность • Пространственная когерентность Опыт Юнга (часть 2) Продолжая рассмотрение опыта Юнга, исследуем влияние ширины щели S (как источника света) на результирующую интерференционную картину. Увеличение размера щели, как и уменьшение степени монохроматичности света, ведет к ухудшению (размыванию) интерференционных полос и в пределе - к их исчезновению. Пусть падающее на диафрагму Д 1 излучение – монохро Результирующую картиматичное, а щель S – широкая. ну на экране Э можно Д 1 Д 2 Э представить как наложение S 1 картин от бесконечно узких P 2 1 щелей, на которые мыслен. S но разобьем всю щель S. 2 P 1 Пусть положение макси. S 2 мумов на экране от «щели» a b вблизи края 1 показано сплошной линией, а максимумы от «щели» у края 2 будут сме -щены вверх и показаны пунктирной линией.
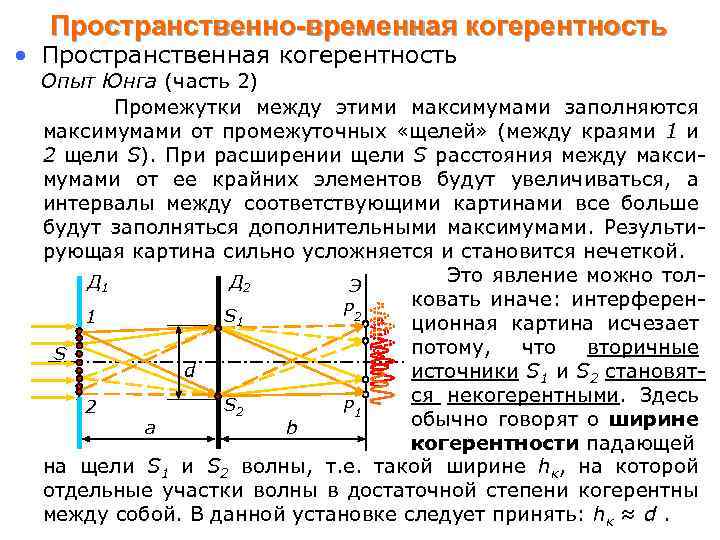 Пространственно-временная когерентность • Пространственная когерентность Опыт Юнга (часть 2) Промежутки между этими максимумами заполняются максимумами от промежуточных «щелей» (между краями 1 и 2 щели S). При расширении щели S расстояния между максимумами от ее крайних элементов будут увеличиваться, а интервалы между соответствующими картинами все больше будут заполняться дополнительными максимумами. Результирующая картина сильно усложняется и становится нечеткой. Это явление можно тол. Д 1 Д 2 Э ковать иначе: интерферен. P 2 S 1 1 ционная картина исчезает потому, что вторичные S d источники S 1 и S 2 становятся некогерентными. Здесь S 2 2 P 1 обычно говорят о ширине a b когерентности падающей на щели S 1 и S 2 волны, т. е. такой ширине hк, на которой отдельные участки волны в достаточной степени когерентны между собой. В данной установке следует принять: hк ≈ d.
Пространственно-временная когерентность • Пространственная когерентность Опыт Юнга (часть 2) Промежутки между этими максимумами заполняются максимумами от промежуточных «щелей» (между краями 1 и 2 щели S). При расширении щели S расстояния между максимумами от ее крайних элементов будут увеличиваться, а интервалы между соответствующими картинами все больше будут заполняться дополнительными максимумами. Результирующая картина сильно усложняется и становится нечеткой. Это явление можно тол. Д 1 Д 2 Э ковать иначе: интерферен. P 2 S 1 1 ционная картина исчезает потому, что вторичные S d источники S 1 и S 2 становятся некогерентными. Здесь S 2 2 P 1 обычно говорят о ширине a b когерентности падающей на щели S 1 и S 2 волны, т. е. такой ширине hк, на которой отдельные участки волны в достаточной степени когерентны между собой. В данной установке следует принять: hк ≈ d.
 Пространственно-временная когерентность • Пространственная когерентность Опыт Юнга (часть 2) В случае a = b и ширине щели S, равной ширине интерференционной полосы ∆х, интервал между максимумами от края 1 щели будет целиком заполнен максимумами от ее остальных элементов, и интерференционные полосы исчезнут. А так как ∆х = l/d. λ, то из последних равенств и условий следует: hког ≈ d = λ. l /∆x = λ. l /S = λ/(S/l) = λ/φ, где φ – угловая ширина щели S относительно диафрагмы со щелями (S 1, S 2). Общие выводы Д 1 Д 2 Для получения устойчивой четкой интерференционной карти. S 1 1 ны с использованием обычных S φ источников света необходимо: 1) исходную волну расщепить подd 2 ходящим способом на две части S 2 l (a) (луча), которые затем в области перекрытия дадут систему полос, но лишь при условиях: 2) lког > ∆; hког > d. Замечание. В расчетах обычно закладывают: lког ≥ 2. ∆; hког ≥ 2. d.
Пространственно-временная когерентность • Пространственная когерентность Опыт Юнга (часть 2) В случае a = b и ширине щели S, равной ширине интерференционной полосы ∆х, интервал между максимумами от края 1 щели будет целиком заполнен максимумами от ее остальных элементов, и интерференционные полосы исчезнут. А так как ∆х = l/d. λ, то из последних равенств и условий следует: hког ≈ d = λ. l /∆x = λ. l /S = λ/(S/l) = λ/φ, где φ – угловая ширина щели S относительно диафрагмы со щелями (S 1, S 2). Общие выводы Д 1 Д 2 Для получения устойчивой четкой интерференционной карти. S 1 1 ны с использованием обычных S φ источников света необходимо: 1) исходную волну расщепить подd 2 ходящим способом на две части S 2 l (a) (луча), которые затем в области перекрытия дадут систему полос, но лишь при условиях: 2) lког > ∆; hког > d. Замечание. В расчетах обычно закладывают: lког ≥ 2. ∆; hког ≥ 2. d.


