Лекции 13 14 и 15 Выполнил студент группы

Лекции 13, 14 и 15. Выполнил студент группы 103 Романов Владимир

Лекция 13

Введение Под дифракцией обычно понимают явление огибания волнами препятствий. В частности, свет может проникать в область геометрической тени за непрозрачными объектами на пути его распространения. При этом за препятствием, наблюдается чередование максимумов и минимумов освещённости, как и при интерференции когерентных световых пучков. Это позволяет сделать вывод о том, что природа явлений дифракции и интерференции одна и та же. Дифракция проявляет себя и в тех случаях, когда форма фронта воны нарушается прозрачными телами с оптическими характеристиками, отличными от остальной среды. Таким образом, в широком смысле дифракцией света можно назвать любое отклонение от законов геометрической оптики при распространении света в среде с резкими оптическими неоднородностями. Наше дальнейшее рассмотрение дифракции состоит в расчёте распределения освещённости в пространстве за препятствием определенных размеров и формы. Основой методологии решения этой задачи, а также понимания дифракционных явлений служит принцип Гюйгенса-Френеля, сформулированный в законченной форме в первой четверти XIX в.

Принцип Гюйгенса - Френеля: основной постулат волновой теории, описывающий и объясняющий механизм распространения волн, в частности, световых. Согласно принципу Гюйгенса - Френеля, световая волна, возбуждаемая какимлибо источником S, может быть представлена как результат суперпозиции когерентных вторичных волн, «излучаемых» фиктивными источниками. Такими источниками могут служить бесконечно малые элементы любой замкнутой поверхности, охватывающей источник S. Обычно в качестве этой поверхности выбирают одну из волновых поверхностей, поэтому все фиктивные источники действуют синфазно. Таким образом, волны, распространяющиеся от источника, являются результатом интерференции всех когерентных вторичных волн. Френель исключил возможность возникновения обратных вторичных волн и предположил, что если между источником и точкой наблюдения находится непрозрачный экран с отверстием, то на поверхности экрана амплитуда вторичных волн равна нулю, а в отверстии - такая же, как при отсутствии экрана.

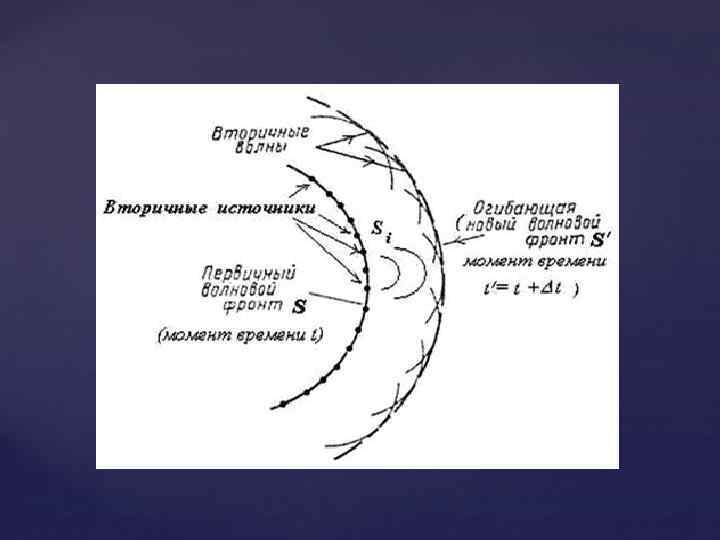
Метод зон Френеля Если источник света точечный, а среда однородная и изотропная, то волновые поверхности имеют сферическую форму. Выберем в качестве поверхности, фигурирующей в принципе Гюйгенса – Френеля, одну из них и будем считать её непрерывно заполненной когерентными вторичными источниками. Френель предложил для каждой точки наблюдения разбивать эту поверхность на отдельные участки – их называют зонами Френеля с таким расчётом, чтобы колебания, приходящие от двух соседних зон, при сложении гасили друга.

Чтобы произошло гашение колебаний, расстояния от соседних зон до точки наблюдения должны отличаться друг от друга на половину длины волны – такая разность хода обеспечит противоположность фаз колебаний, приходящих в точку наблюдения от этих зон. Поскольку величина амплитуды суммарного колебания в точке наблюдения в основном определяется площадью участка вспомогательной поверхности, то полное гашение колебаний, приходящих в точку наблюдения от двух соседних зон, происходит, если зоны имеют одинаковую площадь.

Дифракция Фринеля на круглом отверстии Дифракция Френеля — это дифракционная картина, которая наблюдается на небольшом расстоянии от препятствия, при условии, что основной вклад в интерференционную картину дают границы экрана.

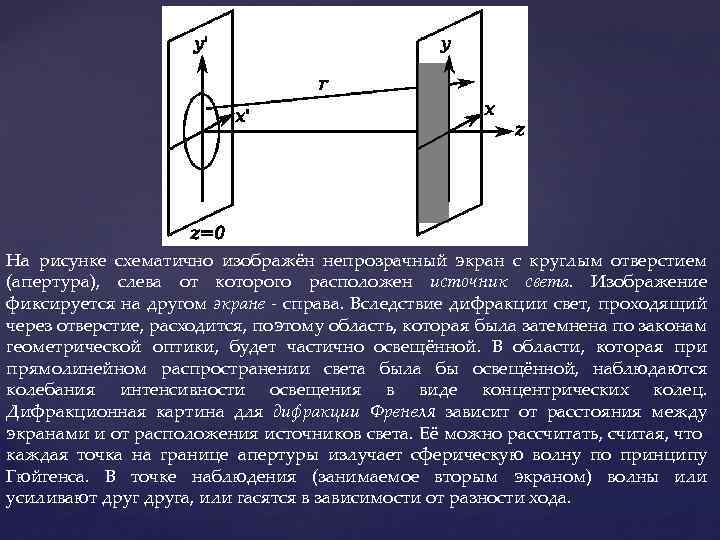На рисунке схематично изображён непрозрачный экран с круглым отверстием (апертура), слева от которого расположен источник света. Изображение фиксируется на другом экране - справа. Вследствие дифракции свет, проходящий через отверстие, расходится, поэтому область, которая была затемнена по законам геометрической оптики, будет частично освещённой. В области, которая при прямолинейном распространении света была бы освещённой, наблюдаются колебания интенсивности освещения в виде концентрических колец. Дифракционная картина для дифракции Френеля зависит от расстояния между экранами и от расположения источников света. Её можно рассчитать, считая, что каждая точка на границе апертуры излучает сферическую волну по принципу Гюйгенса. В точке наблюдения (занимаемое вторым экраном) волны или усиливают друга, или гасятся в зависимости от разности хода.

Дифракция Фраунгофера на одной щели Дифракция Фраунгофера — случай дифракции, при котором дифракционная картина наблюдается на значительном расстоянии от отверстия или преграды. Расстояние должно быть таким, чтобы можно было пренебречь в выражении для разности фаз членами порядка , что сильно упрощает теоретическое рассмотрение явления. Здесь z— расстояние от отверстия или преграды до плоскости наблюдения, λ— длина волны излучения, а p — радиальная координата рассматриваемой точки в плоскости наблюдения в полярной системе координат. Иными словами, дифракция Фраунгофера наблюдается тогда, когда число зон Френеля F<<1 , при этом приходящие в точку волны являются практически плоскими. При наблюдении данного вида дифракции изображение объекта не искажается и меняет только размер и положение в пространстве. В противоположность этому, при дифракции Френеля изображение меняет также свою форму и существенно искажается.

Дифракционная решётка — оптический прибор, работающий по принципу дифракции света, представляет собой совокупность большого числа регулярно расположенных штрихов (щелей, выступов), нанесённых на некоторую поверхность. Первое описание явления сделал Джеймс Грегори, который использовал в качестве решётки птичьи перья. Очень большая отражательная дифракционная решётка.

Виды решёток: • Отражательные: Штрихи нанесены на зеркальную (металлическую) поверхность, и наблюдение ведется в отражённом свете • Прозрачные: Штрихи нанесены на прозрачную поверхность (или вырезаются в виде щелей на непрозрачном экране), наблюдение ведется в проходящем свете. Описание явления: Фронт световой волны разбивается штрихами решётки на отдельные пучки когерентного света. Эти пучки претерпевают дифракцию на штрихах и интерферируют друг с другом. Так как для разных длин волн максимумы интерференции оказываются под разными углами (определяемыми разностью хода интерферирующих лучей), то белый свет раскладывается в спектр. Так выглядит свет лампы накаливания фонарика, прошедший через прозрачную дифракционную решётку. Нулевой максимум (m=0) соответствует свету, прошедшему сквозь решётку без отклонений. В силу дисперсии решётки в первом (m=± 1) максимуме можно наблюдать разложение света в спектр. Угол отклонения возрастает с ростом длины волны (от фиолетового цвета к красному).

Формулы Расстояние, через которое повторяются штрихи на решётке, называют периодом дифракционной решётки. Обозначают буквой d. Если известно число штрихов (N), приходящихся на 1 мм решётки, то период решётки находят по формуле: d=1/N мм. Условия интерференционных максимумов дифракционной решётки, наблюдаемых под определёнными углами, имеют вид: где d— период решётки, α— угол максимума данного цвета, k— порядок максимума, то есть порядковый номер максимума, отсчитанный от центра картинки, λ— длина волны. Если же свет падает на решётку под углом θ, то:

Изготовление Хорошие решётки требуют очень высокой точности изготовления. Если хоть одна щель из множества будет нанесена с ошибкой, то решётка будет бракована. Машина для изготовления решёток прочно и глубоко встраивается в специальный фундамент. Перед началом непосредственного изготовления решёток, машина работает 5 -20 часов на холостом ходу для стабилизации всех своих узлов. Нарезание решётки длится до 7 суток, хотя время нанесения штриха составляет 2 -3 секунды. Нарезка компакт-диска может считаться дифракционной решёткой.

Применение Дифракционную решётку применяют в спектральных приборах, также в качестве оптических датчиков линейных и угловых перемещений (измерительные дифракционные решётки), поляризаторов и фильтров инфракрасного излучения, делителей пучков в интерферометрах и так называемых «антибликовых» очках. Это дифракционная решетка, которая уменьшает длинну волны лазера с фемтосекундного диапазона в наносекундный. Это преобразование сильно уменьшает энергию лазера, она падает от наноджоулей до пикождоулей. Ученые мирятся с этим эффектом, потому что луч становится более управляем на подходе к следующему этапу: усилению.

Лекция 14

Дифракция рентгеновских лучей в кристаллах Дифракция рентгеновских лучей - рассеяние рентгеновских лучей кристаллами (или молекулами жидкостей и газов), при котором из начального пучка лучей возникают вторичные отклонённые пучки той же длины волны, появившиеся в результате взаимодействия первичных рентгеновских лучей с электронами вещества; направление и интенсивность вторичных пучков зависят от строения рассеивающего объекта. Явление дифракции рентгеновских лучей, доказывающее их волновую природу, впервые было экспериментально обнаружено на кристаллах немецкими физиками М. Лауэ, В. Фридрихом и П. Книппингом в 1912. Кристалл является естественной трёхмерной дифракционной решеткой для рентгеновских лучей, т. к. расстояние между рассеивающими центрами (атомами) в кристалле одного порядка с длиной волны рентгеновских лучей (~1Å=10 -8 см). М. фон Лауэ

Дифракция рентгеновских лучей на кристаллах можно рассматривать как избирательное отражение рентгеновских лучей от систем атомных плоскостей кристаллической решётки (определяется условием Брэгга-Вульфа). Направление дифракционных максимумов удовлетворяет одновременно трём условиям: a (cos α — cos α 0 ) = Н l, b (cos β — cos β 0) = K l, с (cos γ — cos γ 0) = L l. Здесь a, b, c— периоды кристаллической решетки по трём её осям; α 0, β 0, γ 0 — углы, образуемые падающим, а α, β, γ — рассеянным лучами с осями кристалла; l — длина волны рентгеновских лучей, Н, К, L — целые числа. Эти уравнения называются уравнениями Лауэ.

Формула Вульфа – Брэгга Условие Брэгга — Вульфа – это условие, определяющее положение интерференционных максимумов рентгеновских лучей, рассеянных кристаллом без изменения длины волны. Условие Брэгга-Вульфа установлено в 1913 независимо друг от друга английским учёным У. Л. Брэггом и русским учёным Г. В. Вульфом вскоре после открытия немецким учёным М. Лауэ и его сотрудниками дифракции рентгеновских лучей. Согласно теории Брэгга - Вульфа, максимумы возникают при отражении рентгеновских лучей от системы параллельных кристаллографических плоскостей, когда лучи, отражённые разными плоскостями этой системы, имеют разность хода, равную целому числу длин волн. У. Л. Брэгг

Условие Вульфа - Брэгга можно записать в следующем виде: 2 dsin. J = ml, где d — межплоскостное расстояние, J — угол скольжения, т. е. угол между отражающей плоскостью и падающим лучом, l — длина волны рентгеновского излучения и m — так называемый, порядок отражения, т. е. положительное целое число (Рис. 1)

Естественный и поляризованный свет Естественный свет - это поперечная электромагнитная волна со всевозможными ориентировками вектора Е (а следовательно, и Н ). Плоскополяризованным, или Линейнополяризованным называют свет, в котором вектор Е (а следовательно, и Н) имеет одно единственное направление. Прямые, получающиеся при пересечении плоскости, перпендикулярной направлению распространения света, с плоскостями колебаний для естественного (а), линейнополяризованного (б) и частично поляризованного света (в), показаны на рис. 5 (векторами обозначены направления напряженности электрического поля).

Закон Малюса — физический закон, выражающий зависимость интенсивности линейнополяризованного света после его прохождения через поляризатор от угла ψ между плоскостями поляризации падающего света и поляризатора. где I 0 - интенсивность падающего на поляризатор света, I - интенсивность света, выходящего из поляризатора, kα - коэффициент прозрачности поляризатора. Установлен Э. Л. Малюсом в 1810 году. В релятивистской форме где ω и ώ циклические частоты линейно поляризованных волн, падающей на поляризатор и вышедшей из него. Свет с иной (не линейной) поляризацией может быть представлен в виде суммы двух линейнополяризованных составляющих, к каждой из которых применим закон Малюса. По закону Малюса рассчитываются интенсивности проходящего света во всех поляризационных приборах, например в поляризационных фотометрах и спектрофотометрах. Потери на отражение, зависящие от ψ и не учитываемые законом Малюса, определяются дополнительно.

Поляризация света при отражении и преломлении Если естественный свет падает на границу раздела двух диэлектриков (например, воздуха и стекла), то часть его отражается, а часть преломляется и распространяется во второй среде. Устанавливая на пути отраженного и преломленного лучей анализатор (например, турмалин), убеждаемся в том, что отраженный и преломленный лучи частично поляризованы: при поворачивании анализатора вокруг лучей интенсивность света периодически усиливается и ослабевает (полного гашения не наблюдается!). Дальнейшие исследования показали, что в отраженном луче преобладают колебания, перпендикулярные плоскости падения (на рис. 275 они обозначены точками), в преломленном – колебания, параллельные плоскости падения (изображены стрелками).

Закон Брюстера — закон оптики, выражающий связь показателя преломления с таким углом, при котором свет, отражённый от границы раздела, будет полностью поляризованным в плоскости, перпендикулярной плоскости падения, а преломлённый луч частично поляризуется в плоскости падения, причем поляризация преломленного луча достигает наибольшего значения. Легко установить, что в этом случае отраженный и преломленный лучи взаимно перпендикулярны. Соответствующий угол называется углом Брюстера. Это явление оптики названо по имени шотландского физика Дэвида Брюстера, открывшего в 1815 году. tg(θBr)= n 21 (n 21 - показатель преломления второй среды относительно первой, θBr - угол падения (угол Брюстера)).

При отражении от одной пластинки под углом Брюстера интенсивность линейно поляризованного света очень мала (около 4 % от интенсивности падающего луча). Поэтому для того, чтобы увеличить интенсивность отраженного света (или поляризовать свет, прошедший в стекло, в плоскости, параллельной плоскости падения) применяют несколько скрепленных пластинок, сложенных в стопу — стопу Столетова. Легко проследить по чертежу происходящее. Пусть на верхнюю часть стопы падает луч света. От первой пластины будет отражаться полностью поляризованный луч (около 4 % первоначальной интенсивности), от второй пластины также отразится полностью поляризованный луч (около 3, 75 % первоначальной интенсивности) и так далее. При этом луч, выходящий из стопы снизу, будет все больше поляризоваться в плоскости, параллельной плоскости падения, по мере добавления пластин. Две фотографии оз. Чёрного, сделанные фотоаппаратом без поляризующего фильтра и с ним. На правой фотографии он повёрнут таким образом, что отражённый свет почти полностью отфильтровывается и блики исчезают.

Лекция 15

Поглощение света – это уменьшение интенсивности оптического излучения, проходящего через среду, заполненную веществом, вследствие превращения его в различные виды внутренней энергии вещества. Основным законом, описывающим поглощение, является закон Бугера, связывающий интенсивность пучка света, прошедшего слой поглощающей среды толщиной , с интенсивностью падающего пучка. Закон Бугера был экспериментально установлен в 1729 г. французским физиком П. Бугером и впоследствии теоретически получен немецким ученым И. Ламбертом. Пьер Бугер

Закон Бургера Основным законом, описывающим поглощение, является закон Бугера, связывающий интенсивность I пучка света, прошедшего слой поглощающей среды толщиной x, с интенсивностью падающего пучка I 0. Закон Бугера был экспериментально установлен в 1729 г. французским физиком П. Бугером и впоследствии теоретически получен немецким ученым И. Ламбертом. При этом было высказано предположение, что при прохождении любого слоя вещества интенсивность светового потока уменьшается на определенную долю dl/l, зависящую только от некоторой величины kλ и толщины слоя dx: dl/l=- kλ·dx (1) Решением этого дифференциального уравнения и является закон Бугера I=I 0 e^-kλ·x (2) Величина kλ называется коэффициентом поглощения, причем , как правило, kλ различен для разных длин волн. Иллюстрация закона Бугера — свет (интенсивности I 0) проходит через раствор толщины l.

Рассеяние света — рассеяние электромагнитных волн видимого диапазона при их взаимодействии с веществом. При этом происходит изменение пространственного распределения, частоты, поляризации оптического излучения, хотя часто под рассеянием понимается только преобразование углового распределения светового потока. Пусть ω и ώ - частоты падающего и рассеянного света. Тогда • если ω=ώ – упругое рассеяние • если ω≠ώ – неупругое рассеяние Рассеиваемый свет даёт информацию о структуре и динамике материала. Рассеяние света в оптическом волокне

Закон Рэлея Рэлеевское рассеяние — когерентное рассеяние света без изменения длины волны (называемое также упругим рассеянием) на частицах, неоднородностях или других объектах, когда частота рассеиваемого света существенно меньше собственной частоты рассеивающего объекта или системы. Эквивалентная формулировка: рассеяние света на объектах, размеры которых меньше его длины волны. Названо в честь британского физика лорда Рэлея, установившего зависимость интенсивности рассеянного света от длины волны в 1871 году. В широком смысле так же применяется при описании рассеяния в волновых процессах различной природы. При рэлеевском рассеянии внутреннее состояние рассеивающих частиц не изменяется. Можно рассматривать два предельных случая. Если длина волны меньше расстояния свободного пробега, то акты рассеяния на частицах можно считать независимыми. В противоположном случае, в рассеянии участвуют флуктуации в направлении молекул и в их плотности. Модель взаимодействия с осциллятором Для рассеивания на осцилляторе массы m, с зарядом q и собственной частотой ν 0 и сечения рассеяния σR пропорционально четвёртой степени частоты рассеиваемого света ν:

Цвет зари После захода Солнца вечером темнота наступает не сразу. Небо, особенно в той части горизонта, где зашло Солнце, остается светлым и посылает к земной поверхности постепенно убывающую рассеянную радиацию. Аналогично утром еще до восхода Солнца небо светлеет больше всего в стороне восхода и посылает к земле рассеянный свет. Это явление неполной темноты носит название сумерек вечерних и утренних. Причиной его является освещение Солнцем, находящимся под горизонтом, высоких слоев атмосферы и рассеяние ими солнечного света. Сумерки сопровождаются красивыми, иногда очень эффектными изменениями окраски небесного свода в стороне Солнца. Эти изменения начинаются еще до захода и продолжаются после восхода Солнца. Они имеют довольно закономерный характер и носят название зари. Характерные цвета зари- пурпурный и желтый. Но интенсивность и разнообразие цветовых оттенков зари изменяются в широких пределах в зависимости от содержания аэрозольных примесей в воздухе. Явление зари объясняется рассеянием света мельчайшими частицами атмосферных аэрозолей и дифракцией света на более крупных частицах.

Голубой цвет неба Окраска безоблачного небесного свода днем, объясняемая рассеянием в атмосфере видимого света. Согласно закону Релея молекулярное рассеяние обратно пропорционально четвертой степени длины волны. Вследствие этого крайние фиолетовые лучи рассеиваются в 14 раз больше, чем крайние красные. Рассеяние крупными частицами обратно пропорционально меньшим степеням длины волны, но и при этом лучи более коротких волн рассеиваются больше, чем более длинных. Поэтому в рассеянном свете, посылаемом небесным сводом, лучи коротковолнового конца видимого спектра, в особенности синие, преобладают над лучами больших длин волн. Фиолетовые лучи рассеиваются больше, чем синие; однако их энергия слишком мала, так же как мала и восприимчивость к ним человеческого глаза. Вследствие этого небесный свод имеет голубой цвет, наиболее интенсивный в зените, где масса воздуха, проходимая солнечными лучами, наименьшая. С высотой небо становится более синим и более темным. При большом содержании в воздухе аэрозолей (пыли и продуктов конденсации) рассеяние все более отклоняется от закона Релея. В этом случае в рассеянном свете возрастает содержание лучей с длинными волнами и небо становится белесоватым. В стратосфере, где плотность и содержание в нем аэрозолей воздуха малы, небо принимает темно-синий и черно-фиолетовый цвет. Синоним: синева неба.

Дисперсия света (разложение света) — это явление, обусловленное зависимостью абсолютного показателя преломления вещества от частоты (или длины волны) света (частотная дисперсия), или, то же самое, зависимость фазовой скорости света в веществе от длины волны (или частоты). Экспериментально открыта Ньютоном около 1672 года, хотя теоретически достаточно хорошо объяснена значительно позднее. • Пространственной дисперсией называется зависимость тензора диэлектрической проницаемости среды от волнового вектора. такая зависимость вызывает ряд явлений, называемых эффектами пространственной поляризации. Один из самых наглядных примеров дисперсии — разложение белого света при прохождении его через призму (опыт Ньютона). Сущностью явления дисперсии является неодинаковая скорость распространения лучей света c различной длиной волны в прозрачном веществе — оптической среде (тогда как в вакууме скорость света всегда одинакова, независимо от длины волны и следовательно цвета). Обычно чем больше частота волны, тем больше показатель преломления среды и меньше ее скорость света в ней: • у красного цвета максимальная скорость в среде и минимальная степень преломления, • у фиолетового цвета минимальная скорость света в среде и максимальная степень преломления.

Дисперсия света позволила впервые вполне убедительно показать составную природу белого света. Белый свет разлагается на спектр и в результате прохождения через дифракционную решётку или отражения от нее (это не связано с явлением дисперсии, а объясняется природой дифракции). Дифракционный и призматический спектры несколько отличаются: призматический спектр сжат в красной части и растянут в фиолетовой и располагается в порядке убывания длины волны: от красного к фиолетовому; нормальный (дифракционный) спектр — равномерный во всех областях и располагается в порядке возрастания длин волн: от фиолетового к красному. По аналогии с дисперсией света, также дисперсией называются и сходные явления зависимости распространения волн любой другой природы от длины волны (или частоты). По этой причине, например, термин закон дисперсии, применяемый как название количественного соотношения, связывающего частоту и волновое число, применяется не только к электромагнитной волне, но к любому волновому процессу. Дисперсией объясняется факт появления радуги после дождя (точнее тот факт, что радуга разноцветная, а не белая). Дисперсия является причиной хроматических аберраций — одних из аберраций оптических систем, в том числе фотографических и видео-объективов. Разложение света в спектр вследствие дисперсии прохождении через призму (опыт Ньютона) Из-за дисперсии можно наблюдать разные цвета света.

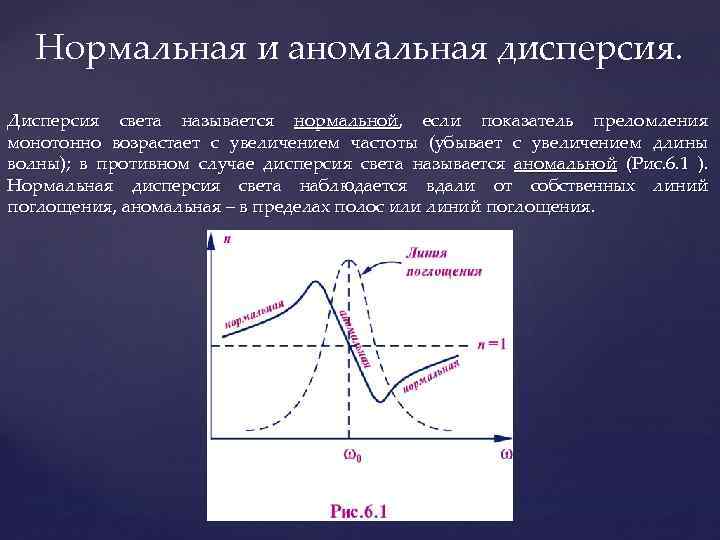Нормальная и аномальная дисперсия. Дисперсия света называется нормальной, если показатель преломления монотонно возрастает с увеличением частоты (убывает с увеличением длины волны); в противном случае дисперсия света называется аномальной (Рис. 6. 1 ). Нормальная дисперсия света наблюдается вдали от собственных линий поглощения, аномальная – в пределах полос или линий поглощения.

История открытия В 1860 году французский физик Леру, проводя измерения показателя преломления для ряда веществ, неожиданно обнаружил, что пары йода преломляют синие лучи в меньшей степени, нежели красные. Леру назвал обнаруженное им явление аномальной дисперсией света. Если при обычной дисперсии показатель преломления с ростом частоты увеличивается, то при аномальной дисперсии показатель преломления, наоборот, уменьшается. Явление аномальной дисперсии было детально исследовано немецким физиком Кундтом в 1871— 1872 гг. Последующие исследования аномальной дисперсии света показали, что наиболее интересные экспериментальные результаты получаются, когда вместо двух скрещенных призм используется, например, призма и интерферометр. Такая экспериментальная методика была применена известным русским Август Адольф Эдуард Эберхард Кундт физиком Д. С. Рождественским в начале XX века.

Благодарю за внимание!