10_11_prezentatsia.ppt
- Количество слайдов: 21
 Лекции 10 - 11. Пятый постулат Евклида и его равносильность аксиоме параллельности. Эквивалентность пятого постулата Евклида и утверждения Фаракаша Бояи аксиоме параллельности евклидовой геометрии. Предложения Валлиса и Лежандра и аксиома параллельности Литература [2] § 16 ‑ 19
Лекции 10 - 11. Пятый постулат Евклида и его равносильность аксиоме параллельности. Эквивалентность пятого постулата Евклида и утверждения Фаракаша Бояи аксиоме параллельности евклидовой геометрии. Предложения Валлиса и Лежандра и аксиома параллельности Литература [2] § 16 ‑ 19
 Утверждения абсолютной геометрии В равнобедренном треугольнике углы при основании равны между собой. Справедливы первый, второй и третий признаки равенства треугольников. Вертикальные углы равны между собой. Любые два прямых угла конгруэнтны между собой. Через любую точку прямой можно провести перпендикулярную к ней прямую. Теорема о внешнем угле треугольника. Внешний угол треугольника больше любого внутреннего, не смежного с ним.
Утверждения абсолютной геометрии В равнобедренном треугольнике углы при основании равны между собой. Справедливы первый, второй и третий признаки равенства треугольников. Вертикальные углы равны между собой. Любые два прямых угла конгруэнтны между собой. Через любую точку прямой можно провести перпендикулярную к ней прямую. Теорема о внешнем угле треугольника. Внешний угол треугольника больше любого внутреннего, не смежного с ним.
 Аксиома параллельности евклидовой плоскости Если при пересечении двух прямых a и b третьей соответственные углы и равны между собой, то прямые и не пересекаются. Если при пересечении двух прямых a и b третьей прямой с накрест лежащие углы равны между собой, или сумма внутренних односторонних равна развернутому углу, то прямые a и b не пересекаются. V 1. (Аксиома параллельности евклидовой геометрии). Пусть а – произвольная прямая, А – точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не более одной прямой, проходящей через А и не пересекающей прямую а.
Аксиома параллельности евклидовой плоскости Если при пересечении двух прямых a и b третьей соответственные углы и равны между собой, то прямые и не пересекаются. Если при пересечении двух прямых a и b третьей прямой с накрест лежащие углы равны между собой, или сумма внутренних односторонних равна развернутому углу, то прямые a и b не пересекаются. V 1. (Аксиома параллельности евклидовой геометрии). Пусть а – произвольная прямая, А – точка, не лежащая на этой прямой. Тогда в плоскости, определяемой точкой А и прямой а, существует не более одной прямой, проходящей через А и не пересекающей прямую а.
 Пятый постулат Евклида и аксиома параллельности Пятый постулат Евклида. Если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше двух прямых, то эти прямые пересекались бы при достаточном продолжении с этой стороны. Теорема. Пятый постулат Евклида эквивалентен аксиоме параллельности евклидовой плоскости.
Пятый постулат Евклида и аксиома параллельности Пятый постулат Евклида. Если две прямые при пересечении с третьей образуют с одной стороны внутренние односторонние углы, сумма которых меньше двух прямых, то эти прямые пересекались бы при достаточном продолжении с этой стороны. Теорема. Пятый постулат Евклида эквивалентен аксиоме параллельности евклидовой плоскости.
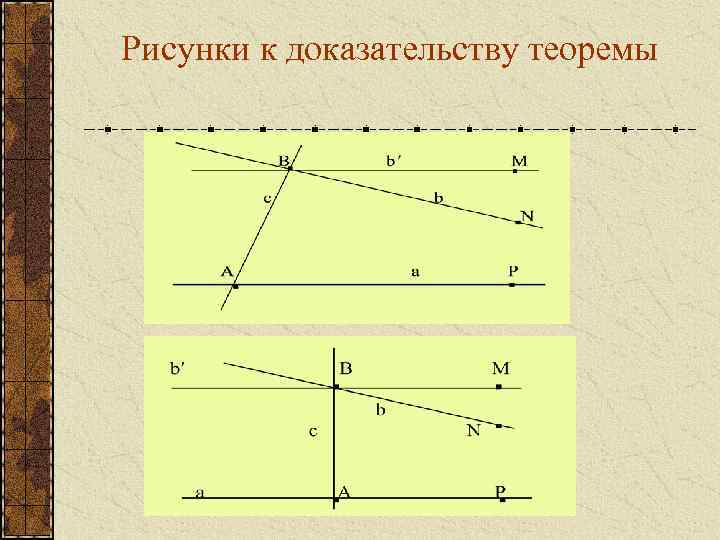 Рисунки к доказательству теоремы
Рисунки к доказательству теоремы
 Свойство серединных перпендикуляров к сторонам треугольника Если вокруг треугольника можно описать окружности, то ее центр лежит в точке пересечения серединных перпендикуляров. Наоборот, если два серединных перпендикуляра треугольника пересекаются, то их общая точка служит центром описанной окружности этого треугольника и через эту точку проходит серединный перпендикуляр к третьей стороне.
Свойство серединных перпендикуляров к сторонам треугольника Если вокруг треугольника можно описать окружности, то ее центр лежит в точке пересечения серединных перпендикуляров. Наоборот, если два серединных перпендикуляра треугольника пересекаются, то их общая точка служит центром описанной окружности этого треугольника и через эту точку проходит серединный перпендикуляр к третьей стороне.
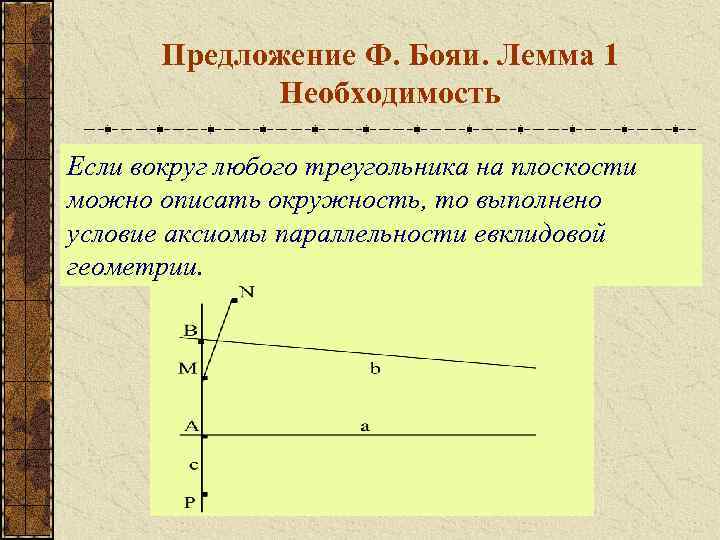 Предложение Ф. Бояи. Лемма 1 Необходимость Если вокруг любого треугольника на плоскости можно описать окружность, то выполнено условие аксиомы параллельности евклидовой геометрии.
Предложение Ф. Бояи. Лемма 1 Необходимость Если вокруг любого треугольника на плоскости можно описать окружность, то выполнено условие аксиомы параллельности евклидовой геометрии.
 Обратно. Предположим, что, через точку, не лежащую на данной прямой, проходит не более одной прямой, не пересекающей данную. Тогда если прямые не пересекаются, то при пересечении третьей прямой накрест лежащие углы равны между собой. Рассмотрим треугольник АВС. Пусть М и N середины сторон АВ и АС, а m и n соответственно серединные перпендикуляры, восставленные в этих точках (рис а). Предположим, что серединные перпендикуляры m и n не пересекаются (рис б). Тогда углы между прямыми АС и n и прямыми АВ и m – прямые. Прямая АС пересекает прямую m. Поэтому, в силу признака параллельности прямых на евклидовой плоскости угол между m и АС прямой. С другой стороны, прямая m серединный перпендикуляр к прямой АВ. Таким образом, из точки А мы провели два перпендикуляра к прямой m, чего не может быть. Построенное противоречие опровергает наше предположение, серединные перпендикуляры m и n пересекаются. Вокруг любого треугольника на евклидовой плоскости можно описать окружность.
Обратно. Предположим, что, через точку, не лежащую на данной прямой, проходит не более одной прямой, не пересекающей данную. Тогда если прямые не пересекаются, то при пересечении третьей прямой накрест лежащие углы равны между собой. Рассмотрим треугольник АВС. Пусть М и N середины сторон АВ и АС, а m и n соответственно серединные перпендикуляры, восставленные в этих точках (рис а). Предположим, что серединные перпендикуляры m и n не пересекаются (рис б). Тогда углы между прямыми АС и n и прямыми АВ и m – прямые. Прямая АС пересекает прямую m. Поэтому, в силу признака параллельности прямых на евклидовой плоскости угол между m и АС прямой. С другой стороны, прямая m серединный перпендикуляр к прямой АВ. Таким образом, из точки А мы провели два перпендикуляра к прямой m, чего не может быть. Построенное противоречие опровергает наше предположение, серединные перпендикуляры m и n пересекаются. Вокруг любого треугольника на евклидовой плоскости можно описать окружность.
 Предложение Ф. Бояи Утверждение: вокруг любого треугольника на плоскости можно описать окружность, равносильно аксиоме параллельности евклидовой геометрии.
Предложение Ф. Бояи Утверждение: вокруг любого треугольника на плоскости можно описать окружность, равносильно аксиоме параллельности евклидовой геометрии.
 Первая теорема Лежандра Сумма углов треугольника не может превышать двух прямых углов. Первое вспомогательное утверждение. Сумму углов произвольного треугольника АВС будем обозначать через (АВС). Пусть дан произвольный треугольник АВС, тогда существует такой треугольник, у которого, во первых, угол А 1 меньше или равен половине угла А треугольника АВС: , и, во вторых, .
Первая теорема Лежандра Сумма углов треугольника не может превышать двух прямых углов. Первое вспомогательное утверждение. Сумму углов произвольного треугольника АВС будем обозначать через (АВС). Пусть дан произвольный треугольник АВС, тогда существует такой треугольник, у которого, во первых, угол А 1 меньше или равен половине угла А треугольника АВС: , и, во вторых, .
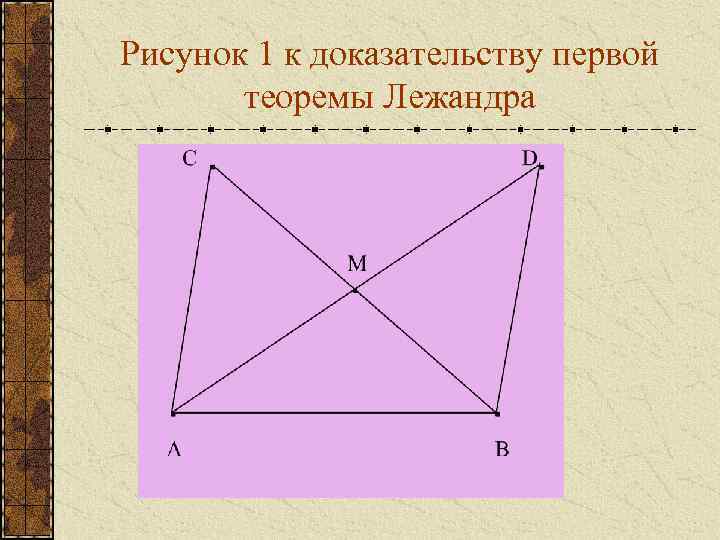 Рисунок 1 к доказательству первой теоремы Лежандра
Рисунок 1 к доказательству первой теоремы Лежандра
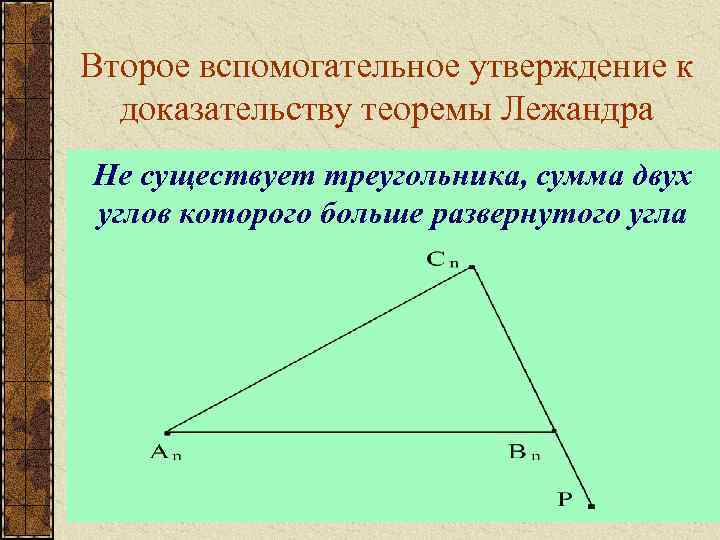 Второе вспомогательное утверждение к доказательству теоремы Лежандра Не существует треугольника, сумма двух углов которого больше развернутого угла
Второе вспомогательное утверждение к доказательству теоремы Лежандра Не существует треугольника, сумма двух углов которого больше развернутого угла
 Вторая теорема Лежандра Если на плоскости существует хотя бы один треугольник, сумма углов которого равна двум прямым углам, то сумма углов любого другого треугольника также равна развернутому углу.
Вторая теорема Лежандра Если на плоскости существует хотя бы один треугольник, сумма углов которого равна двум прямым углам, то сумма углов любого другого треугольника также равна развернутому углу.
 Эквивалентность аксиомы параллельности евклидовой геометрии теореме о сумме углов треугольника Предположение о существовании треугольника, сумма углов которого совпадает с суммой двух прямых углов, равносильно аксиоме параллельности евклидовой плоскости. Лемма: Сумма углов треугольника равна 2 d тогда и только тогда, когда его внешний угол равен сумме внутренних углов, с ним не смежных.
Эквивалентность аксиомы параллельности евклидовой геометрии теореме о сумме углов треугольника Предположение о существовании треугольника, сумма углов которого совпадает с суммой двух прямых углов, равносильно аксиоме параллельности евклидовой плоскости. Лемма: Сумма углов треугольника равна 2 d тогда и только тогда, когда его внешний угол равен сумме внутренних углов, с ним не смежных.
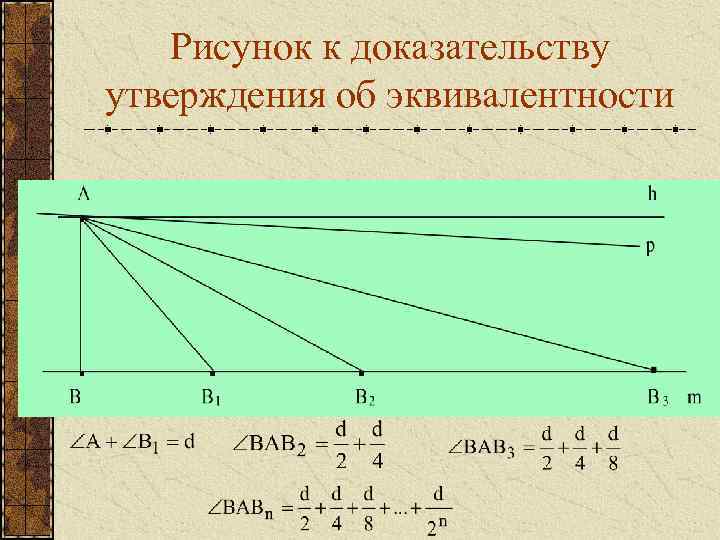 Рисунок к доказательству утверждения об эквивалентности
Рисунок к доказательству утверждения об эквивалентности
 Предложение Валлиса. На плоскости существует хотя бы одна пара треугольников с соответственно равными углами, но не равными сторонами. Предложение Валлиса эквивалентно аксиоме параллельности евклидовой геометрии.
Предложение Валлиса. На плоскости существует хотя бы одна пара треугольников с соответственно равными углами, но не равными сторонами. Предложение Валлиса эквивалентно аксиоме параллельности евклидовой геометрии.
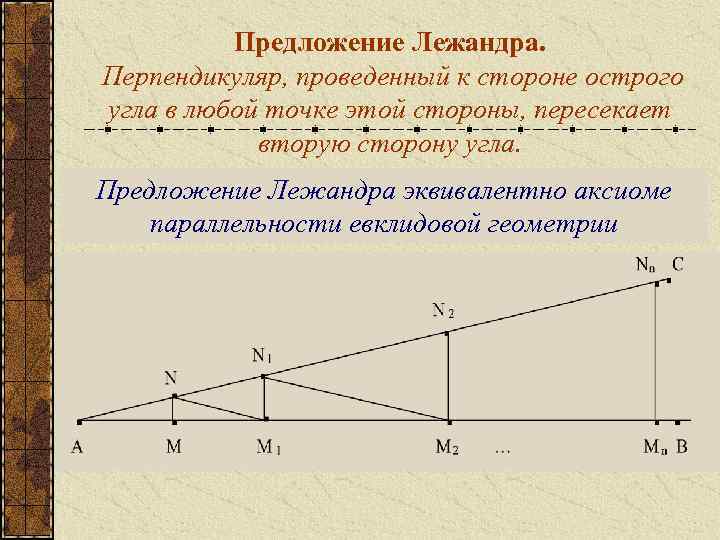 Предложение Лежандра. Перпендикуляр, проведенный к стороне острого угла в любой точке этой стороны, пересекает вторую сторону угла. Предложение Лежандра эквивалентно аксиоме параллельности евклидовой геометрии
Предложение Лежандра. Перпендикуляр, проведенный к стороне острого угла в любой точке этой стороны, пересекает вторую сторону угла. Предложение Лежандра эквивалентно аксиоме параллельности евклидовой геометрии
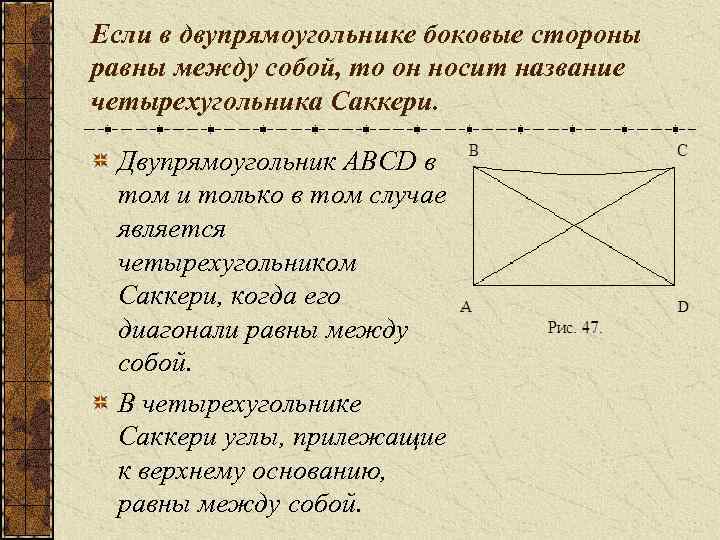 Если в двупрямоугольнике боковые стороны равны между собой, то он носит название четырехугольника Саккери. Двупрямоугольник ABCD в том и только в том случае является четырехугольником Саккери, когда его диагонали равны между собой. В четырехугольнике Саккери углы, прилежащие к верхнему основанию, равны между собой.
Если в двупрямоугольнике боковые стороны равны между собой, то он носит название четырехугольника Саккери. Двупрямоугольник ABCD в том и только в том случае является четырехугольником Саккери, когда его диагонали равны между собой. В четырехугольнике Саккери углы, прилежащие к верхнему основанию, равны между собой.
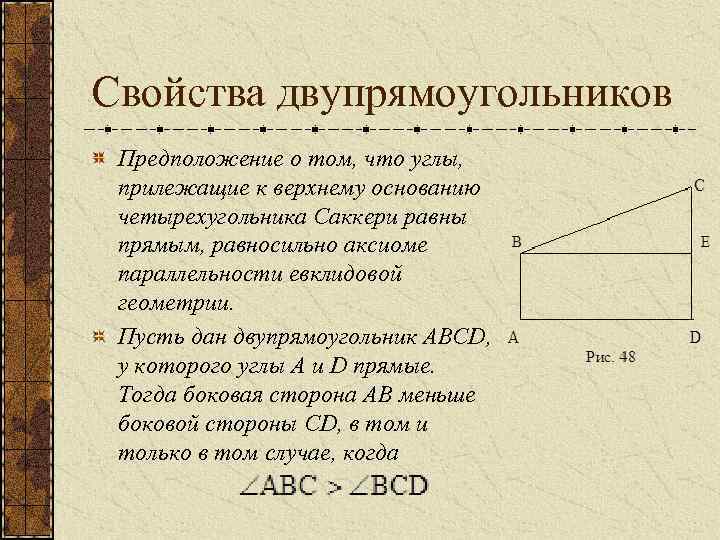 Свойства двупрямоугольников Предположение о том, что углы, прилежащие к верхнему основанию четырехугольника Саккери равны прямым, равносильно аксиоме параллельности евклидовой геометрии. Пусть дан двупрямоугольник ABCD, у которого углы А и D прямые. Тогда боковая сторона АВ меньше боковой стороны CD, в том и только в том случае, когда
Свойства двупрямоугольников Предположение о том, что углы, прилежащие к верхнему основанию четырехугольника Саккери равны прямым, равносильно аксиоме параллельности евклидовой геометрии. Пусть дан двупрямоугольник ABCD, у которого углы А и D прямые. Тогда боковая сторона АВ меньше боковой стороны CD, в том и только в том случае, когда
 Свойство четырехугольника Саккери Двупрямоугольник тогда и только тогда является четырехугольником Саккери, когда углы, прилежащие к верхнему основанию, равны между собой.
Свойство четырехугольника Саккери Двупрямоугольник тогда и только тогда является четырехугольником Саккери, когда углы, прилежащие к верхнему основанию, равны между собой.
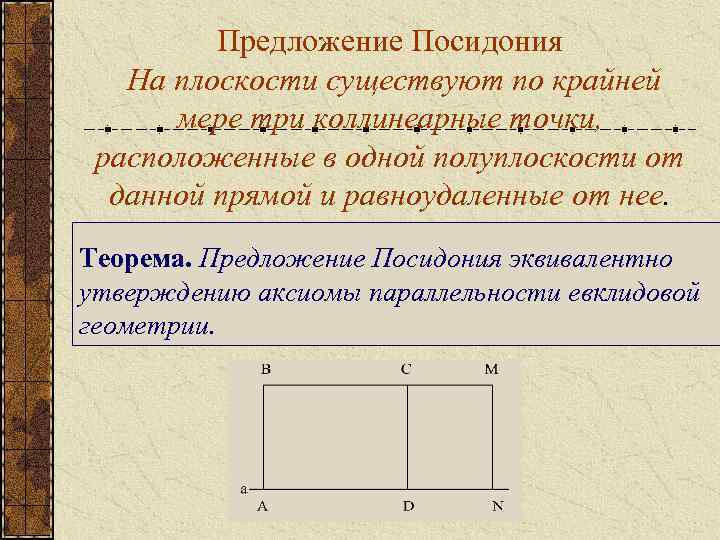 Предложение Посидония На плоскости существуют по крайней мере три коллинеарные точки, расположенные в одной полуплоскости от данной прямой и равноудаленные от нее. Теорема. Предложение Посидония эквивалентно утверждению аксиомы параллельности евклидовой геометрии.
Предложение Посидония На плоскости существуют по крайней мере три коллинеарные точки, расположенные в одной полуплоскости от данной прямой и равноудаленные от нее. Теорема. Предложение Посидония эквивалентно утверждению аксиомы параллельности евклидовой геометрии.


