Lekce — Automaty a regularní výrazy Evropská unie

Lekce - Automaty a regularní výrazy Evropská unie Evropský sociální fond Praha & EU: Investujeme do vaší budoucnosti

Automat Hrací skřínka, Leopold Aucac Aine, Paris

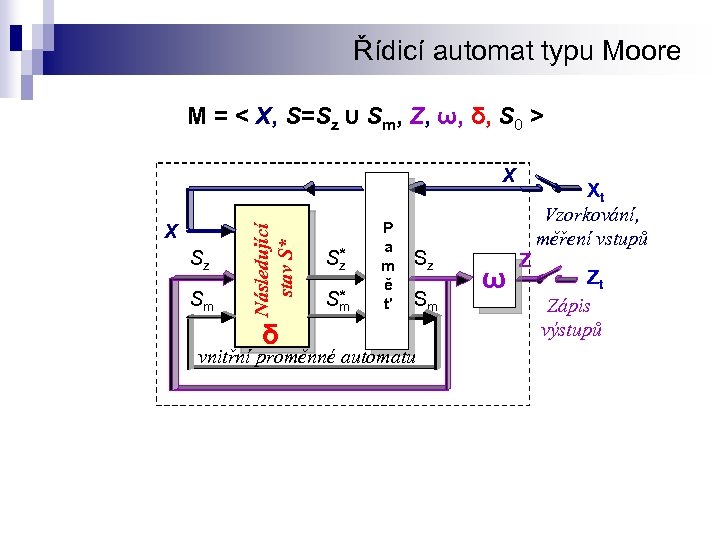Řídicí automat typu Moore M = < X, S=Sz ∪ Sm, Z, ω, δ, S 0 > X Sz Sm Následující stav S* X δ S* z S* m P a m ě ť Sz Sm vnitřní proměnné automatu ω Z Xt Vzorkování, měření vstupů Zt Zápis výstupů

Definice konečného automatu FSM – Finite State Machine Uspořádaná šestice M = < X, S, Z, ω, δ, s 0 > n n n X - konečná množina všech vstupních vektorů Z - konečná množina všech výstupních vektorů S - konečná množina všech vnitřních stavů δ - přechodová funkce - zobrazení δ: X x S -> S ω - výstupní funkce - zobrazení ω: ω: S -> Z (Moore) ω: X x S -> Z (Mealy) s 0 - počáteční stav S 0 S

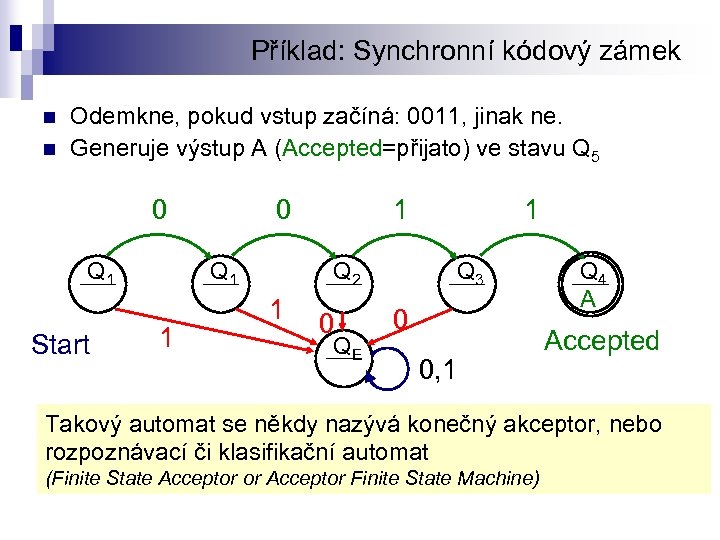Příklad: Synchronní kódový zámek n n Odemkne, pokud vstup začíná: 0011, jinak ne. Generuje výstup A (Accepted=přijato) ve stavu Q 5 0 Q 1 Start 0 Q 1 1 1 1 Q 2 0 QE 0 1 Q 3 0, 1 Q 4 A Accepted Takový automat se někdy nazývá konečný akceptor, nebo rozpoznávací či klasifikační automat (Finite State Acceptor or Acceptor Finite State Machine)

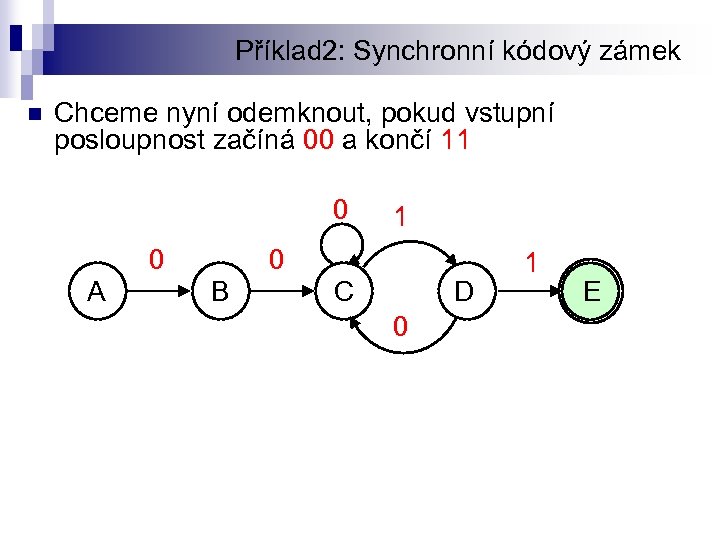Příklad 2: Synchronní kódový zámek n Chceme nyní odemknout, pokud vstupní posloupnost začíná 00 a končí 11 0 0 A 1 0 B C D 0 1 E

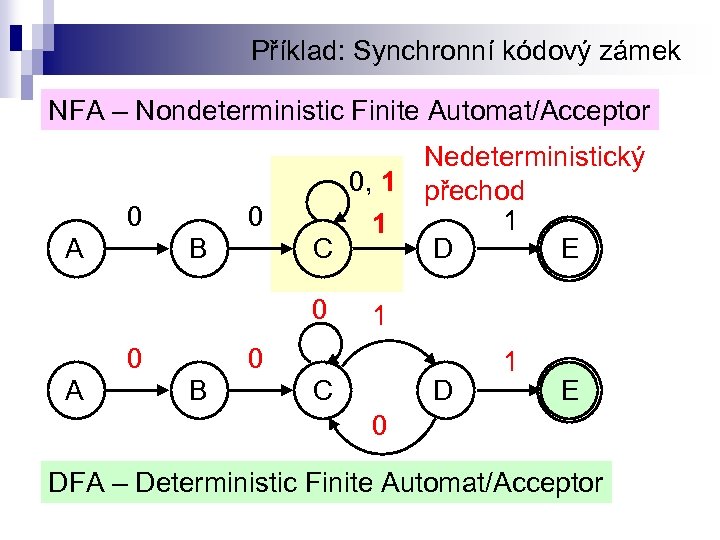Příklad: Synchronní kódový zámek NFA – Nondeterministic Finite Automat/Acceptor 0 A 0 B Nedeterministický 0, 1 přechod 1 1 C D E 0 0 A 1 0 B C D 1 E 0 DFA – Deterministic Finite Automat/Acceptor

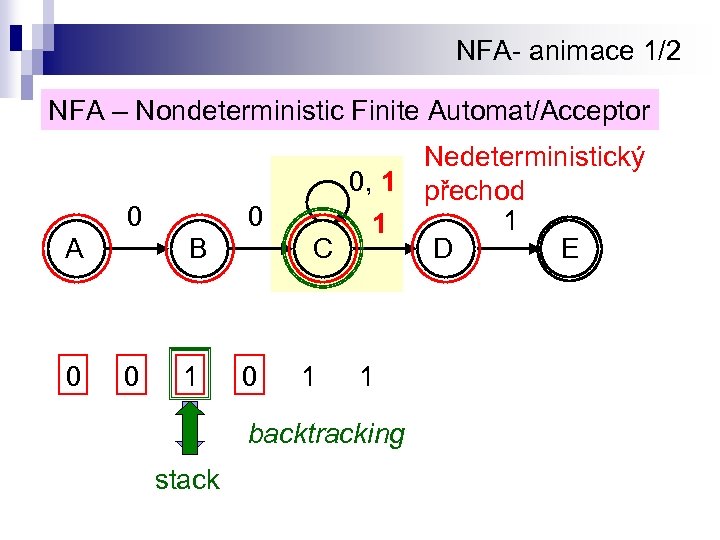NFA- animace 1/2 NFA – Nondeterministic Finite Automat/Acceptor 0 A 0 0 B 0 1 0 Nedeterministický 0, 1 přechod 1 1 C D E 1 1 backtracking stack

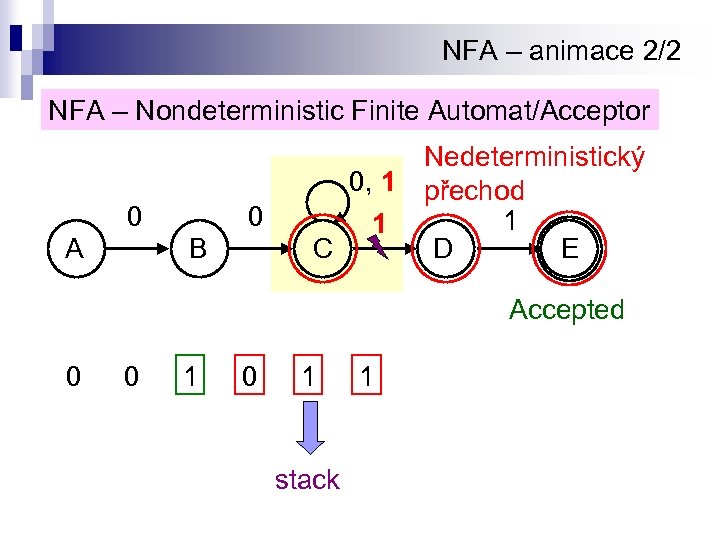NFA – animace 2/2 NFA – Nondeterministic Finite Automat/Acceptor 0 A 0 B Nedeterministický 0, 1 přechod 1 1 C D E Accepted 0 0 1 stack 1

Nedeterministické chování není náhodné Deterministické: f(1) → 1 vždy n Náhodné: f(1) → 1 v 50% případů, f(1) → 2 v ostatních situacích n Nedeterministické chování f(1) → 1 nebo f(1) → 2, ale nepovíme, kdy tomu tak bude. n Nedeterministické chování může vypadat deterministicky, náhodně, nebo i hůře n

Definice konečného akceptoru Uspořádaná pětice M = < X, S, δ, s 0, F > n n X - konečná množina všech vstupních vektorů S - konečná množina všech vnitřních stavů n δ - přechodová funkce ¨ pro DFA - zobrazení δ: X x S -> S ¨ pro NFA – zobrazení δ: {X + ε} x S -> množina S, kde ε je prázdný vstup n s 0 - počáteční stav s 0 S n F – množina (i prázdná) koncových stavů F S

DFA versus NFA se dají mnohem rychleji sestavit, ale obtížněji se prochází jejich stavovým diagramem – musíme si pamatovat stavy a případně se vracet. n NFA s více koncovými stavy lze vždy převést na NFA s jedním koncovým stavem. n NFA lze vždy převést na DFA, ale odpovídající DFA reprezentace může mít exponenciální nárůst počtu stavů nebo přechodů. n

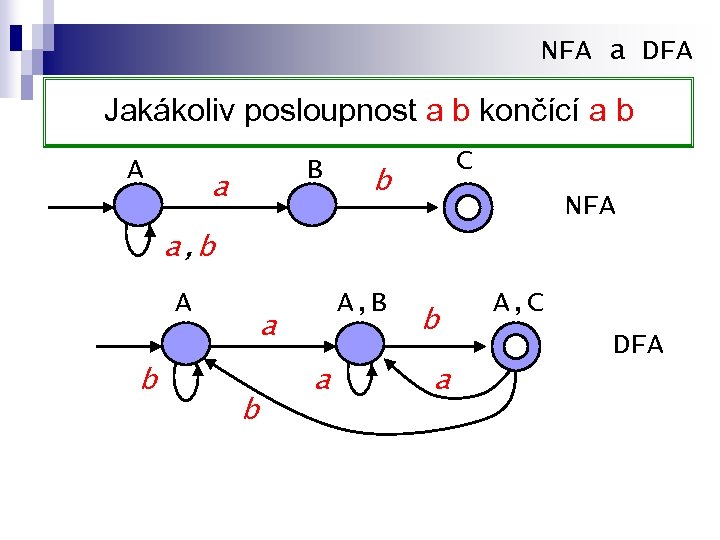NFA a DFA Jakákoliv posloupnost a b končící a b A B a C b NFA a, b A A, B a b b a A, C DFA

Jazyky The Tower of Babel, Pieter Brueghel, c. 1563, Kunsthistorisches Museum, Vienna

Automaty rozpoznávají jazyk Abeceda (Alphabet) – konečná množina znaků n Slovo (String) – konečná posloupnost znaku – může být prázdná e, (prázdné slovo se v některých textech označuje i jako l) n Jazyk (Language) – množina, případně i nekonečná, všech slov utvořených z abecedy – množina může být i prázdný { }, tj. prázdný jazyk. n

Příklady jazyků Předpokládejme S = {a, b, c}, pak lze z S utvořit například jazyky: ¨ {aa, ab, ac, bb, bc, cc} ¨ {ab, abcc, abccc, . . . } ¨ { e } ¨ {a, b, c, e}

Regulární jazyky n Regulární jazyky jsou jazyky rozpoznávané pomocí NFA nebo DFA. n Akceptory, které rozpoznávají regulární jazyky, se popisují regulárními výrazy. n Java, PHP, Python, C# a další, implementují regulární výrazy zpravidla pomocí NFA, která se dá rychleji sestavit.

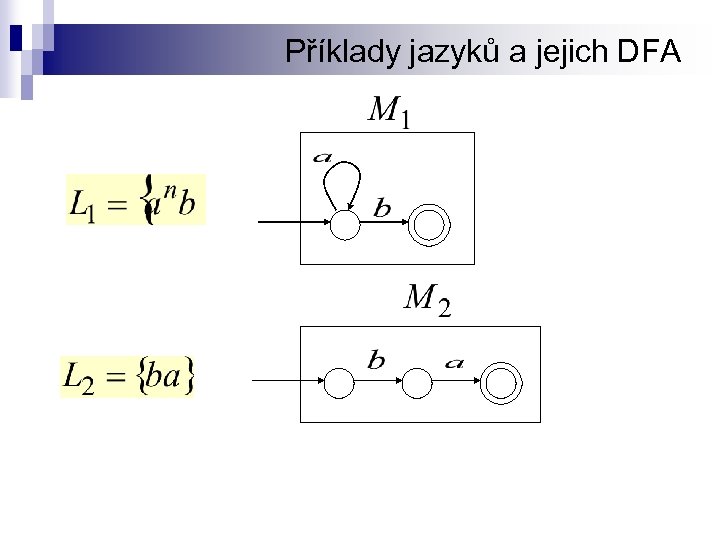Příklady jazyků a jejich DFA

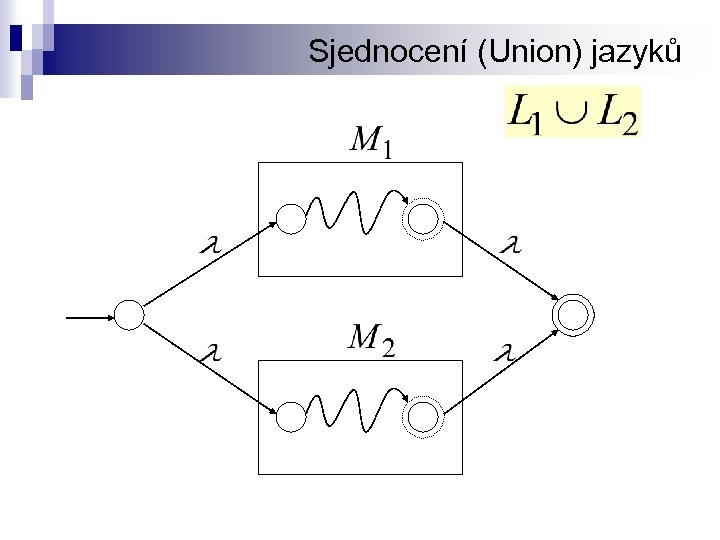Sjednocení (Union) jazyků

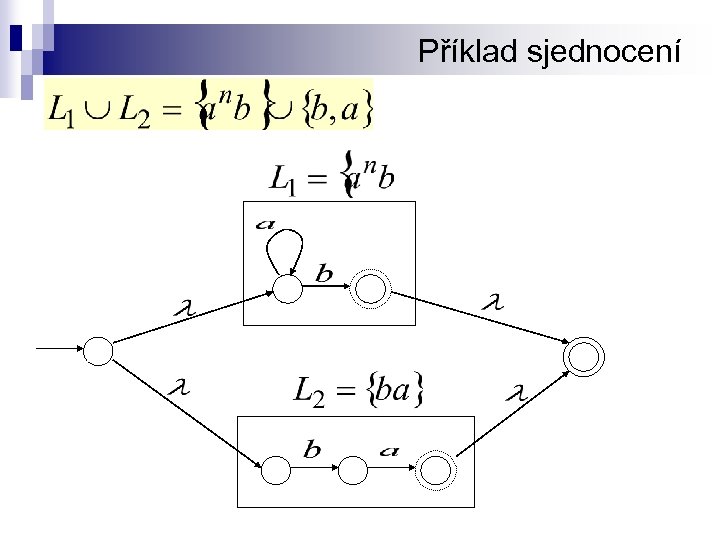Příklad sjednocení

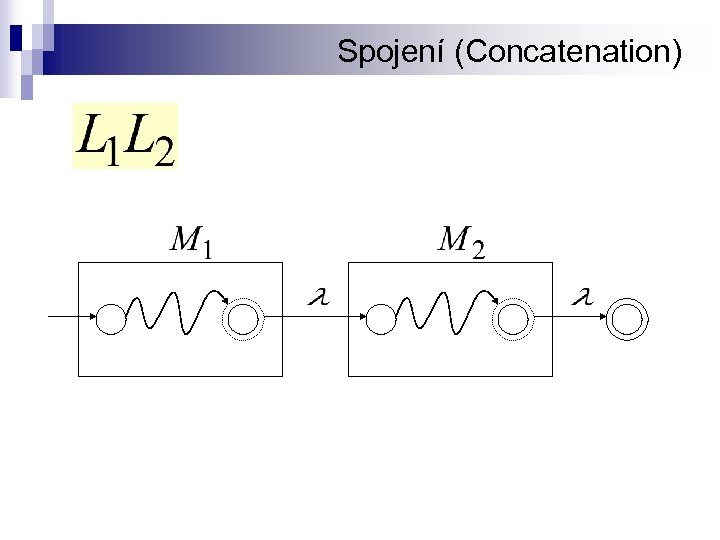Spojení (Concatenation)

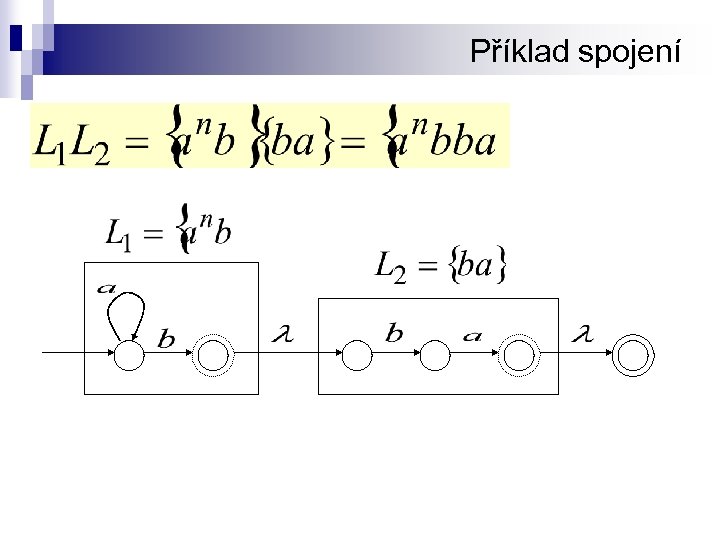Příklad spojení

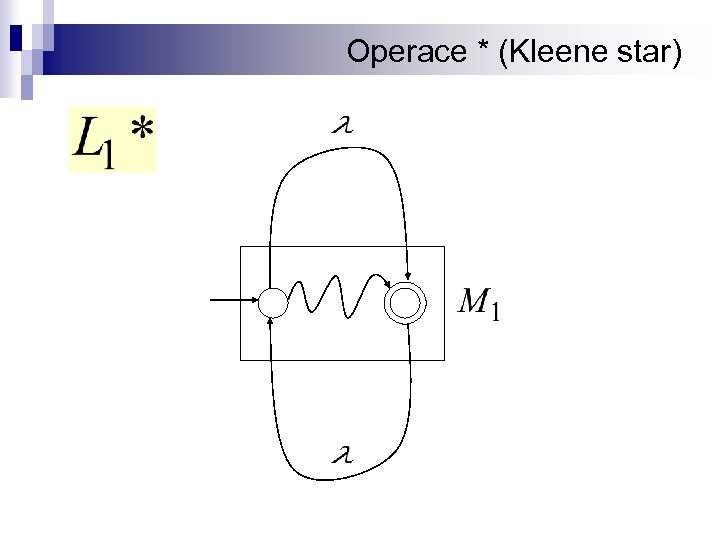Operace * (Kleene star)

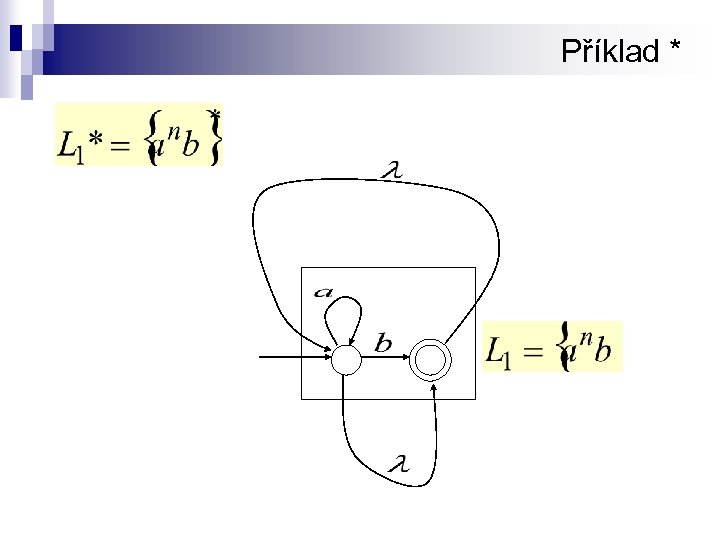Příklad *

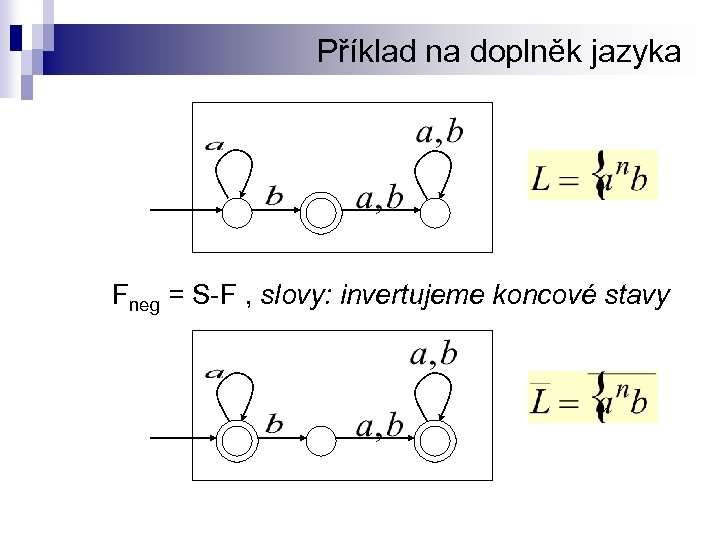Příklad na doplněk jazyka Fneg = S-F , slovy: invertujeme koncové stavy

Regulární výrazy http: //www. dotnetcoders. com/web/Learning/Regex/default. aspx

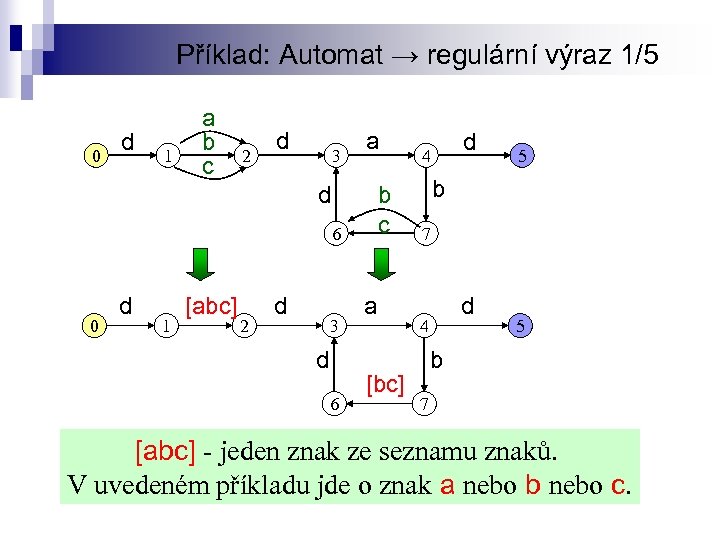Příklad: Automat → regulární výraz 1/5 0 d 1 a b c 2 d 3 a d b c 6 0 d 1 [abc] 2 d 3 d 6 a [bc] d 4 5 b 7 [abc] - jeden znak ze seznamu znaků. V uvedeném příkladu jde o znak a nebo b nebo c.

Příklad: Automat → regulární výraz 2/5 0 d 1 [abc] d 2 3 d 6 d[abc]d 0 a [bc] 4 5 b 7 a 3 d d 4 b[bc]d 5

Příklad: Automat → regulární výraz 3/5 d[abc]d 0 a 3 d 4 5 b[bc]d d[abc]d 0 a 3 d 4 b[bc]da b(b|c)da 5

Příklad: Automat → regulární výraz 4/5 d[abc]d 0 a 3 d 4 5 b[bc]da d[abc]d 0 a 3 (b[bc]da)*d 4 5

Příklad: Automat → regulární výraz 5/5 d[abc]d 0 a 3 (b[bc]da)*d 4 5 d[abc]da(b[bc]da)*d 0 5 * - 0 nebo více znaků ze seznamu. V uvedeném příkladu jde o skupinu (b[bc]da)

Neregulární jazyky n Pro neregulární jazyky nelze navrhnout NFA nebo DFA. Nelze je ani popsat regulárním výrazem. n Příklad: jazyk W = {anbn | n>0}

Regulární výrazy: Metacharacters n Začátečníkům pomůže knihovna regulárních výrazů http: //regexlib. com/ n Některé "character-class" metacharacters ¨ d – libovolné číslo D – nečíselný znak ¨ w – libovolný znak slova W – neslovní znak ¨ s – oddělovač "whitespace" S – není "whitespace" n Příklad ddds nalezne: "123 456"

Některé uživatelské znaky Jeden znak s výjimkou konce řádku "newline". Např. a. a určuje aea, aia, aca, and a a [XY] Jeden znak ze seznamu znaků. V uvedeném příkladu jde o znak X nebo Y [A-Z] Jeden znak z rozsahu od A do Z (v příkladu pouze velká písmena). [A-Za-z] Jeden znak, malá nebo velká písmena A až Z [^AB] Jeden znak různý od A nebo B .

Modifikátory výrazu ^ $ Následující znak je literal, ne "metacharacter" Následující výraz se musí se objevit na začátku textu Následující výraz se musí objevit na konci textu "^Kolo" nalezne "Kolohnát", ale nikoliv "Moje Kolo" "stroj$" matches "Nástroj", ale ne "stroje"

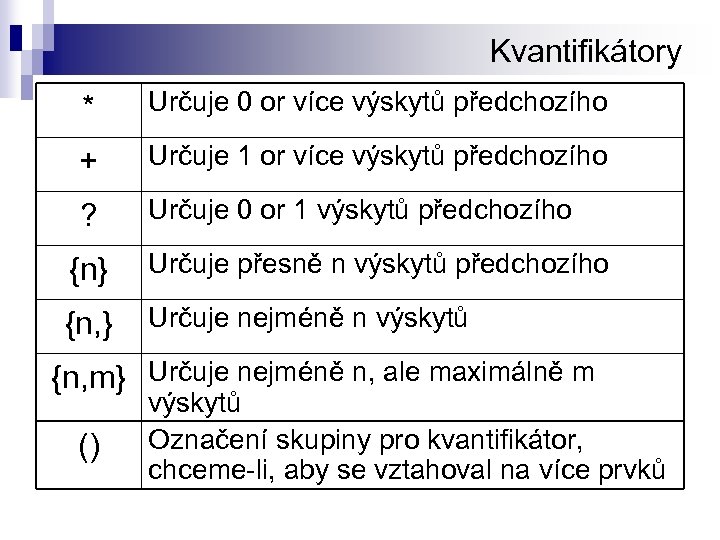Kvantifikátory * Určuje 0 or více výskytů předchozího + Určuje 1 or více výskytů předchozího ? Určuje 0 or 1 výskytů předchozího {n} Určuje přesně n výskytů předchozího {n, } Určuje nejméně n výskytů {n, m} Určuje nejméně n, ale maximálně m () výskytů Označení skupiny pro kvantifikátor, chceme-li, aby se vztahoval na více prvků

Jaká je správná odpověď?

Ukázka programu v |Java import java. util. regex. Matcher; import java. util. regex. Pattern; public class Date. Matcher { public Date. Matcher() { String a. Date = "date: 12 -15 -2003"; Pattern date. Pattern = Pattern. compile( "date: (\d{2})-(\d{4})"); Matcher date. Matcher = date. Pattern. matcher(a. Date); if (date. Matcher. find()) { System. out. println("Month is: " + date. Matcher. group(1)); System. out. println("Day is: " + date. Matcher. group(2)); System. out. println("Year is: " + date. Matcher. group(3)); } } public static void main(String[] args) { new Date. Matcher(); } }

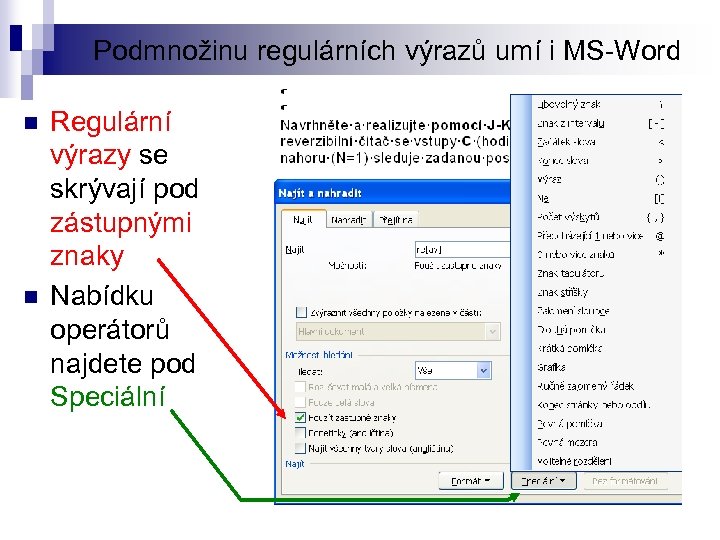Podmnožinu regulárních výrazů umí i MS-Word n n Regulární výrazy se skrývají pod zástupnými znaky Nabídku operátorů najdete pod Speciální