Лек. 4. ДИНАМИКА ВРАЩЕНИЙ






































Динамика вращательного движение 2014.ppt
- Количество слайдов: 51
 Лек. 4. ДИНАМИКА ВРАЩЕНИЙ
Лек. 4. ДИНАМИКА ВРАЩЕНИЙ
 Векторное произведение двух векторов. Векторным произведением двух векторов A и B называется вектор С, величина которого равна при этом векторы A, B и C образуют правую тройку. Направление вектора C можно определить по правилу буравчика. Если вращать ручку правого винта (буравчика) от вектора А, к вектору B по направлению наименьшего угла между ними, то направление вектора С совпадёт с поступательным движением винта (буравчика). Векторное произведение обозначают так: Правую тройку образуют также и координатные оси в декартовой системе координат.
Векторное произведение двух векторов. Векторным произведением двух векторов A и B называется вектор С, величина которого равна при этом векторы A, B и C образуют правую тройку. Направление вектора C можно определить по правилу буравчика. Если вращать ручку правого винта (буравчика) от вектора А, к вектору B по направлению наименьшего угла между ними, то направление вектора С совпадёт с поступательным движением винта (буравчика). Векторное произведение обозначают так: Правую тройку образуют также и координатные оси в декартовой системе координат.
 Абсолютно твёрдое тело. Абсолютно твёрдым телом называется такое тело, для которого радиус-вектор, соединяющий две любые точки этого тела не изменяется ни при каких воздействиях на это тело. Абсолютно твёрдое тело можно разбить (мысленно) на материальные точки, каждая из которых обладает некоторой массой. Тогда массу всего тела можно представить, как В отличие от материальной точки твёрдое тело может совершать вращательное движение. Напомним, что для описания вращательного движения удобно использовать следующие величины: - вектор углового перемещения; - вектор угловой скорости; - вектор углового ускорения.
Абсолютно твёрдое тело. Абсолютно твёрдым телом называется такое тело, для которого радиус-вектор, соединяющий две любые точки этого тела не изменяется ни при каких воздействиях на это тело. Абсолютно твёрдое тело можно разбить (мысленно) на материальные точки, каждая из которых обладает некоторой массой. Тогда массу всего тела можно представить, как В отличие от материальной точки твёрдое тело может совершать вращательное движение. Напомним, что для описания вращательного движения удобно использовать следующие величины: - вектор углового перемещения; - вектор угловой скорости; - вектор углового ускорения.
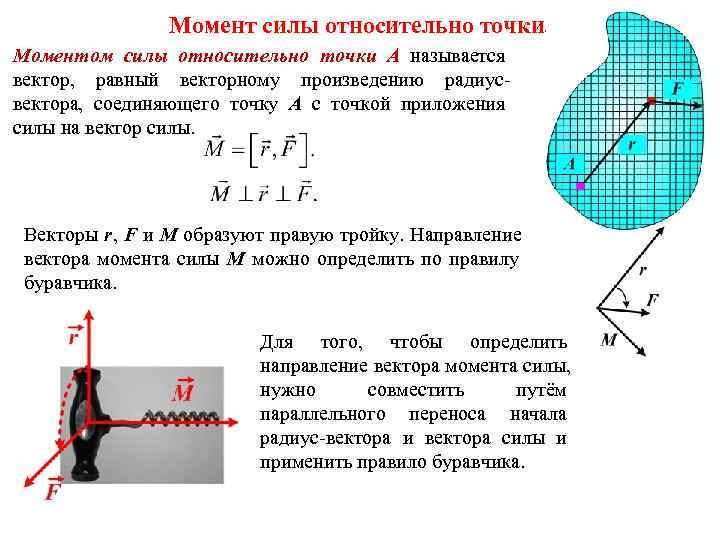
 Момент силы относительно точки. Моментом силы относительно точки A называется вектор, равный векторному произведению радиус- вектора, соединяющего точку A с точкой приложения силы на вектор силы. Векторы r, F и M образуют правую тройку. Направление вектора момента силы М можно определить по правилу буравчика. Для того, чтобы определить направление вектора момента силы, нужно совместить путём параллельного переноса начала радиус-вектора и вектора силы и применить правило буравчика.
Момент силы относительно точки. Моментом силы относительно точки A называется вектор, равный векторному произведению радиус- вектора, соединяющего точку A с точкой приложения силы на вектор силы. Векторы r, F и M образуют правую тройку. Направление вектора момента силы М можно определить по правилу буравчика. Для того, чтобы определить направление вектора момента силы, нужно совместить путём параллельного переноса начала радиус-вектора и вектора силы и применить правило буравчика.
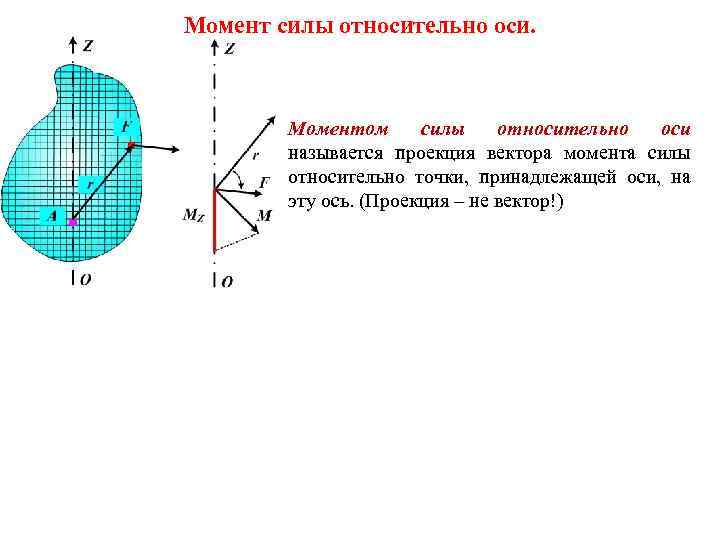
 Момент силы относительно оси. Моментом силы относительно оси называется проекция вектора момента силы относительно точки, принадлежащей оси, на эту ось. (Проекция – не вектор!)
Момент силы относительно оси. Моментом силы относительно оси называется проекция вектора момента силы относительно точки, принадлежащей оси, на эту ось. (Проекция – не вектор!)
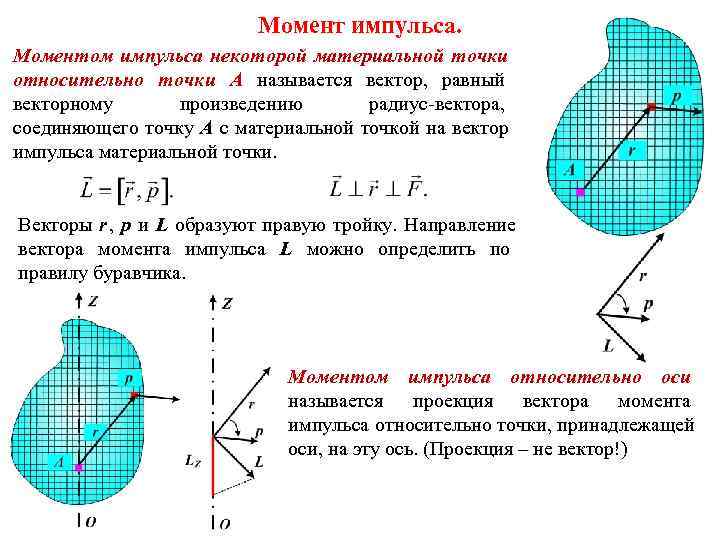
 Момент импульса. Моментом импульса некоторой материальной точки относительно точки A называется вектор, равный векторному произведению радиус-вектора, соединяющего точку A с материальной точкой на вектор импульса материальной точки. Векторы r, p и L образуют правую тройку. Направление вектора момента импульса L можно определить по правилу буравчика. Моментом импульса относительно оси называется проекция вектора момента импульса относительно точки, принадлежащей оси, на эту ось. (Проекция – не вектор!)
Момент импульса. Моментом импульса некоторой материальной точки относительно точки A называется вектор, равный векторному произведению радиус-вектора, соединяющего точку A с материальной точкой на вектор импульса материальной точки. Векторы r, p и L образуют правую тройку. Направление вектора момента импульса L можно определить по правилу буравчика. Моментом импульса относительно оси называется проекция вектора момента импульса относительно точки, принадлежащей оси, на эту ось. (Проекция – не вектор!)
 Момент импульса. Получим формулу для момента импульса тела, вращающегося относительно неподвижной оси. Иногда его называют собственным моментом импульса. Для одной материальной точки Для всего вращающегося тела Импульс одной материальной точки
Момент импульса. Получим формулу для момента импульса тела, вращающегося относительно неподвижной оси. Иногда его называют собственным моментом импульса. Для одной материальной точки Для всего вращающегося тела Импульс одной материальной точки
 Момент инерции. Моментом инерции относительно данной оси называется величина, равная сумме произведений масс материальных точек на квадраты расстояний от точек до оси вращения. Для одной материальной точки Для всего тела Или в форме интеграла Интеграл вычисляется по всему объёму тела.
Момент инерции. Моментом инерции относительно данной оси называется величина, равная сумме произведений масс материальных точек на квадраты расстояний от точек до оси вращения. Для одной материальной точки Для всего тела Или в форме интеграла Интеграл вычисляется по всему объёму тела.
 ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ 4. 1. Момент импульса. Момент силы. Уравнение вращательного движения системы. Рассмотрим движение МТ массой , на которую действует сила ; . – радиус-вектор МТ, проведенный из точки О (начала О), . – ее импульс. Сформулируем два определения. Моментом импульса МТ относительно точки О (начала О) называется величина (4. 1) Моментом силы относительно точки О (начала О) называется величина (4. 2) Если – сумма сил, действующих на МТ (4. 3) то (4. 4) где (4. 5)
ДИНАМИКА ВРАЩАТЕЛЬНОГО ДВИЖЕНИЯ 4. 1. Момент импульса. Момент силы. Уравнение вращательного движения системы. Рассмотрим движение МТ массой , на которую действует сила ; . – радиус-вектор МТ, проведенный из точки О (начала О), . – ее импульс. Сформулируем два определения. Моментом импульса МТ относительно точки О (начала О) называется величина (4. 1) Моментом силы относительно точки О (начала О) называется величина (4. 2) Если – сумма сил, действующих на МТ (4. 3) то (4. 4) где (4. 5)
 Таким образом, в определении (4. 2) под можно понимать сумму (4. 3) сил, приложенных в одной точке. Величина (4. 6) называется моментом инерции тела относительно оси. Тело рассматривается как набор материальных точек , – расстояние от материальной точки до оси. Момент инерции – величина, аддитивная по определению. С учетом определения (4. 6) можно записать: (4. 7) или (4. 8) Величина – момент импульса тела относительно ОZ. Продифференцируем определение (4. 1) по времени: (4. 9) Первое слагаемое в правой части (4. 9) равно нулю, т. к. – это скорость, сонаправленная с импульсом. Используя уравнение движения МТ в импульсной форме (см. лекцию по динамике) получаем (4. 10) Это уравнение вращательного движения МТ (уравнение моментов).
Таким образом, в определении (4. 2) под можно понимать сумму (4. 3) сил, приложенных в одной точке. Величина (4. 6) называется моментом инерции тела относительно оси. Тело рассматривается как набор материальных точек , – расстояние от материальной точки до оси. Момент инерции – величина, аддитивная по определению. С учетом определения (4. 6) можно записать: (4. 7) или (4. 8) Величина – момент импульса тела относительно ОZ. Продифференцируем определение (4. 1) по времени: (4. 9) Первое слагаемое в правой части (4. 9) равно нулю, т. к. – это скорость, сонаправленная с импульсом. Используя уравнение движения МТ в импульсной форме (см. лекцию по динамике) получаем (4. 10) Это уравнение вращательного движения МТ (уравнение моментов).
 Перейдем к описанию движения механической системы. Используем модель – набор материальных точек. Моментом импульса механической системы относительно точки О (начала О) называется величина (4. 11) где – момент импульса i-й материальной точки. Продифференцировав (4. 11) по времени и используя уравнение движения (4. 10), получаем (4. 12) где – сумма моментов всех сил, действующих на i-ю мат. точку. Сумму в правой части (4. 12) представим в виде двух слагаемых: (4. 13) где – сумма моментов внешних сил, действующих на систему, а – сумма моментов всех внутренних сил, действующих на все мат. точки, входящие в состав системы. Очевидно, что (4. 14)
Перейдем к описанию движения механической системы. Используем модель – набор материальных точек. Моментом импульса механической системы относительно точки О (начала О) называется величина (4. 11) где – момент импульса i-й материальной точки. Продифференцировав (4. 11) по времени и используя уравнение движения (4. 10), получаем (4. 12) где – сумма моментов всех сил, действующих на i-ю мат. точку. Сумму в правой части (4. 12) представим в виде двух слагаемых: (4. 13) где – сумма моментов внешних сил, действующих на систему, а – сумма моментов всех внутренних сил, действующих на все мат. точки, входящие в состав системы. Очевидно, что (4. 14)
 Посмотрим на тело сверху. Пусть начало координат, м. т. и лежат в плоскости рис. Внутренние для данного тела силы взаимодействия частиц действуют вдоль одной прямой.
Посмотрим на тело сверху. Пусть начало координат, м. т. и лежат в плоскости рис. Внутренние для данного тела силы взаимодействия частиц действуют вдоль одной прямой.
 Для доказательства рассмотрим взаимодействие i-й и k-й материальных точек. Силы и , которыми материальные точки действуют друг на друга, подчинены третьему закону Ньютона, (4. 15) С учетом (4. 15) получаем (4. 16) В сумму моменты внутренних сил входят парами, и для каждой пары выполняется равенство (4. 16). Отсюда следует справедливость (4. 14). Окончательно, переписываем (4. 12) в виде: (4. 17) где – сумма моментов внешних сил, действующих на систему. Уравнение (4. 15) называется уравнением вращательного движения механической системы. Его можно записать и в проекциях на координатные оси: например, для оси OZ (4. 18)
Для доказательства рассмотрим взаимодействие i-й и k-й материальных точек. Силы и , которыми материальные точки действуют друг на друга, подчинены третьему закону Ньютона, (4. 15) С учетом (4. 15) получаем (4. 16) В сумму моменты внутренних сил входят парами, и для каждой пары выполняется равенство (4. 16). Отсюда следует справедливость (4. 14). Окончательно, переписываем (4. 12) в виде: (4. 17) где – сумма моментов внешних сил, действующих на систему. Уравнение (4. 15) называется уравнением вращательного движения механической системы. Его можно записать и в проекциях на координатные оси: например, для оси OZ (4. 18)
 Основной закон динамики вращательного движения твёрдого тела. Это и есть формула основного закона вращательного движения твёрдого тела. Скорость изменения момента импульса тела относительно некоторой оси равна векторной сумме моментов внешних сил относительно этой оси, приложенных к данному телу.
Основной закон динамики вращательного движения твёрдого тела. Это и есть формула основного закона вращательного движения твёрдого тела. Скорость изменения момента импульса тела относительно некоторой оси равна векторной сумме моментов внешних сил относительно этой оси, приложенных к данному телу.
 Основной закон динамики вращательного движения твёрдого тела. Если тело абсолютно твёрдое, а ось вращение неподвижна, то момент импульса тела где I – момент инерции тела относительно рассматриваемой оси, ω – угловая скорость вращения тела. I – постоянная величина для абсолютно твёрдого тела, поэтому где ε – угловое ускорение тела. Таким образом, для абсолютно твёрдого тела, вращающегося вокруг неподвижной оси
Основной закон динамики вращательного движения твёрдого тела. Если тело абсолютно твёрдое, а ось вращение неподвижна, то момент импульса тела где I – момент инерции тела относительно рассматриваемой оси, ω – угловая скорость вращения тела. I – постоянная величина для абсолютно твёрдого тела, поэтому где ε – угловое ускорение тела. Таким образом, для абсолютно твёрдого тела, вращающегося вокруг неподвижной оси
 4. 2. Закон сохранения момента импульса. Момент инерции. Из уравнения вращательного движения системы (4. 17) непосредственно получаем закон сохранения момента импульса, (4. 19) т. е. если сумма моментов внешних сил, действующих на систему, равна нулю, то момент импульса системы сохраняется. Отметим, что здесь речь идет о векторах моментов, вычислительных относительно некоторой точки О (начала О). Это условие выполняется в случае замкнутой системы, но может выполняться и тогда, когда система не замкнута, лишь бы Рассмотрим теперь закон сохранения момента импульса относительно оси. Аналогично предыдущему, из уравнения (4. 18) получаем (4. 20) т. е. если сумма моментов действующих на систему внешних сил относительно некоторой оси равна нулю, то момент импульса системы относительно этой оси сохраняется.
4. 2. Закон сохранения момента импульса. Момент инерции. Из уравнения вращательного движения системы (4. 17) непосредственно получаем закон сохранения момента импульса, (4. 19) т. е. если сумма моментов внешних сил, действующих на систему, равна нулю, то момент импульса системы сохраняется. Отметим, что здесь речь идет о векторах моментов, вычислительных относительно некоторой точки О (начала О). Это условие выполняется в случае замкнутой системы, но может выполняться и тогда, когда система не замкнута, лишь бы Рассмотрим теперь закон сохранения момента импульса относительно оси. Аналогично предыдущему, из уравнения (4. 18) получаем (4. 20) т. е. если сумма моментов действующих на систему внешних сил относительно некоторой оси равна нулю, то момент импульса системы относительно этой оси сохраняется.
 Рассмотрим вращательное движение МТ массой по окружности радиуса с линейной скоростью. Относительно неподвижной оси вращения имеем для момента импульса: (4. 21) Введем новую величину , (4. 22) которая называется моментом инерции МТ относительно оси. Для системы МТ момент инерции может быть записан в виде (4. 6): и называется моментом инерции системы МТ относительно оси. Если тело однородно, то момент инерции может быть представлен как (4. 23) где - элемент массы, - расстояние до оси вращения. PS. Момент инерции – величина, аддитивная по определению. Для момента импульса системы МТ ( аналогично) имеем: (4. 24) Пример. Скамья Жуковского (круглая горизонтальная платформа, которая может вращаться практически без трения вокруг вертикальной оси). Проведем лекционный эксперимент!
Рассмотрим вращательное движение МТ массой по окружности радиуса с линейной скоростью. Относительно неподвижной оси вращения имеем для момента импульса: (4. 21) Введем новую величину , (4. 22) которая называется моментом инерции МТ относительно оси. Для системы МТ момент инерции может быть записан в виде (4. 6): и называется моментом инерции системы МТ относительно оси. Если тело однородно, то момент инерции может быть представлен как (4. 23) где - элемент массы, - расстояние до оси вращения. PS. Момент инерции – величина, аддитивная по определению. Для момента импульса системы МТ ( аналогично) имеем: (4. 24) Пример. Скамья Жуковского (круглая горизонтальная платформа, которая может вращаться практически без трения вокруг вертикальной оси). Проведем лекционный эксперимент!
 Закон сохранения момента импульса. Если на твёрдое тело (или систему тел) не действуют внешние моменты сил, то согласно основному закону динамики вращательного движения где - момент импульса тела (или суммарный момент импульса системы тел). Таким образом, Если на твёрдое тело (или систему тел) не действуют внешние моменты сил, то момент импульса тела (или суммарный момент импульса системы тел) остаётся неизменным. Эксперимент, иллюстрирующий действие закона сохранения момента импульса.
Закон сохранения момента импульса. Если на твёрдое тело (или систему тел) не действуют внешние моменты сил, то согласно основному закону динамики вращательного движения где - момент импульса тела (или суммарный момент импульса системы тел). Таким образом, Если на твёрдое тело (или систему тел) не действуют внешние моменты сил, то момент импульса тела (или суммарный момент импульса системы тел) остаётся неизменным. Эксперимент, иллюстрирующий действие закона сохранения момента импульса.
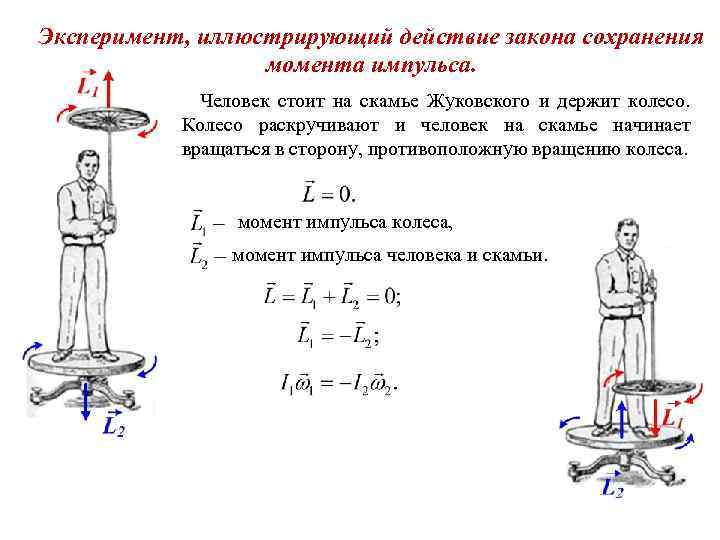
 Эксперимент, иллюстрирующий действие закона сохранения момента импульса. Человек стоит на скамье Жуковского и держит колесо. Колесо раскручивают и человек на скамье начинает вращаться в сторону, противоположную вращению колеса. момент импульса колеса, момент импульса человека и скамьи.
Эксперимент, иллюстрирующий действие закона сохранения момента импульса. Человек стоит на скамье Жуковского и держит колесо. Колесо раскручивают и человек на скамье начинает вращаться в сторону, противоположную вращению колеса. момент импульса колеса, момент импульса человека и скамьи.
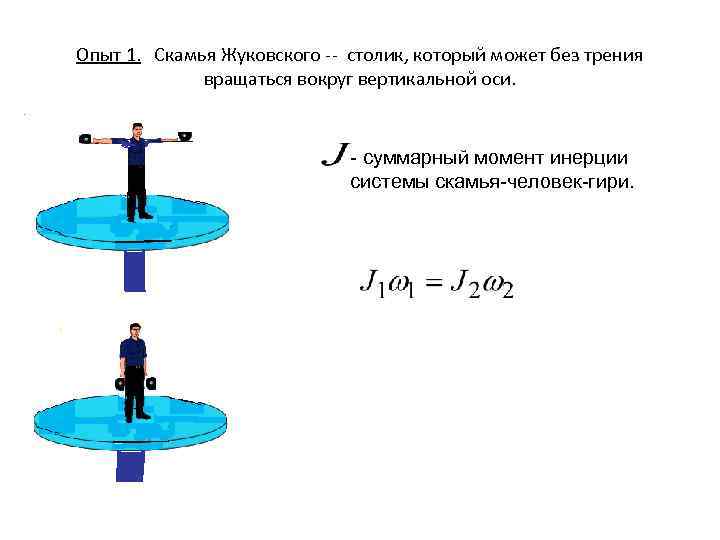
 Опыт 1. Скамья Жуковского -- столик, который может без трения вращаться вокруг вертикальной оси. - суммарный момент инерции системы скамья-человек-гири.
Опыт 1. Скамья Жуковского -- столик, который может без трения вращаться вокруг вертикальной оси. - суммарный момент инерции системы скамья-человек-гири.
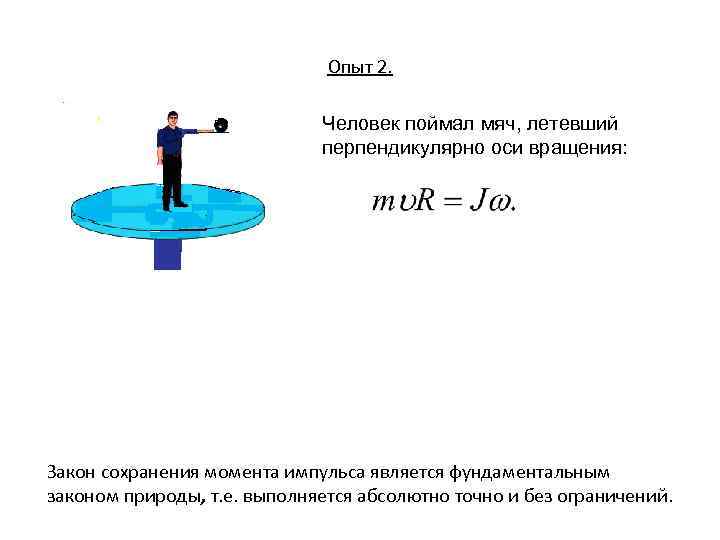
 Опыт 2. Человек поймал мяч, летевший перпендикулярно оси вращения: Закон сохранения момента импульса является фундаментальным законом природы, т. е. выполняется абсолютно точно и без ограничений.
Опыт 2. Человек поймал мяч, летевший перпендикулярно оси вращения: Закон сохранения момента импульса является фундаментальным законом природы, т. е. выполняется абсолютно точно и без ограничений.
 4. 3 Примеры вычисления моментов инерции твердых тел. Теорема Штейнера. Пример № 1. Пусть имеется тонкий однородный стержень длиной и массой. Однородность означает, что масса участка стержня пропорциональна длине этого участка. Тогда линейную плотность массы можно записать (4. 30) или ввести функцию , где – расстояние от данной точки стержня до его левого конца, которая определяется равенством: (4. 31) Однородность тонкого стержня также означает, что для всех точек стержня (4. 32) PS. По аналогии с известной вам объемной плотностью вещества можно сказать так: величина – средняя линейная плотность массы стержня, а – линейная плотность массы в точке. Рассчитаем момент инерции стержня относительно оси OO , перпендикулярной стержню и проходящей через один из его концов (рис. 4. 7).
4. 3 Примеры вычисления моментов инерции твердых тел. Теорема Штейнера. Пример № 1. Пусть имеется тонкий однородный стержень длиной и массой. Однородность означает, что масса участка стержня пропорциональна длине этого участка. Тогда линейную плотность массы можно записать (4. 30) или ввести функцию , где – расстояние от данной точки стержня до его левого конца, которая определяется равенством: (4. 31) Однородность тонкого стержня также означает, что для всех точек стержня (4. 32) PS. По аналогии с известной вам объемной плотностью вещества можно сказать так: величина – средняя линейная плотность массы стержня, а – линейная плотность массы в точке. Рассчитаем момент инерции стержня относительно оси OO , перпендикулярной стержню и проходящей через один из его концов (рис. 4. 7).
 Поскольку масса распределена вдоль стержня непрерывным образом , “размазана” по стержню, при вычислении момента инерции мы поступим так. Выделим бесконечно малый кусочек стержня (элемент) (см. рис. 4. 7) с массой (материальная точка). Найдем момент инерции этого элемента относительно оси, (4. 33) Момент инерции всего стержня: (4. 34) Величина dm выражается с помощью определения (4. 31): (4. 35) Учитывая однородность стержня, запишем (4. 36) Тогда (4. 37)
Поскольку масса распределена вдоль стержня непрерывным образом , “размазана” по стержню, при вычислении момента инерции мы поступим так. Выделим бесконечно малый кусочек стержня (элемент) (см. рис. 4. 7) с массой (материальная точка). Найдем момент инерции этого элемента относительно оси, (4. 33) Момент инерции всего стержня: (4. 34) Величина dm выражается с помощью определения (4. 31): (4. 35) Учитывая однородность стержня, запишем (4. 36) Тогда (4. 37)
 Подставляя (4. 37) в (4. 34), получаем выражение для момента инерции стержня в виде определенного интеграла: (4. 38) Понятно, что в (4. 38) суммируются вклады в моменты инерции элементов стержня, положение каждого из которых определяется величиной. (расстоянием до оси вращения), а изменяется от 0 до. Вычислив интеграл (4. 38), получим (4. 39) Пример № 2. Найдем момент инерции сплошного однородного цилиндра массы и радиуса относительно оси цилиндра. Пусть – высота цилиндра. Тогда его плотность в любой точке (4. 40) «Порежем» цилиндр на соосные трубы с бесконечно тонкими стенками. На рис. 4. 8 показаны сплошной цилиндр и одна из таких бесконечно тонких труб. Радиус трубы , толщина стенки – . Масса трубы (4. 41) где – объем трубы.
Подставляя (4. 37) в (4. 34), получаем выражение для момента инерции стержня в виде определенного интеграла: (4. 38) Понятно, что в (4. 38) суммируются вклады в моменты инерции элементов стержня, положение каждого из которых определяется величиной. (расстоянием до оси вращения), а изменяется от 0 до. Вычислив интеграл (4. 38), получим (4. 39) Пример № 2. Найдем момент инерции сплошного однородного цилиндра массы и радиуса относительно оси цилиндра. Пусть – высота цилиндра. Тогда его плотность в любой точке (4. 40) «Порежем» цилиндр на соосные трубы с бесконечно тонкими стенками. На рис. 4. 8 показаны сплошной цилиндр и одна из таких бесконечно тонких труб. Радиус трубы , толщина стенки – . Масса трубы (4. 41) где – объем трубы.
 Момент инерции трубы (4. 42) Интегрируя по от , получаем момент инерции цилиндра: (4. 43) Подставив в (4. 43) выражение для плотности цилиндра (4. 40), найдем (4. 44) PS. Отметим, что полученный результат не зависит от высоты цилиндра. Поэтому он годится и для однородного диска, в том числе и сколь угодно тонкого, а в пределе – и бесконечно тонкого.
Момент инерции трубы (4. 42) Интегрируя по от , получаем момент инерции цилиндра: (4. 43) Подставив в (4. 43) выражение для плотности цилиндра (4. 40), найдем (4. 44) PS. Отметим, что полученный результат не зависит от высоты цилиндра. Поэтому он годится и для однородного диска, в том числе и сколь угодно тонкого, а в пределе – и бесконечно тонкого.
 Рассмотрим далее важное понятие – центр масс (центр инерции). Пусть . – массы материальных точек системы, – их радиусы-векторы. Центром масс (центром инерции) механической системы называется точка, положение которой определяется радиус-вектором. (4. 45) Часто пользуются более простым (менее подробным) символом суммирования, например, массу системы записывают в виде: (4. 46) Определение (2. 6) можно записать в проекциях, тогда, например, для координаты центра масс получим (4. 47) PS 1. Определение (4. 45) можно применить и к твердому телу, рассматривая его как набор материальных точек. PS 2. Нетрудно убедиться в том, что положения центров масс симметричных систем (например, однородного шара или отрезка с равномерно распределенной массой), вычисленные по формуле (4. 45), совпадают с центром симметрии этих систем, как и должно бы быть.
Рассмотрим далее важное понятие – центр масс (центр инерции). Пусть . – массы материальных точек системы, – их радиусы-векторы. Центром масс (центром инерции) механической системы называется точка, положение которой определяется радиус-вектором. (4. 45) Часто пользуются более простым (менее подробным) символом суммирования, например, массу системы записывают в виде: (4. 46) Определение (2. 6) можно записать в проекциях, тогда, например, для координаты центра масс получим (4. 47) PS 1. Определение (4. 45) можно применить и к твердому телу, рассматривая его как набор материальных точек. PS 2. Нетрудно убедиться в том, что положения центров масс симметричных систем (например, однородного шара или отрезка с равномерно распределенной массой), вычисленные по формуле (4. 45), совпадают с центром симметрии этих систем, как и должно бы быть.
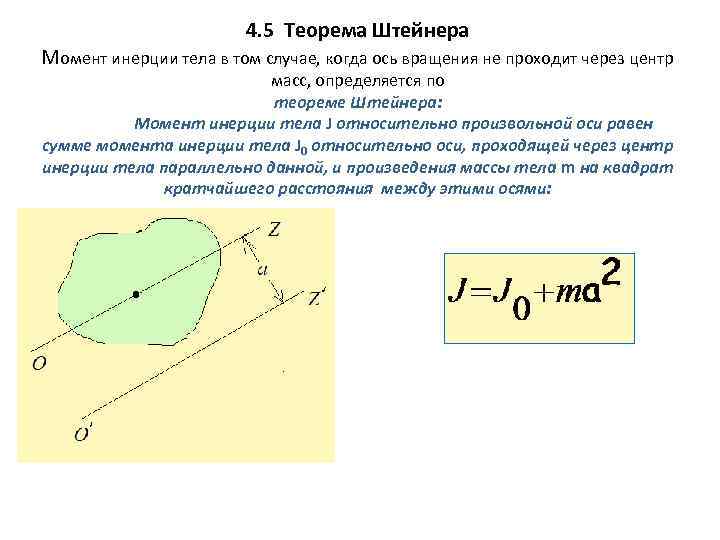
 4. 5 Теорема Штейнера Момент инерции тела в том случае, когда ось вращения не проходит через центр масс, определяется по теореме Штейнера: Момент инерции тела J относительно произвольной оси равен сумме момента инерции тела J 0 относительно оси, проходящей через центр инерции тела параллельно данной, и произведения массы тела m на квадрат кратчайшего расстояния между этими осями:
4. 5 Теорема Штейнера Момент инерции тела в том случае, когда ось вращения не проходит через центр масс, определяется по теореме Штейнера: Момент инерции тела J относительно произвольной оси равен сумме момента инерции тела J 0 относительно оси, проходящей через центр инерции тела параллельно данной, и произведения массы тела m на квадрат кратчайшего расстояния между этими осями:
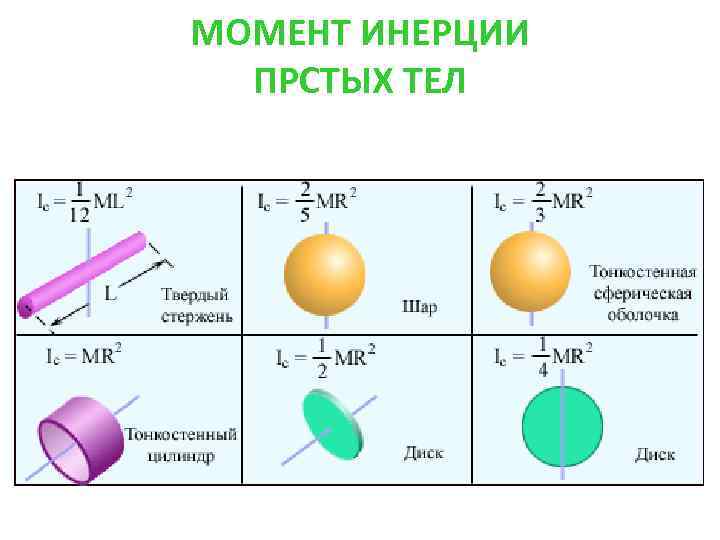
 МОМЕНТ ИНЕРЦИИ ПРСТЫХ ТЕЛ
МОМЕНТ ИНЕРЦИИ ПРСТЫХ ТЕЛ
 Применение теоремы Гюйгенса - Штейнера. Обруч подвешен в точке A (см. рисунок). Согласно теореме Гюйгенса - Штейнера Момент инерции обруча относительно центра масс Расстояние между осями, проходящими через точку A и через центр масс Окончательно, момент инерции относительно оси, проходящей через точку A
Применение теоремы Гюйгенса - Штейнера. Обруч подвешен в точке A (см. рисунок). Согласно теореме Гюйгенса - Штейнера Момент инерции обруча относительно центра масс Расстояние между осями, проходящими через точку A и через центр масс Окончательно, момент инерции относительно оси, проходящей через точку A
 Применение теоремы Гюйгенса - Штейнера. Диск закреплён на оси, проходящей через точку A, отстоящую от центра диска на половину радиуса (см. рисунок). Согласно теореме Гюйгенса - Штейнера Момент инерции диска относительно центра масс Расстояние между осями, проходящими через точку A и через центр масс Окончательно, момент инерции относительно оси, проходящей через точку A
Применение теоремы Гюйгенса - Штейнера. Диск закреплён на оси, проходящей через точку A, отстоящую от центра диска на половину радиуса (см. рисунок). Согласно теореме Гюйгенса - Штейнера Момент инерции диска относительно центра масс Расстояние между осями, проходящими через точку A и через центр масс Окончательно, момент инерции относительно оси, проходящей через точку A
 Применение теоремы Гюйгенса - Штейнера. Стержень закреплён на оси, проходящей через его крайнюю точку. Согласно теореме Гюйгенса - Штейнера Момент инерции стержня относительно центра масс, совпадающего с геометрическим центром Расстояние между осями, проходящими через точку A и через центр масс Окончательно, момент инерции относительно оси, проходящей через точку A
Применение теоремы Гюйгенса - Штейнера. Стержень закреплён на оси, проходящей через его крайнюю точку. Согласно теореме Гюйгенса - Штейнера Момент инерции стержня относительно центра масс, совпадающего с геометрическим центром Расстояние между осями, проходящими через точку A и через центр масс Окончательно, момент инерции относительно оси, проходящей через точку A
 4. 4. Кинетическая энергия вращающегося тела. Работа при вращательном движении. Теорема о кинетической энергии. При вращении тела относительно некоторой оси скорости всех его материальных точек определяются равенством (4. 60) где – угловая скорость тела, а – поперечная составляющая радиуса- вектора материальной точки . Начало отсчета О лежит на оси вращения, так что начало вектора также находится на оси. Из (4. 60) следует (4. 61) Подставляя выражение (4. 61) в определение кинетической энергии (4. 62) получаем (4. 63) Но сумма в скобках в (4. 63) – это момент инерции тела относительно оси. Поэтому для вращающегося тела окончательно имеем (4. 64)
4. 4. Кинетическая энергия вращающегося тела. Работа при вращательном движении. Теорема о кинетической энергии. При вращении тела относительно некоторой оси скорости всех его материальных точек определяются равенством (4. 60) где – угловая скорость тела, а – поперечная составляющая радиуса- вектора материальной точки . Начало отсчета О лежит на оси вращения, так что начало вектора также находится на оси. Из (4. 60) следует (4. 61) Подставляя выражение (4. 61) в определение кинетической энергии (4. 62) получаем (4. 63) Но сумма в скобках в (4. 63) – это момент инерции тела относительно оси. Поэтому для вращающегося тела окончательно имеем (4. 64)
 PS. В общем случае кинетическая энергия твердого тела может быть представлена в виде суммы (4. 65) где (4. 66) – кинетическая энергия поступательного движения тела, – масса тела, . – скорость его центра масс; (4. 67) кинетическая энергия вращения тела относительно оси, проходящей через центр масс. Таким образом, справедливость равенства (4. 68) для твердого тела доказана. Представление кинетической энергии в виде суммы (4. 68) справедливо только для твердого тела.
PS. В общем случае кинетическая энергия твердого тела может быть представлена в виде суммы (4. 65) где (4. 66) – кинетическая энергия поступательного движения тела, – масса тела, . – скорость его центра масс; (4. 67) кинетическая энергия вращения тела относительно оси, проходящей через центр масс. Таким образом, справедливость равенства (4. 68) для твердого тела доказана. Представление кинетической энергии в виде суммы (4. 68) справедливо только для твердого тела.
 Пример. Пусть имеется тонкий обруч массой и радиусом , который катится без проскальзывания по горизонтальной поверхности со скоростью . Найдем кинетическую энергию катящегося обруча. Величина – это скорость центра масс обруча. В системе отсчета, связанной с центром масс обруча, горизонтальная поверхность движется “назад” со скоростью , а обруч вращается с угловой скоростью (4. 69) Момент инерции обруча относительно оси, проходящей через его центр (совпадающий с центром масс) (4. 70) Используя формулу (4. 68), получаем (4. 71) Рассмотрим работу внешней силы , действующей на твердое тело, вращающееся вокруг закрепленной оси. Тело – набор материальных точек, и сила оказывается приложенной к какой-то материальной точке. Элементарная работа силы , по определению, (4. 72) где – бесконечно малое перемещение этой материальной точки.
Пример. Пусть имеется тонкий обруч массой и радиусом , который катится без проскальзывания по горизонтальной поверхности со скоростью . Найдем кинетическую энергию катящегося обруча. Величина – это скорость центра масс обруча. В системе отсчета, связанной с центром масс обруча, горизонтальная поверхность движется “назад” со скоростью , а обруч вращается с угловой скоростью (4. 69) Момент инерции обруча относительно оси, проходящей через его центр (совпадающий с центром масс) (4. 70) Используя формулу (4. 68), получаем (4. 71) Рассмотрим работу внешней силы , действующей на твердое тело, вращающееся вокруг закрепленной оси. Тело – набор материальных точек, и сила оказывается приложенной к какой-то материальной точке. Элементарная работа силы , по определению, (4. 72) где – бесконечно малое перемещение этой материальной точки.
 Но при вращательном движении (4. 73) где – вектор бесконечно малого поворота тела (и любой точки тела). Представив силу в виде суммы (4. 74) перепишем выражение для элементарной работы: (4. 75) Первое слагаемое в правой части (4. 75) равно нулю. Тогда (см. (4. 73)) (4. 76) Используя циклическую перестановку в смешанном произведении, получаем (4. 77) Здесь – продольная составляющая вектора момента силы относительно начала О, расположенного на оси вращения. Введем ось OZ, совместив ее с осью вращения. (4. 78) Выражение (4. 78) – работа силы при бесконечно малом повороте. Если – сумма сил, приложенных в одной точке тела, то в (4. 78) – сумма моментов этих сил относительно оси OZ. Работа силы при повороте тела на конечный угол вычисляется по формуле (4. 79) и – начальное и конечное значение координаты .
Но при вращательном движении (4. 73) где – вектор бесконечно малого поворота тела (и любой точки тела). Представив силу в виде суммы (4. 74) перепишем выражение для элементарной работы: (4. 75) Первое слагаемое в правой части (4. 75) равно нулю. Тогда (см. (4. 73)) (4. 76) Используя циклическую перестановку в смешанном произведении, получаем (4. 77) Здесь – продольная составляющая вектора момента силы относительно начала О, расположенного на оси вращения. Введем ось OZ, совместив ее с осью вращения. (4. 78) Выражение (4. 78) – работа силы при бесконечно малом повороте. Если – сумма сил, приложенных в одной точке тела, то в (4. 78) – сумма моментов этих сил относительно оси OZ. Работа силы при повороте тела на конечный угол вычисляется по формуле (4. 79) и – начальное и конечное значение координаты .
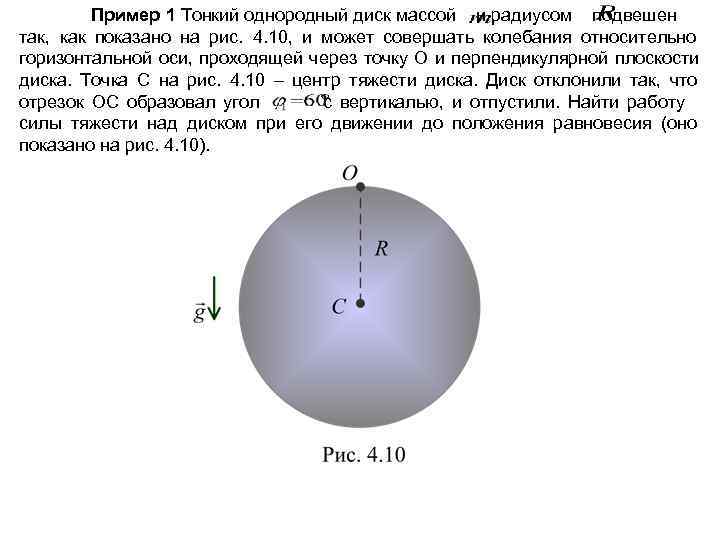
 Пример 1 Тонкий однородный диск массой и радиусом подвешен так, как показано на рис. 4. 10, и может совершать колебания относительно горизонтальной оси, проходящей через точку О и перпендикулярной плоскости диска. Точка С на рис. 4. 10 – центр тяжести диска. Диск отклонили так, что отрезок ОС образовал угол с вертикалью, и отпустили. Найти работу силы тяжести над диском при его движении до положения равновесия (оно показано на рис. 4. 10).
Пример 1 Тонкий однородный диск массой и радиусом подвешен так, как показано на рис. 4. 10, и может совершать колебания относительно горизонтальной оси, проходящей через точку О и перпендикулярной плоскости диска. Точка С на рис. 4. 10 – центр тяжести диска. Диск отклонили так, что отрезок ОС образовал угол с вертикалью, и отпустили. Найти работу силы тяжести над диском при его движении до положения равновесия (оно показано на рис. 4. 10).
 Можно считать, что сила тяжести приложена к материальной точке, содержащей центр тяжести, – точку С. . Начальное и конечное значение угловой координаты этой точки равны соответственно , см. рис. 4. 11. На рис. 4. 11 ось OZ направлена к наблюдателю. Момент силы тяжести относительно оси OZ определяется углом (см. рис. 4. 11): (4. 80) Работу вычисляем по формуле (4. 139): , (4. 81)
Можно считать, что сила тяжести приложена к материальной точке, содержащей центр тяжести, – точку С. . Начальное и конечное значение угловой координаты этой точки равны соответственно , см. рис. 4. 11. На рис. 4. 11 ось OZ направлена к наблюдателю. Момент силы тяжести относительно оси OZ определяется углом (см. рис. 4. 11): (4. 80) Работу вычисляем по формуле (4. 139): , (4. 81)
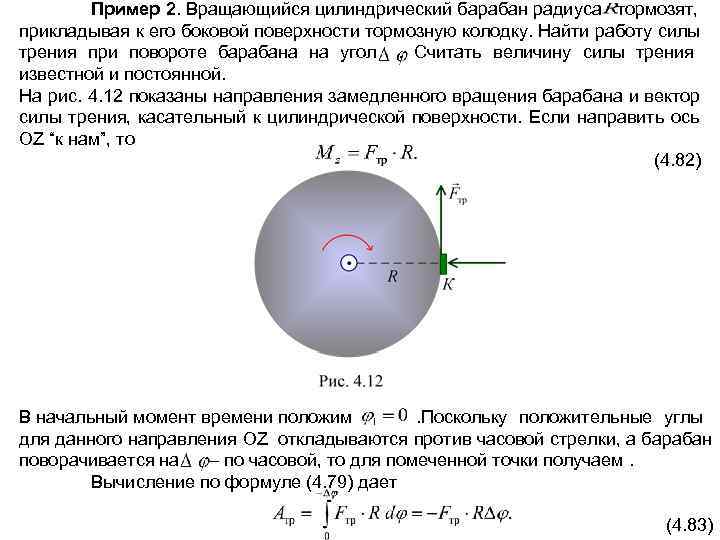
 Пример 2. Вращающийся цилиндрический барабан радиуса тормозят, прикладывая к его боковой поверхности тормозную колодку. Найти работу силы трения при повороте барабана на угол. Считать величину силы трения известной и постоянной. На рис. 4. 12 показаны направления замедленного вращения барабана и вектор силы трения, касательный к цилиндрической поверхности. Если направить ось OZ “к нам”, то (4. 82) В начальный момент времени положим . Поскольку положительные углы для данного направления OZ откладываются против часовой стрелки, а барабан поворачивается на – по часовой, то для помеченной точки получаем. Вычисление по формуле (4. 79) дает (4. 83)
Пример 2. Вращающийся цилиндрический барабан радиуса тормозят, прикладывая к его боковой поверхности тормозную колодку. Найти работу силы трения при повороте барабана на угол. Считать величину силы трения известной и постоянной. На рис. 4. 12 показаны направления замедленного вращения барабана и вектор силы трения, касательный к цилиндрической поверхности. Если направить ось OZ “к нам”, то (4. 82) В начальный момент времени положим . Поскольку положительные углы для данного направления OZ откладываются против часовой стрелки, а барабан поворачивается на – по часовой, то для помеченной точки получаем. Вычисление по формуле (4. 79) дает (4. 83)
 Теорема о кинетической энергии для вращательного движения. Элементарная работа силы, приложенной к определенной материальной точке, . . Сила - внешняя. Очевидно, что работа внутренней силы над твердым телом должна определяться точно так же – определение работы должно быть универсальным. Поскольку определение работы осталось прежним, теорема о кинетической энергии также должна сохранить свой вид: (4. 84) Левая часть (4. 84) – изменение кинетической энергии твердого тела за бесконечно малый промежуток времени , правая – алгебраическая сумма элементарных (за время ) работ всех сил, действующих на тело (т. е. на все материальные точки тела). Примененим теорему (4. 84) к случаю чисто вращательного движения твердого тела, например, к вращению тела с закрепленной осью. Действующая на вращающееся твердое тело внешняя сила “включает” внутренние силы в твердом теле. Тормозная колодка в рассмотренном выше примере действует на элементы тела, расположенные на правом конце горизонтального диаметра барабана (по рис. 4. 12), в результате чего тормозятся все элементы тела. Это – результат действия внутренних сил. Таким образом, естественно записать суммарную работу в виде (4. 85) где – сумма элементарных работ внутренних сил, а – сумма элементарных работ сил внешних.
Теорема о кинетической энергии для вращательного движения. Элементарная работа силы, приложенной к определенной материальной точке, . . Сила - внешняя. Очевидно, что работа внутренней силы над твердым телом должна определяться точно так же – определение работы должно быть универсальным. Поскольку определение работы осталось прежним, теорема о кинетической энергии также должна сохранить свой вид: (4. 84) Левая часть (4. 84) – изменение кинетической энергии твердого тела за бесконечно малый промежуток времени , правая – алгебраическая сумма элементарных (за время ) работ всех сил, действующих на тело (т. е. на все материальные точки тела). Примененим теорему (4. 84) к случаю чисто вращательного движения твердого тела, например, к вращению тела с закрепленной осью. Действующая на вращающееся твердое тело внешняя сила “включает” внутренние силы в твердом теле. Тормозная колодка в рассмотренном выше примере действует на элементы тела, расположенные на правом конце горизонтального диаметра барабана (по рис. 4. 12), в результате чего тормозятся все элементы тела. Это – результат действия внутренних сил. Таким образом, естественно записать суммарную работу в виде (4. 85) где – сумма элементарных работ внутренних сил, а – сумма элементарных работ сил внешних.
 Эти слагаемые могут быть представлены в форме (см. (4. 78)) (4. 86 а) (4. 86 б) Величина – сумма моментов внутренних сил относительно оси OZ, – сумма моментов внешних сил относительно оси. Но при выводе уравнения вращательного движения мы показали, что сумма моментов внутренних сил равна нулю ( еще раз объясним ниже !). Следовательно (4. 87 а) При повороте тела на конечный угол имеем, очевидно, (4. 87 б) Равенства (4. 87) возникают из-за того, что все точки тела совершают за любой промежуток времени одинаковые угловые перемещения. Имеется поступательный аналог: при поступательном движении системы все ее точки за совершают одинаковые перемещения , и сумма работ внутренних сил оказывается равной нулю благодаря третьему закону Ньютона. Теорема о кинетической энергии, таким образом, приобретает вид (4. 88) и, соответственно, для поворотов на конечные углы (4. 89)
Эти слагаемые могут быть представлены в форме (см. (4. 78)) (4. 86 а) (4. 86 б) Величина – сумма моментов внутренних сил относительно оси OZ, – сумма моментов внешних сил относительно оси. Но при выводе уравнения вращательного движения мы показали, что сумма моментов внутренних сил равна нулю ( еще раз объясним ниже !). Следовательно (4. 87 а) При повороте тела на конечный угол имеем, очевидно, (4. 87 б) Равенства (4. 87) возникают из-за того, что все точки тела совершают за любой промежуток времени одинаковые угловые перемещения. Имеется поступательный аналог: при поступательном движении системы все ее точки за совершают одинаковые перемещения , и сумма работ внутренних сил оказывается равной нулю благодаря третьему закону Ньютона. Теорема о кинетической энергии, таким образом, приобретает вид (4. 88) и, соответственно, для поворотов на конечные углы (4. 89)
 Составим таблицу соответствия для динамических величин, характеризующих поступательное и вращательное движения (для кинематических величин таблицу соответствия мы уже составляли в лекц № 1). Для вращательного движения это момент инерции , момент импульса , момент силы и проекции этих векторов Перечисленные величины аналогичны массе , импульсу , силе и проекциям соответственно. Таблица 2 Поступат. движение Вращат. движение В уравнении поступательного движения системы (4. 90) сделаем замены . Получается уравнение вращатель движения системы (4. 91) Любому уравнению поступательного движения можно подобрать пару – аналогичное уравнение вращательного движения.
Составим таблицу соответствия для динамических величин, характеризующих поступательное и вращательное движения (для кинематических величин таблицу соответствия мы уже составляли в лекц № 1). Для вращательного движения это момент инерции , момент импульса , момент силы и проекции этих векторов Перечисленные величины аналогичны массе , импульсу , силе и проекциям соответственно. Таблица 2 Поступат. движение Вращат. движение В уравнении поступательного движения системы (4. 90) сделаем замены . Получается уравнение вращатель движения системы (4. 91) Любому уравнению поступательного движения можно подобрать пару – аналогичное уравнение вращательного движения.
 4. 5 Гироскоп. Угловая скорость прецессии. Гироскоп – это быстро вращающееся массивное тело. Примером гироскопа является хорошо известный вам с детства волчок. Гироскоп обладает очень интересным свойством, которое состоит в том, что попытка изменить ориентацию оси вращения приводит к тому, что ось гироскопа начинает вращаться. Такое вращение называется прецессией. На рис. 4. 13 показан вращающийся волчок. Будем считать, что он закреплен в точке О; – угловая скорость вращения гироскопа. В момент, когда сделан рис. 4. 13, ось гироскопа лежит в плоскости чертежа, С – центр тяжести волчка, радиус-вектор центра тяжести, проведенный из точки О. На рис. 4. 14 показаны вектор момента импульса волчка. относительно точки О, продольная (по отношению к вектору ) и поперечная его составляющие и. Рис. 4. 13 и 4. 14 соответствуют одному и тому же моменту времени, векторы , , лежат в плоскости чертежа.
4. 5 Гироскоп. Угловая скорость прецессии. Гироскоп – это быстро вращающееся массивное тело. Примером гироскопа является хорошо известный вам с детства волчок. Гироскоп обладает очень интересным свойством, которое состоит в том, что попытка изменить ориентацию оси вращения приводит к тому, что ось гироскопа начинает вращаться. Такое вращение называется прецессией. На рис. 4. 13 показан вращающийся волчок. Будем считать, что он закреплен в точке О; – угловая скорость вращения гироскопа. В момент, когда сделан рис. 4. 13, ось гироскопа лежит в плоскости чертежа, С – центр тяжести волчка, радиус-вектор центра тяжести, проведенный из точки О. На рис. 4. 14 показаны вектор момента импульса волчка. относительно точки О, продольная (по отношению к вектору ) и поперечная его составляющие и. Рис. 4. 13 и 4. 14 соответствуют одному и тому же моменту времени, векторы , , лежат в плоскости чертежа.
 Пренебрегая моментом сил трения, уравнение движения волчка запишем в виде, (4. 92) где (4. 93) – момент силы тяжести относительно т. О. Вектор . направлен “от нас” – как показано на рис. 4. 14. Бесконечно малое изменение момента импульса волчка (за время ) – (4. 94) – это вектор, также направленный “от нас”. Таким образом, получаем (4. 95 а, б) причем (4. 96) Отсюда следует (4. 97 а, б)
Пренебрегая моментом сил трения, уравнение движения волчка запишем в виде, (4. 92) где (4. 93) – момент силы тяжести относительно т. О. Вектор . направлен “от нас” – как показано на рис. 4. 14. Бесконечно малое изменение момента импульса волчка (за время ) – (4. 94) – это вектор, также направленный “от нас”. Таким образом, получаем (4. 95 а, б) причем (4. 96) Отсюда следует (4. 97 а, б)
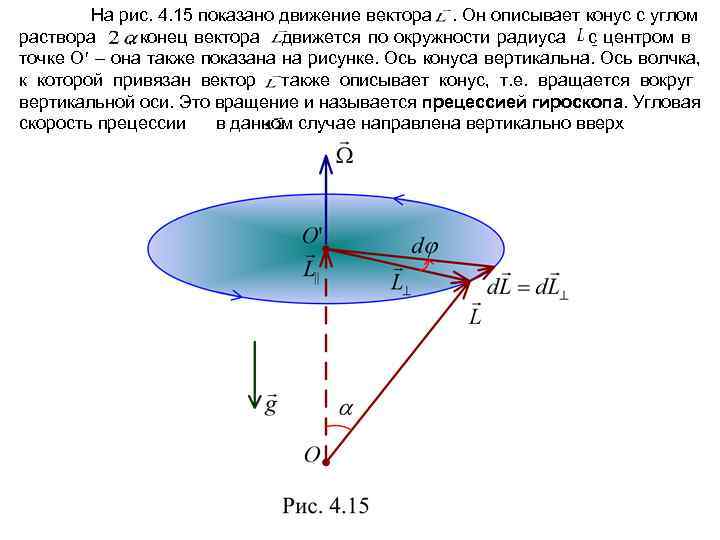
 На рис. 4. 15 показано движение вектора. Он описывает конус с углом раствора , конец вектора движется по окружности радиуса с центром в точке О – она также показана на рисунке. Ось конуса вертикальна. Ось волчка, к которой привязан вектор также описывает конус, т. е. вращается вокруг вертикальной оси. Это вращение и называется прецессией гироскопа. Угловая скорость прецессии в данном случае направлена вертикально вверх
На рис. 4. 15 показано движение вектора. Он описывает конус с углом раствора , конец вектора движется по окружности радиуса с центром в точке О – она также показана на рисунке. Ось конуса вертикальна. Ось волчка, к которой привязан вектор также описывает конус, т. е. вращается вокруг вертикальной оси. Это вращение и называется прецессией гироскопа. Угловая скорость прецессии в данном случае направлена вертикально вверх
 Величину можно вычислить как угловую скорость движения конца вектора по окружности радиуса. Очевидно (см. рис. 4. 15), (4. 98) Рассматривая бесконечно малый сектор, показанный на рис. 4. 15, мы можем записать: (4. 99) Отсюда (4. 100) Используя рис. 4. 14, получаем (4. 101 а) (4. 101 б) где . Подставляя (4. 101 а), (4. 101 б) в (4. 100), находим угловую скорость прецессии волчка (4. 102) Если – момент инерции волчка относительно его оси, то (4. 103) Отметим, что не зависит от угла между осью гироскопа и вертикалью. Применения гироскопов многочисленны и интересны. Рекомендую ознакомиться с применением гироскопов самостоятельно (по учебникам).
Величину можно вычислить как угловую скорость движения конца вектора по окружности радиуса. Очевидно (см. рис. 4. 15), (4. 98) Рассматривая бесконечно малый сектор, показанный на рис. 4. 15, мы можем записать: (4. 99) Отсюда (4. 100) Используя рис. 4. 14, получаем (4. 101 а) (4. 101 б) где . Подставляя (4. 101 а), (4. 101 б) в (4. 100), находим угловую скорость прецессии волчка (4. 102) Если – момент инерции волчка относительно его оси, то (4. 103) Отметим, что не зависит от угла между осью гироскопа и вертикалью. Применения гироскопов многочисленны и интересны. Рекомендую ознакомиться с применением гироскопов самостоятельно (по учебникам).
 § 4. ГИРОСКОПЫ Гироскопом (или волчком) называется массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии (оси гироскопа).
§ 4. ГИРОСКОПЫ Гироскопом (или волчком) называется массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии (оси гироскопа).
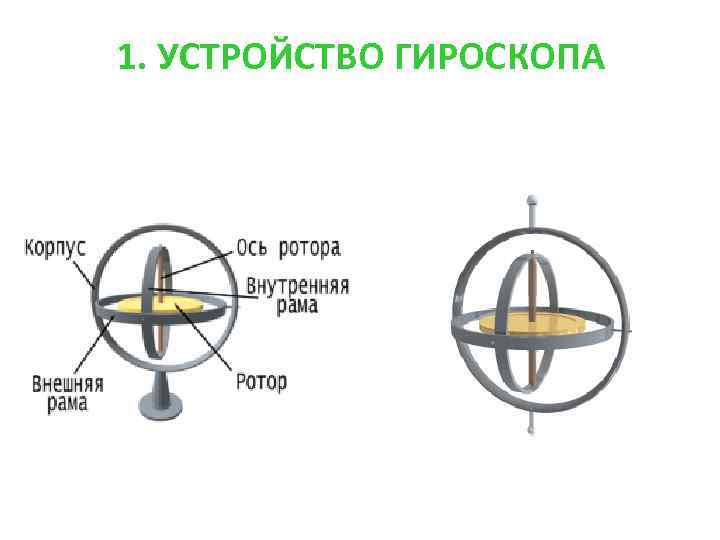
 1. УСТРОЙСТВО ГИРОСКОПА
1. УСТРОЙСТВО ГИРОСКОПА
 2. ГИРОСКОПИЧЕСКИЙ ЭФФЕКТ Гироскопический эффект состоит в том, что под действием внешней силы, перпендикулярной моменту импульса, ось гироскопа поворачивается в плоскости, содержащей момент импульса гироскопа и момент внешней силы ( перпендикулярной моменту импульса и силе).
2. ГИРОСКОПИЧЕСКИЙ ЭФФЕКТ Гироскопический эффект состоит в том, что под действием внешней силы, перпендикулярной моменту импульса, ось гироскопа поворачивается в плоскости, содержащей момент импульса гироскопа и момент внешней силы ( перпендикулярной моменту импульса и силе).
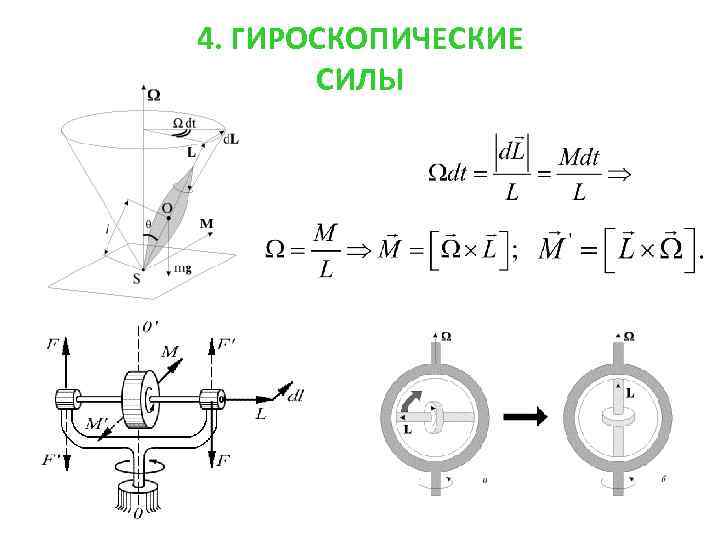
 4. ГИРОСКОПИЧЕСКИЕ СИЛЫ
4. ГИРОСКОПИЧЕСКИЕ СИЛЫ
 5. ГИРОКОМПАС Гироскопическим компасом (гирокомпасом) называется гироскоп, ось которого может свободно поворачиваться в горизонтальной плоскостипод влиянием суточного Вращения Земли.
5. ГИРОКОМПАС Гироскопическим компасом (гирокомпасом) называется гироскоп, ось которого может свободно поворачиваться в горизонтальной плоскостипод влиянием суточного Вращения Земли.
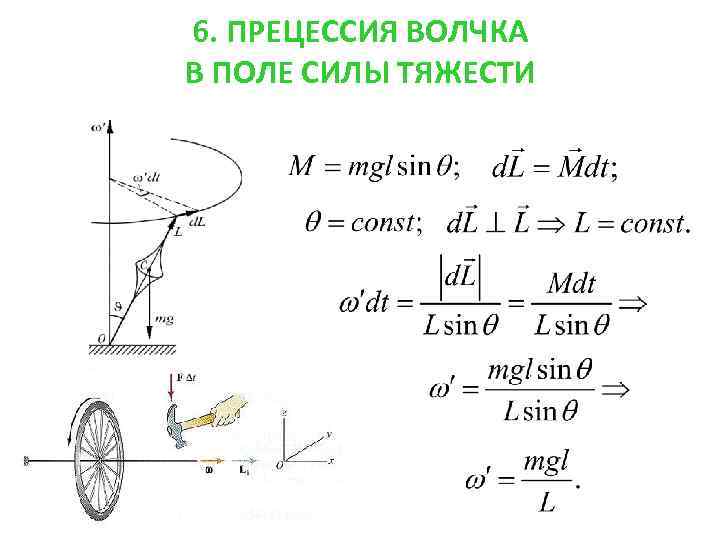
 6. ПРЕЦЕССИЯ ВОЛЧКА В ПОЛЕ СИЛЫ ТЯЖЕСТИ
6. ПРЕЦЕССИЯ ВОЛЧКА В ПОЛЕ СИЛЫ ТЯЖЕСТИ

