LEDAS Solutions for Mechanical System Modeling and Related

LEDAS Solutions for Mechanical System Modeling and Related Problems Egor Ermolin (LEDAS) SBRAS/ Intel Geometry. Seminar 10 April 2008

Agenda LEDAS Company LEDAS Phoenix and Related Projects: – History Mechanical simulation engine – Functionality – Architecture: Dynamic Engine, Collision Detection, Collision Resolution Impulse-based Collision Resolution Geometry: – Calculation of Dynamic Properties – Effective Collision Detection – Narrowing broad phase Demos Key Features Development Perspective SBRAS/ Intel Geometry. Seminar 10 April 2008 2

LEDAS Company Positioning Mission Competence Customers Isicad-2008 SBRAS/ Intel Geometry. Seminar 10 April 2008 3

Positioning of LEDAS Ltd. is an independent software development company founded in 1999 in Novosibirsk, Russia Using proprietary mathematical technologies, LEDAS provides computational components and services for software development companies in the fields of PLM (including CAD, CAM, CAE, PDM) and ERP The company also provides services for manufacturers: – Custom application development, integration & localization – Creation of 3 D models using different CAD systems – Consulting, reselling, trainings Information on LEDAS is available at www. ledas. com SBRAS/ Intel Geometry. Seminar 10 April 2008 4

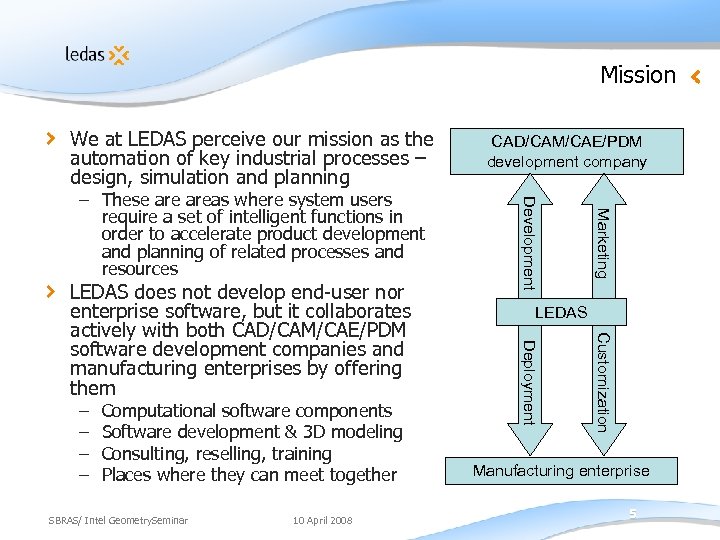Mission We at LEDAS perceive our mission as the automation of key industrial processes – design, simulation and planning SBRAS/ Intel Geometry. Seminar 10 April 2008 Customization Computational software components Software development & 3 D modeling Consulting, reselling, training Places where they can meet together Marketing – – LEDAS Deployment LEDAS does not develop end-user nor enterprise software, but it collaborates actively with both CAD/CAM/CAE/PDM software development companies and manufacturing enterprises by offering them Development – These areas where system users require a set of intelligent functions in order to accelerate product development and planning of related processes and resources CAD/CAM/CAE/PDM development company Manufacturing enterprise 5

LEDAS Competence Mathematics & Computer Science – – Numerical analysis Constraint satisfaction Computational geometry Scheduling algorithms Software Development – – – Development Processes Quality Assurance Available platforms Programming skills Software tools SBRAS/ Intel Geometry. Seminar 10 April 2008 CAD/CAM/CAE/PDM skills – Creation of 3 D models – Custom application development – Translation & localization – Certified training – Reselling – Consulting Publishing & Conferencing – Web sites – Books – Conferences 6

LEDAS Customers Dassault Systèmes (France) – Development of core computational components for CATIA V 5 products – Software localization for Russian market – Total cost of development projects is about 80 person-years since 1999 Sukhoi Civil Aircrafts (Russia), AVTOVAZ (Russia), and others – Consulting & training on CATIA/CAA solutions – Custom software development (add-on applications for CATIA and NX) in the field of computational geometry, data translation and CAD application integration Proficiency (Israel), ADEM Technologies (Russia), AWV (Switzerland), Tecnos (Italy), Evo. Solutions (Japan), and others – Licensees of LEDAS Geometric Solver (LGS) software components – Cooperation on integration of LGS into different CAD applications: sketcher, assembly design, data translation Exigen (USA), CTRUE (Israel), and others – Development of advanced software packages based on LEDAS competence in optimization algorithms, resource scheduling, and computational geometry Virtual. CAD (Canada) – Creation of libraries of parametric 3 D models and web-catalogues of CAD parts Purdue Unviversity (USA), Novosibirsk Technical University (Russia) – Education & research SBRAS/ Intel Geometry. Seminar 10 April 2008 7

Isicad-2008 Third international multi-vendor PLM forum – June 4 -6, Novosibirsk, Russia About 500 attendees representing large, medium and small manufacturing enterprises More than 30 CAD, CAM, CAE, PDM solution providers – Autodesk, Siemens PLM, PTC and Dassault are traditional participants – All leading Russian CAD/PLM R&D companies Leading Russian mass media Multi-format – – – Invited talks Plenary session talks Technical section talks Company’s seminar Round table and press conference Rich social program More information at http: //isicad. ru/2008 SBRAS/ Intel Geometry. Seminar 10 April 2008 8

We are here LEDAS Company LEDAS Phoenix and Related Projects: – History Mechanical simulation engine – Functionality – Architecture: Dynamic Engine, Collision Detection, Collision Resolution Impulse-based Collision Resolution Geometry: – Calculation of Dynamic Properties – Effective Collision Detection – Narrowing broad phase Demos Key Features Development Perspective SBRAS/ Intel Geometry. Seminar 10 April 2008 9

The Phoenix Project The LEDAS Phoenix Project is oriented to a creation of competitive mechanical simulation engine with broad spectrum of applications 2003 2 D prototype was implemented. Segments and circular arcs were used for a geometrical representation. Gravity, springs, user-defined forces, sliding friction. Collision detection and resolution. 2004 A full-scale 3 D engine is under development. Simple 3 D Collision detection. Scalable architecture 2005 3 D Collision Detection is implemented 2007 Convex Hull 3 D and Minimal Bounding Box algorithms are implemented SBRAS/ Intel Geometry. Seminar 10 April 2008 10

A Mechanical Simulation Engine Modeling of 2 D/3 D rigid bodies motion according to physical laws Modeling of forces with different nature – Gravity – Springs – Dynamically acting user-defined forces Collision detection and resolution – Avoiding interpenetration Motion modeling under geometrical constraints – Assembly constraints SBRAS/ Intel Geometry. Seminar 10 April 2008 11

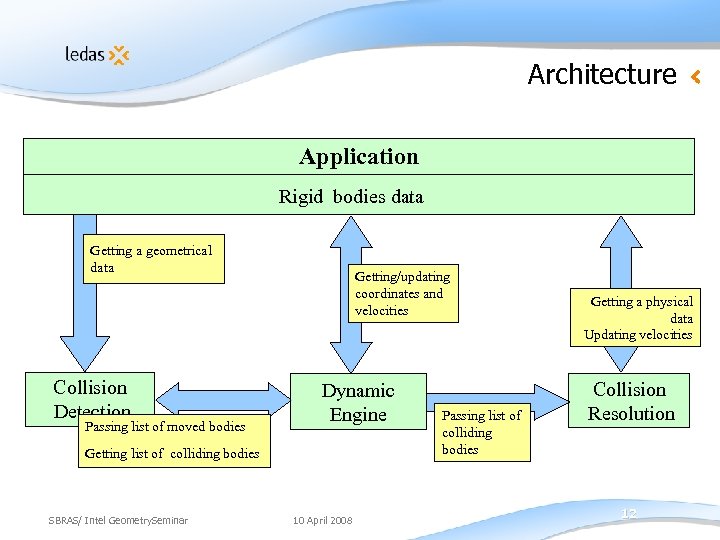Architecture Application Rigid bodies data Getting a geometrical data Collision Detection Passing list of moved bodies Getting/updating coordinates and velocities Dynamic Engine Getting list of colliding bodies SBRAS/ Intel Geometry. Seminar 10 April 2008 Passing list of colliding bodies Getting a physical data Updating velocities Collision Resolution 12

Dynamic Engine ü Models motion of rigid bodies with account of external forces • Gravity • Springs • Dynamically acting user-defined forces ü Uses simple explicit difference scheme ü Manages Collision Detection and Collision Resolution modules SBRAS/ Intel Geometry. Seminar 10 April 2008 13

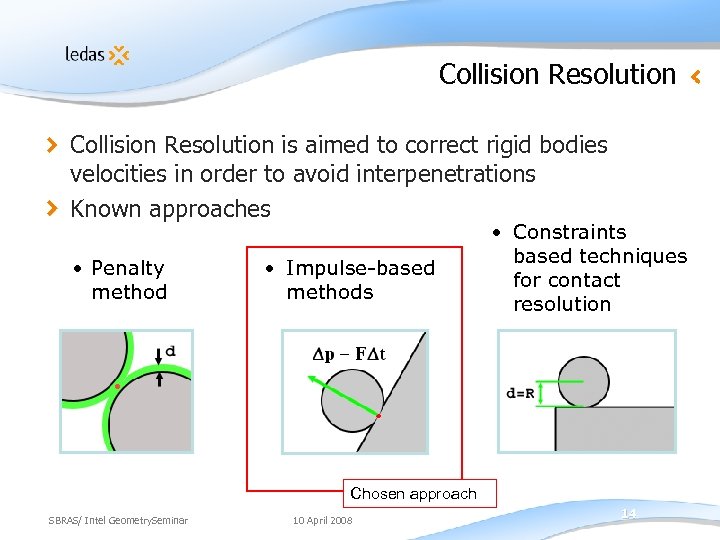Collision Resolution is aimed to correct rigid bodies velocities in order to avoid interpenetrations Known approaches • Penalty method • Impulse-based methods • Constraints based techniques for contact resolution Chosen approach SBRAS/ Intel Geometry. Seminar 10 April 2008 14

Impulse-based approach Initial assumptions Basic assumptions – Collision time is infinitely small – Collision forces are infinitely large – Increments of impulses are finite There are two phases of collision – Compression phase – Restitution phase Total impulse obtained by a body during collision takes into account both phases: where is a coefficient of restitution, and impulse obtained during compression phase SBRAS/ Intel Geometry. Seminar 10 April 2008 15

Some definitions Relative velocity at the point is calculated from first body to second: ü Normal at collision point is taken from first body ü Case scalar product : < 0 interpenetration point = 0 contact point > 0 leaving point SBRAS/ Intel Geometry. Seminar 10 April 2008 16

Approach Overview ü Consider contact points with negative normal relative velocities, such that bodies are penetrating ü Assume that force acts in contact point ü Express velocities of the bodies after a compression phase via unknown compression impulses ü With known expressions for velocities express relative normal velocities of the bodies in the contact point SBRAS/ Intel Geometry. Seminar 10 April 2008 17

Impulse-based approach Linear system ü Condition of vanishing of the relative normal velocities at the end of the compression phase leads to the following linear mxm system of equations ü We can obtain compression impulses via SVD-method and full impulses passed between bodies due to collision in i-th point is ü After determination of the impulses we can compute new velocities of the bodies SBRAS/ Intel Geometry. Seminar 10 April 2008 18

Impulse-based approach Iterative scheme With known new velocities we should check other contact points for which initially no penetration occurred If there are points in which the bodies are penetrating we repeat impulses computation for these new set of points As practice showed this iterations are converged for e≤ 1 SBRAS/ Intel Geometry. Seminar 10 April 2008 19

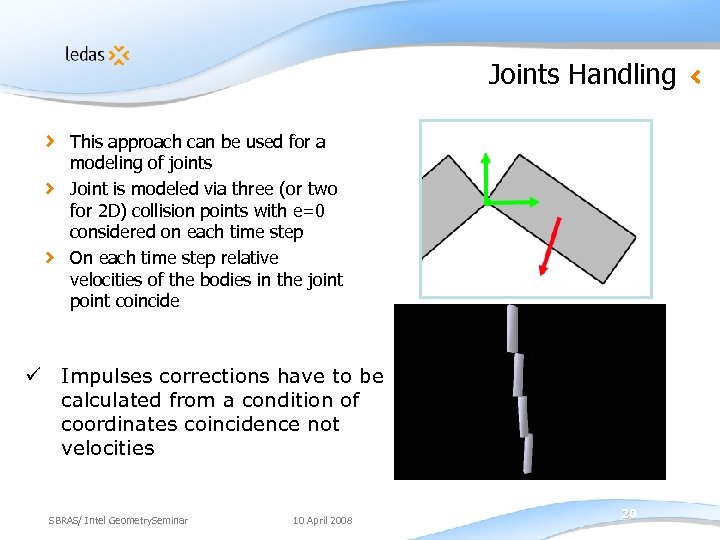Joints Handling This approach can be used for a modeling of joints Joint is modeled via three (or two for 2 D) collision points with e=0 considered on each time step On each time step relative velocities of the bodies in the joint point coincide ü Impulses corrections have to be calculated from a condition of coordinates coincidence not velocities SBRAS/ Intel Geometry. Seminar 10 April 2008 20

We are here LEDAS Company LEDAS Phoenix and Related Projects: – History Mechanical simulation engine – Functionality and applications – Architecture: Dynamic Engine, Collision Detection, Collision Resolution Impulse-based Collision Resolution Geometry: – Calculation of Dynamic Properties – Effective Collision Detection – Narrowing broad phase Demos Key Features Development Perspective SBRAS/ Intel Geometry. Seminar 10 April 2008 21

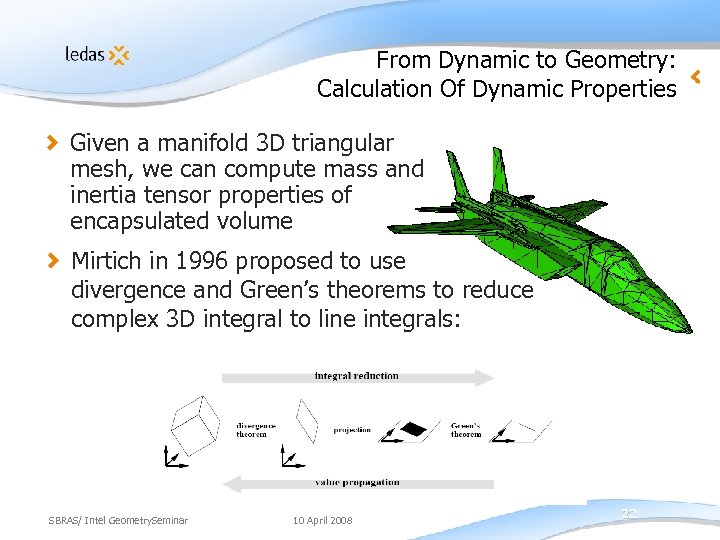From Dynamic to Geometry: Calculation Of Dynamic Properties Given a manifold 3 D triangular mesh, we can compute mass and inertia tensor properties of encapsulated volume Mirtich in 1996 proposed to use divergence and Green’s theorems to reduce complex 3 D integral to line integrals: SBRAS/ Intel Geometry. Seminar 10 April 2008 22

Collision Detection Broad phase: test collision for only for bodies which have bounding primitives intersecting Solution: encapsulate objects by simple shells with inexpensive intersection test Optimization of this phase: don’t check intersection for shells that obviously don’t intersect (rule? ) In 2 D prototype implementation we use pair-wise check on broad phase using circles as bounding primitives SBRAS/ Intel Geometry. Seminar 10 April 2008 23

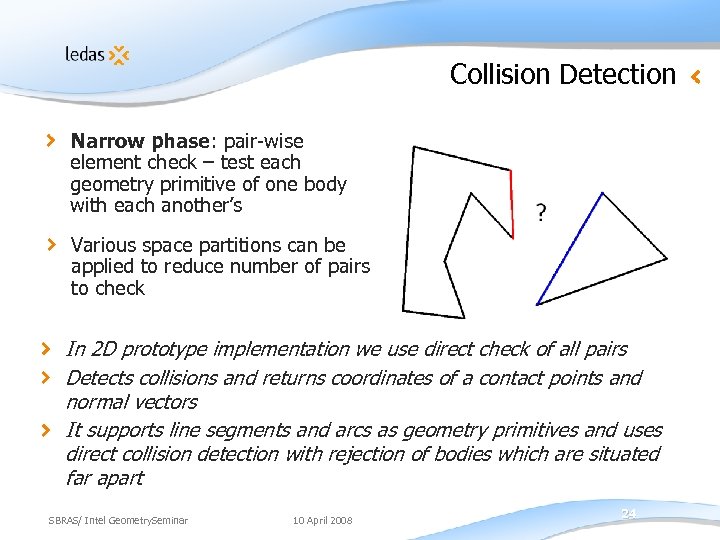Collision Detection Narrow phase: pair-wise element check – test each geometry primitive of one body with each another’s Various space partitions can be applied to reduce number of pairs to check In 2 D prototype implementation we use direct check of all pairs Detects collisions and returns coordinates of a contact points and normal vectors It supports line segments and arcs as geometry primitives and uses direct collision detection with rejection of bodies which are situated far apart SBRAS/ Intel Geometry. Seminar 10 April 2008 24

Collision Detection 3 D Implementation Based on OBB-approach (inertia axis) in narrow phase, collision detection library OPCODE 1. 3 is used for reference. Current implementation consumes less memory than OPCODE (about 10%), but is 1. 7 times slower*. However, performance optimization was not the objective Broad phase uses O(n 2) pairwise OBB-comparison. This stage can be optimized up-to O(nlogn) comparison (in practice O(n)), but even this is not top of highperformance… * Data is based on LEDAS collision detection report (in Russian) SBRAS/ Intel Geometry. Seminar 10 April 2008 25

Collision Detection: narrowing broad phase The problem is that OBB is usually better heuristics of bounding volume than AABB (in terms of volume), but it is not minimal bounding box for body in general case Which pattern better fits the broken window? AABB OBB Minimal BB The advantage is obvious: the less volume BB has, the less number of false narrow phase triggering will happen SBRAS/ Intel Geometry. Seminar 10 April 2008 26

Finding Minimal Boxes: LEDAS Implementations 2 D case only requires body to be convex, algorithm is quite straightforward and can be described by “rotating calipers” model 3 D case also operates on convex mesh and involves Gaussian sphere structure to test configuration. It requires polynomial trigonometric equation solver to find minimum of volume function SBRAS/ Intel Geometry. Seminar 10 April 2008 27

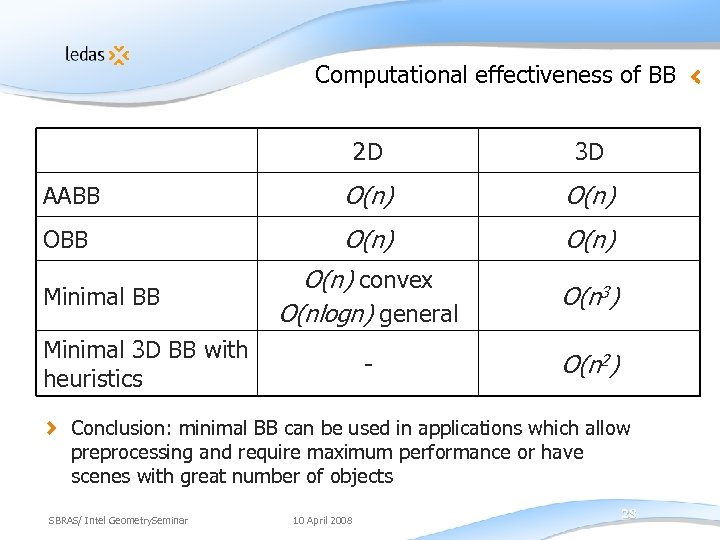Computational effectiveness of BB 2 D 3 D AABB O(n) O(n) convex O(nlogn) general O(n 3) - O(n 2) Minimal BB Minimal 3 D BB with heuristics Conclusion: minimal BB can be used in applications which allow preprocessing and require maximum performance or have scenes with great number of objects SBRAS/ Intel Geometry. Seminar 10 April 2008 28

We are here LEDAS Company LEDAS Phoenix and Related Projects: – History Mechanical simulation engine – Functionality and applications – Architecture: Dynamic Engine, Collision Detection, Collision Resolution Impulse-based Collision Resolution Geometry: – Calculation of Dynamic Properties – Effective Collision Detection – Narrowing broad phase Demos Key Features Development Perspective SBRAS/ Intel Geometry. Seminar 10 April 2008 29

Demos Unstable stack SBRAS/ Intel Geometry. Seminar 10 April 2008 30

Demos Domino effect SBRAS/ Intel Geometry. Seminar 10 April 2008 31

Demos Springs SBRAS/ Intel Geometry. Seminar 10 April 2008 32

Demos Telescopic mast SBRAS/ Intel Geometry. Seminar 10 April 2008 33

Demos Door latch SBRAS/ Intel Geometry. Seminar 10 April 2008 34

Demos Engine SBRAS/ Intel Geometry. Seminar 10 April 2008 35

Demos Jib SBRAS/ Intel Geometry. Seminar 10 April 2008 36

Demos 3 D Collision SBRAS/ Intel Geometry. Seminar 10 April 2008 37

Industrial Application Integration of Minimal Bound Box solution into CATIA (customer SCAC) is in process At LEDAS convergence of BB code is performed SBRAS/ Intel Geometry. Seminar 10 April 2008 38

We are here LEDAS Company LEDAS Phoenix and Related Projects: – History Mechanical simulation engine – Functionality and applications – Architecture: Dynamic Engine, Collision Detection, Collision Resolution Impulse-based Collision Resolution Geometry: – Calculation of Dynamic Properties – Effective Collision Detection – Narrowing broad phase Demos Key Features Development Perspective SBRAS/ Intel Geometry. Seminar 10 April 2008 39

Key Features of Phoenix Project Approach doesn’t need decomposition of bodies into convex parts Absolute elastic (energy-preserving) and inelastic adjustability Native support of geometrical constraints Collision detection in 3 D with near-industrial characteristics is ready If preprocessing allowed, bounding volumes can be very tight SBRAS/ Intel Geometry. Seminar 10 April 2008 40

Implementation Summary 2 D dynamic engine with segment-arc geometry, resolves collision, supports springs and joints Computation of mass and inertia properties for triangular mesh 3 D dynamic engine based on triangular meshes OBB collision detection 3 D convex hull module (Preparata’s divide-andconquer) Module for calculating minimal bounding box for triangle mesh SBRAS/ Intel Geometry. Seminar 10 April 2008 41

Development Perspective We have advanced results in mechanical modeling and computational geometry related problems Some of our implementations already have applications, but our solutions have much greater potential Thus we are looking for partner/customer to bring our ideas to life SBRAS/ Intel Geometry. Seminar 10 April 2008 42