Lectures 2 Thess lectures introductory aspects related to

Lectures 2 Thess lectures introductory aspects related to: - Serial vs. parallel manufacturing - Top-down vs. bottom up manufacturing - Dominant forces at microscale - Physical laws governing the evolution of microsystems - Scaling effects Dan O. Popa, EE 5349 Microsystems, Summer 2015

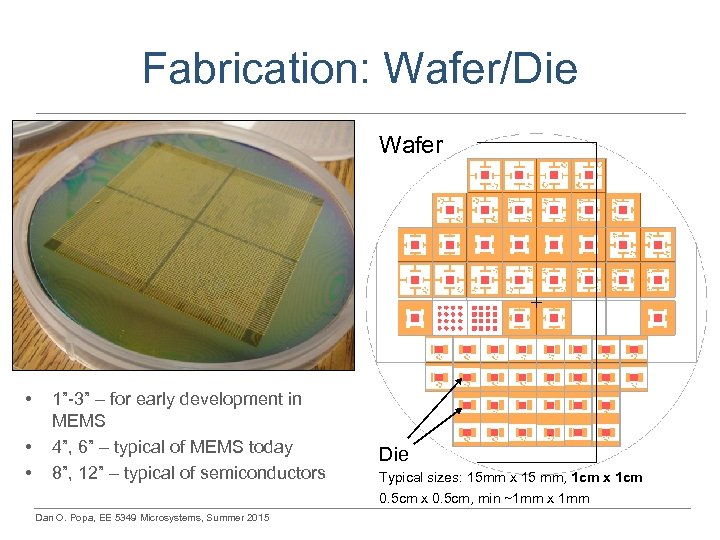Fabrication: Wafer/Die Wafer • • • 1”-3” – for early development in MEMS 4”, 6” – typical of MEMS today 8”, 12” – typical of semiconductors Dan O. Popa, EE 5349 Microsystems, Summer 2015 Die Typical sizes: 15 mm x 15 mm, 1 cm x 1 cm 0. 5 cm x 0. 5 cm, min ~1 mm x 1 mm

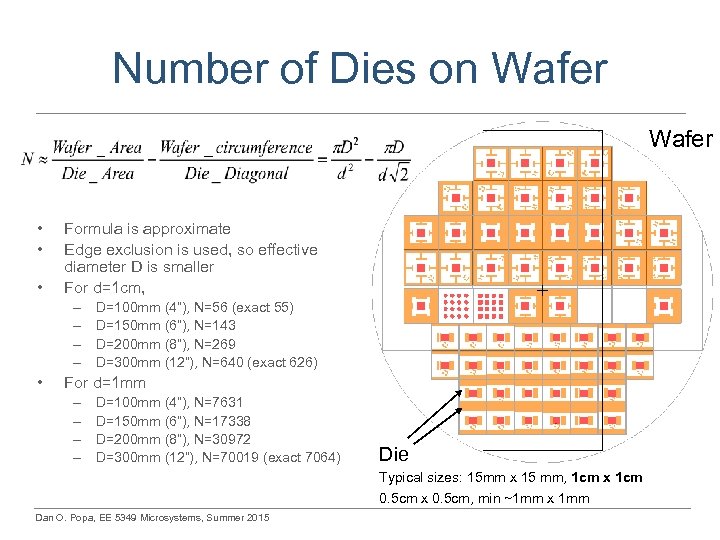Number of Dies on Wafer • • • Formula is approximate Edge exclusion is used, so effective diameter D is smaller For d=1 cm, – – • D=100 mm (4”), N=56 (exact 55) D=150 mm (6”), N=143 D=200 mm (8”), N=269 D=300 mm (12”), N=640 (exact 626) For d=1 mm – – D=100 mm (4”), N=7631 D=150 mm (6”), N=17338 D=200 mm (8”), N=30972 D=300 mm (12”), N=70019 (exact 7064) Die Typical sizes: 15 mm x 15 mm, 1 cm x 1 cm 0. 5 cm x 0. 5 cm, min ~1 mm x 1 mm Dan O. Popa, EE 5349 Microsystems, Summer 2015

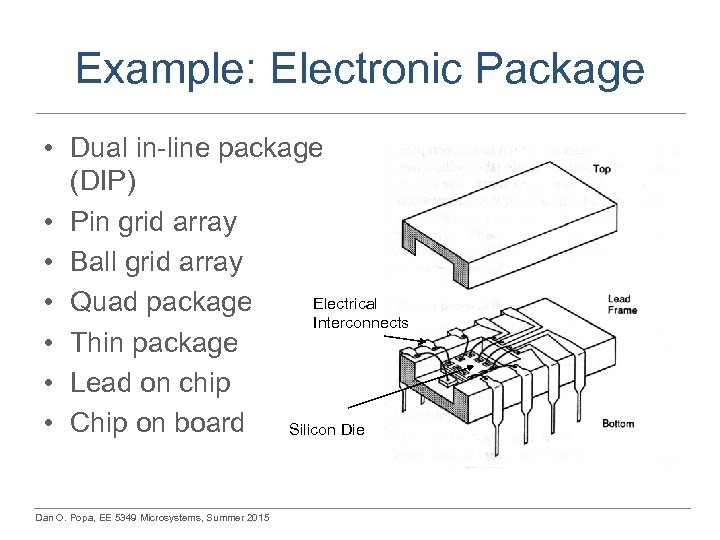Example: Electronic Package • Dual in-line package (DIP) • Pin grid array • Ball grid array Electrical • Quad package Interconnects • Thin package • Lead on chip • Chip on board Silicon Die Dan O. Popa, EE 5349 Microsystems, Summer 2015

Manufacturing Process (example) Process Example of outcome Micromachining Silicon wafer Dicing Silicon die Molding etc. Metal / plastic house Packaging System Testing High Yield Systems integration Product Die accounts for only ~ 10 -70% of system cost Concurrent development required Dan O. Popa, EE 5349 Microsystems, Summer 2015

Serial vs. Parallel Manufacturing Serial Manufacturing • • • Manufacturing devices one by one Requires high speed Requires space (expensive in a clean room) Sensitive to equipment failures (if all products pass through processor A and it fails, production will stop) Tool changes create delays Main advantage: high production flexibility Parallel Manufacturing • • Manufacturing devices in batches Example: Wafer level Requires high yield Requires removal of failures (“Known Good Die problem”) Requires singulation at some point to make individual devices Requires more expensive tooling Main advantage: high production volume Dan O. Popa, EE 5349 Microsystems, Summer 2015

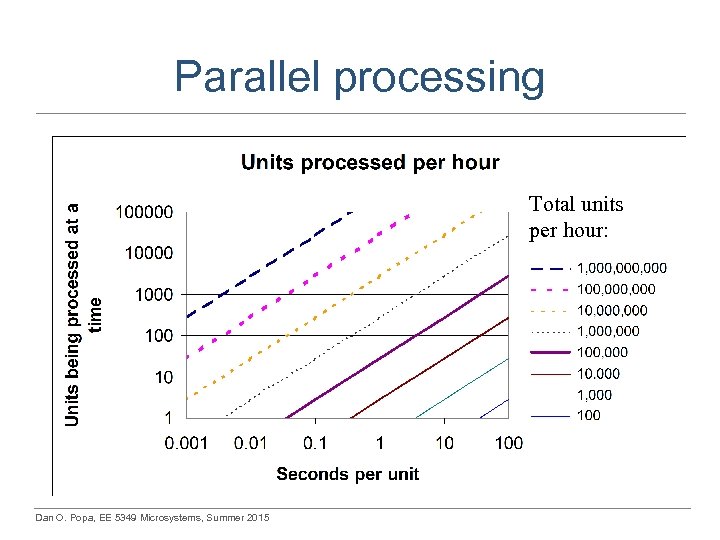Parallel processing Total units per hour: Dan O. Popa, EE 5349 Microsystems, Summer 2015

Top-Down vs. Bottom-Up Manufacturing • Top-down manufacturing: conventional way for people to build things – Micromachining • Wet chemical machining (Photofab, Lithography, photochemical milling, chemical/electrochemical milling, electroplating, electroforming) • Mechanical machining (ultrasonic, diamond, abrasive jet) • Electrothermal machining (EDM, Laser, Plasma, Electron Beam, Dry Etching) – Microassembly • Pick & Place Robotics • Serial micromanipulation • Parallel micromanipulation – Packaging • Die-scale packaging • Wafer-scale packaging • Bottom-up manufacturing: how nature builds things – Fluidic or field-assisted manipulation – Self-assembly – Exponential/self replication – DNA replication Dan O. Popa, EE 5349 Microsystems, Summer 2015

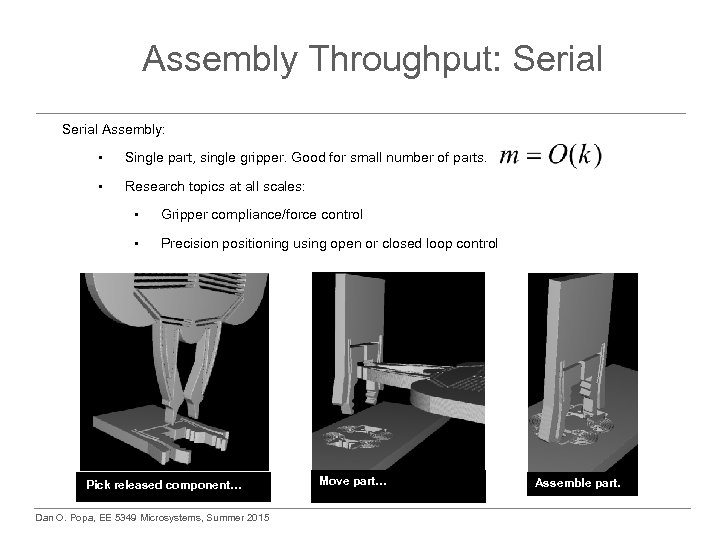Assembly Throughput: Serial Assembly: • Single part, single gripper. Good for small number of parts. • Research topics at all scales: • Gripper compliance/force control • Precision positioning using open or closed loop control Pick released component… Dan O. Popa, EE 5349 Microsystems, Summer 2015 Move part… Assemble part.

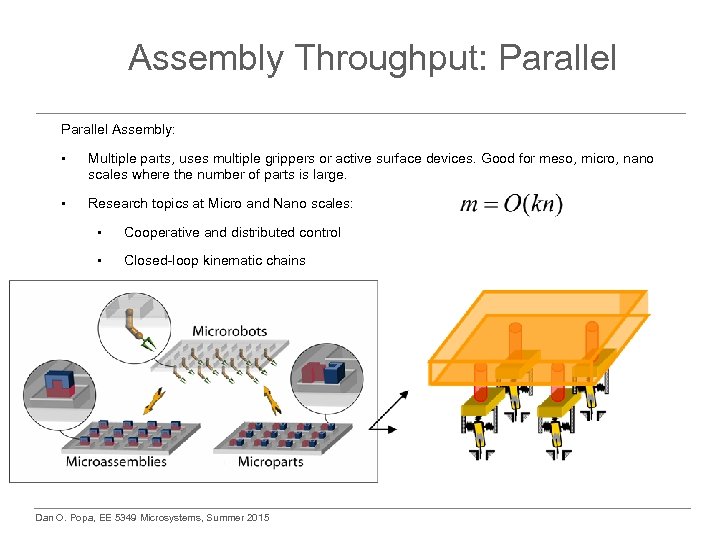Assembly Throughput: Parallel Assembly: • Multiple parts, uses multiple grippers or active surface devices. Good for meso, micro, nano scales where the number of parts is large. • Research topics at Micro and Nano scales: • Cooperative and distributed control • Closed-loop kinematic chains Dan O. Popa, EE 5349 Microsystems, Summer 2015

Assembly Throughput: Exponential Assembly: • Multiple parts, multiple grippers. Good for nano scale where the number of parts is enormous. • Research topics at Micro and Nano scales: • Robot design/fabrication. • Self-replication, control Dan O. Popa, EE 5349 Microsystems, Summer 2015 Assemble an exponentially growing “population” of grippers (m) using k assembly operations.

Top-down manufacturing Dan O. Popa, EE 5349 Microsystems, Summer 2015

Bottom-up and top-down manufacturing Molecular manufacturing video • http: //youtube. com/watch? v=zqy. Z 9 b. Fl_qg Dan O. Popa, EE 5349 Microsystems, Summer 2015

Dan O. Popa, EE 5349 Microsystems, Summer 2015

Scaling Effects • Changes in physics of evolution as parts scale down in size. • Some effects common in nature: quick cooling of Al foil, formation of small droplets of water, electrostatic sticking of hair or small particles, suspension of snow flakes or dust in air. • Volumetric effects (e. g. mass, gravity), replaced by surface effects (e. g. electrostatic attraction, van-der-Waals force). • Describe physics as a function of dimensional scale length (L or D). • Sphere of radius r – surface vs. volume: Dan O. Popa, EE 5349 Microsystems, Summer 2015

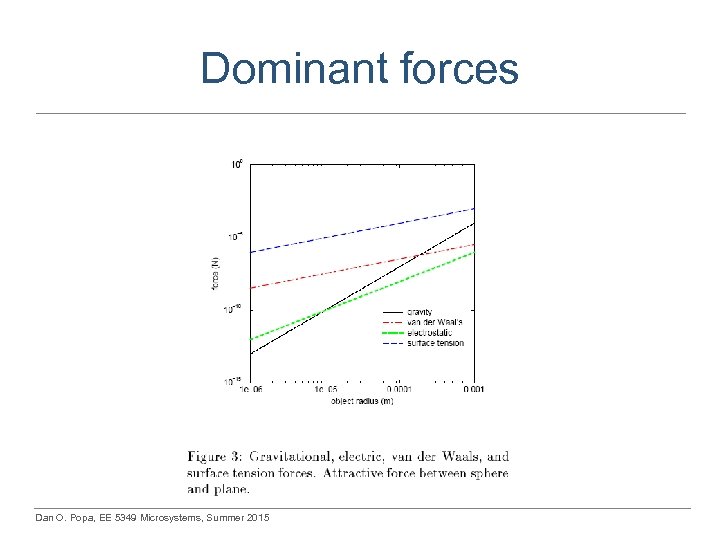Dominant forces Dan O. Popa, EE 5349 Microsystems, Summer 2015

Consequences: Manipulation of small objects • Prehension = Grasping, taking hold of a part Dan O. Popa, EE 5349 Microsystems, Summer 2015

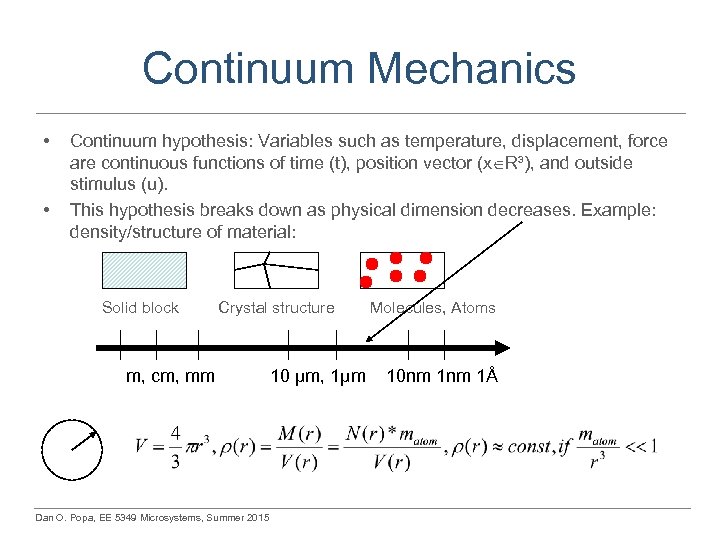Continuum Mechanics • • Continuum hypothesis: Variables such as temperature, displacement, force are continuous functions of time (t), position vector (x R³), and outside stimulus (u). This hypothesis breaks down as physical dimension decreases. Example: density/structure of material: Solid block Crystal structure m, cm, mm Dan O. Popa, EE 5349 Microsystems, Summer 2015 10 µm, 1µm Molecules, Atoms 10 nm 1Å

Continuum Mechanics • • • Conservation laws + constitutive equations. Conservation laws: ex: mass, charge, energy, momentum – integral or differential form. Constitutive equations: intrinsec properties of materials – algebraic relations (ex. Stress and strain are proportional – Hooke’s Law) Combining conservation laws and constitutive equations: laws of continuum mechanics in PDE format. To solve: – use direct integration methods with appropriate boundary conditions. – use discrete approximation in time and space plus numerical methods to find approximate solutions: Finite Element Method Dan O. Popa, EE 5349 Microsystems, Summer 2015

Vector Identities • Relationships between vectors and differential forms. Dot Product, Cross Product “Del” or “Nabla” differential operator F R³ – vector field, f R – scalar function Other vector identities Dan O. Popa, EE 5349 Microsystems, Summer 2015 Gradient Divergence Curl Laplacian Note: Curl of Gradient and Divergence of Curl are always 0.

Integral Identities • These equations help derive differential continuum mechanics laws from integral ones. Stokes Theorem over a Manifold M, ω is a “differential form” Divergence or Gauss Theorem Volume integral of divergence=Flux through the surface Green’s Theorem on a planar contour Stokes theorems of curl for surfaces and volumes Dan O. Popa, EE 5349 Microsystems, Summer 2015

Physics of Evolution for MST • Motion of solids (Newton-Euler laws) – Static Elasticity (Navier’s equations) – Vibratory Motion (Wave equation) • Heat Conduction (Fourier’s law) • Thermal Expansion • Fluid flow (Navier-Stokes equations) • Electromagnetism (Maxwell’s equations) • Piezoelectricity (coupled electromechanical eqns). Dan O. Popa, EE 5349 Microsystems, Summer 2015

Scaling of Flow • Flow regime determined by Reynold’s number: » » - density of fluid (kg/m 3) v- velocity of flow (m/s) r- dimensional scale (m) - viscosity of fluids (cp or kg/m/s) Scaling assumption, T – constant time, - constant => Low length scales, r<<1 => very low Re number (laminar-creeping flow) Particle of radius r in air Viscous drag (F) + Buoyancy (B) At equilibrium Gravity=G Dan O. Popa, EE 5349 Microsystems, Summer 2015 Therefore, T (time to fall) → , if r→ 0 Consequence: small (µm or lower size) dust particles settle to the cleanroom floor in a very long time (hours-days)

Scaling of Elastic Strength • Stiffness of cantilever beams – – – – – E – Young’s Modulus (N/m) L – Beam Length (m) t – Beam thickness and width (m) I – Area Moment of Inertia (m 4) w(x) – beam weight per unit length (kgf/m) u(x) – beam deflection (m) x – distance from fixed point u/ x – slope of beam EI 2 u/ x 2 – bending moment EI 3 u/ x 3 – shear force Euler-Bernoulli equation and boundary conditions for beam with solution Dan O. Popa, EE 5349 Microsystems, Summer 2015

Scaling of Elastic Strength • Scaling of stiffness for cantilever beams: If force is volumetric (gravity) If force is surface (like pressure) Conclusion: if L<<1, kv<

Scaling of Buckling Strength Dan O. Popa, EE 5349 Microsystems, Summer 2015

Scaling of Thermal Effects Dan O. Popa, EE 5349 Microsystems, Summer 2015

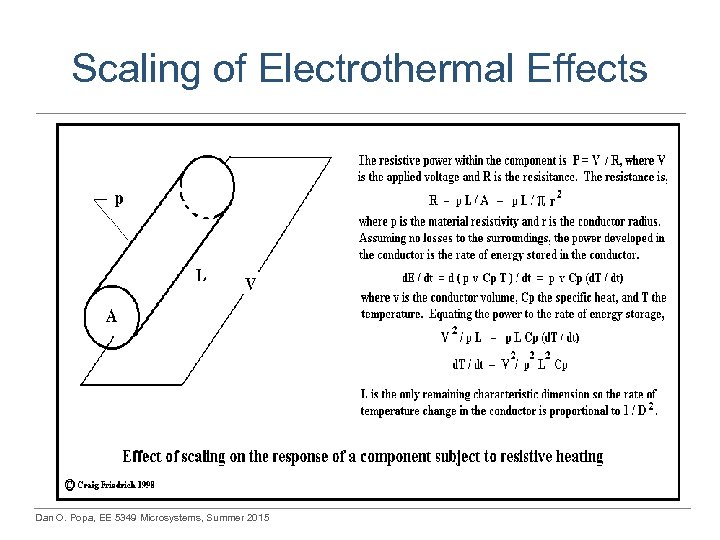Scaling of Electrothermal Effects Dan O. Popa, EE 5349 Microsystems, Summer 2015

Scaling of Electro/Magneto Statics Levitation condition for particle of radius r in air, with charge Q • Conclusion: much easier to levitate a small sphere with surface charge than volume charge Electrostatic force due to electric field E Gravity=G Levitation condition for small conducting wire of length L, radius r= L passing current I Magnetostatic force due to magnetic field B Gravity=G Dan O. Popa, EE 5349 Microsystems, Summer 2015 • Conclusion: much easier to levitate a small wire with surface currents, rather than volume current.

Reading • http: //ieeexplore. ieee. org/iel 5/66/30318/ 01393053. pdf • http: //citeseer. ist. psu. edu/cache/papers/ cs/7198/http: z. Szrobotics. eecs. berke ley. eduz. Sz~ronfz. Szstick. pdf/fearing 95 s urvey. pdf • Chapter 7 from Madou Text Dan O. Popa, EE 5349 Microsystems, Summer 2015