Lecture slides for Automated Planning Theory and Practice

Lecture slides for Automated Planning: Theory and Practice Chapter 2 Representations for Classical Planning Dana S. Nau CMSC 722, AI Planning University of Maryland, Fall 2004 Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 1

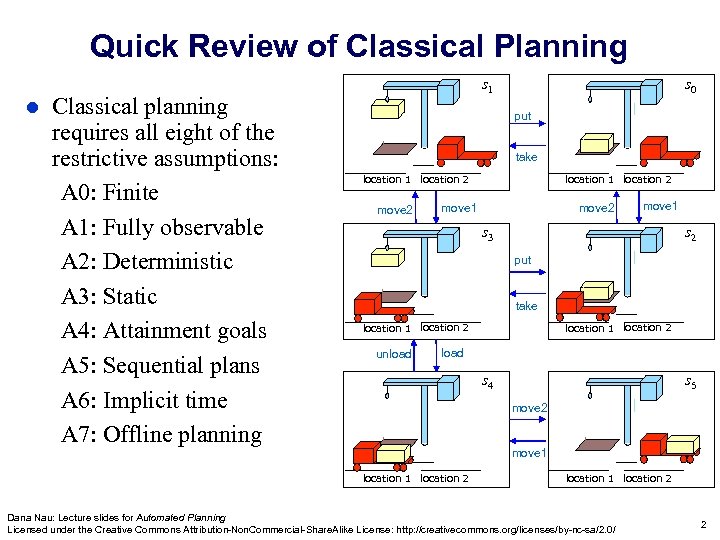Quick Review of Classical Planning l Classical planning requires all eight of the restrictive assumptions: A 0: Finite A 1: Fully observable A 2: Deterministic A 3: Static A 4: Attainment goals A 5: Sequential plans A 6: Implicit time A 7: Offline planning s 1 s 0 put take location 1 location 2 move 1 s 3 s 2 put take location 1 location 2 unload location 1 location 2 load s 4 s 5 move 2 move 1 location 2 location 1 location 2 Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 2

Representations: Motivation In most problems, far too many states to try to represent all of them explicitly as s 0, s 1, s 2, … l Represent each state as a set of features u e. g. , » a vector of values for a set of variables » a set of ground atoms in some first-order language L l Define a set of operators that can be used to compute statetransitions l Don’t give all of the states explicitly u Just give the initial state u Use the operators to generate the other states as needed l Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 3

Outline l Representation schemes u Classical representation u Set-theoretic representation u State-variable representation u Examples: DWR and the Blocks World u Comparisons Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 4

Classical Representation l Start with a function-free first-order language u Finitely many predicate symbols and constant symbols, but no function symbols u Atom: predicate symbol and args - e. g. , on(c 1, c 3), on(c 1, x) u Ground expression: contains no variable symbols - e. g. , on(c 1, c 3) u Unground expression: at least one variable symbol - e. g. , on(c 1, x) u Substitution: = {x 1 v 1, x 2 v 2, …, xn vn} » Each xi is a variable symbol; each vi is a term u Instance of e: result of applying a substitution to e » Replace variables of e simultaneously, not sequentially l State: a set s of ground atoms u The atoms represent the things that are true in one of ’s states u Only finitely many ground atoms, so only finitely many possible states Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 5

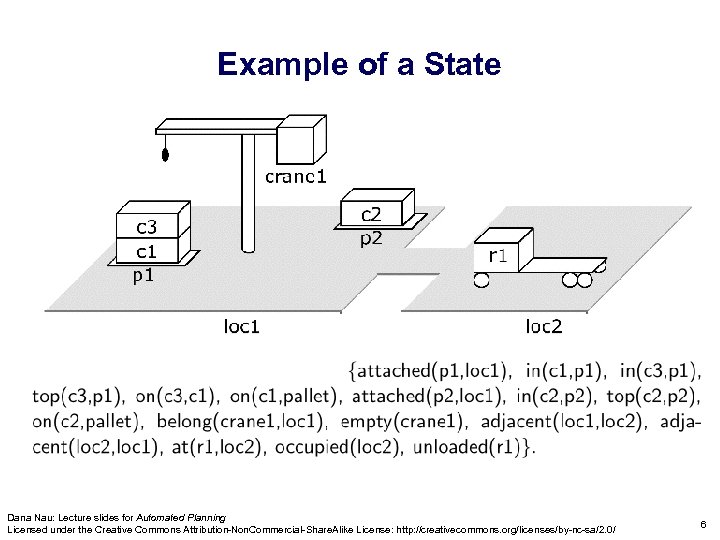Example of a State Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 6

Operators l Operator: a triple o=(name(o), precond(o), effects(o)) u name(o) is a syntactic expression of the form n(x 1, …, xk) » n: operator symbol - must be unique for each operator » x 1, …, xk: variable symbols (parameters) • must include every variable symbol in o u precond(o): preconditions » literals that must be true in order to use the operator u effects(o): effects » literals the operator will make true Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 7

Actions l Action: ground instance (via substitution) of an operator Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 8

Notation Let S be a set of literals. Then u S+ = {atoms that appear positively in S} u S– = {atoms that appear negatively in S} l More specifically, let a be an operator or action. Then u precond+(a) = {atoms that appear positively in a} u precond–(a) = {atoms that appear negatively in a} u effects+(a) = {atoms that appear positively in a} u effects–(a) = {atoms that appear negatively in a} l u effects+(take(k, l, c, d, p) = {holding(k, c), top(d, p)} u effects–(take(k, l, c, d, p) = {empty(k), in(c, p), top(c, p), on(c, d)} Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 9

Applicability l An action a is applicable to a state s if s satisfies precond(a), u i. e. , if precond+(a) s and precond–(a) s = l Here an action and a state that it’s applicable to: Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 10

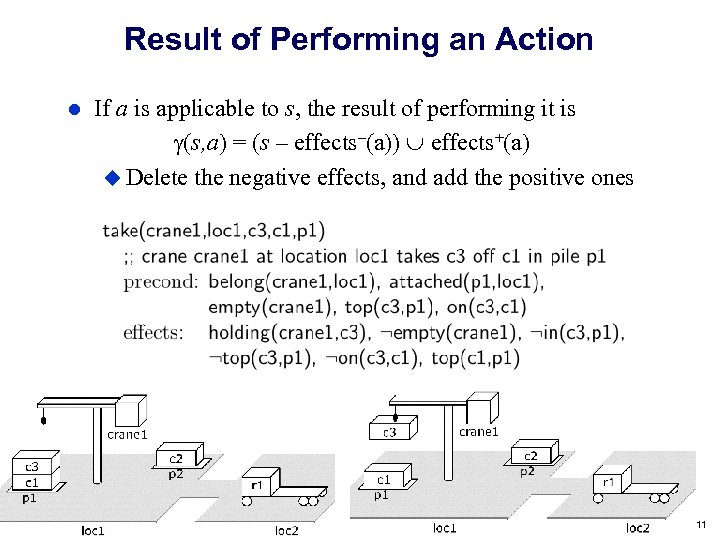Result of Performing an Action l If a is applicable to s, the result of performing it is (s, a) = (s – effects–(a)) effects+(a) u Delete the negative effects, and add the positive ones Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 11

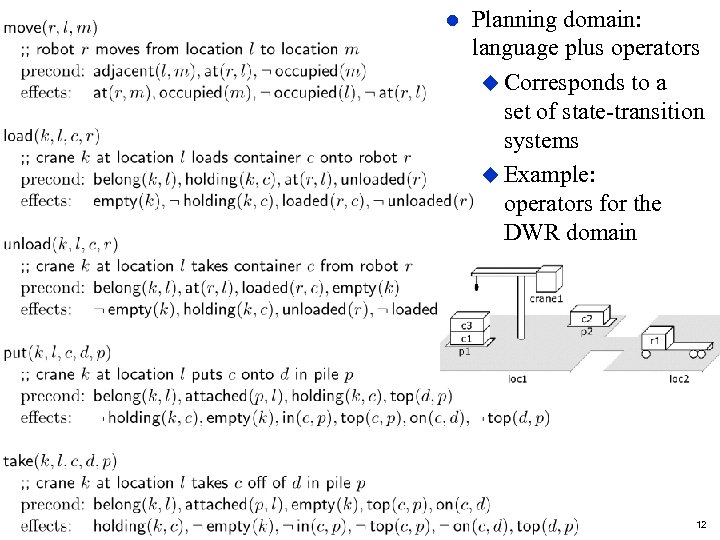l Planning domain: language plus operators u Corresponds to a set of state-transition systems u Example: operators for the DWR domain Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 12

Planning Problems Given a planning domain (language L, operators O) u Statement of a planning problem: a triple P=(O, s 0, g) » O is the collection of operators » s 0 is a state (the initial state) » g is a set of literals (the goal formula) u The actual planning problem: P = ( , s 0, Sg) » s 0 and Sg are as above » = (S, A, ) is a state-transition system » S = {all sets of ground atoms in L} » A = {all ground instances of operators in O} » = the state-transition function determined by the operators l I’ll often say “planning problem” when I mean the statement of the problem l Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 13

Plans and Solutions Plan: any sequence of actions = a 1, a 2, …, an such that each ai is a ground instance of an operator in O l The plan is a solution for P=(O, s 0, g) if it is executable and achieves g u i. e. , if there are states s 0, s 1, …, sn such that » (s 0, a 1) = s 1 » (s 1, a 2) = s 2 » … » (sn– 1, an) = sn » sn satisfies g l Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 14

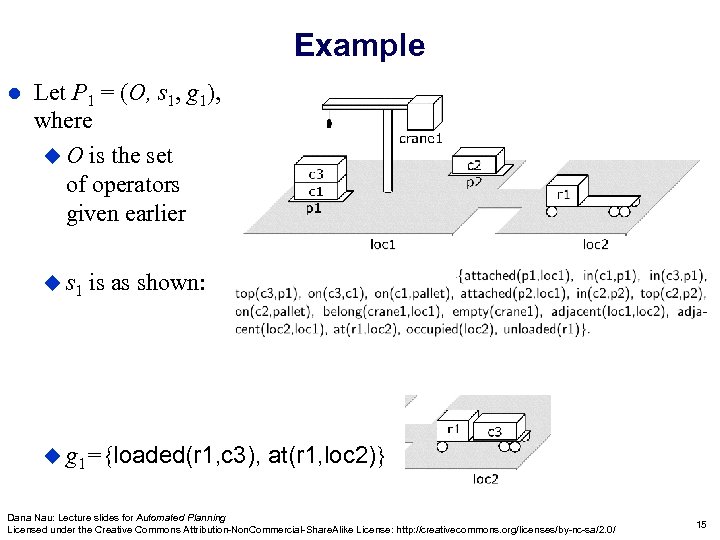Example l Let P 1 = (O, s 1, g 1), where u O is the set of operators given earlier u s 1 is as shown: u g 1={loaded(r 1, c 3), at(r 1, loc 2)} Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 15

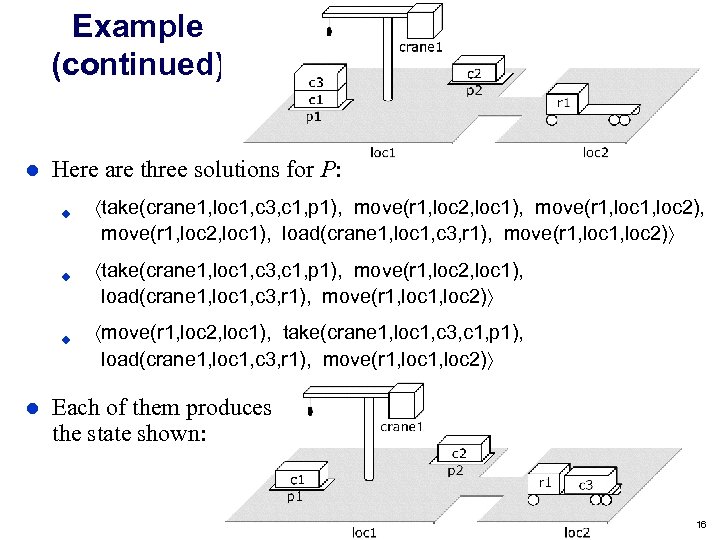Example (continued) l Here are three solutions for P: u u take(crane 1, loc 1, c 3, c 1, p 1), move(r 1, loc 2, loc 1), load(crane 1, loc 1, c 3, r 1), move(r 1, loc 2) u l take(crane 1, loc 1, c 3, c 1, p 1), move(r 1, loc 2, loc 1), move(r 1, loc 2), move(r 1, loc 2, loc 1), load(crane 1, loc 1, c 3, r 1), move(r 1, loc 2) move(r 1, loc 2, loc 1), take(crane 1, loc 1, c 3, c 1, p 1), load(crane 1, loc 1, c 3, r 1), move(r 1, loc 2) Each of them produces the state shown: Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 16

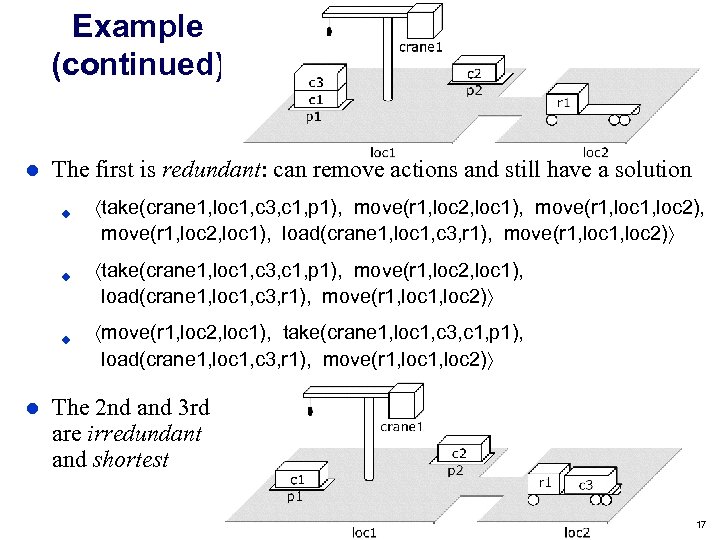Example (continued) l The first is redundant: can remove actions and still have a solution u u take(crane 1, loc 1, c 3, c 1, p 1), move(r 1, loc 2, loc 1), load(crane 1, loc 1, c 3, r 1), move(r 1, loc 2) u l take(crane 1, loc 1, c 3, c 1, p 1), move(r 1, loc 2, loc 1), move(r 1, loc 2), move(r 1, loc 2, loc 1), load(crane 1, loc 1, c 3, r 1), move(r 1, loc 2) move(r 1, loc 2, loc 1), take(crane 1, loc 1, c 3, c 1, p 1), load(crane 1, loc 1, c 3, r 1), move(r 1, loc 2) The 2 nd and 3 rd are irredundant and shortest Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 17

Set-Theoretic Representation l Like classical representation, but restricted to propositional logic l States: u Instead of a collection of ground atoms … {on(c 1, pallet), on(c 1, r 1), on(c 1, c 2), …, at(r 1, l 1), at(r 1, l 2), …} … use a collection of propositions (boolean variables): {on-c 1 -pallet, on-c 1 -r 1, on-c 1 -c 2, …, at-r 1 -l 1, at-r 1 -l 2, …} Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 18

Set-Theoretic Representation l Instead of an operator like this one, … there are lots of actions like this one l take-crane 1 -loc 1 -c 3 -c 1 -p 1 precond: belong-crane 1 -loc 1, attached-p 1 -loc 1, empty-crane 1, top-c 3 -p 1, on-c 3 -c 1 delete: empty-crane 1, in-c 3 -p 1, top-c 3 -p 1, on-c 3 -p 1 add: holding-crane 1 -c 3, top-c 1 -p 1 Exponential blowup u If a classical operator contains n atoms and each atom has arity k, then it corresponds to cnk actions where c = |{constant symbols}| Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 19

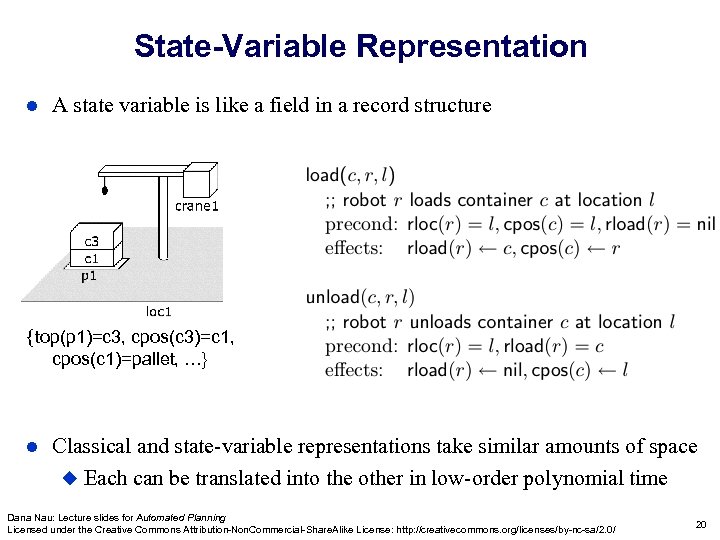State-Variable Representation l A state variable is like a field in a record structure {top(p 1)=c 3, cpos(c 3)=c 1, cpos(c 1)=pallet, …} l Classical and state-variable representations take similar amounts of space u Each can be translated into the other in low-order polynomial time Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 20

Example: The Blocks World Infinitely wide table, finite number of children’s blocks l Ignore where a block is located on the table l A block can sit on the table or on another block l Want to move blocks from one configuration to another u e. g. , l a d initial state c a b e goal b c Can be expressed as a special case of DWR u But the usual formulation is simpler l I’ll give classical, set-theoretic, and state-variable formulations u For the case where there are five blocks l Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 21

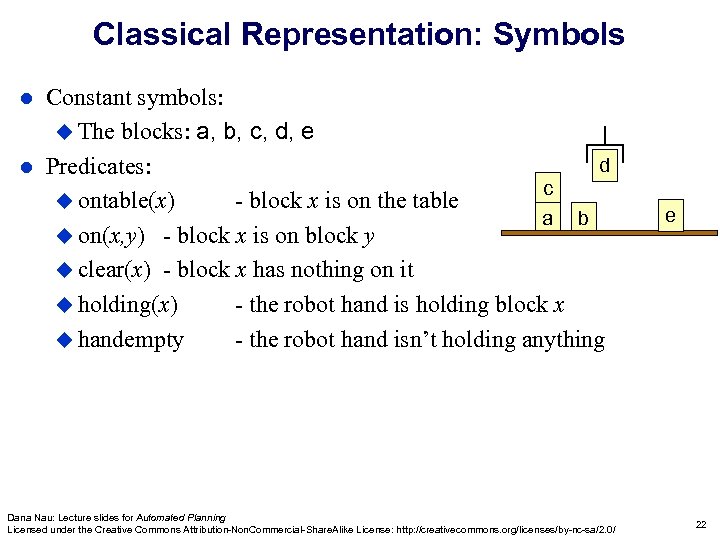Classical Representation: Symbols Constant symbols: u The blocks: a, b, c, d, e d l Predicates: c u ontable(x) - block x is on the table a b u on(x, y) - block x is on block y u clear(x) - block x has nothing on it u holding(x) - the robot hand is holding block x u handempty - the robot hand isn’t holding anything l Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ e 22

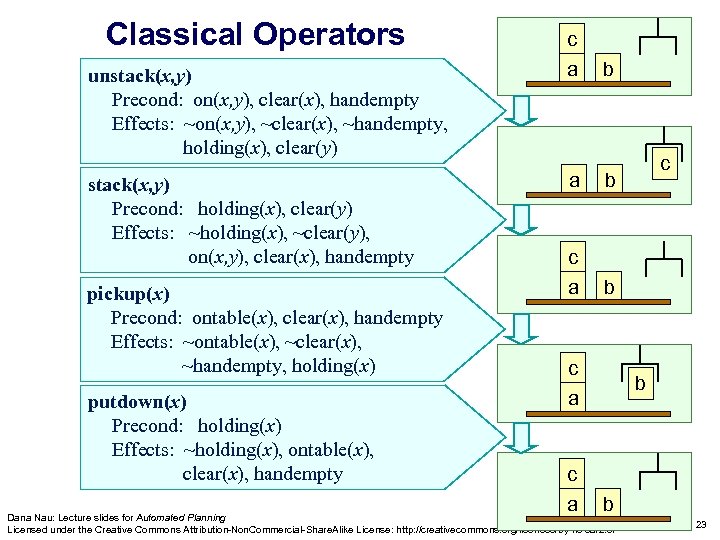Classical Operators unstack(x, y) Precond: on(x, y), clear(x), handempty Effects: ~on(x, y), ~clear(x), ~handempty, holding(x), clear(y) stack(x, y) Precond: holding(x), clear(y) Effects: ~holding(x), ~clear(y), on(x, y), clear(x), handempty pickup(x) Precond: ontable(x), clear(x), handempty Effects: ~ontable(x), ~clear(x), ~handempty, holding(x) putdown(x) Precond: holding(x) Effects: ~holding(x), ontable(x), clear(x), handempty c a b c a c b c a b b Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 23

Set-Theoretic Representation: Symbols For five blocks, there are 36 propositions l Here are 5 of them: d c ontable-a - block a is on the table a b on-c-a - block c is on block a clear-c - block c has nothing on it holding-d - the robot hand is holding block d handempty - the robot hand isn’t holding anything l Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ e 24

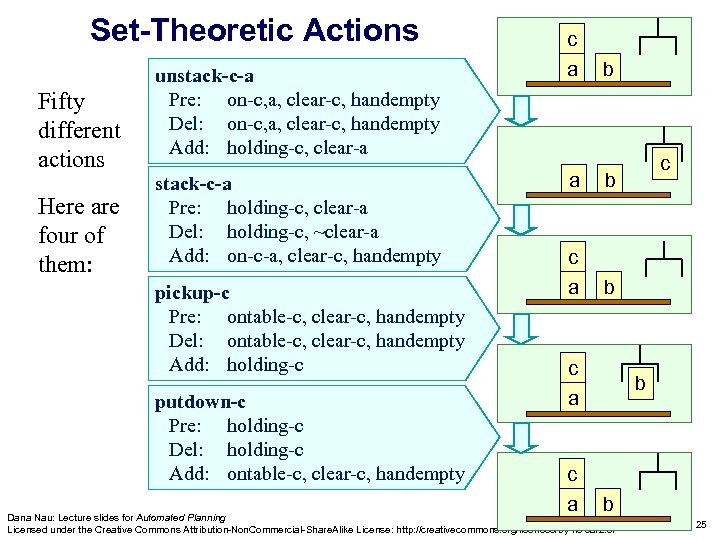Set-Theoretic Actions Fifty different actions Here are four of them: unstack-c-a Pre: on-c, a, clear-c, handempty Del: on-c, a, clear-c, handempty Add: holding-c, clear-a stack-c-a Pre: holding-c, clear-a Del: holding-c, ~clear-a Add: on-c-a, clear-c, handempty pickup-c Pre: ontable-c, clear-c, handempty Del: ontable-c, clear-c, handempty Add: holding-c putdown-c Pre: holding-c Del: holding-c Add: ontable-c, clear-c, handempty c a b c a c b c a b b Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 25

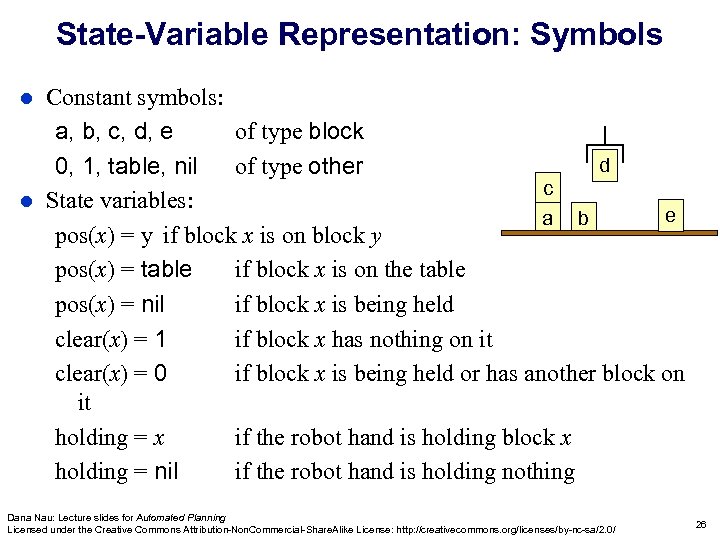State-Variable Representation: Symbols Constant symbols: a, b, c, d, e of type block d 0, 1, table, nil of type other c l State variables: e a b pos(x) = y if block x is on block y pos(x) = table if block x is on the table pos(x) = nil if block x is being held clear(x) = 1 if block x has nothing on it clear(x) = 0 if block x is being held or has another block on it holding = x if the robot hand is holding block x holding = nil if the robot hand is holding nothing l Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 26

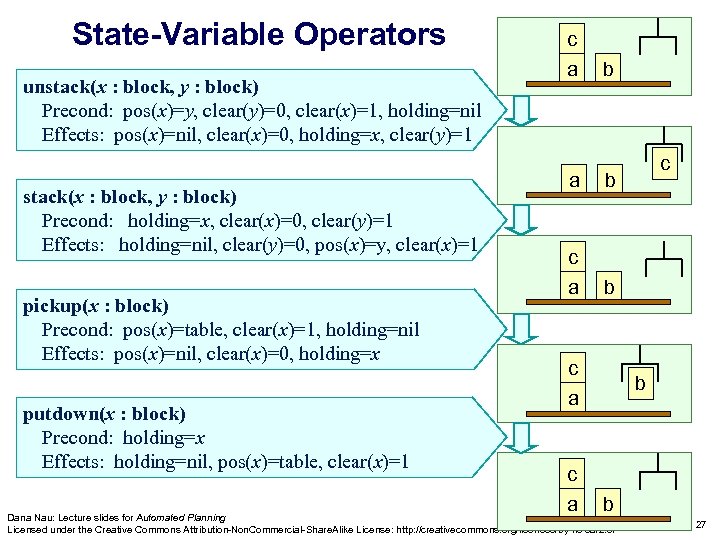State-Variable Operators unstack(x : block, y : block) Precond: pos(x)=y, clear(y)=0, clear(x)=1, holding=nil Effects: pos(x)=nil, clear(x)=0, holding=x, clear(y)=1 stack(x : block, y : block) Precond: holding=x, clear(x)=0, clear(y)=1 Effects: holding=nil, clear(y)=0, pos(x)=y, clear(x)=1 pickup(x : block) Precond: pos(x)=table, clear(x)=1, holding=nil Effects: pos(x)=nil, clear(x)=0, holding=x putdown(x : block) Precond: holding=x Effects: holding=nil, pos(x)=table, clear(x)=1 c a b c a c b c a b b Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 27

Expressive Power Any problem that can be represented in one representation can also be represented in the other two l Can convert in linear time and space, except for the following: u Converting to set-theoretic from either of the others can incur exponential blowup l P(x 1, …, xn) becomes f. P(x 1, …, xn)=1 trivial Set-theoretic representation Classical representation write all of the ground instances State-variable representation f(x 1, …, xn)=y becomes Pf(x 1, …, xn, y) Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 28

Comparison l Classical representation u The most popular for classical planning, partly for historical reasons l Set-theoretic representation u Can take much more space than classical representation u Useful in algorithms that manipulate ground atoms directly » e. g. , planning graphs (Chapter 6), satisfiability (Chapters 7) u Useful for certain kinds of theoretical studies l State-variable representation u Equivalent to classical representation u Less natural for logicians, more natural for engineers u Useful in non-classical planning problems as a way to handle numbers, functions, time Dana Nau: Lecture slides for Automated Planning Licensed under the Creative Commons Attribution-Non. Commercial-Share. Alike License: http: //creativecommons. org/licenses/by-nc-sa/2. 0/ 29