Lecture Outlines Chapter 2 Physics 3 rd Edition

Lecture Outlines Chapter 2 Physics, 3 rd Edition James S. Walker © 2007 Pearson Prentice Hall This work is protected by United States copyright laws and is provided solely for the use of instructors in teaching their courses and assessing student learning. Dissemination or sale of any part of this work (including on the World Wide Web) will destroy the integrity of the work and is not permitted. The work and materials from it should never be made available to students except by instructors using the accompanying text in their classes. All recipients of this work are expected to abide by these restrictions and to honor the intended pedagogical purposes and the needs of other instructors who rely on these materials.

Chapter 2 One-Dimensional Kinematics

Units of Chapter 2 • Position, Distance, and Displacement • Average Speed and Velocity • Instantaneous Velocity • Acceleration • Motion with Constant Acceleration • Applications of the Equations of Motion • Freely Falling Objects

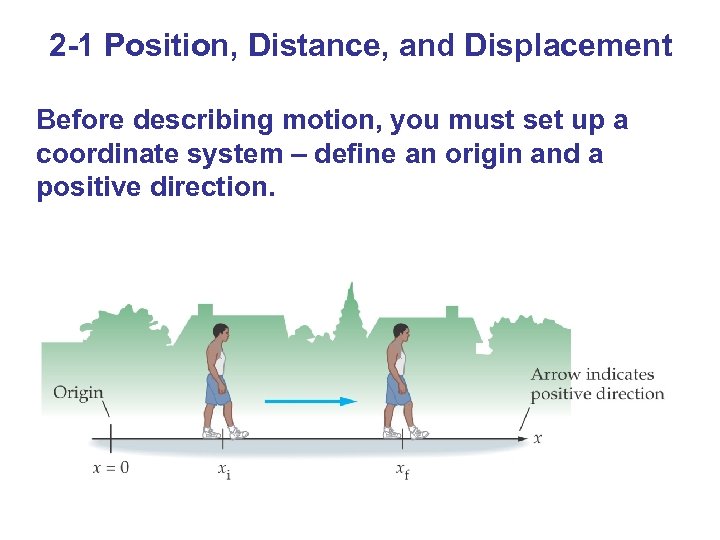2 -1 Position, Distance, and Displacement Before describing motion, you must set up a coordinate system – define an origin and a positive direction.

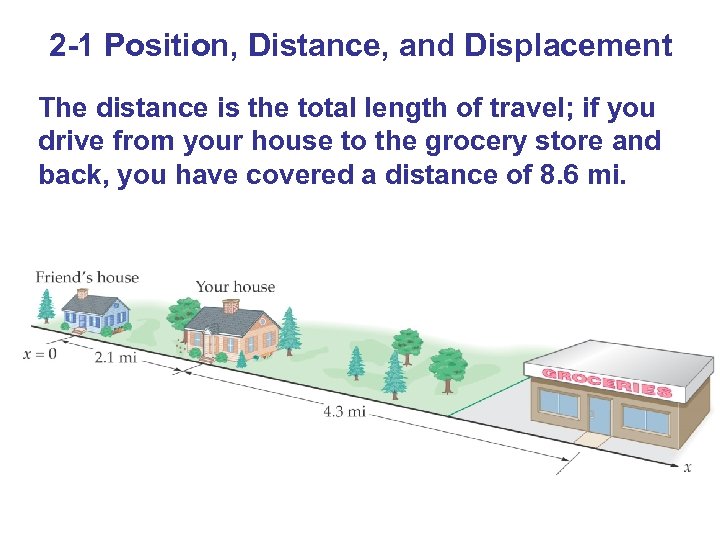2 -1 Position, Distance, and Displacement The distance is the total length of travel; if you drive from your house to the grocery store and back, you have covered a distance of 8. 6 mi.

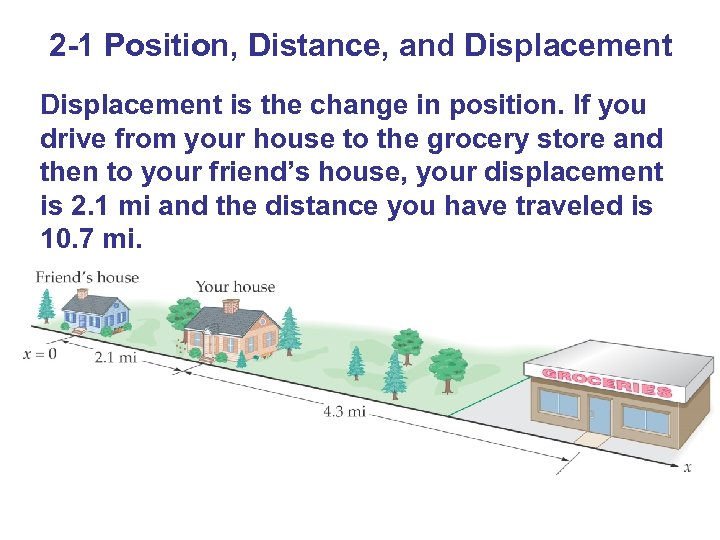2 -1 Position, Distance, and Displacement is the change in position. If you drive from your house to the grocery store and then to your friend’s house, your displacement is 2. 1 mi and the distance you have traveled is 10. 7 mi.

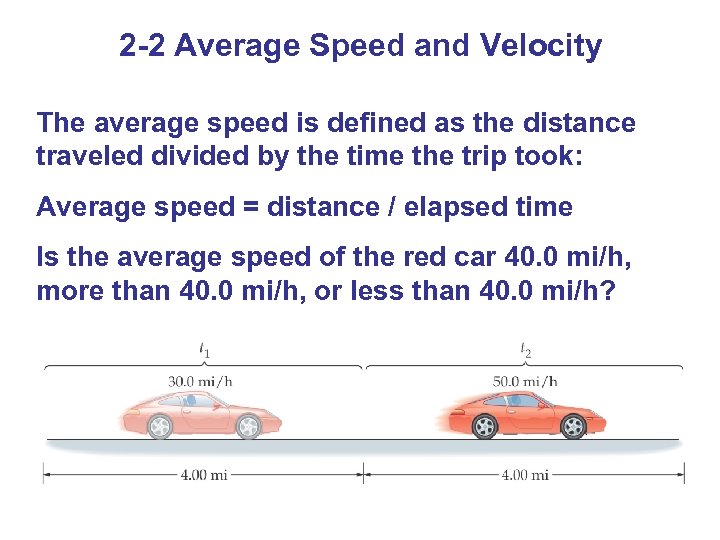2 -2 Average Speed and Velocity The average speed is defined as the distance traveled divided by the time the trip took: Average speed = distance / elapsed time Is the average speed of the red car 40. 0 mi/h, more than 40. 0 mi/h, or less than 40. 0 mi/h?

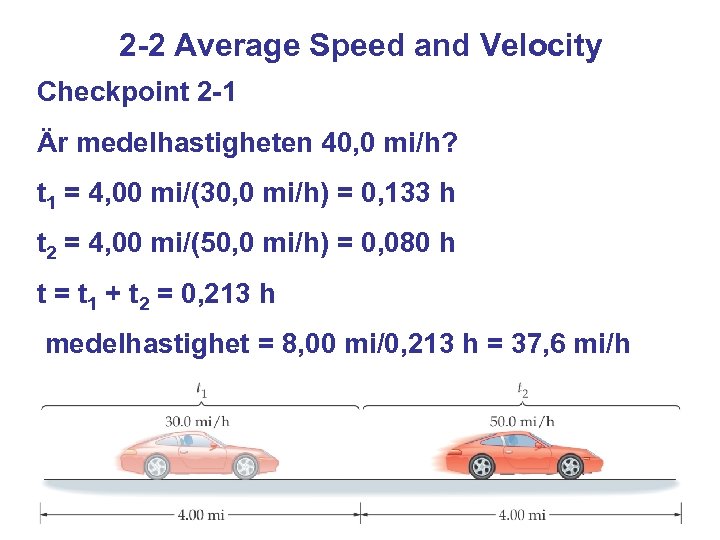2 -2 Average Speed and Velocity Checkpoint 2 -1 Är medelhastigheten 40, 0 mi/h? t 1 = 4, 00 mi/(30, 0 mi/h) = 0, 133 h t 2 = 4, 00 mi/(50, 0 mi/h) = 0, 080 h t = t 1 + t 2 = 0, 213 h medelhastighet = 8, 00 mi/0, 213 h = 37, 6 mi/h

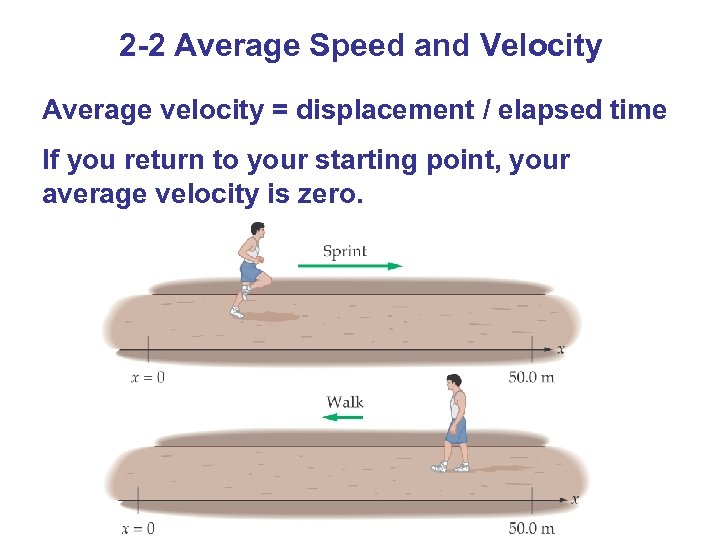2 -2 Average Speed and Velocity Average velocity = displacement / elapsed time If you return to your starting point, your average velocity is zero.

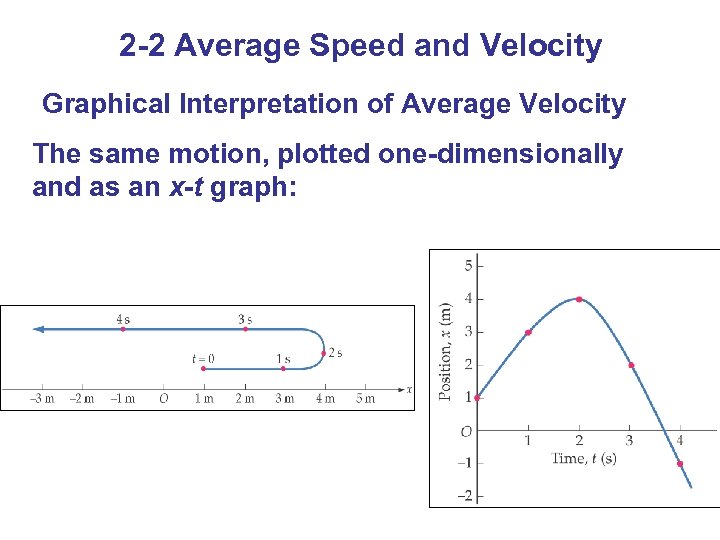2 -2 Average Speed and Velocity Graphical Interpretation of Average Velocity The same motion, plotted one-dimensionally and as an x-t graph:

2 -3 Instantaneous Velocity Definition: (2 -4) This means that we evaluate the average velocity over a shorter and shorter period of time; as that time becomes infinitesimally small, we have the instantaneous velocity.

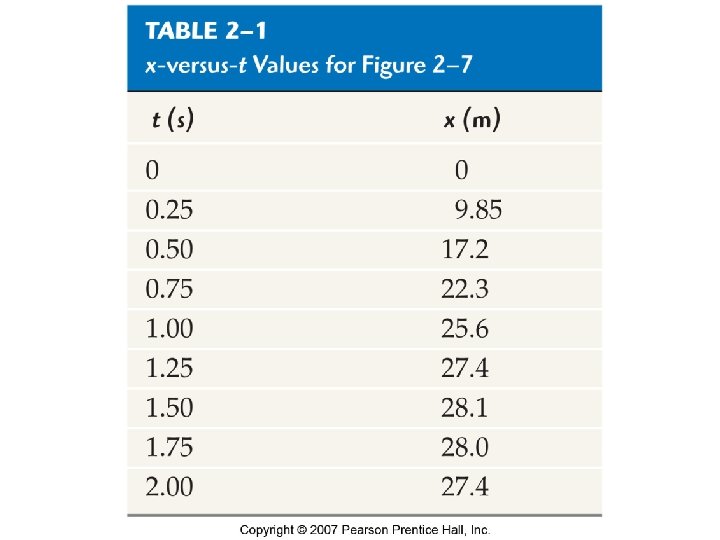Table 2 -1 x-versus-t Values for Figure 2 -7

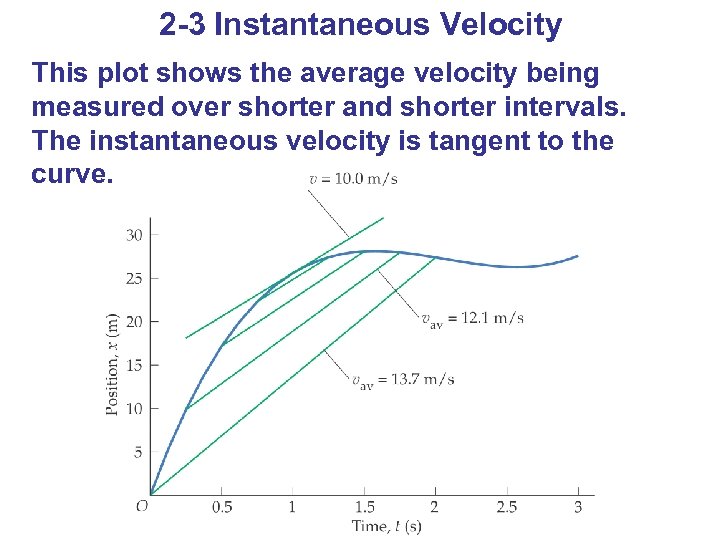2 -3 Instantaneous Velocity This plot shows the average velocity being measured over shorter and shorter intervals. The instantaneous velocity is tangent to the curve.

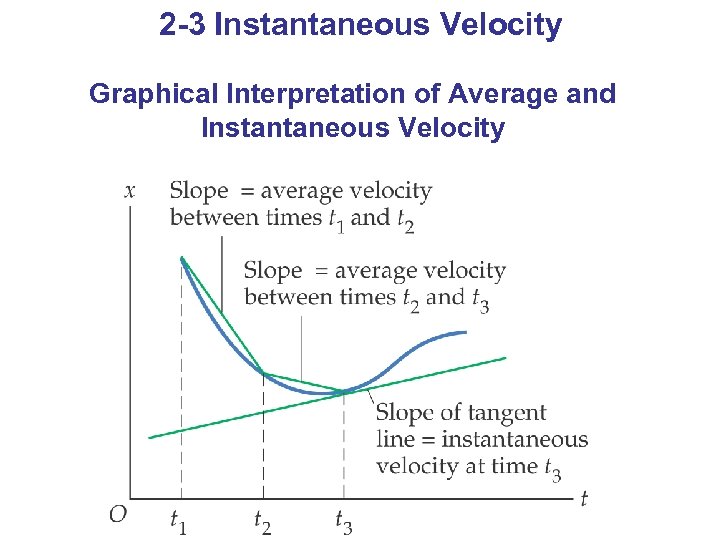2 -3 Instantaneous Velocity Graphical Interpretation of Average and Instantaneous Velocity

2 -4 Acceleration Average acceleration: (2 -5)

2 -4 Acceleration Exercise 2 -1 Acceleration från stillastående till 60 mi/h (26, 8 m/s) på 6, 2 s Ger med nedanstående formel aav = (26, 8 m/s – 0 m/s) /6, 2 s = 4, 3 m/s 2

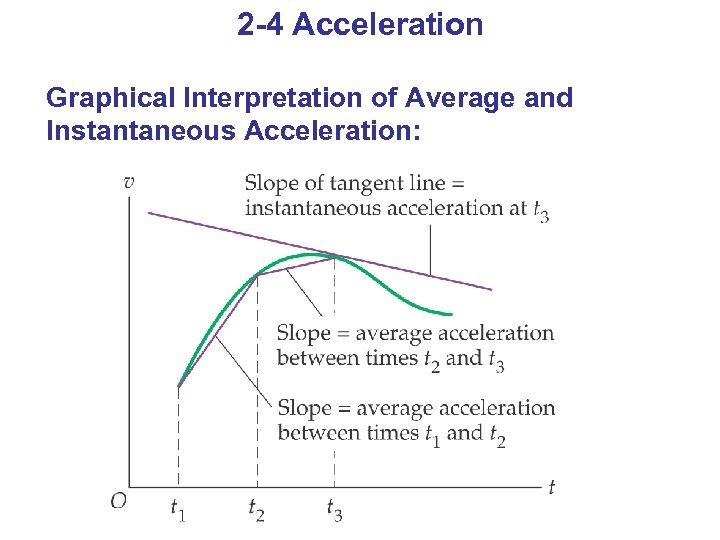2 -4 Acceleration Graphical Interpretation of Average and Instantaneous Acceleration:

2 -4 Acceleration Om accelerationen är konstant är Average Acceleration identisk med Instantaneous Acceleration

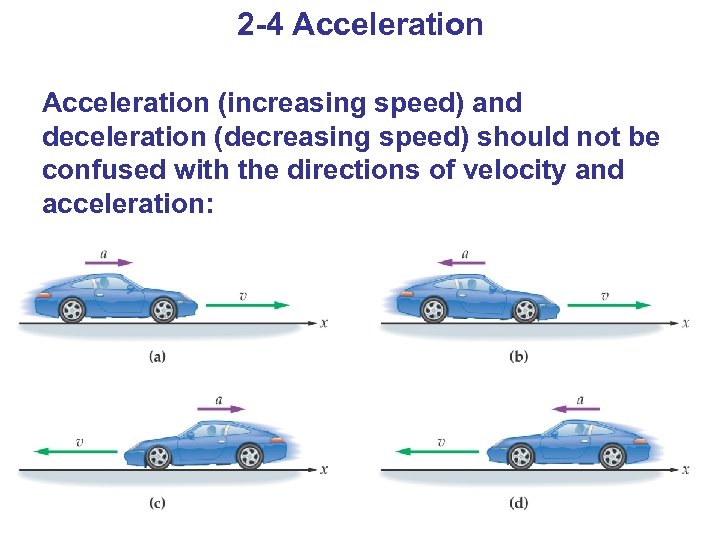2 -4 Acceleration (increasing speed) and deceleration (decreasing speed) should not be confused with the directions of velocity and acceleration:

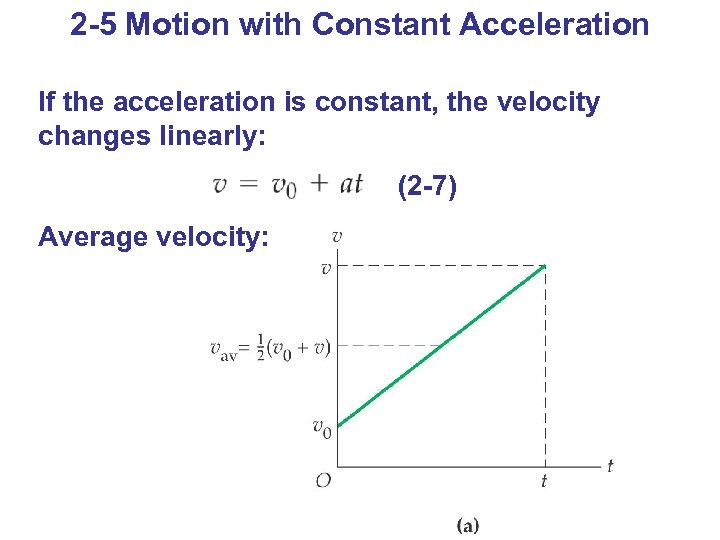2 -5 Motion with Constant Acceleration If the acceleration is constant, the velocity changes linearly: (2 -7) Average velocity:

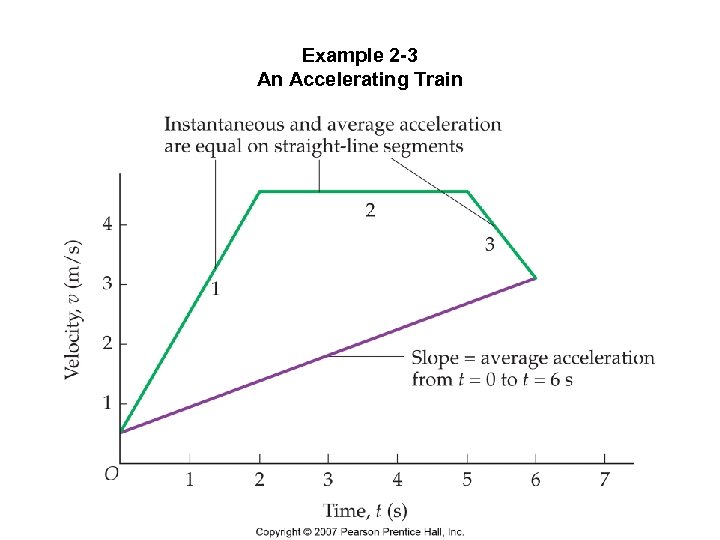Example 2 -3 An Accelerating Train

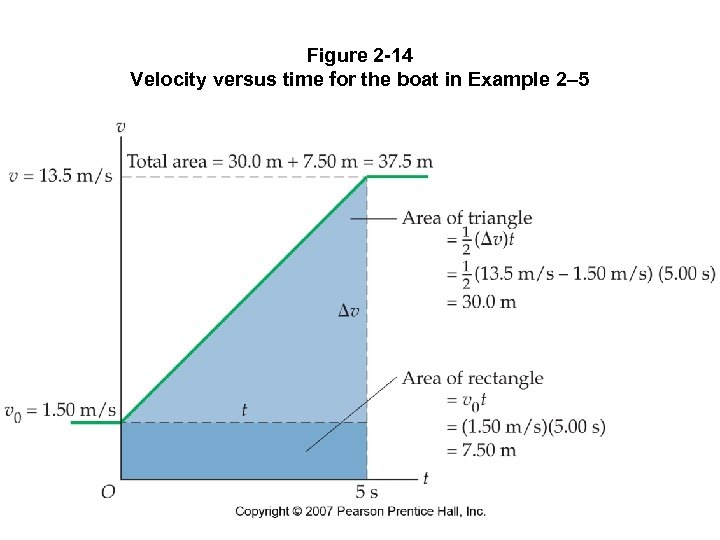Figure 2 -14 Velocity versus time for the boat in Example 2– 5

2 -5 Motion with Constant Acceleration Average velocity: (2 -9) Position as a function of time: (2 -10) (2 -11) Velocity as a function of position: (2 -12)

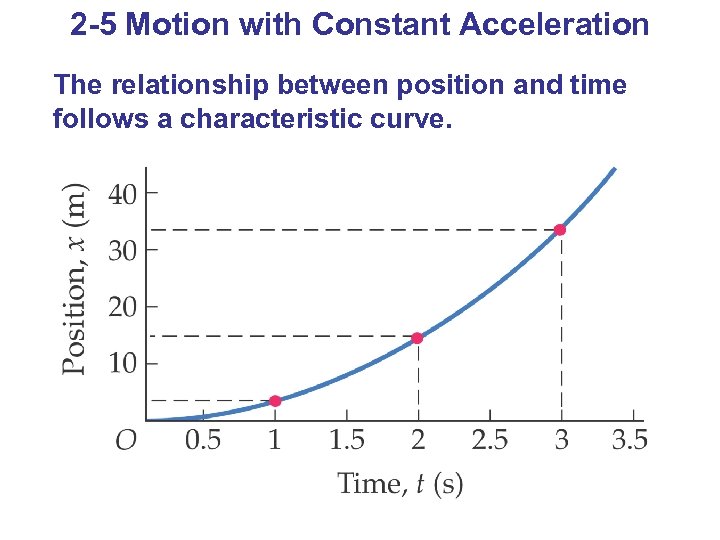2 -5 Motion with Constant Acceleration The relationship between position and time follows a characteristic curve.

2 -5 Motion with Constant Acceleration Sista ekvationen mellan v och x (då accelerationen är konstant) fås med hjälp av (2 -7) ger att t = (v-v 0)/a som insatt i (2 -10) vav = (x –x 0)/(t-0) men vav = (v 0 + v)/2 (2 -9) vilket slutligen ger (2 -12) x = x 0 + vav t = x 0 + (v-v 0)(v+v 0)/2 a x = x 0 + (v 2 – v 02)/2 a

2 -5 Motion with Constant Acceleration

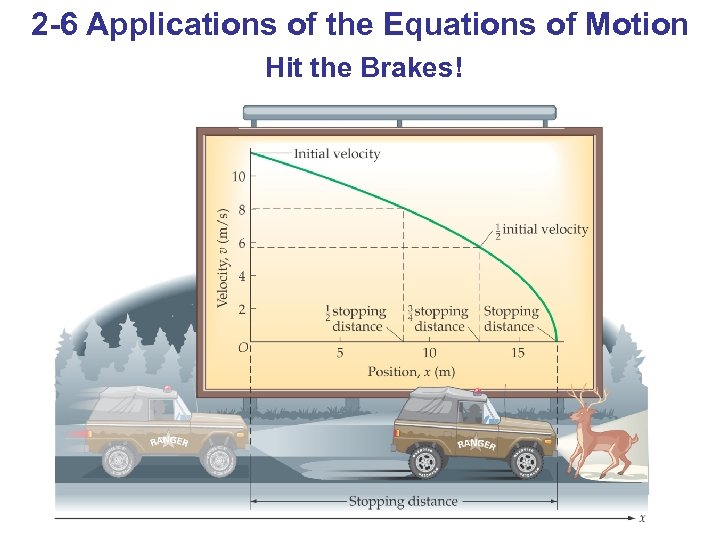2 -6 Applications of the Equations of Motion Hit the Brakes!

2 -7 Freely Falling Objects Free fall is the motion of an object subject only to the influence of gravity. The acceleration due to gravity is a constant, g.

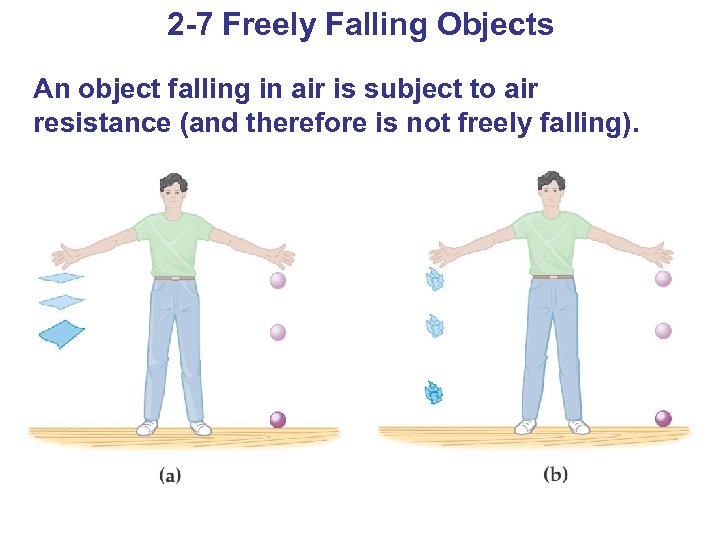2 -7 Freely Falling Objects An object falling in air is subject to air resistance (and therefore is not freely falling).

2 -7 Freely Falling Objects Free fall from rest:

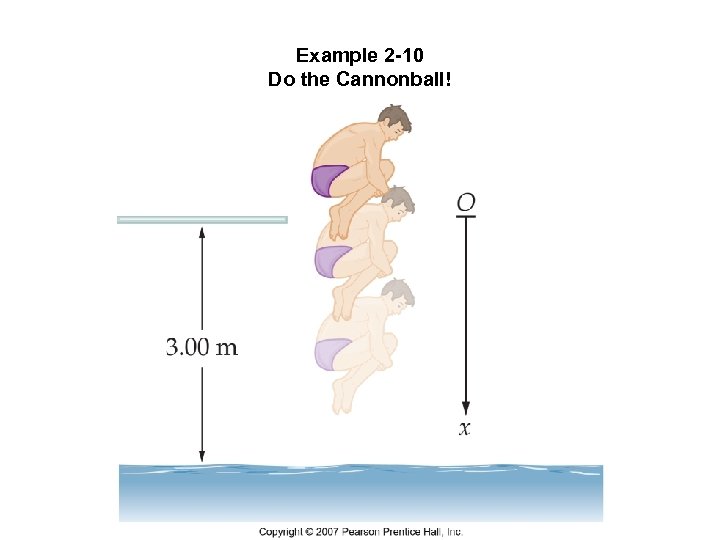Example 2 -10 Do the Cannonball!

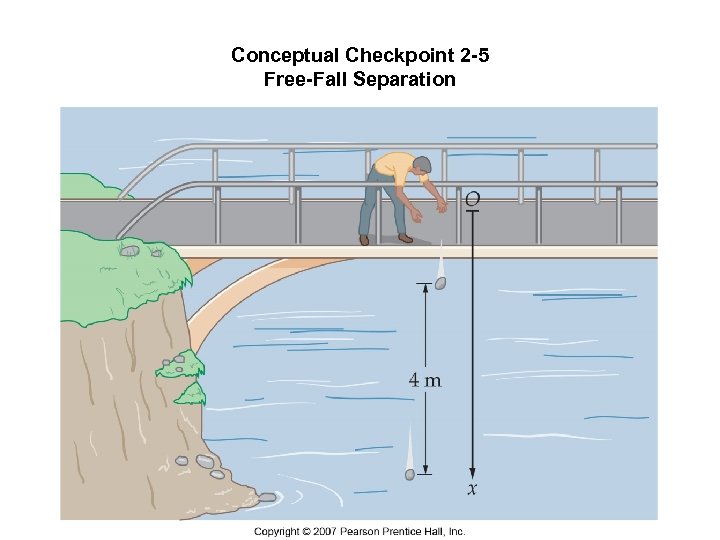Conceptual Checkpoint 2 -5 Free-Fall Separation

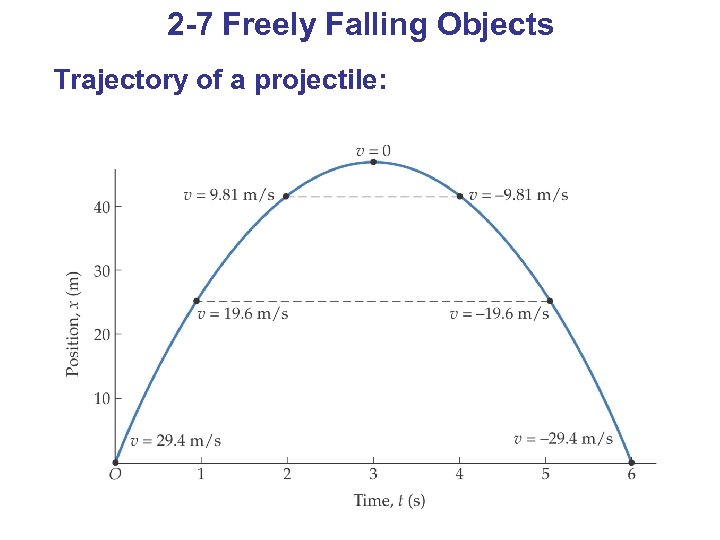2 -7 Freely Falling Objects Trajectory of a projectile:

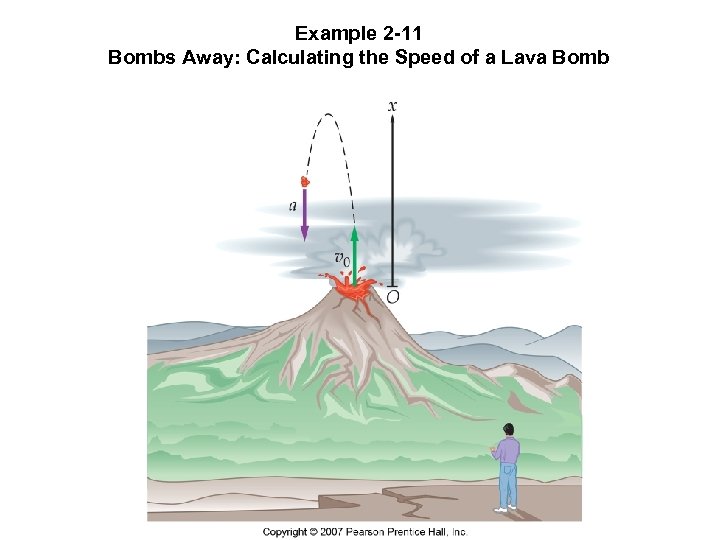Example 2 -11 Bombs Away: Calculating the Speed of a Lava Bomb

Summary of Chapter 2 • Distance: total length of travel • Displacement: change in position • Average speed: distance / time • Average velocity: displacement / time • Instantaneous velocity: average velocity measured over an infinitesimally small time

Summary of Chapter 2 • Instantaneous acceleration: average acceleration measured over an infinitesimally small time • Average acceleration: change in velocity divided by change in time • Deceleration: velocity and acceleration have opposite signs • Constant acceleration: equations of motion relate position, velocity, acceleration, and time • Freely falling objects: constant acceleration g = 9. 81 m/s 2