Lecture 7 Machining Tool Life Wear and Failure

Lecture 7: Machining Tool Life: Wear and Failure Faculty of Mechanical Engineering- Technion Israel Institute of Technology ©

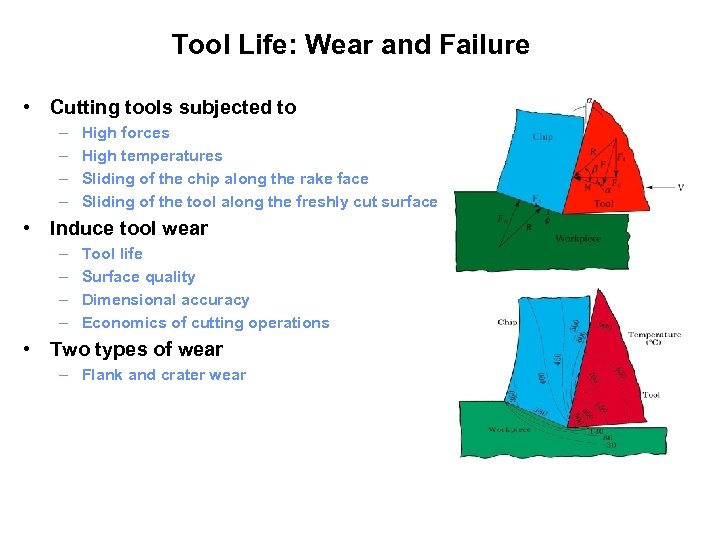Tool Life: Wear and Failure • Cutting tools subjected to – – High forces High temperatures Sliding of the chip along the rake face Sliding of the tool along the freshly cut surface • Induce tool wear – – Tool life Surface quality Dimensional accuracy Economics of cutting operations • Two types of wear – Flank and crater wear

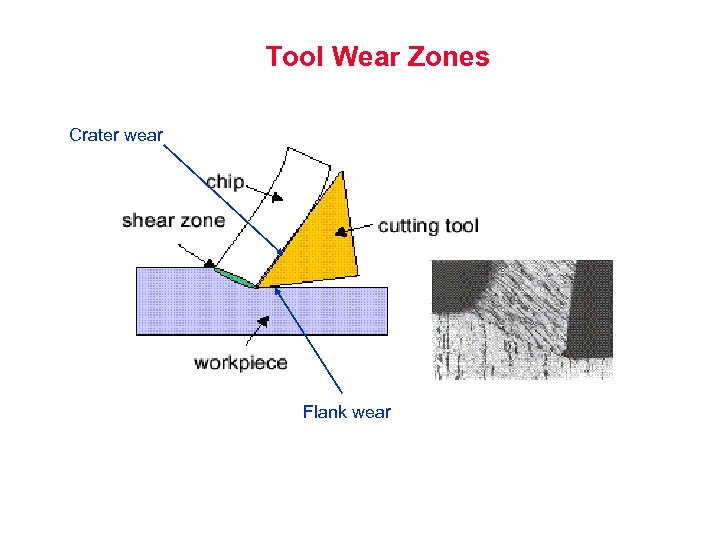Tool Wear Zones Crater wear Flank wear

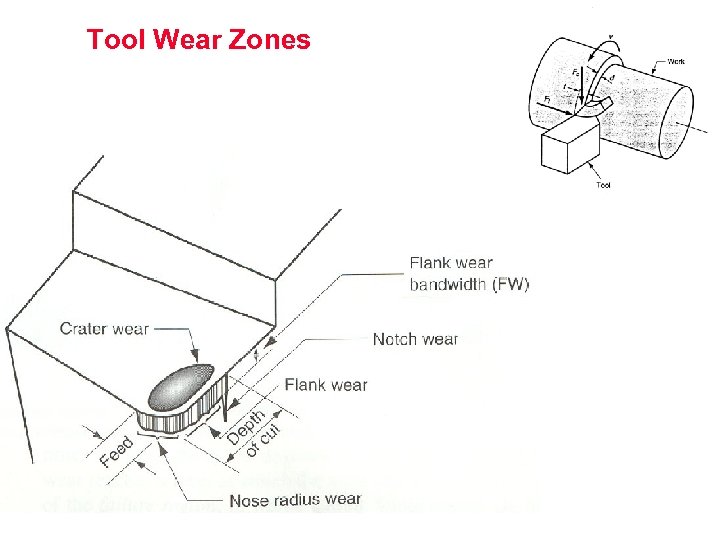Tool Wear Zones

Tool Wear

Tool / Chip Interface

Tool Wear Zones • Crater wear (crater, )מכתש – tool-chip interface – predominant at high speeds – mitigated by efficient use of carbides • Flank wear (wear land, )פאת שחרור – tool-workpiece interface – predominant at low speeds

Failure/Wear Mechanisms 1) Premature Fracture: • Fatigue 2) Wear development • Abrasive wear • Chemical diffusion wear • Adhesive wear

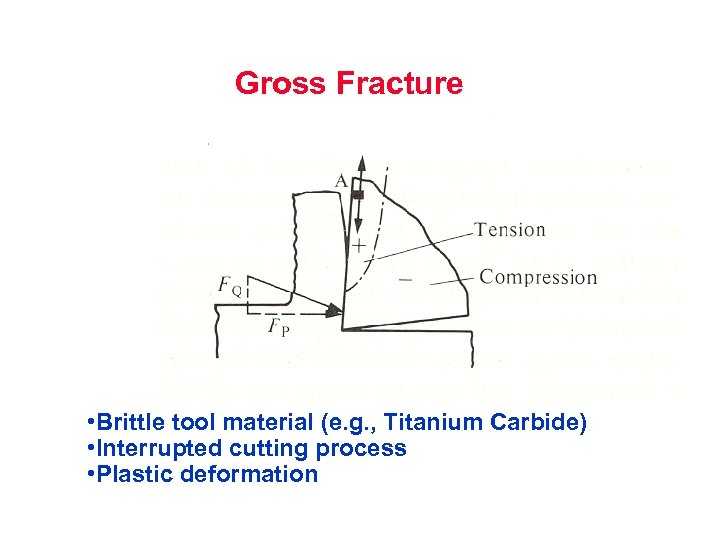Gross Fracture • Brittle tool material (e. g. , Titanium Carbide) • Interrupted cutting process • Plastic deformation

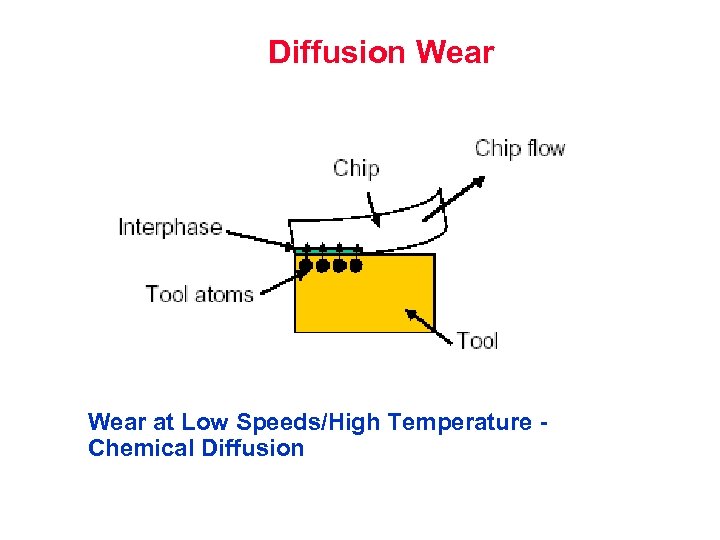Diffusion Wear at Low Speeds/High Temperature Chemical Diffusion

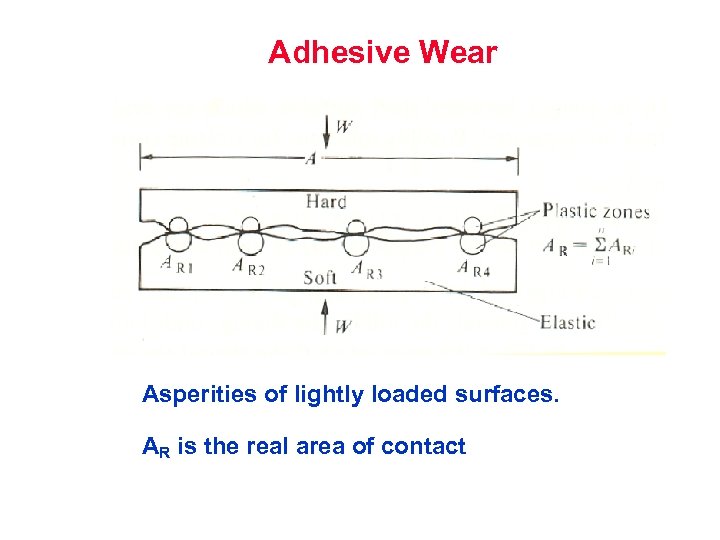Adhesive Wear Asperities of lightly loaded surfaces. AR is the real area of contact

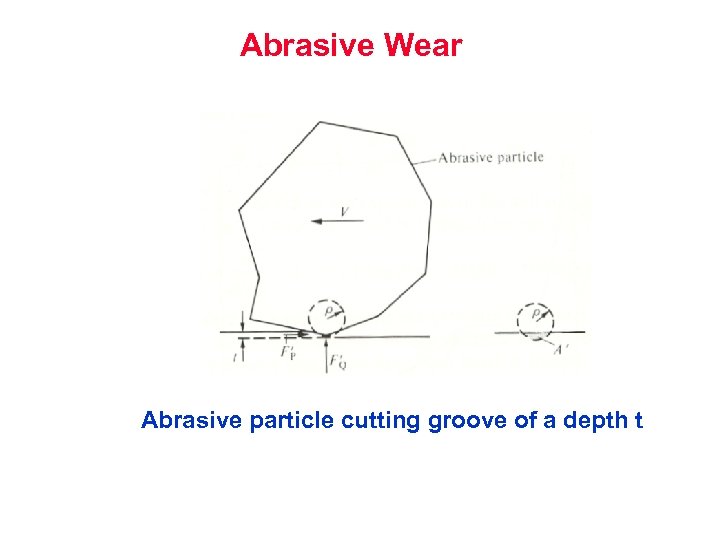Abrasive Wear Abrasive particle cutting groove of a depth t

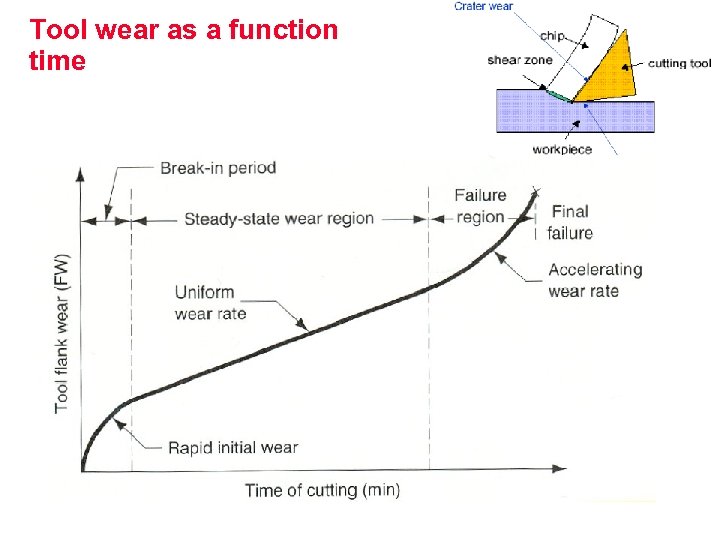Tool wear as a function time

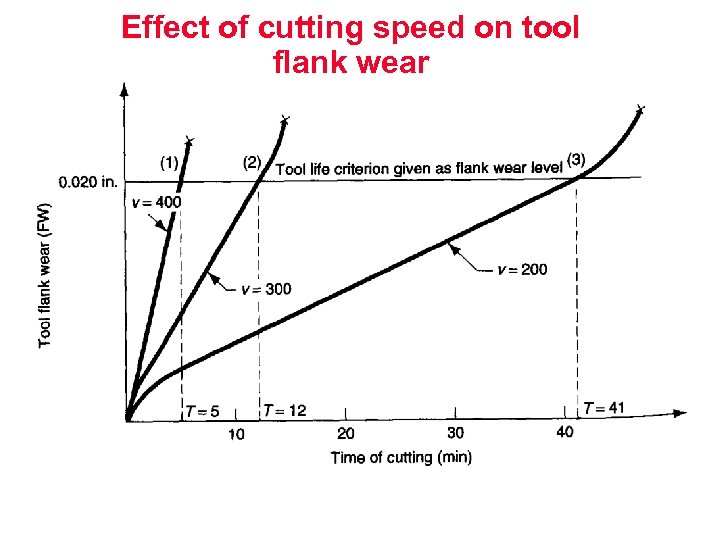Effect of cutting speed on tool flank wear

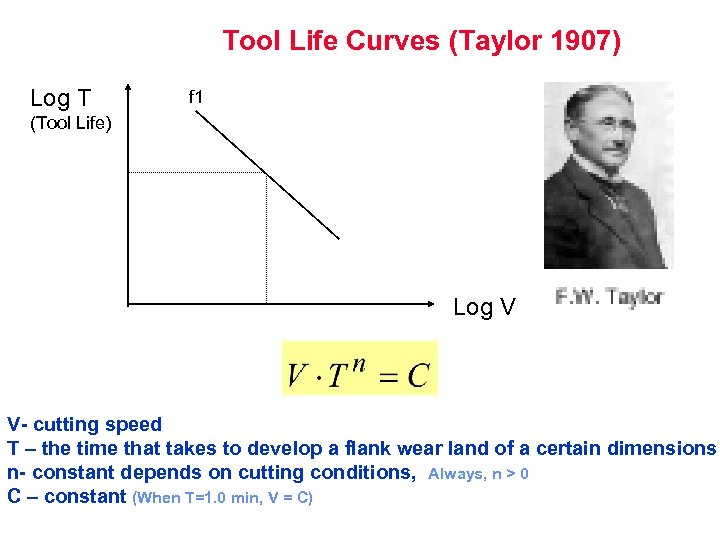Tool Life Curves (Taylor 1907) Log T f 1 (Tool Life) Log V V- cutting speed T – the time that takes to develop a flank wear land of a certain dimensions n- constant depends on cutting conditions, Always, n > 0 C – constant (When T=1. 0 min, V = C)

Taylor’s Equation for Tool Life • VTn = C • Tool-life curve –Log-log curve –T = (C/V)1/n C –Log. T = 1/n log. C – 1/n log. V Tool-life curves for a variety of cutting-tool materials. The negative inverse of the slope of these curves is the exponent n in the Taylor tool-life equations and C is the cutting speed at T = 1 min.

Taylor’s Equation for Tool Life • VTn = C – Given (V 1, T 1) & (V 2, T 2) from testing – What are n and C? • V 1 T 1 n = C, – – V 2 T 2 n = C V 1 T 1 n = V 2 T 2 n (T 1 / T 2 )n = V 2 / V 1 Then n = log (V 2 / V 1) / log (T 1 / T 2) Or n =[ log (V 2) – log (V 1)] / [log (T 1)- log (T 2)] • Once we get n, then C = V 1 T 1 n

n =[ log (V 2) – log (V 1)] / [log (T 1)- log (T 2)] T 2 T 1 C V 2 V 1

[log (T 1)- log (T 2)] n =[ log (V 2) – log (V 1)] / [log (T 1)- log (T 2)] [log (V 2) – log (V 1)] C