Lecture 6 KEYNESIAN ECONOMICS FISCAL POLICY

Lecture 6 KEYNESIAN ECONOMICS & FISCAL POLICY

AGGREGATE OUTPUT AND INCOME - 1 • Each period (weeks, months, years, etc), firms produce some aggregate quantity of goods and services. • We call this aggregate output (Y). • We have seen that GDP (Y) can be calculated in terms of either income or expenditures.

AGGREGATE OUTPUT AND INCOME - 2 • We will use the variable Y to refer to both aggregate output and aggregate income, because they are the same seen from different points of view.

AGGREGATE OUTPUT AND INCOME - 3 • What happens when output increases? • What happens when output is cut? • In any given period there is an exact quality between aggregate output (production) and aggregate income.

AGGREGATE OUTPUT AND INCOME - 4 • Aggregate output can also be looked on as the aggregate quantity supplied, because that is the amount firms are supplying (producing) during the period.

AGGREGATE OUTPUT AND INCOME - 5 • In the lectures which follow, we use the phrase aggregate output (income), rather than aggregate quantity supplied, but keep in mind that the two are equivalent.

INCOME, CONSUMPTION AND SAVING - 1 • In the analysis which follows, we are initially going to assume a simple world with no government and a ‘closed’ economy - i. e. no imports and no exports. • With their income, households can either consume or save.

INCOME, CONSUMPTION AND SAVING - 2 • Total household saving in the economy (S) is by definition equal to income (Y) minus consumption (C): Saving S Income – Consumption Y–C

INCOME, CONSUMPTION AND SAVING - 3 • The triple equal sign means this is an identity - something that is always true. • In our simple economy, in which there is no government, there are two types of spending behavior - spending by households or consumption (C) and spending by firms, or investment (I)

THE 450 LINE • Divides the angle between the two axes of a graph in half • Has the important property that from any point on it, the vertical and horizontal distances measured along the axes are equal

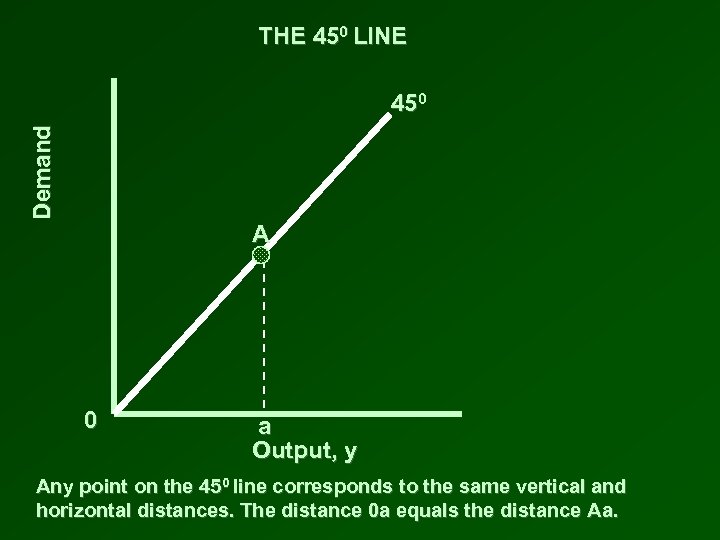THE 450 LINE Demand 450 A 0 a Output, y Any point on the 450 line corresponds to the same vertical and horizontal distances. The distance 0 a equals the distance Aa.

THE SIMPLEST KEYNESIAN CROSS • Uses the 450 line • A graph with the demand for goods and services on the vertical axis and output ( y ) on the horizontal axis • The government and foreign sector are omitted from this model • Only consumers and firms can demand output • Consumers demand consumption goods and firms demand investment goods • Assume initially that consumers and firms demand a fixed amount of goods

CONSUMPTION AND INVESTMENT DEMAND • • • Consumption demand is “C” Investment demand is “I” Total demand is “C + I” In the short run, demand determines output Output = demand = C + I

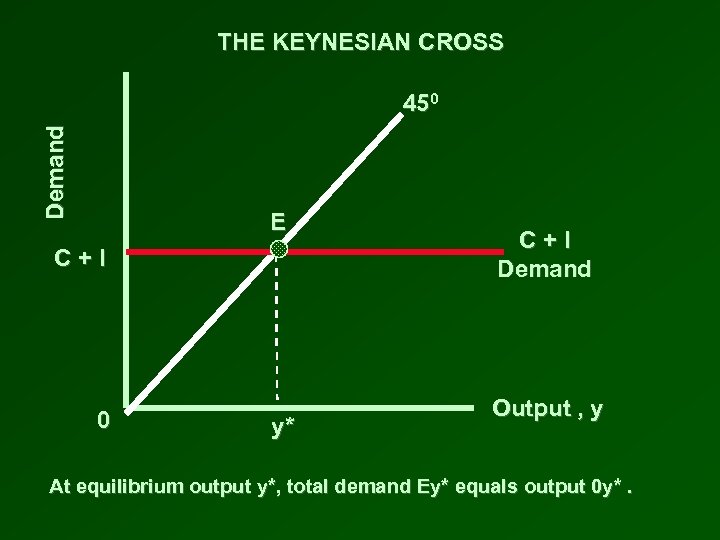THE KEYNESIAN CROSS Demand 450 E C+I 0 y* C+I Demand Output , y At equilibrium output y*, total demand Ey* equals output 0 y*.

THE SIMPLE KEYNESIAN CROSS • Superimpose the horizontal line – C + I (demand) – on the 450 diagram • Total demand is fixed at C + I and is independent of the level of GDP • Equilibrium output is at y*, the level of output at which the demand line crosses the 450 line at point E • Output measured on the horizontal axis equals demand by consumers and firms • Since E is on the 450 line, the vertical distance Ey* equals the horizontal distance 0 y*

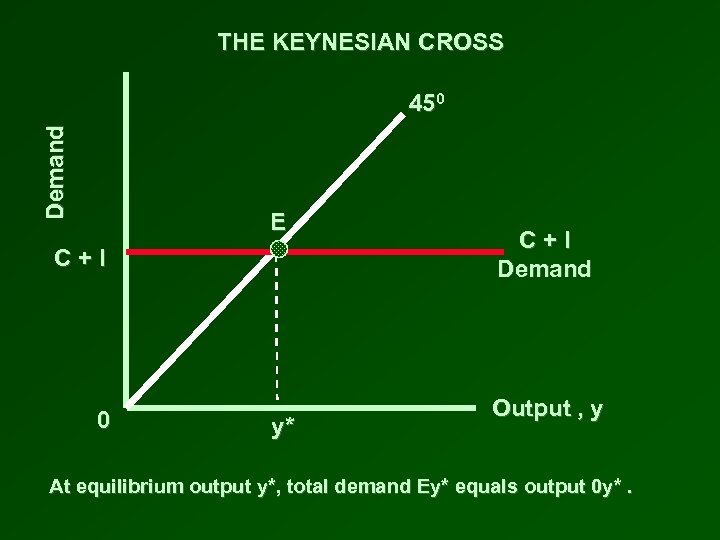THE KEYNESIAN CROSS Demand 450 E C+I 0 y* C+I Demand Output , y At equilibrium output y*, total demand Ey* equals output 0 y*.

IF ECONOMY PRODUCES AT A HIGHER LEVEL OF OUTPUT THAN EQUILIBRIUM • More goods and services are being produced than are desired by consumers and firms • Extra goods will pile up as demand fell short of production • Firms will react by cutting back on production • The economy rapidly adjusts to reach the equilibrium level of output

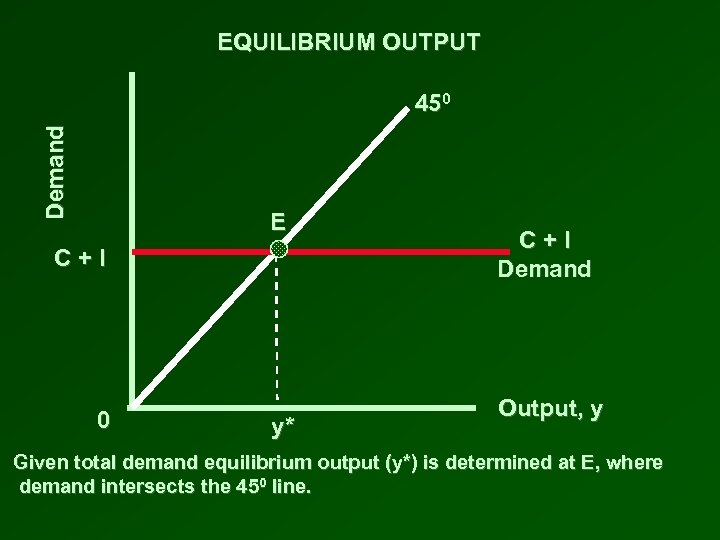EQUILIBRIUM OUTPUT Demand 450 E C+I 0 y* C+I Demand Output, y Given total demand equilibrium output (y*) is determined at E, where demand intersects the 450 line.

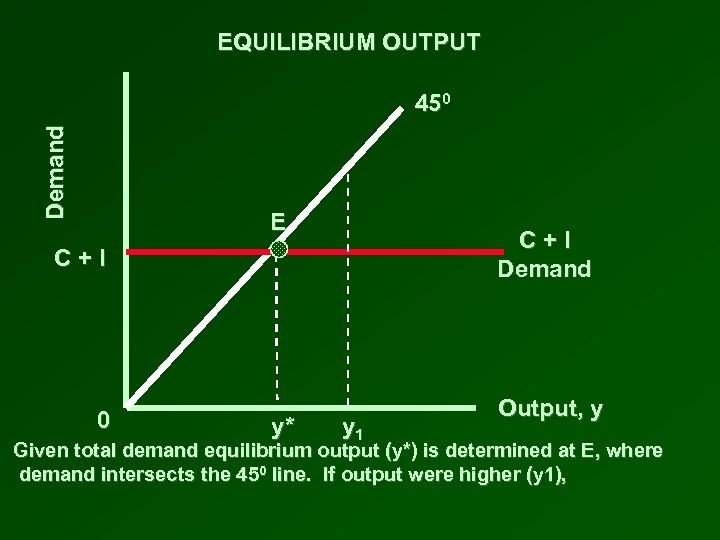EQUILIBRIUM OUTPUT Demand 450 E C+I Demand C+I 0 y* y 1 Output, y Given total demand equilibrium output (y*) is determined at E, where demand intersects the 450 line. If output were higher (y 1),

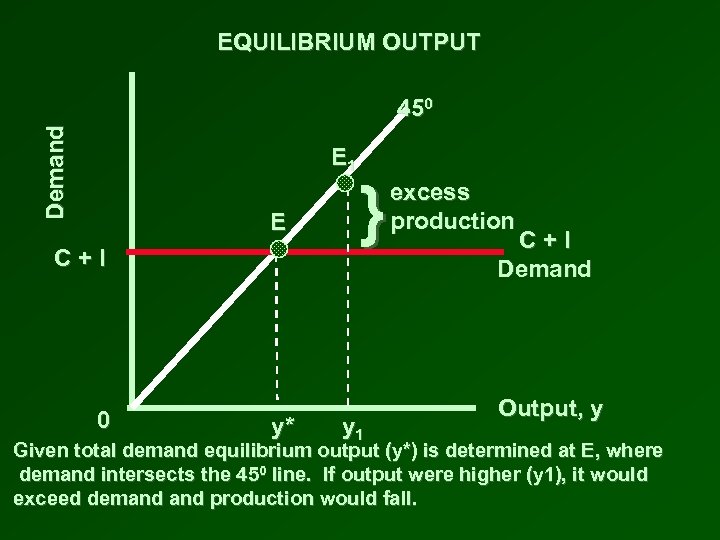EQUILIBRIUM OUTPUT Demand 450 E 1 E C+I 0 y* } y 1 excess production C+I Demand Output, y Given total demand equilibrium output (y*) is determined at E, where demand intersects the 450 line. If output were higher (y 1), it would exceed demand production would fall.

IF ECONOMY PRODUCES AT A LOWER LEVEL OF OUTPUT THAN EQUILIBRIUM • Demand would exceed total output • Firms find that demand for consumption and investment goods is greater that their current production • Inventories disappear and firms face increasing backlogs • Firms respond by stepping up production • The economy rapidly adjusts to reach the equilibrium level of output

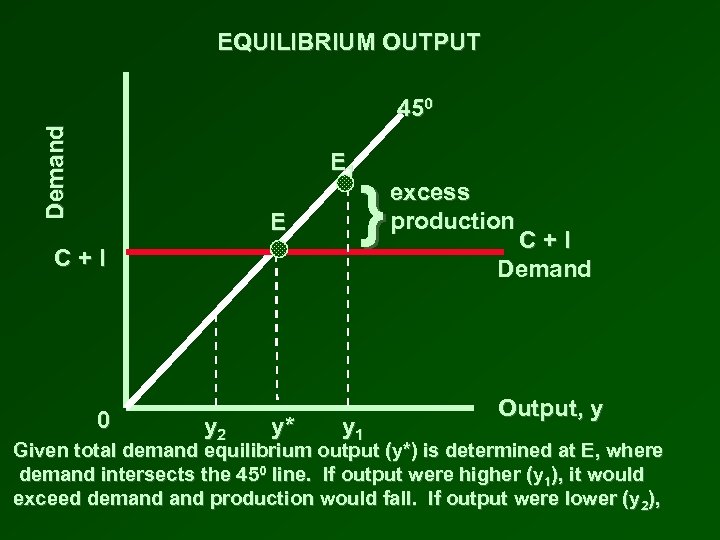EQUILIBRIUM OUTPUT Demand 450 E 1 E C+I 0 y 2 y* } y 1 excess production C+I Demand Output, y Given total demand equilibrium output (y*) is determined at E, where demand intersects the 450 line. If output were higher (y 1), it would exceed demand production would fall. If output were lower (y 2),

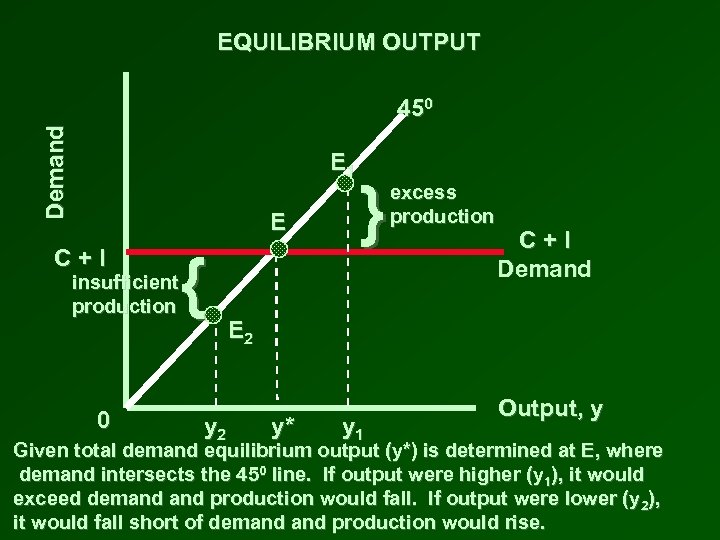EQUILIBRIUM OUTPUT Demand 450 E 1 E C+I insufficient production 0 { y 2 } excess production C+I Demand E 2 y* y 1 Output, y Given total demand equilibrium output (y*) is determined at E, where demand intersects the 450 line. If output were higher (y 1), it would exceed demand production would fall. If output were lower (y 2), it would fall short of demand production would rise.

THE CONSUMPTION FUNCTION • Describes the relationship between consumer spending and income C = Ca + by • Consumption spending, C, has two parts: – Ca = autonomous consumption is the part of total consumption which is unaffected by the level of income, i. e. it is constant at all levels of income. – by = the product of a fraction, b, called the marginal propensity to consume (MPC) and the level of income, y • The consumption function is a line that intersects the vertical axis at Ca. It has a slope equal to b.

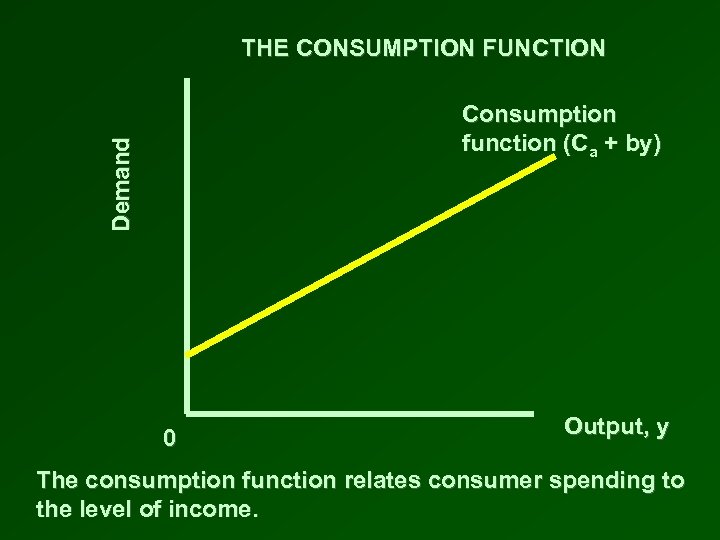THE CONSUMPTION FUNCTION Demand Consumption function (Ca + by) 0 Output, y The consumption function relates consumer spending to the level of income.

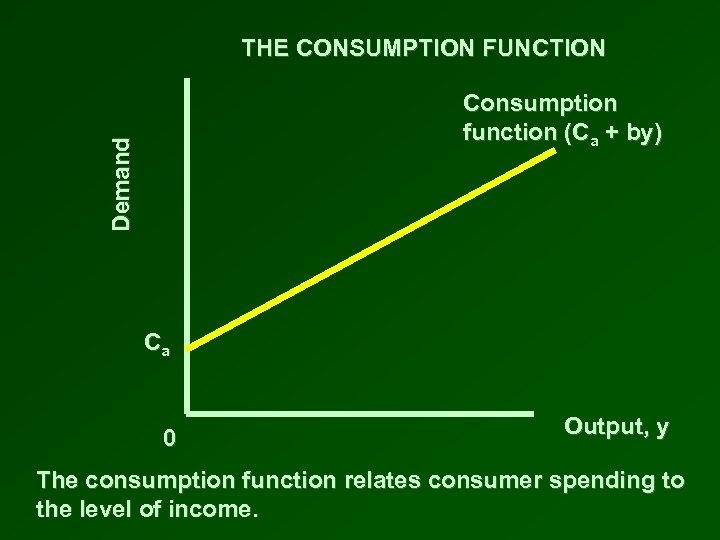THE CONSUMPTION FUNCTION Demand Consumption function (Ca + by) Ca 0 Output, y The consumption function relates consumer spending to the level of income.

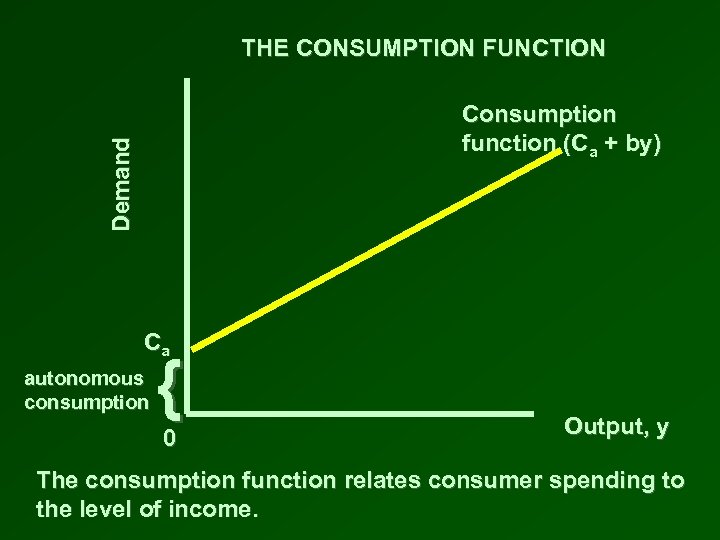THE CONSUMPTION FUNCTION Demand Consumption function (Ca + by) Ca autonomous consumption { 0 Output, y The consumption function relates consumer spending to the level of income.

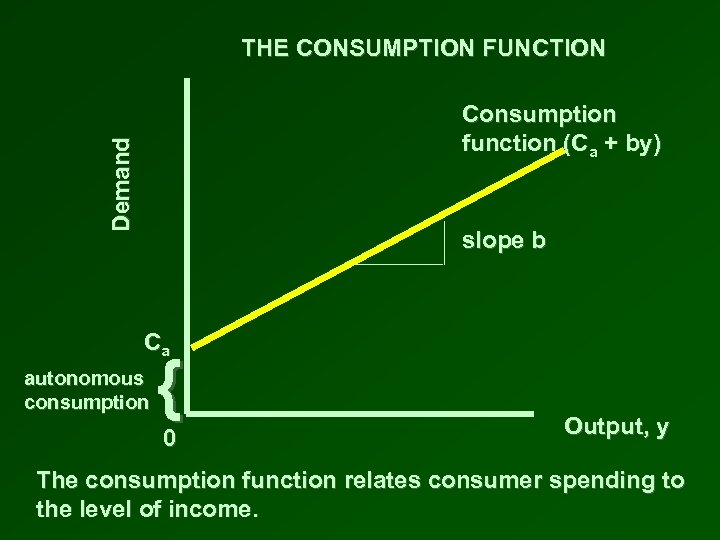THE CONSUMPTION FUNCTION Demand Consumption function (Ca + by) slope b Ca autonomous consumption { 0 Output, y The consumption function relates consumer spending to the level of income.

THE CONSUMPTION FUNCTION • Although output is on the horizontal axis, output and income in this simple economy are identical • Output generates income that is all received by households • As output rises by $1, consumption increases by the marginal propensity to consume (b) times $1

MARGINAL PROPENSITY TO CONSUME (MPC) • Is always less than 1 • If a consumer receives a dollar of income, consumer will spend some of it and save the rest • The fraction that the consumer spends is determined by the MPC • The fraction of income that the consumer saves is determined by the marginal propensity to save (MPS) • The sum of the MPC and MPS is always 1 $$ $$

CHANGES IN THE CONSUMPTION FUNCTION • The level of autonomous consumption and the MPC can change causing movements in the consumption function • If the level of autonomous consumption is higher, it will shift the entire consumption function. • Changes in the marginal propensity to consume will change the slope of the consumption function.

AUTONOMOUS CONSUMPTION CHANGES • Increases in consumer wealth will cause an increase in autonomous consumption Consumer wealth consists of the value of stocks, bonds and consumer durables • Increases in consumer confidence will increase autonomous consumption

Demand MOVEMENTS OF THE CONSUMPTION FUNCTION C a 0 Output, y

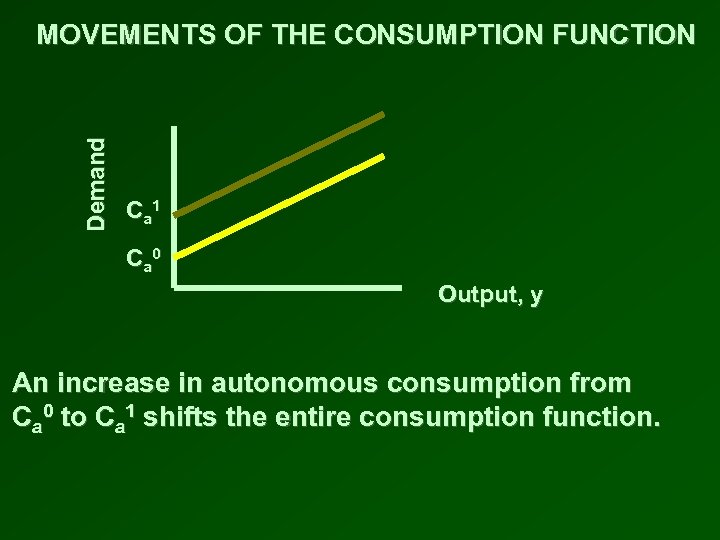Demand MOVEMENTS OF THE CONSUMPTION FUNCTION C a 1 C a 0 Output, y An increase in autonomous consumption from Ca 0 to Ca 1 shifts the entire consumption function.

MARGINAL PROPENSITY TO CONSUME CHANGES • Consumers’ perceptions of changes in their income affect their MPC • If consumers believe that an increase in their income is permanent, they will consume a higher fraction of the increased income than if the increase were believed to be temporary $$

Demand MOVEMENTS OF THE CONSUMPTION FUNCTION Slope b Output, y

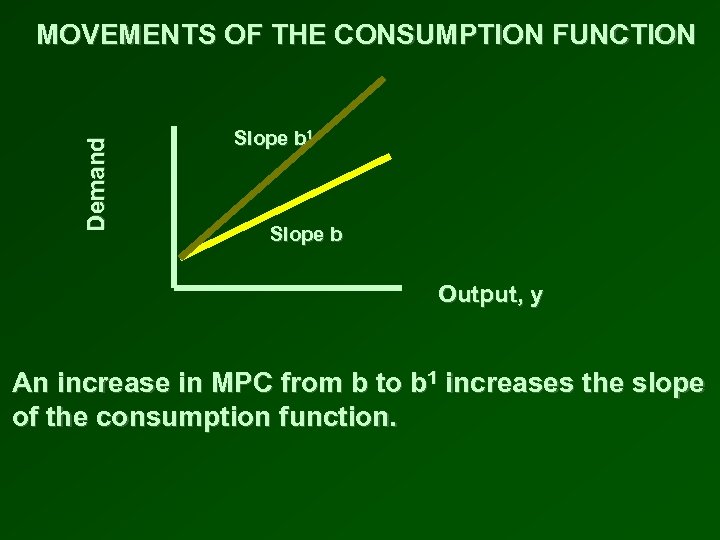Demand MOVEMENTS OF THE CONSUMPTION FUNCTION Slope b 1 Slope b Output, y An increase in MPC from b to b 1 increases the slope of the consumption function.

DETERMINING GDP • Plot the consumption function • Investment is constant at all levels of income • Add the level of desired investment vertically to the consumption function • The C + I line is the total spending in the economy • At any level of income, total spending is C + I • The level of equilibrium income, y*, occurs where the total spending ( C + I ) line crosses the 450 line • At this level of output, total spending equals output

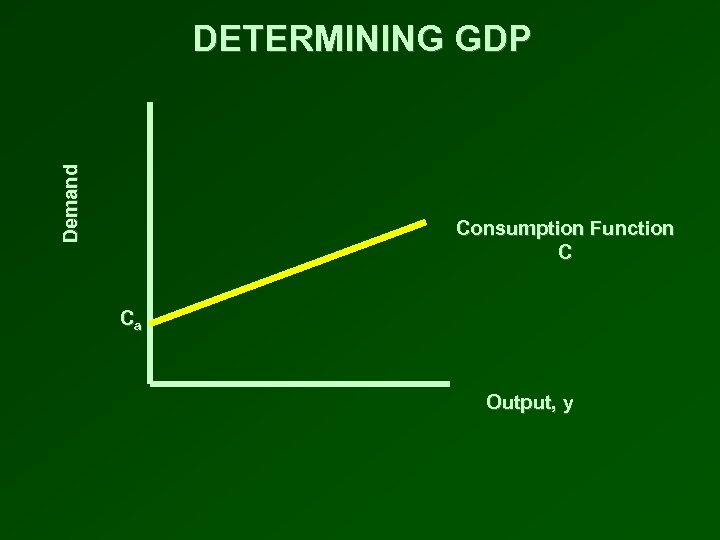Demand DETERMINING GDP Consumption Function C Ca Output, y

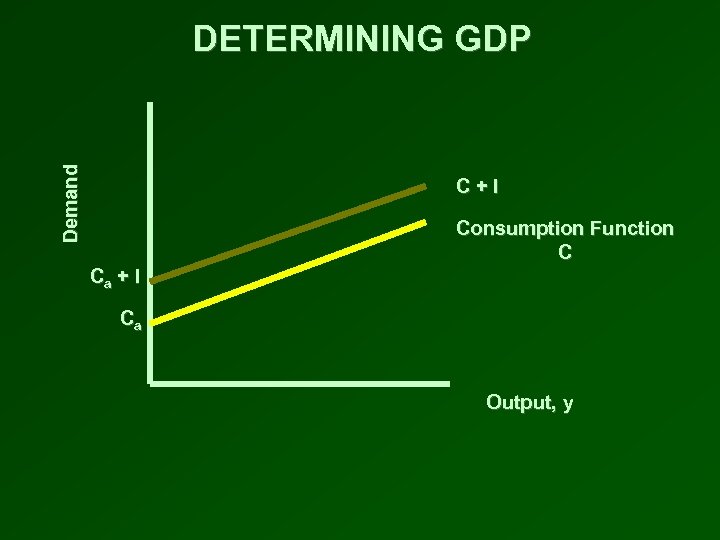Demand DETERMINING GDP C+I Consumption Function C Ca + I Ca Output, y

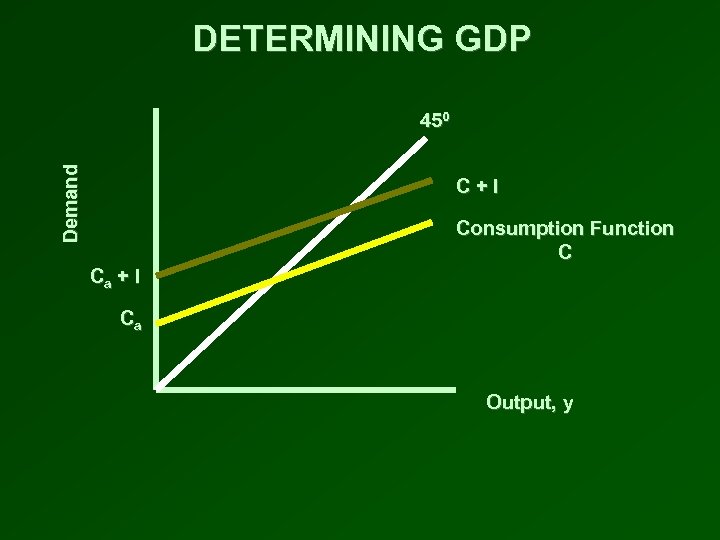DETERMINING GDP Demand 450 C+I Consumption Function C Ca + I Ca Output, y

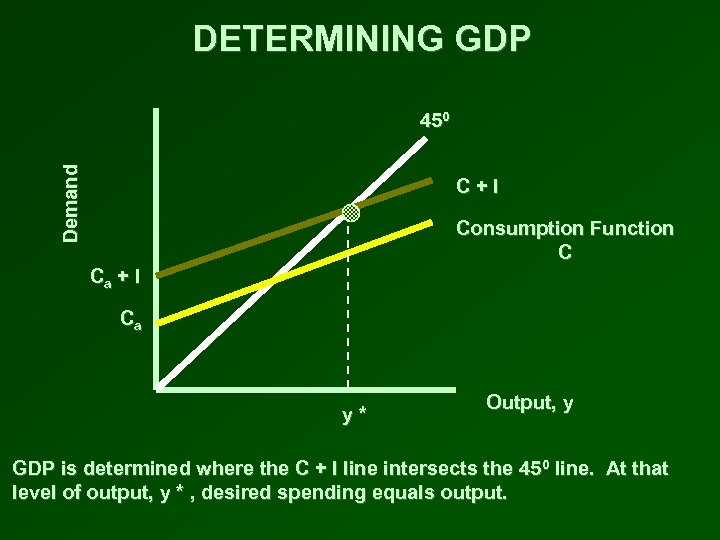DETERMINING GDP Demand 450 C+I Consumption Function C Ca + I Ca y* Output, y GDP is determined where the C + I line intersects the 450 line. At that level of output, y * , desired spending equals output.

EQUILIBRIUM INCOME • • • = autonomous consumption / (1 - MPC) Y * = (Ca + I) / (1 - b) Suppose : C = 100 + 0. 6 Ca = 100 b = 0. 6 I = 40 Using the formula for equilibrium income: Y * = (100 + 40) / (1 - 0. 6) Y * = 140 / 0. 4 y * = 350 In equilibrium, saving = investment

THE MULTIPLIER The increase in output divided by an increase investment • An increase in investment spending shifts up the C + I curve by I • The intersection with the 450 line shifts from E 0 to E 1 • GDP increases by y from y 0 to y 1 • The increase in GDP (y) is greater than the increase in investment (I) • Since output increases more than the initial increase in investment, the multiplier is greater than 1

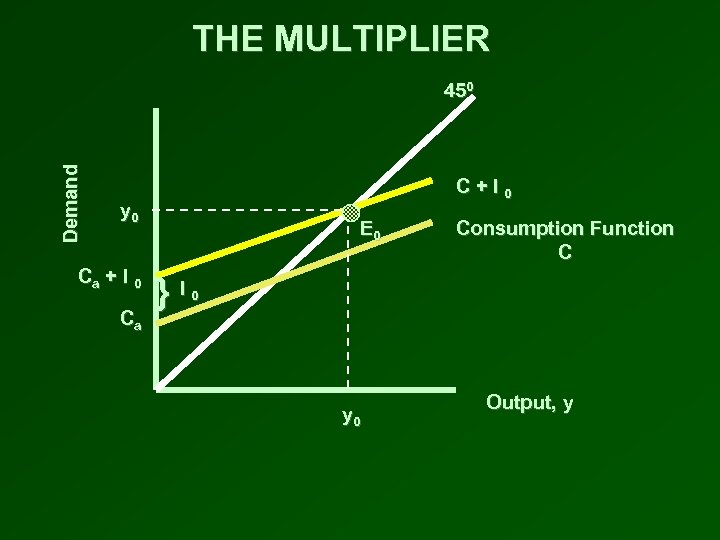THE MULTIPLIER Demand 450 C+I 0 y 0 Ca + I 0 Ca E 0 }I Consumption Function C 0 y 0 Output, y

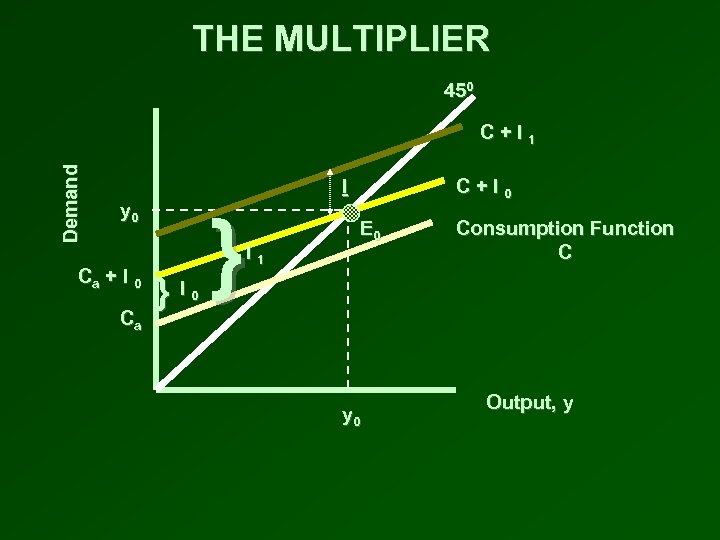THE MULTIPLIER 450 Demand C+I 1 I y 0 Ca + I 0 Ca } I 1 } I 0 C+I 0 E 0 y 0 Consumption Function C Output, y

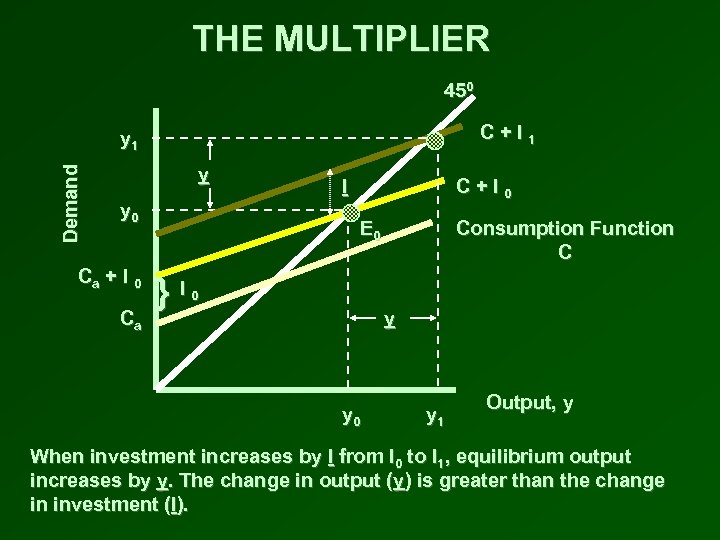THE MULTIPLIER 450 C+I 1 Demand y 1 y y 0 Ca + I 0 Ca I C+I 0 E 0 }I Consumption Function C 0 y y 0 y 1 Output, y When investment increases by I from I 0 to I 1, equilibrium output increases by y. The change in output (y) is greater than the change in investment (I).

KEYNESIAN FISCAL POLICY Using taxes and spending to influence the level of GDP in the short run GDP Taxes & Spending

GOVERNMENT SPENDING • Government purchases of goods and services ( G ) is a component of spending • Total spending is C + I + G • Increases of government purchases ( G ) shift up the C + I + G line just as increases of investment spending or autonomous consumption spending do • The multiplier for government spending is also the same as for changes in investment or autonomous consumption

GOVERNMENT SPENDING • Changes in government purchases have exactly the same effects as changes in investment spending or autonomous consumption spending • The multiplier for government spending is also the same as for changes in investment or autonomous consumption Multiplier for government spending = 1 / (1 -MPC)

DISPOSABLE PERSONAL INCOME The income that ultimately flows back to households and consumers, after subtracting any taxes that are paid and after adding any transfer payments received by households (such as social security, unemployment insurance and welfare) disposable Personal income = (y-T) where T is net taxes -- taxes minus transfer payments

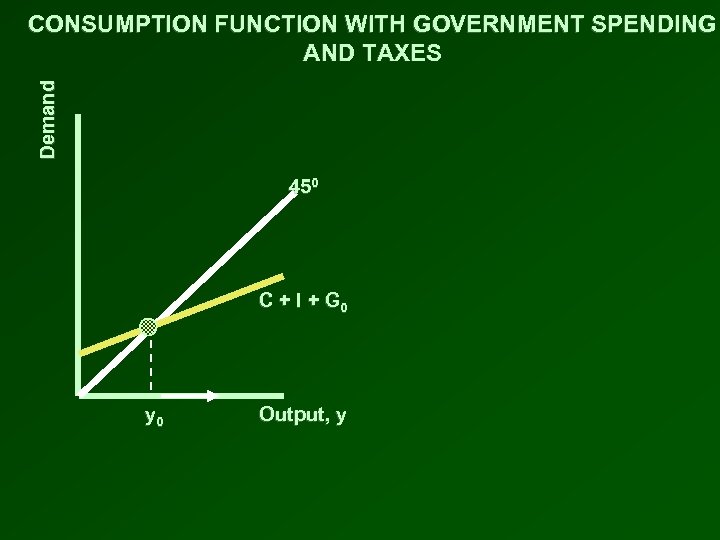Demand CONSUMPTION FUNCTION WITH GOVERNMENT SPENDING AND TAXES 450 C + I + G 0 y 0 Output, y

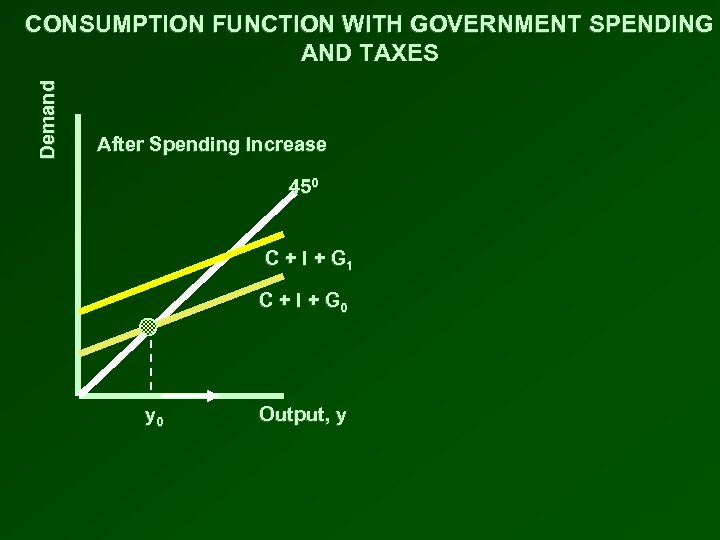Demand CONSUMPTION FUNCTION WITH GOVERNMENT SPENDING AND TAXES After Spending Increase 450 C + I + G 1 C + I + G 0 y 0 Output, y

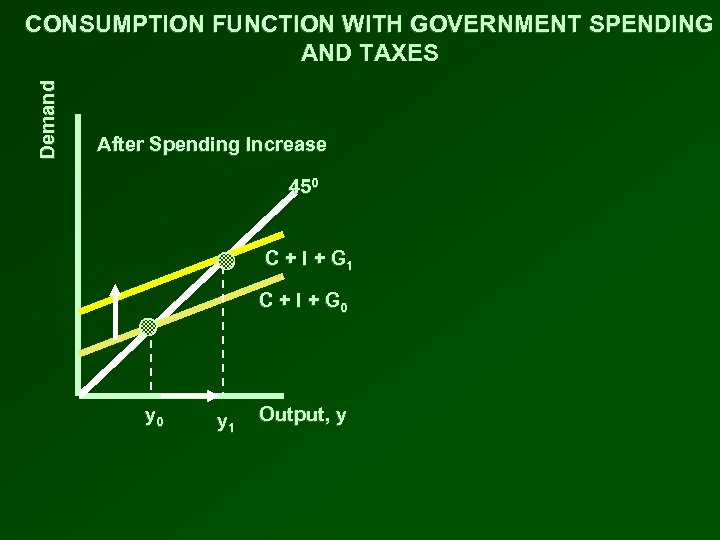Demand CONSUMPTION FUNCTION WITH GOVERNMENT SPENDING AND TAXES After Spending Increase 450 C + I + G 1 C + I + G 0 y 1 Output, y

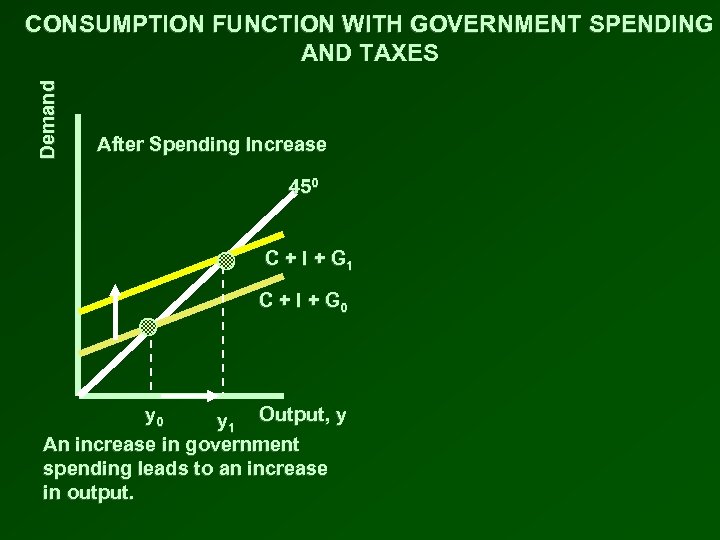Demand CONSUMPTION FUNCTION WITH GOVERNMENT SPENDING AND TAXES After Spending Increase 450 C + I + G 1 C + I + G 0 y 1 Output, y An increase in government spending leads to an increase in output.

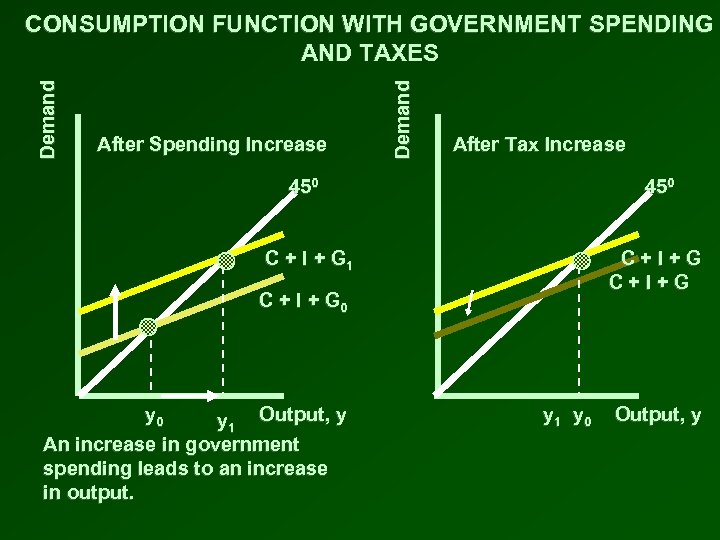After Spending Increase Demand CONSUMPTION FUNCTION WITH GOVERNMENT SPENDING AND TAXES After Tax Increase 450 C + I + G 1 C+I+G C + I + G 0 y 1 Output, y An increase in government spending leads to an increase in output. y 1 y 0 Output, y

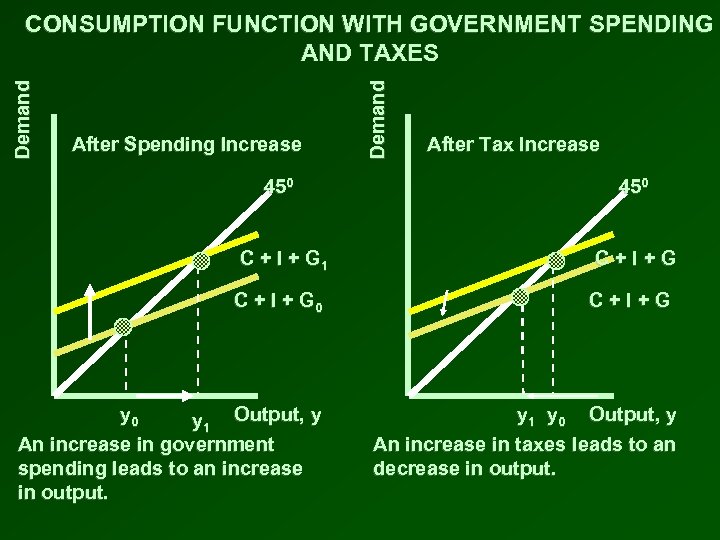After Spending Increase Demand CONSUMPTION FUNCTION WITH GOVERNMENT SPENDING AND TAXES After Tax Increase 450 C + I + G 1 C+I+G C + I + G 0 C+I+G y 0 y 1 Output, y An increase in government spending leads to an increase in output. y 1 y 0 Output, y An increase in taxes leads to an decrease in output.

TAX MULTIPLIER • Is negative because increases in taxes decrease disposable income and lead to reduction in consumption spending • Is smaller (in absolute value) than the government spending multiplier, because an increase in taxes first reduces the disposable income of households by the amount of the tax • tax multiplier = - b / (1 - b) = - MPC / ( 1 - MPC )

BALANCED-BUDGET MULTIPLIER • The multiplier for equal increases in government spending and taxes • Equal increases in spending and taxes will not unbalance the budget • Is always equal to “ 1”

EXPANSIONARY POLICIES Government policies that increase total demand GDP. • Tax cuts and spending increases are examples of expansionary policies

CONTRACTIONARY POLICIES Government policies that decrease total demand GDP. • Tax increases and spending cuts are examples of contractionary policies.

BUDGET DEFICIT Increases when government increases spending or cuts taxes to stimulate the economy.

PERMANENT INCOME Consumers often base their spending on an estimate of their long-run average income.

AUTOMATIC STABILIZERS Taxes and transfers which act as economic institutions that automatically reduce economic fluctuations.

HOW AUTOMATIC STABILIZERS WORK • When income is high: -- government collects more taxes and pays out less transfer payments -- since government is taking funds from consumers, this tends to reduce consumer spending • When income is low (i. e. , during recessions): -- government collects less taxes and pays out more transfer payments -- tends to increase consumer spending, since the government is putting funds into the hands of consumers

AFTER A TAX INCREASE • Consumption function depends on after-tax income: C = Ca + b ( 1 - t ) y • Marginal propensity to consume is now adjusted for taxes and becomes b(1 -t) • Raising the tax rate therefore lowers the MPC adjusted for taxes

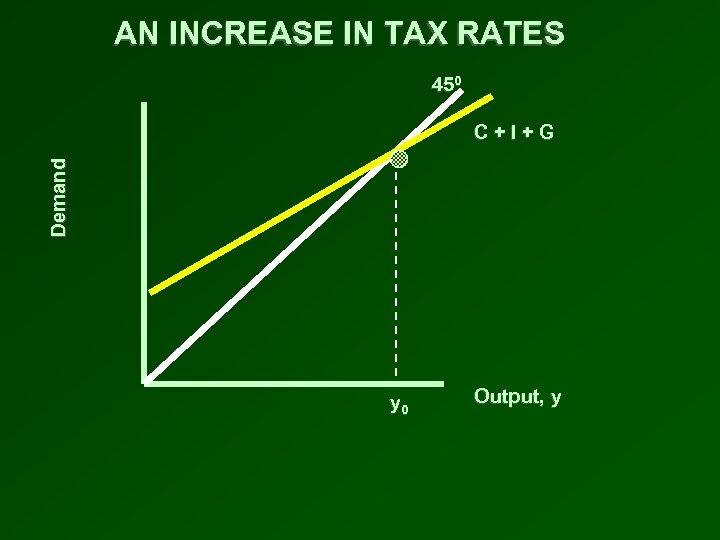AN INCREASE IN TAX RATES 450 Demand C+I+G y 0 Output, y

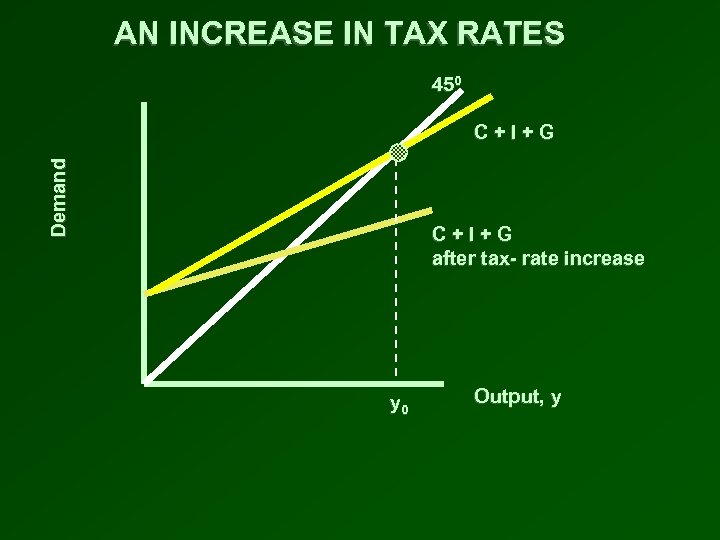AN INCREASE IN TAX RATES 450 Demand C+I+G after tax- rate increase y 0 Output, y

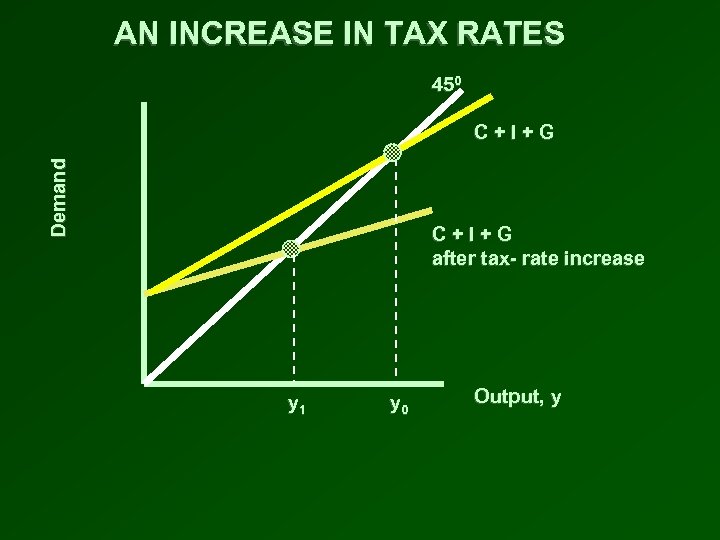AN INCREASE IN TAX RATES 450 Demand C+I+G after tax- rate increase y 1 y 0 Output, y

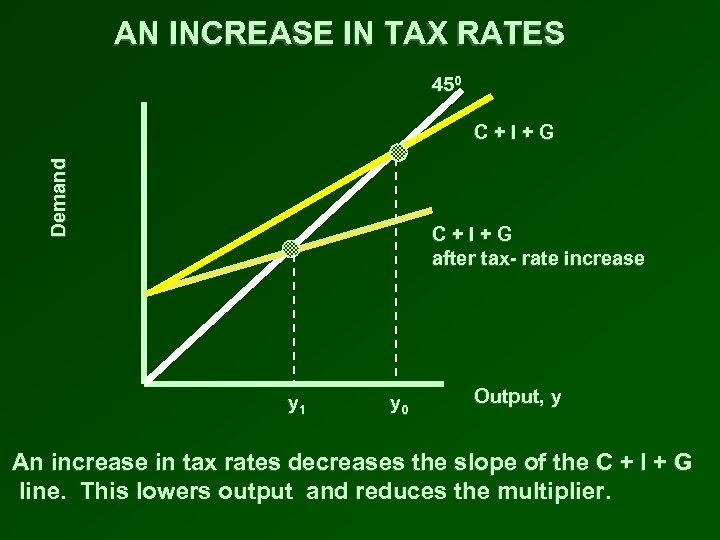AN INCREASE IN TAX RATES 450 Demand C+I+G after tax- rate increase y 1 y 0 Output, y An increase in tax rates decreases the slope of the C + I + G line. This lowers output and reduces the multiplier.

OTHER FACTORS CONTRIBUTING TO STABILITY OF ECONOMY • If households base their consumption decisions partly on their permanent or longrun income, they will not be very sensitive to changes in current income. • If consumption doesn’t change much with current income, the marginal propensity to consume out of current income will be small, which will make the multiplier small. • When consumers base their decisions on long -run factors, not just on their current level of income, the economy tends to be stabilized.

MODIFYING THE MODEL FOR EXPORTS AND IMPORTS • Add exports, X, as another source of demand for US goods and services • Subtract imports, M, from the total spending by US residents • Consumers will import more goods as income rises: imports = M = m*y • m is the fraction known as the marginal propensity to import • Subtract this fraction from the overall marginal propensity to consume ( b ) to obtain the MPC for spending on domestic goods

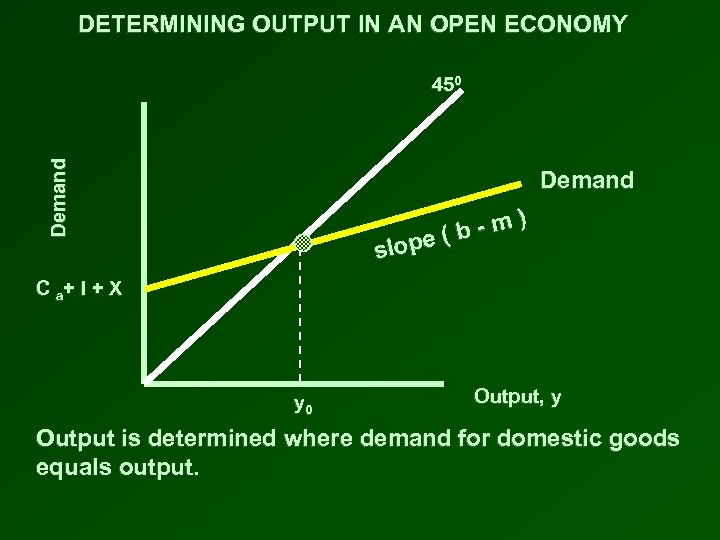DETERMINING OUTPUT IN AN OPEN ECONOMY Demand 450 Demand -m) (b lo pe s C a+ I + X y 0 Output, y Output is determined where demand for domestic goods equals output.

Demand INCREASE IN EXPORTS AND IMPORTS 450 Ca + I + X 450 y 0 Output, y

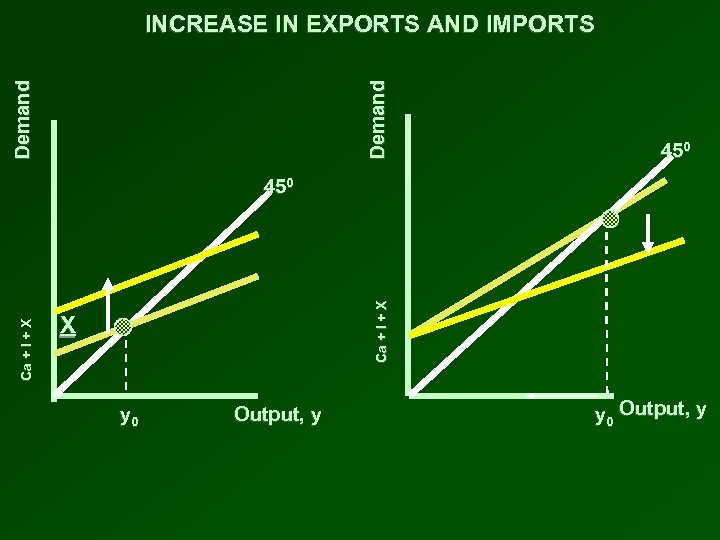Demand INCREASE IN EXPORTS AND IMPORTS 450 Ca + I + X 450 X y 0 Output, y

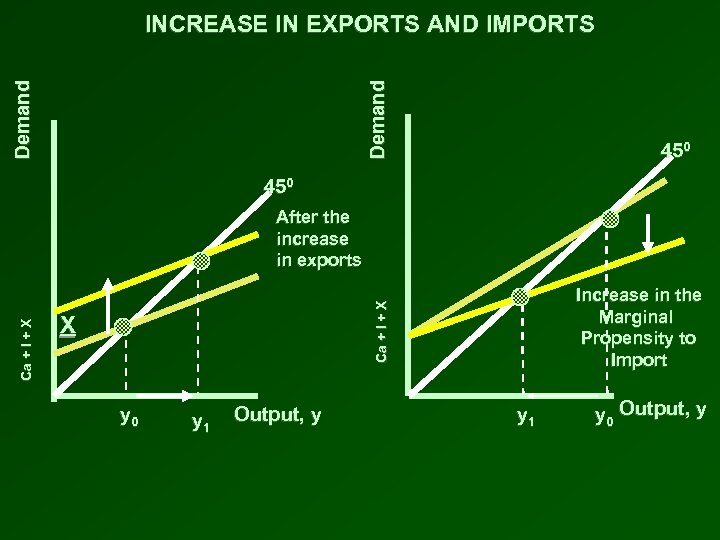Demand INCREASE IN EXPORTS AND IMPORTS 450 Increase in the Marginal Propensity to Import Ca + I + X After the increase in exports X y 0 y 1 Output, y y 1 y 0 Output, y

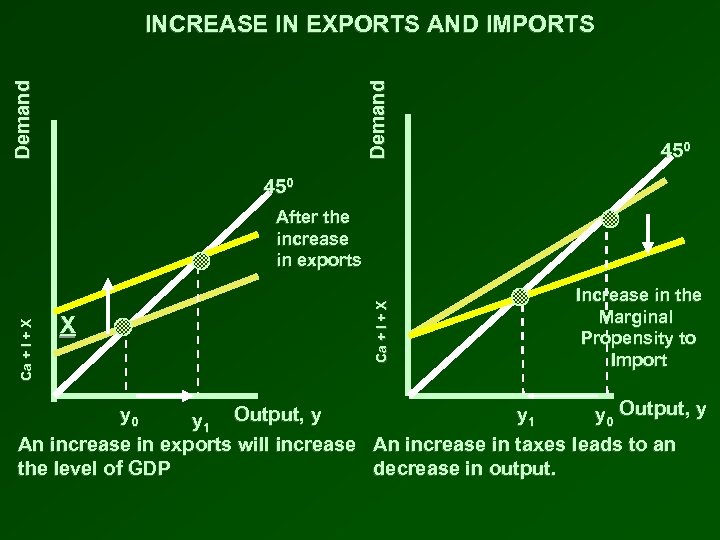Demand INCREASE IN EXPORTS AND IMPORTS 450 X y 0 y 1 Output, y An increase in exports will increase the level of GDP Ca + I + X After the increase in exports Increase in the Marginal Propensity to Import y 1 y 0 Output, y An increase in taxes leads to an decrease in output.

ACTUAL VERSUS PLANNED - 1 • A firm may not always invest the exact amount that it planned to. • Why? • Firms do not have complete control over their investment decisions. • This is not true of consumption, as households have complete control over their consumption. Planned consumption is always equal to actual consumption.

ACTUAL VERSUS PLANNED - 2 • Firms can generally chose how much new plant and equipment they wish to purchase in any given period (e. g. Mc. Donald’s buys an extra french-fry machines, etc). • However, firms have less control over inventory investment. • Remember, inventories are part of the capital stock. Manufacturing firms have two kind of inventories: – Inputs (e. g. tyres, rolled steel, engine blocks, etc) – Final production (finished automobiles awaiting shipment)

ACTUAL VERSUS PLANNED - 3 • Consequently, one component of investment inventory change - is partly determined by how much households decide to buy, which is not under complete control of firms. • If households do not buy as much as firms expect them to, inventories will be higher than expected, and firms will have made an inventory investment that they did not plan to make.

ACTUAL VERSUS PLANNED - 4 • Because involuntary inventory adjustments are neither desired nor planned, we need to distinguish between actual investment and desired , or planned investment. • When we have been discussing I in this lecture, we have used I to refer to desired or planned investment only. • So, we could have written: Planned aggregate expenditure AE Consumption + Planned investment C+I

EQUILBIRUM AGGREGATE OUTPUT (INCOME) - 1 • In microeconomics we said that equilibrium is said to exist in a particular market (e. g. the market for bananas) at the price for which the quantity demanded is equal to the quantity supplied. • In macroeconomics, we define equilibrium in the goods market as that point at which planned aggregate expenditure is equal to aggregate output.

EQUILBIRUM AGGREGATE OUTPUT (INCOME) - 2 Aggregate output Y Planned aggregate expenditure AE C + I Equilibrium: Y = AE, or Y = C + I • This definition of equilibrium can hold if, and only if, planned investment and actual investment are equal. To understand why, consider Y no equal to AE. First let us suppose aggregate output is greater than planned aggregate expenditure: Y>C + I Aggregate output> Planned aggregate expenditure

EQUILBIRUM AGGREGATE OUTPUT (INCOME) - 3 • When output is greater than planned spending, there is unplanned inventory investment. Firms planned to sell more of their goods than they sold, and the difference shows up as unplanned increase in inventories. • Suppose now that planned aggregate expenditure is greater than aggregate output: C+I>Y Planned aggregate expenditure > Aggregate output

EQUILBIRUM AGGREGATE OUTPUT (INCOME) - 4 • When planned spending exceeds output, firms have sold more than they planned to. Inventory investment is smaller than planned. • Planned and actual investment are not equal. Only when output is exactly matched by planned spending will there be no unplanned inventory investment. • Equilibrium in the goods market is achieved only when aggregate output (Y) and planned aggregate expenditure (C+I) are equal, or when actual and planned investment are equal.

SAVINGS AND INVESMENT APPROACH - 1 • Because aggregate income must either be saved or spent, by definition: Y C+S THIS IS AN IDENTITY • The equilibrium condition is: Y=C+I BUT THIS IS NOT AN IDENTITY, BECAUSE IT DOES NOT HOLD WHEN WE ARE OUT OF EQUILIBRIUM. IT WOULD BE AN IDENTITY IF I WERE ACTUAL INVESTMENT RATHER THAN PLANNED INVESTMENT

SAVINGS AND INVESMENT APPROACH - 2 • Substituting C + S for Y in the equilibrium condition, we can write: Saving/investment approach to equilibrium: C + S = C + I Because we can subtract C from both sides of this equation, we are left with S = I. Thus, only when planned investment equals saving will there be equilibrium. • Remember, saving is income that is not spent. Because it is not spent, saving is like a leakage out of the spending stream.

SAVINGS AND INVESMENT APPROACH - 3 • Only if that leakage is counterbalanced by some other component of planned spending can the resulting planned aggregate expenditure equal aggregate output. This other component is planned investment (I). • The leakage out of the spending stream - saving is matched by an equal injection of planned investment spending into the spending stream. • For this reason, the saving/investment approach to equilibrium is also called the leakages/ injections approach to equilibrium.