Lecture 5 FCS Autocorrelation PCH Cross -correlation Enrico

Lecture 5 FCS, Autocorrelation, PCH, Cross -correlation Enrico Gratton Principles of Fluorescence Techniques Laboratory for Fluorescence Dynamics

Fluorescence Parameters & Methods 1. Excitation & Emission Spectra • Local environment polarity, fluorophore concentration 2. Anisotropy & Polarization • Rotational diffusion 3. Quenching • Solvent accessibility • Character of the local environment 4. Fluorescence Lifetime • Dynamic processes (nanosecond timescale) 5. Resonance Energy Transfer • Probe-to-probe distance measurements 6. Fluorescence microscopy • localization 7. Fluorescence Correlation Spectroscopy • Translational & rotational diffusion • Concentration • Dynamics

First Application of Correlation Spectroscopy (Svedberg & Inouye, 1911) Occupancy Fluctuation Experimental data on colloidal gold particles: 120002001324123102111131125111023313332211122422122612214 2345241141311423100100421123123201111000111_2110013200000 1001100023221002110000201001_333122000231221024011102_ 1222112231000110331110210110010103011312121010121111211_10 003221012302012121321110110023312242110001203010100221734 410101002112211444421211440132123314313011222123310121111 222412231113322132110000410432012120011322231200_253212033 2331111002201301132111312001013143221122323442230 321421532200202142123232043112312003314223452134110412322 220221 Collected data by counting (by visual inspection) the number of particles in the observation volume as a function of time using a “ultra microscope”

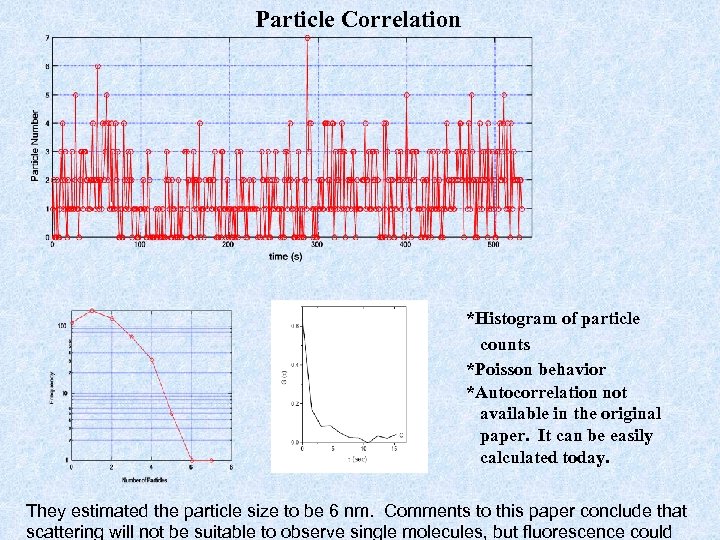Particle Correlation *Histogram of particle counts *Poisson behavior *Autocorrelation not available in the original paper. It can be easily calculated today. They estimated the particle size to be 6 nm. Comments to this paper conclude that scattering will not be suitable to observe single molecules, but fluorescence could

In FCS Fluctuations are in the Fluorescence Signal Diffusion Enzymatic Activity Phase Fluctuations Conformational Dynamics Rotational Motion Protein Folding Example of processes that could generate fluctuations

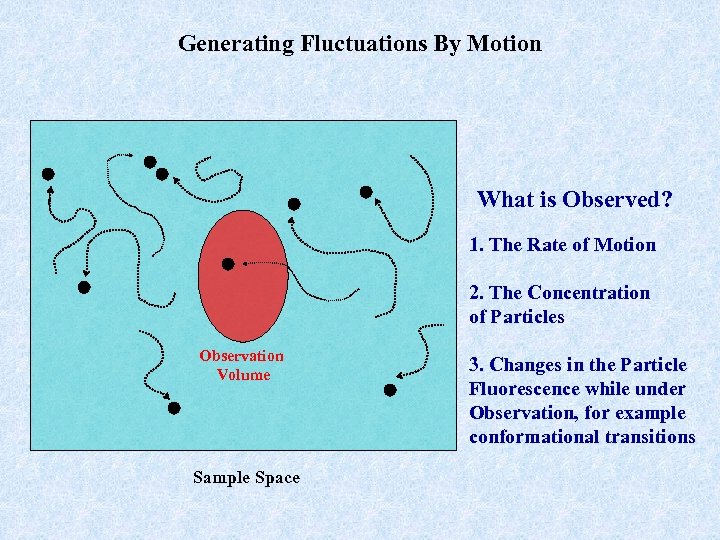Generating Fluctuations By Motion What is Observed? 1. The Rate of Motion 2. The Concentration of Particles Observation Volume Sample Space 3. Changes in the Particle Fluorescence while under Observation, for example conformational transitions

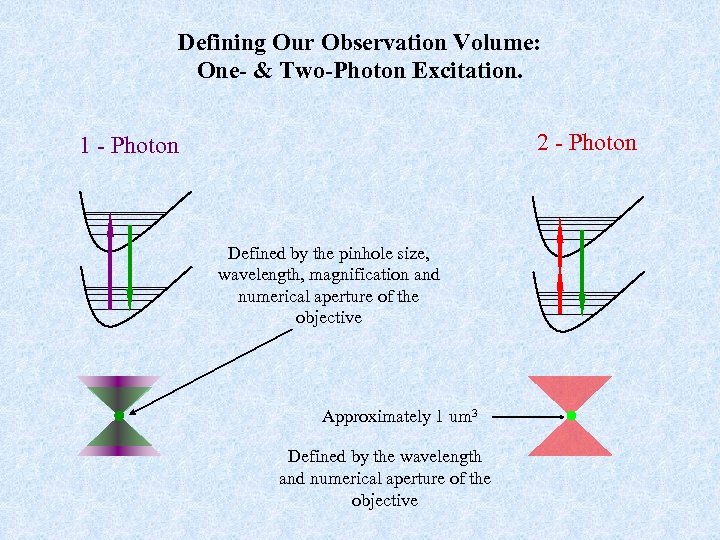Defining Our Observation Volume: One- & Two-Photon Excitation. 2 - Photon 1 - Photon Defined by the pinhole size, wavelength, magnification and numerical aperture of the objective Approximately 1 um 3 Defined by the wavelength and numerical aperture of the objective

1 -photon Need a pinhole to define a small volume 2 -photon Brad Amos MRC, Cambridge, UK

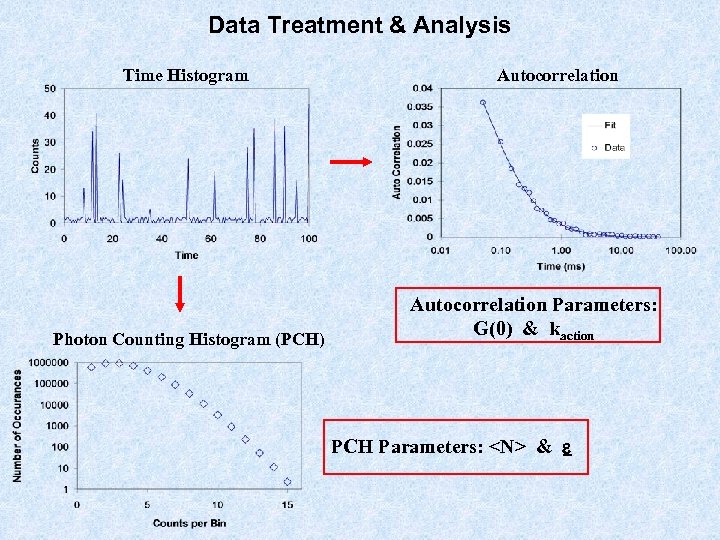Data Treatment & Analysis Time Histogram Photon Counting Histogram (PCH) Autocorrelation Parameters: G(0) & kaction PCH Parameters: & e

Autocorrelation Function Factors influencing the fluorescence signal: k. Q = quantum yield and detector sensitivity (how bright is our probe). This term could contain the fluctuation of the fluorescence intensity due to internal processes W(r) describes our observation volume C(r, t) is a function of the fluorophore concentration over time. This is the term that contains the “physics” of the diffusion processes

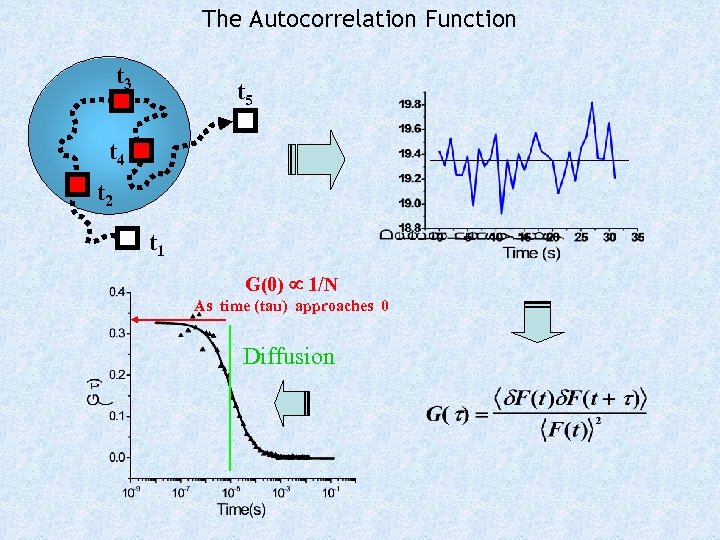The Autocorrelation Function t 3 t 5 t 4 t 2 t 1 G(0) 1/N As time (tau) approaches 0 Diffusion

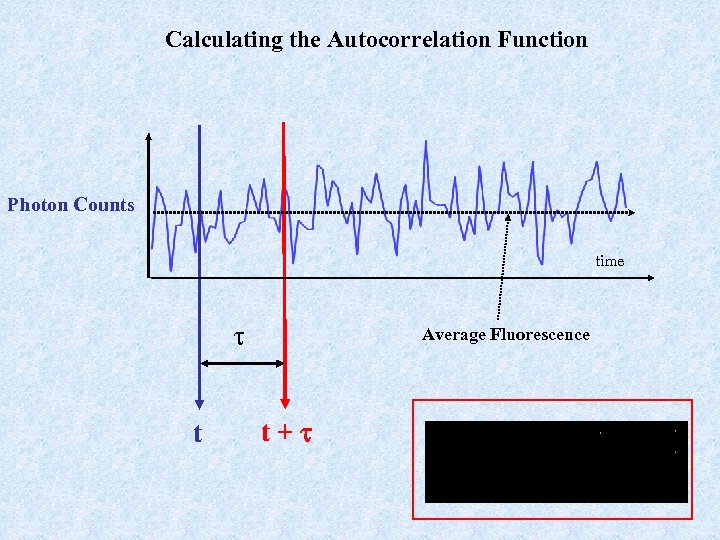Calculating the Autocorrelation Function Photon Counts time t Average Fluorescence t+t

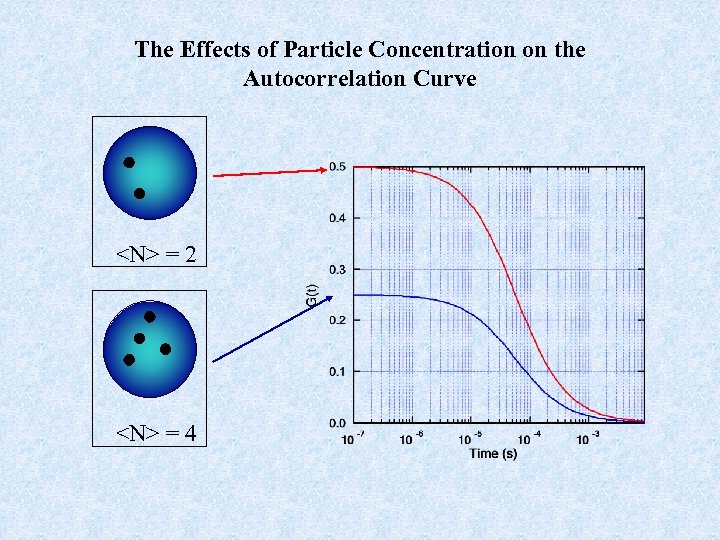The Effects of Particle Concentration on the Autocorrelation Curve = 2 = 4

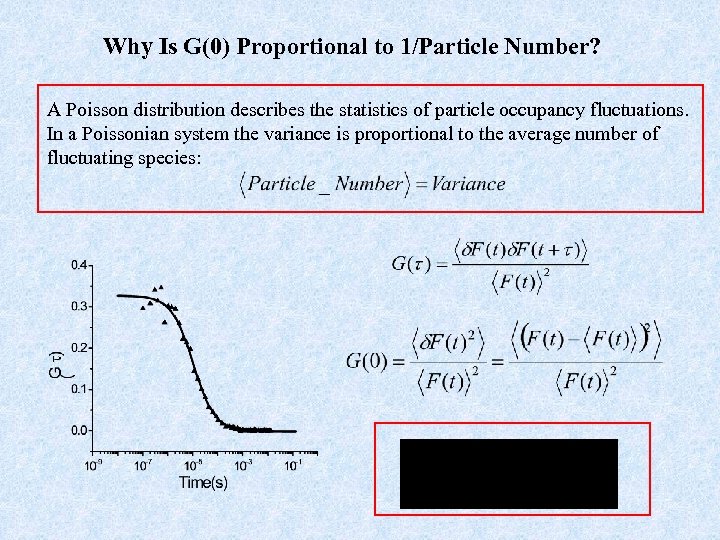Why Is G(0) Proportional to 1/Particle Number? A Poisson distribution describes the statistics of particle occupancy fluctuations. In a Poissonian system the variance is proportional to the average number of fluctuating species:

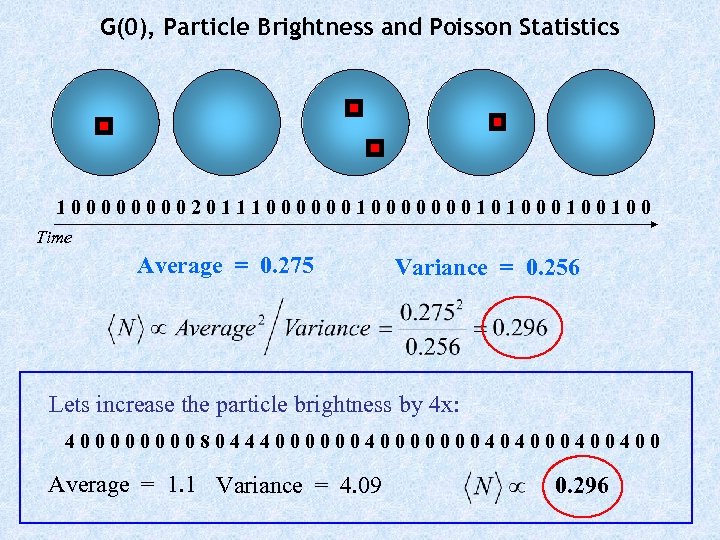G(0), Particle Brightness and Poisson Statistics 1000020111000000010100100 Time Average = 0. 275 Variance = 0. 256 Lets increase the particle brightness by 4 x: 4000080444000000040400400 Average = 1. 1 Variance = 4. 09 0. 296

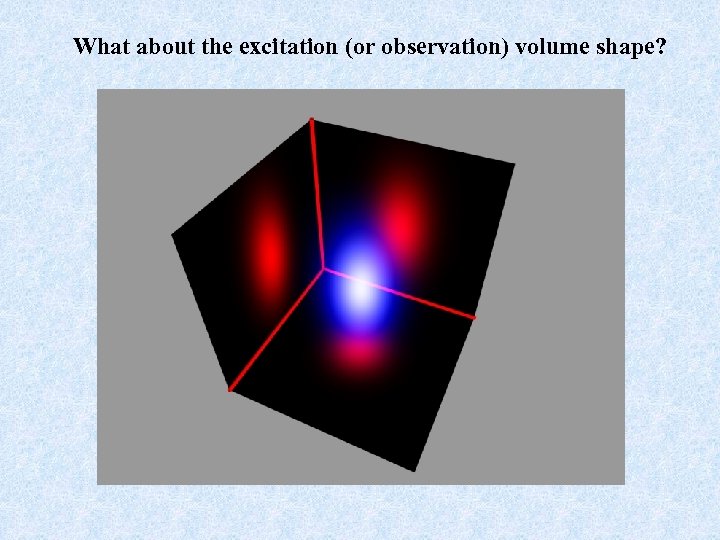What about the excitation (or observation) volume shape?

Effect of Shape on the (Two-Photon) Autocorrelation Functions: For a 2 -dimensional Gaussian excitation volume: 1 -photon equation contains a 4, instead of 8 For a 3 -dimensional Gaussian excitation volume:

Additional Equations: 3 D Gaussian Confocor analysis: . . . where N is the average particle number, t. D is the diffusion time (related to D, t. D=w 2/8 D, for two photon and t. D=w 2/4 D for 1 -photon excitation), and S is a shape parameter, equivalent to w/z in the previous equations. Triplet state term: . . where T is the triplet state amplitude and t. T is the triplet lifetime.

Orders of magnitude (for 1 μM solution, small molecule, water) Volume Device Size(μm) Molecules millilitercuvette 10000 6 x 1014 104 microliter plate well 1000 6 x 1011 nanoliter microfabrication 100 6 x 108 picoliter typical cell 10 6 x 105 femtoliter confocal volume 1 6 x 102 attoliter nanofabrication 0. 1 6 x 10 -1 Time 102 1 10 -2 10 -4 10 -6

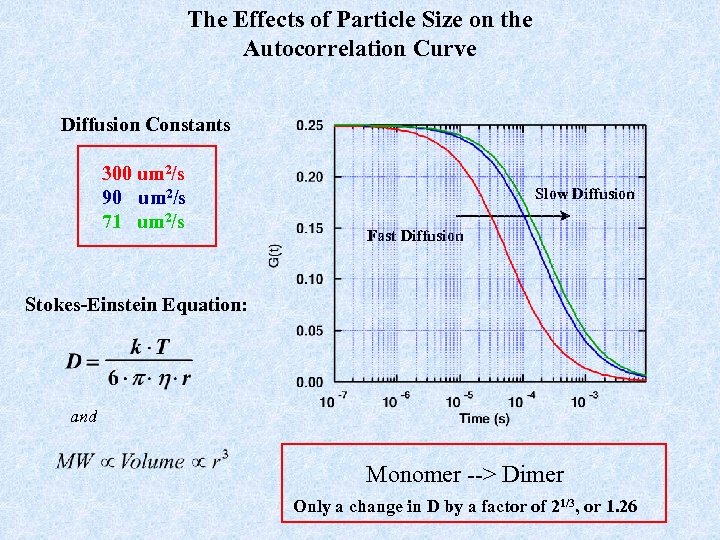The Effects of Particle Size on the Autocorrelation Curve Diffusion Constants 300 um 2/s 90 um 2/s 71 um 2/s Slow Diffusion Fast Diffusion Stokes-Einstein Equation: and Monomer --> Dimer Only a change in D by a factor of 21/3, or 1. 26

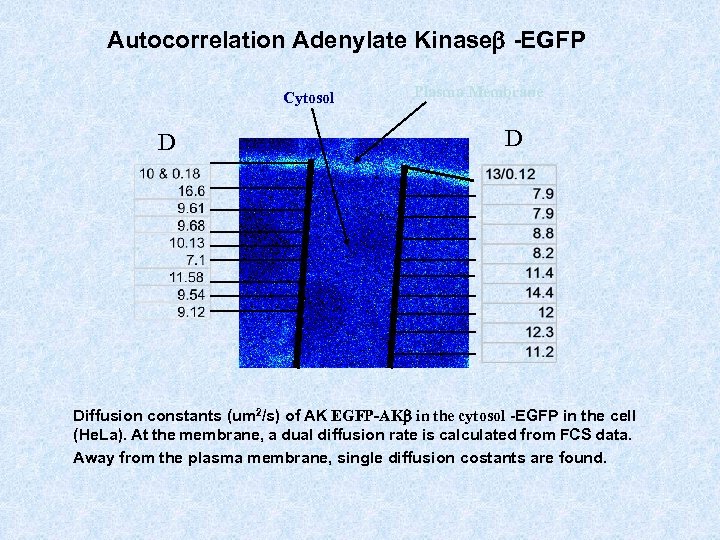
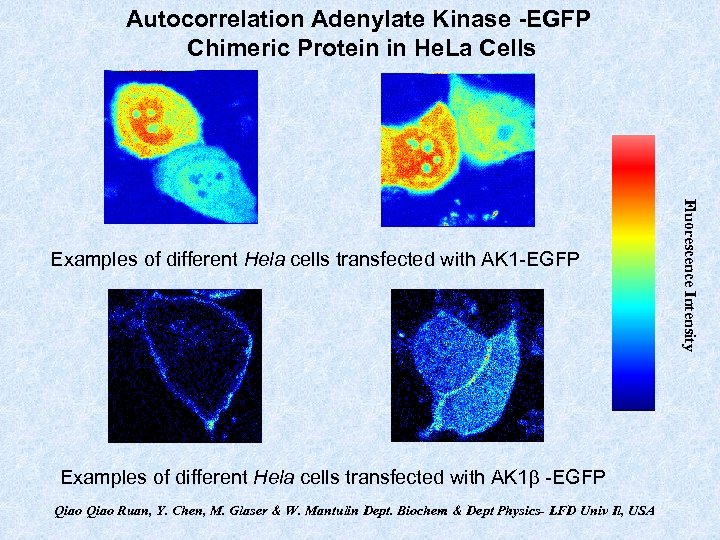Autocorrelation Adenylate Kinase -EGFP Chimeric Protein in He. La Cells Examples of different Hela cells transfected with AK 1 b -EGFP Qiao Ruan, Y. Chen, M. Glaser & W. Mantulin Dept. Biochem & Dept Physics- LFD Univ Il, USA Fluorescence Intensity Examples of different Hela cells transfected with AK 1 -EGFP

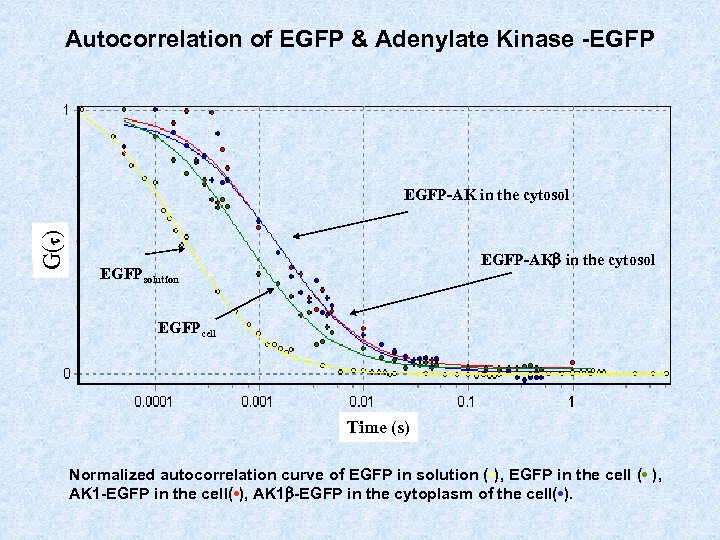Autocorrelation of EGFP & Adenylate Kinase -EGFP G(t) EGFP-AK in the cytosol EGFP-AKb in the cytosol EGFPsolution EGFPcell Time (s) Normalized autocorrelation curve of EGFP in solution ( • ), EGFP in the cell ( • ), AK 1 -EGFP in the cell( • ), AK 1 b-EGFP in the cytoplasm of the cell( • ).

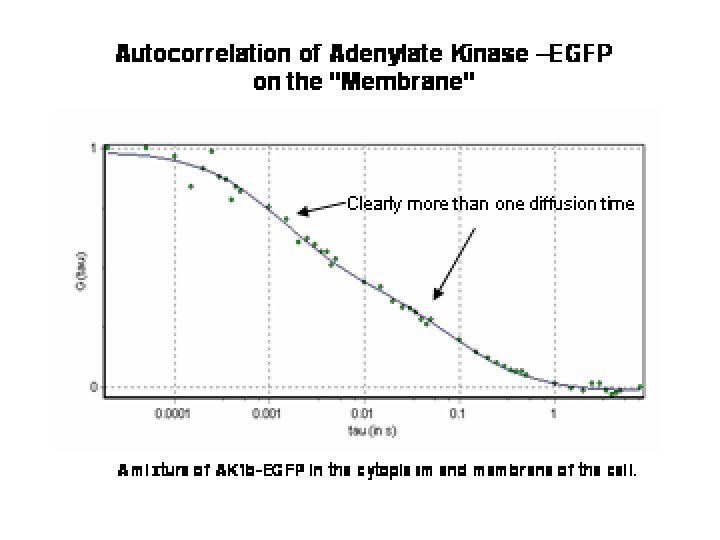
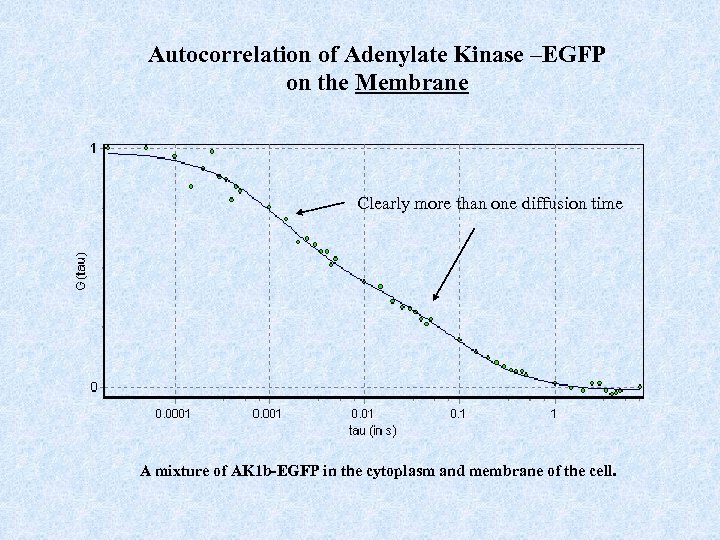Autocorrelation of Adenylate Kinase –EGFP on the Membrane Clearly more than one diffusion time A mixture of AK 1 b-EGFP in the cytoplasm and membrane of the cell.

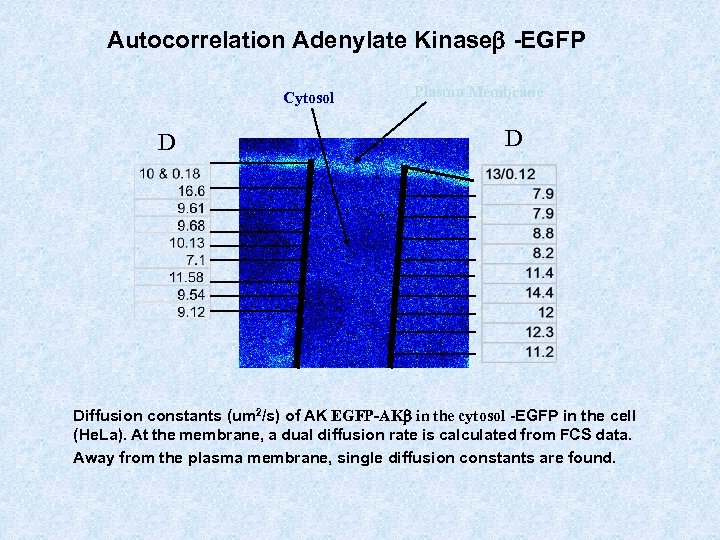Autocorrelation Adenylate Kinaseb -EGFP Cytosol D Plasma Membrane D Diffusion constants (um 2/s) of AK EGFP-AKb in the cytosol -EGFP in the cell (He. La). At the membrane, a dual diffusion rate is calculated from FCS data. Away from the plasma membrane, single diffusion constants are found.

Multiple Species Case 1: Species vary by a difference in diffusion constant, D. Autocorrelation function can be used: (2 D-Gaussian Shape) ! G(0)sample is no longer g/N !

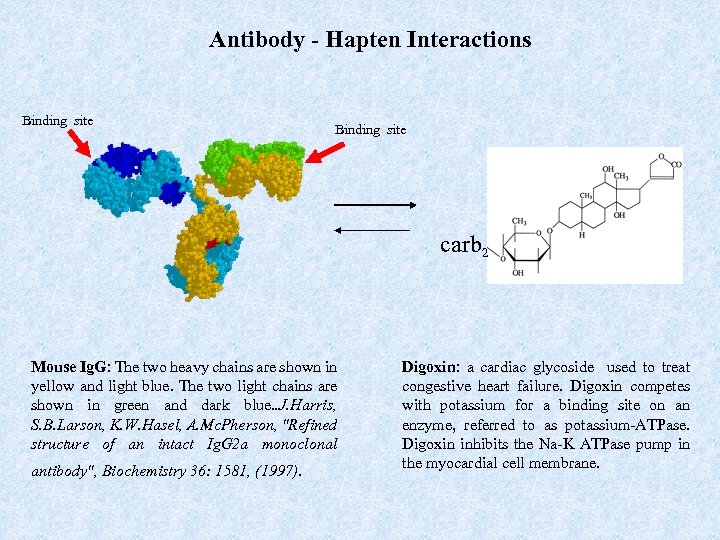Antibody - Hapten Interactions Binding site carb 2 Mouse Ig. G: The two heavy chains are shown in yellow and light blue. The two light chains are shown in green and dark blue. . J. Harris, S. B. Larson, K. W. Hasel, A. Mc. Pherson, "Refined structure of an intact Ig. G 2 a monoclonal antibody", Biochemistry 36: 1581, (1997). Digoxin: a cardiac glycoside used to treat congestive heart failure. Digoxin competes with potassium for a binding site on an enzyme, referred to as potassium-ATPase. Digoxin inhibits the Na-K ATPase pump in the myocardial cell membrane.

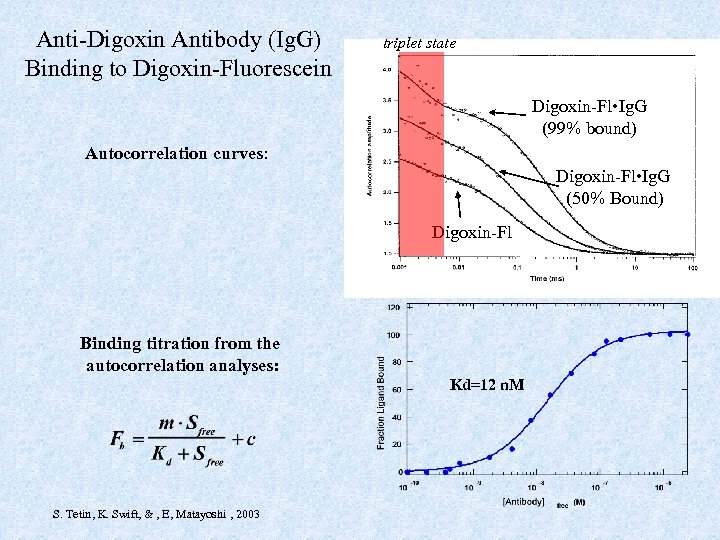Anti-Digoxin Antibody (Ig. G) Binding to Digoxin-Fluorescein triplet state Digoxin-Fl • Ig. G (99% bound) Autocorrelation curves: Digoxin-Fl • Ig. G (50% Bound) Digoxin-Fl Binding titration from the autocorrelation analyses: Kd=12 n. M S. Tetin, K. Swift, & , E, Matayoshi , 2003

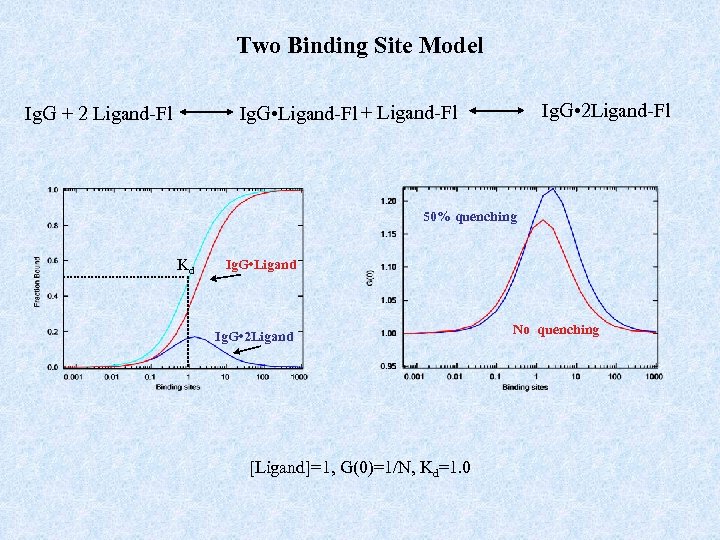Two Binding Site Model Ig. G • 2 Ligand-Fl Ig. G • Ligand-Fl + Ligand-Fl Ig. G + 2 Ligand-Fl 50% quenching Kd Ig. G • Ligand Ig. G • 2 Ligand [Ligand]=1, G(0)=1/N, Kd=1. 0 No quenching

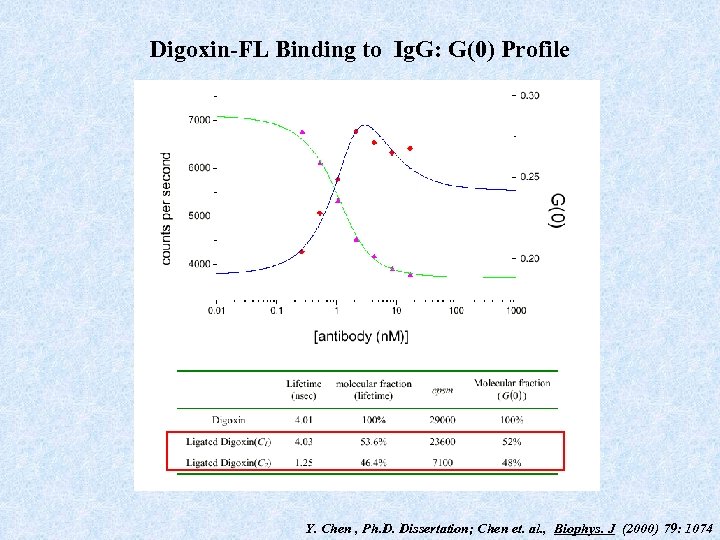Digoxin-FL Binding to Ig. G: G(0) Profile Y. Chen , Ph. D. Dissertation; Chen et. al. , Biophys. J (2000) 79: 1074

Case 2: Species vary by a difference in brightness assuming that The quantity Go becomes the only parameter to distinguish species, but we know that: The autocorrelation function is not suitable for analysis of this kind of data without additional information. We need a different type of analysis

Photon Counting Histogram (PCH) Aim: To resolve species from differences in their molecular brightness Poisson Distribution: Sources of Non-Poissonian Noise Detector Noise Diffusing Particles in an Inhomogeneous Excitation Beam* Particle Number Fluctuations* Multiple Species* Single Species: Where p(k) is the probability of observing k photon counts

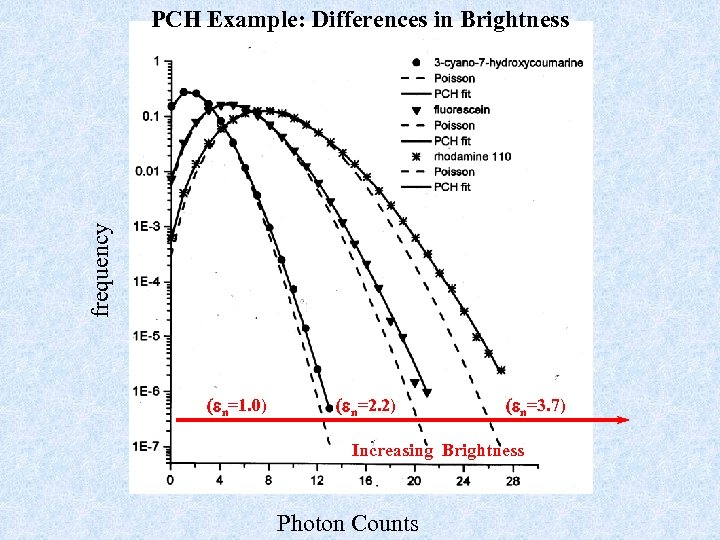frequency PCH Example: Differences in Brightness (en=1. 0) (en=2. 2) (en=3. 7) Increasing Brightness Photon Counts

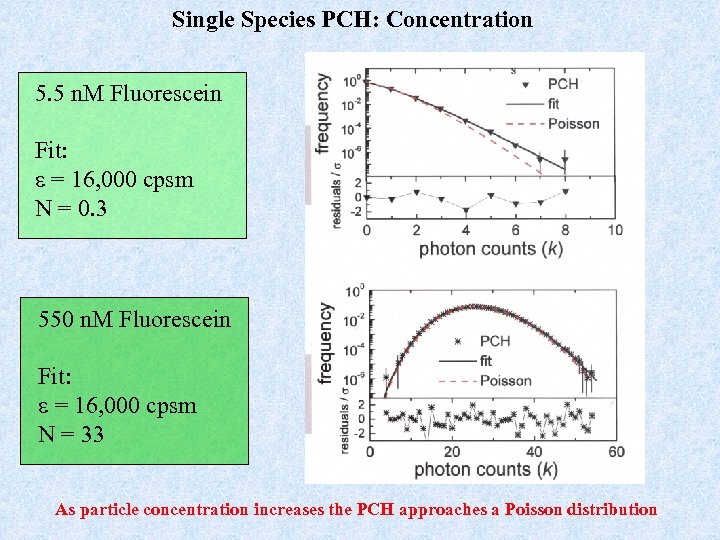Single Species PCH: Concentration 5. 5 n. M Fluorescein Fit: e = 16, 000 cpsm N = 0. 3 550 n. M Fluorescein Fit: e = 16, 000 cpsm N = 33 As particle concentration increases the PCH approaches a Poisson distribution

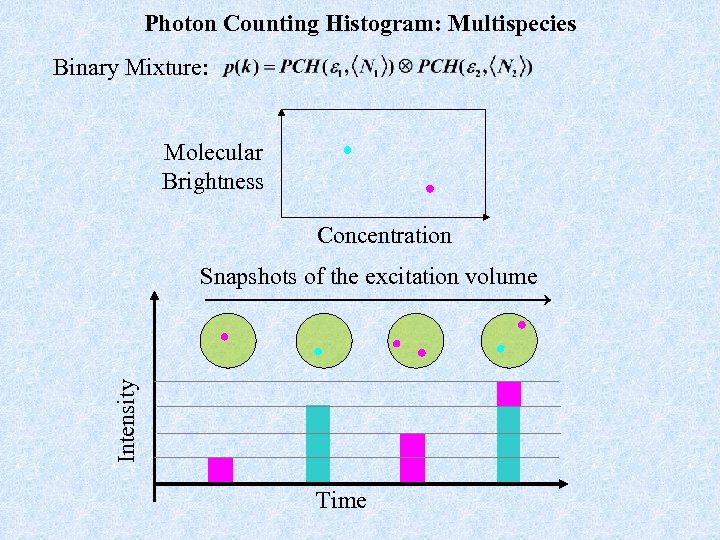Photon Counting Histogram: Multispecies Binary Mixture: Molecular Brightness Concentration Intensity Snapshots of the excitation volume Time

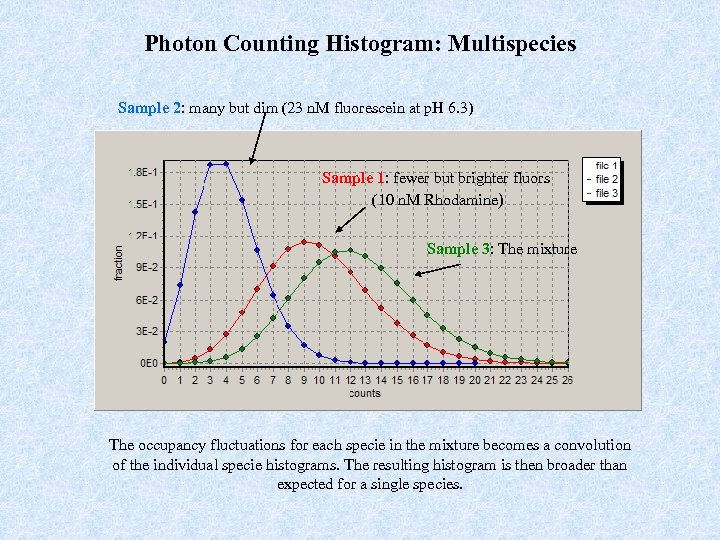Photon Counting Histogram: Multispecies Sample 2: many but dim (23 n. M fluorescein at p. H 6. 3) Sample 1: fewer but brighter fluors (10 n. M Rhodamine) Sample 3: The mixture The occupancy fluctuations for each specie in the mixture becomes a convolution of the individual specie histograms. The resulting histogram is then broader than expected for a single species.

Examination of a Protein Dimer with FCS: Secreted Phospholipase A 2 Sanchez, S. A. , Y. Chen, J. D. Mueller, E. Gratton, T. L. Hazlett. (2001) Biochemistry, 40, 6903 -6911.

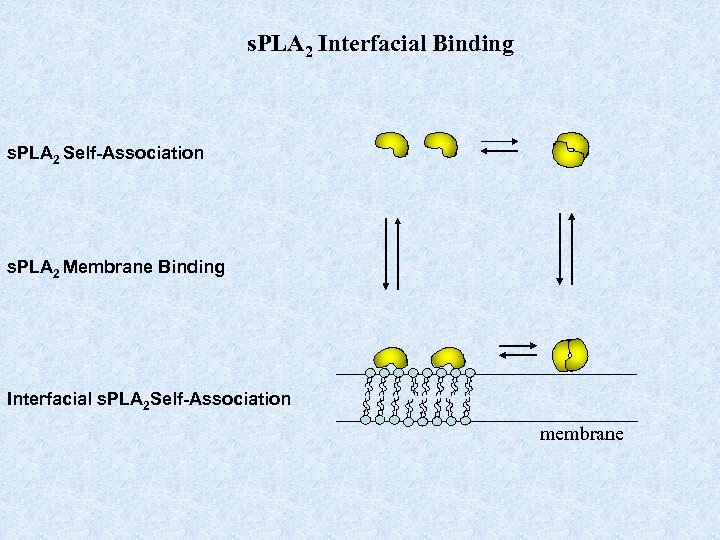s. PLA 2 Interfacial Binding s. PLA 2 Self-Association s. PLA 2 Membrane Binding Interfacial s. PLA 2 Self-Association membrane

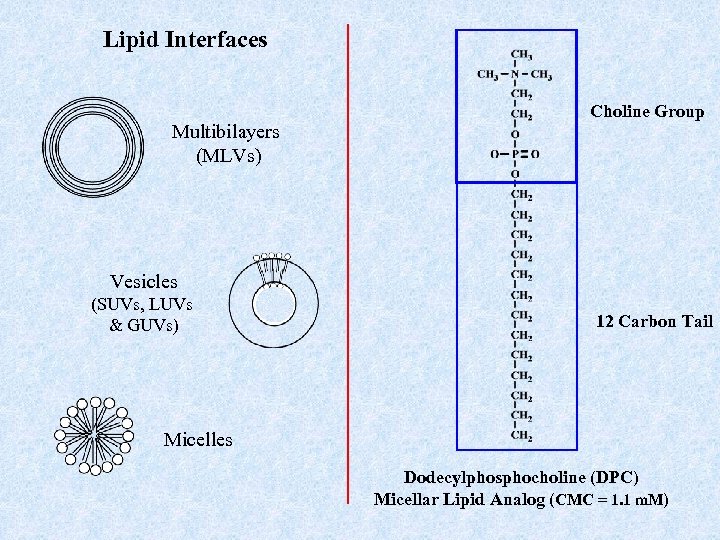Lipid Interfaces Multibilayers (MLVs) Choline Group Vesicles (SUVs, LUVs & GUVs) 12 Carbon Tail Micelles Dodecylphosphocholine (DPC) Micellar Lipid Analog (CMC = 1. 1 m. M)

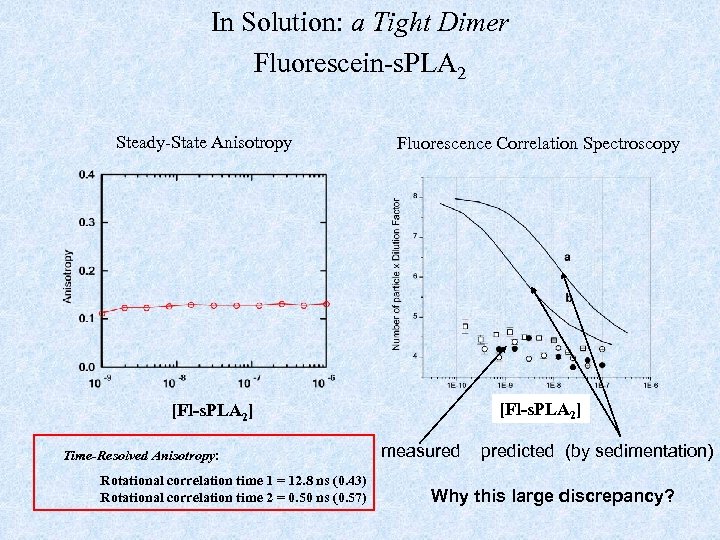In Solution: a Tight Dimer Fluorescein-s. PLA 2 Steady-State Anisotropy Fluorescence Correlation Spectroscopy [Fl-s. PLA 2] Time-Resolved Anisotropy: Rotational correlation time 1 = 12. 8 ns (0. 43) Rotational correlation time 2 = 0. 50 ns (0. 57) measured predicted (by sedimentation) Why this large discrepancy?

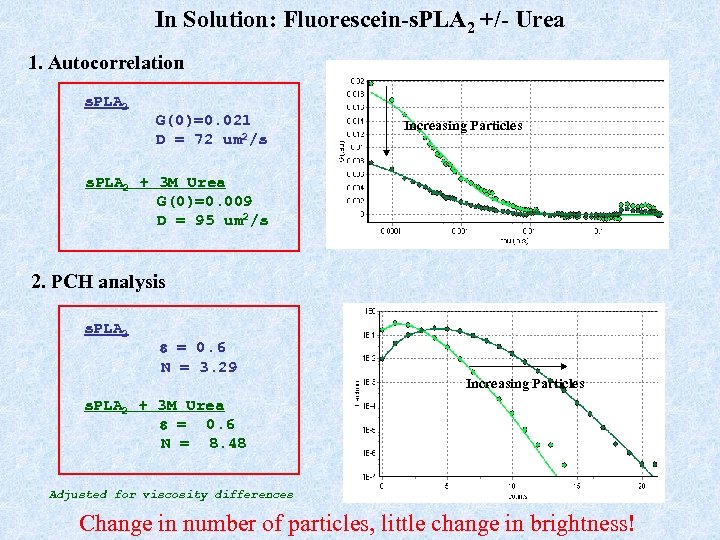In Solution: Fluorescein-s. PLA 2 +/- Urea 1. Autocorrelation s. PLA 2 G(0)=0. 021 D = 72 um 2/s Increasing Particles s. PLA 2 + 3 M Urea G(0)=0. 009 D = 95 um 2/s 2. PCH analysis s. PLA 2 e = 0. 6 N = 3. 29 Increasing Particles s. PLA 2 + 3 M Urea e = 0. 6 N = 8. 48 Adjusted for viscosity differences Change in number of particles, little change in brightness!

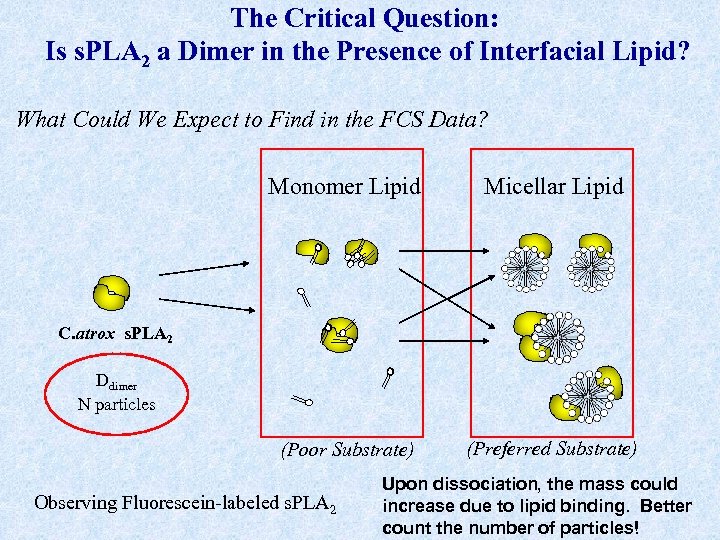The Critical Question: Is s. PLA 2 a Dimer in the Presence of Interfacial Lipid? What Could We Expect to Find in the FCS Data? Monomer Lipid Micellar Lipid (Poor Substrate) (Preferred Substrate) C. atrox s. PLA 2 Ddimer N particles Observing Fluorescein-labeled s. PLA 2 Upon dissociation, the mass could increase due to lipid binding. Better count the number of particles!

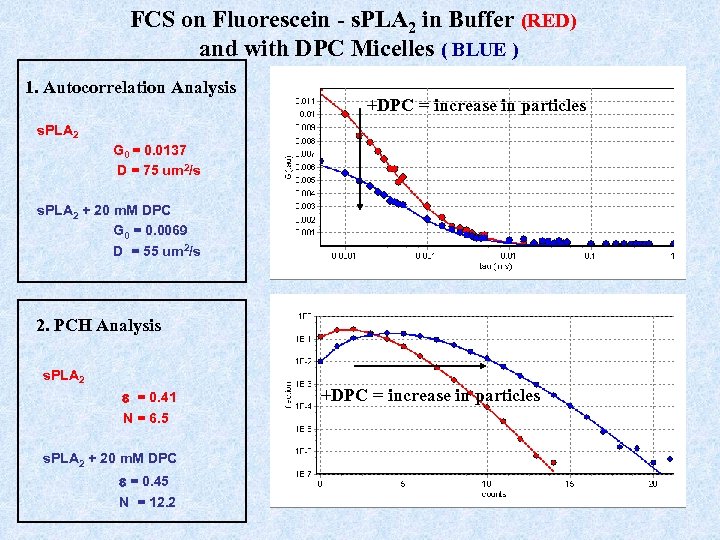FCS on Fluorescein - s. PLA 2 in Buffer (RED) and with DPC Micelles ( BLUE ) 1. Autocorrelation Analysis +DPC = increase in particles s. PLA 2 G 0 = 0. 0137 D = 75 um 2/s s. PLA 2 + 20 m. M DPC G 0 = 0. 0069 D = 55 um 2/s 2. PCH Analysis s. PLA 2 e = 0. 41 N = 6. 5 s. PLA 2 + 20 m. M DPC e = 0. 45 N = 12. 2 +DPC = increase in particles

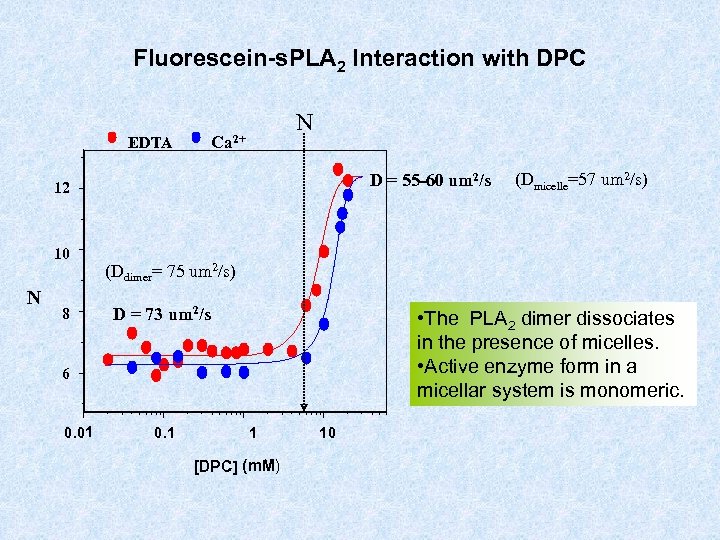Fluorescein-s. PLA 2 Interaction with DPC N Ca 2+ EDTA D = 55 -60 um 2/s 12 10 N 8 (Ddimer= 75 um 2/s) D = 73 um 2/s • The PLA 2 dimer dissociates in the presence of micelles. • Active enzyme form in a micellar system is monomeric. 6 0. 01 (Dmicelle=57 um 2/s) 0. 1 1 [DPC] (m. M) 10

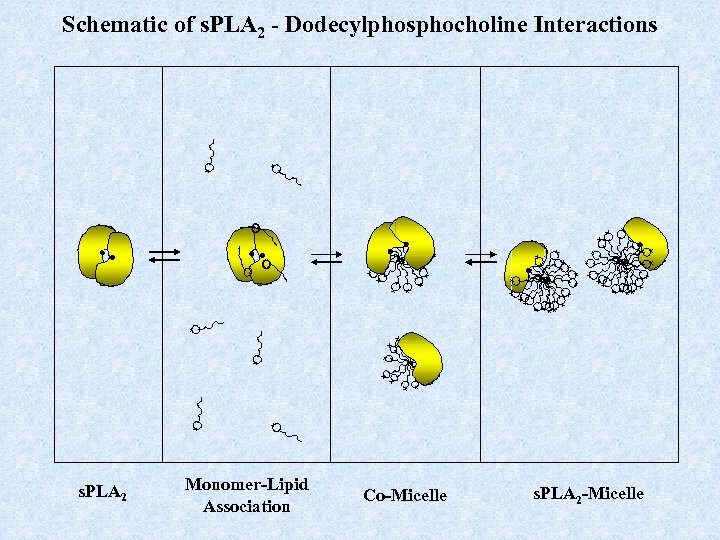Schematic of s. PLA 2 - Dodecylphosphocholine Interactions + + + ++ + + + + + ++ + + + s. PLA 2 + + Monomer-Lipid Association Co-Micelle + + + + + s. PLA 2 -Micelle

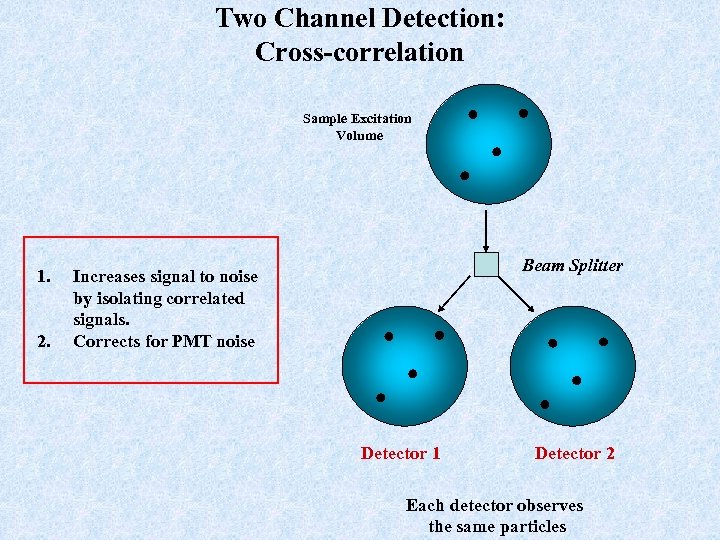Two Channel Detection: Cross-correlation Sample Excitation Volume 1. 2. Beam Splitter Increases signal to noise by isolating correlated signals. Corrects for PMT noise Detector 1 Detector 2 Each detector observes the same particles

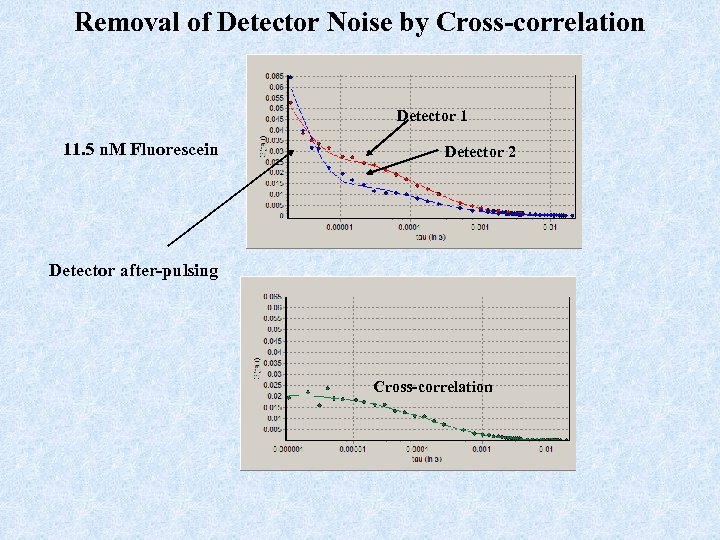Removal of Detector Noise by Cross-correlation Detector 1 11. 5 n. M Fluorescein Detector 2 Detector after-pulsing Cross-correlation

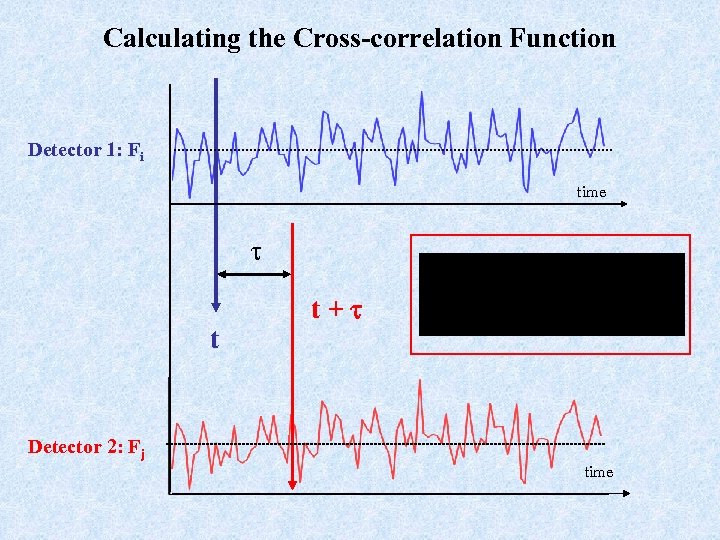Calculating the Cross-correlation Function Detector 1: Fi time t t+t Detector 2: Fj time

Cross-correlation Calculations One uses the same fitting functions you would use for the standard autocorrelation curves. Thus, for a 3 -dimensional Gaussian excitation volume one uses: G 12 is commonly used to denote the cross-correlation and G 1 and G 2 for the autocorrelation of the individual detectors. Sometimes you will see Gx(0) or C(0) used for the cross-correlation.

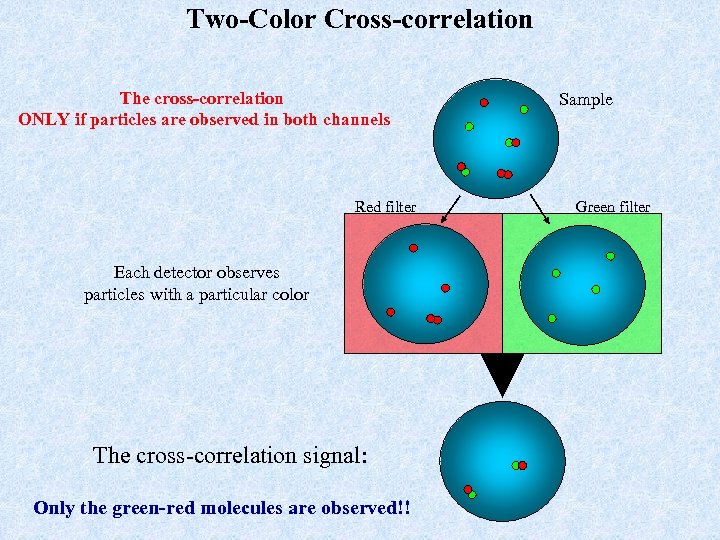Two-Color Cross-correlation The cross-correlation ONLY if particles are observed in both channels Red filter Each detector observes particles with a particular color The cross-correlation signal: Only the green-red molecules are observed!! Sample Green filter

Two-color Cross-correlation Equations are similar to those for the cross correlation using a simple beam splitter: Information Content Correlated signal from particles having both colors. Autocorrelation from channel 1 on the green particles. Autocorrelation from channel 2 on the red particles. Signal

Experimental Concerns: Excitation Focusing & Emission Collection We assume exact match of the observation volumes in our calculations which is difficult to obtain experimentally. Excitation side: (1) Laser alignment (2) Chromatic aberration (3) Spherical aberration Emission side: (1) Chromatic aberrations (2) Spherical aberrations (3) Improper alignment of detectors or pinhole (cropping of the beam and focal point position)

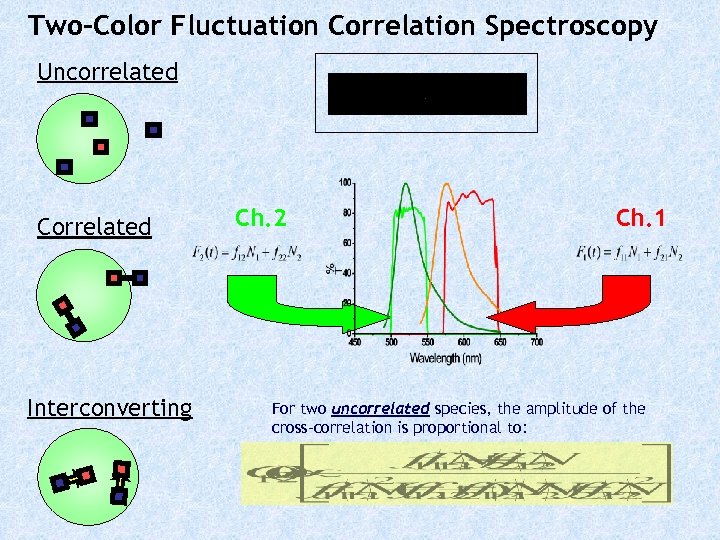Two-Color Fluctuation Correlation Spectroscopy Uncorrelated Correlated Interconverting Ch. 2 Ch. 1 For two uncorrelated species, the amplitude of the cross-correlation is proportional to:

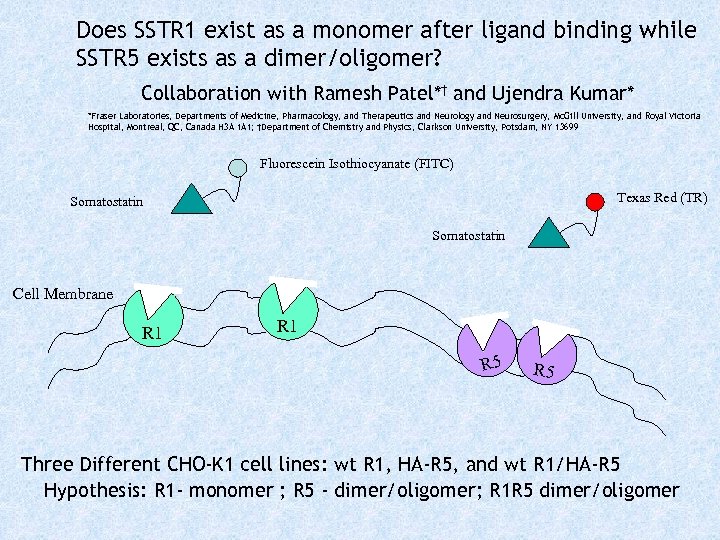Does SSTR 1 exist as a monomer after ligand binding while SSTR 5 exists as a dimer/oligomer? Collaboration with Ramesh Patel*† and Ujendra Kumar* *Fraser Laboratories, Departments of Medicine, Pharmacology, and Therapeutics and Neurology and Neurosurgery, Mc. Gill University, and Royal Victoria Hospital, Montreal, QC, Canada H 3 A 1 A 1; †Department of Chemistry and Physics, Clarkson University, Potsdam, NY 13699 Fluorescein Isothiocyanate (FITC) Texas Red (TR) Somatostatin Cell Membrane R 1 R 5 Three Different CHO-K 1 cell lines: wt R 1, HA-R 5, and wt R 1/HA-R 5 Hypothesis: R 1 - monomer ; R 5 - dimer/oligomer; R 1 R 5 dimer/oligomer

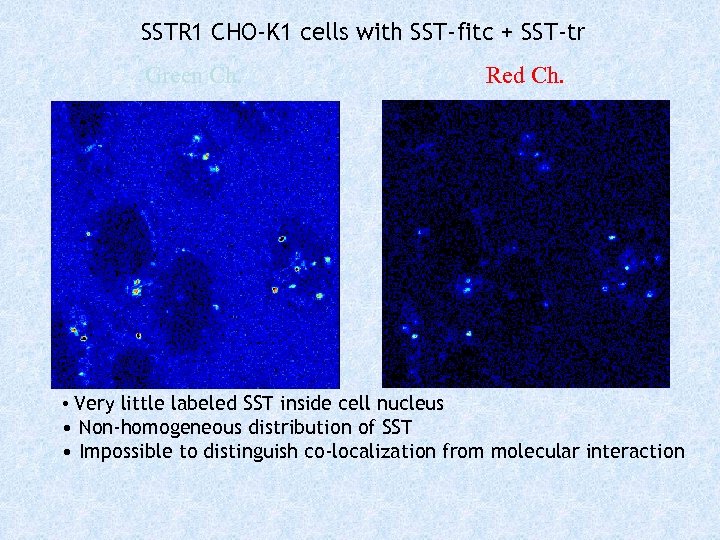SSTR 1 CHO-K 1 cells with SST-fitc + SST-tr Green Ch. Red Ch. • Very little labeled SST inside cell nucleus • Non-homogeneous distribution of SST • Impossible to distinguish co-localization from molecular interaction

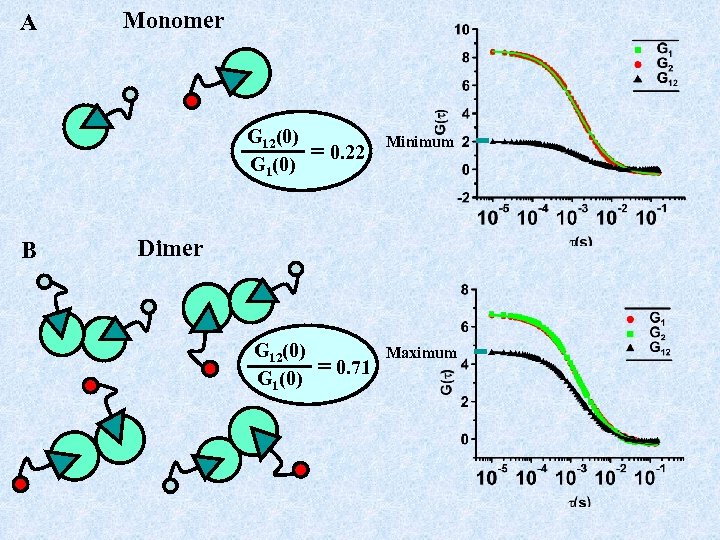A Monomer G 12(0) G 1(0) B = 0. 22 Minimum Dimer G 12(0) G 1(0) = 0. 71 Maximum

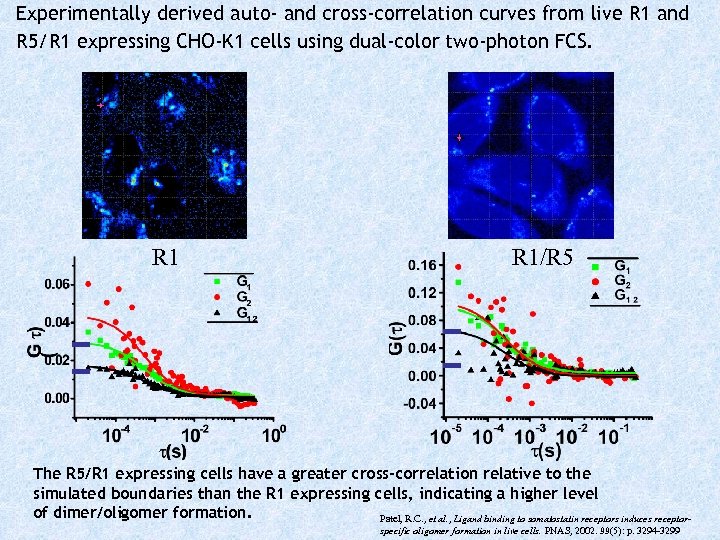Experimentally derived auto- and cross-correlation curves from live R 1 and R 5/R 1 expressing CHO-K 1 cells using dual-color two-photon FCS. R 1/R 5 The R 5/R 1 expressing cells have a greater cross-correlation relative to the simulated boundaries than the R 1 expressing cells, indicating a higher level of dimer/oligomer formation. Patel, R. C. , et al. , Ligand binding to somatostatin receptors induces receptorspecific oligomer formation in live cells. PNAS, 2002. 99(5): p. 3294 -3299

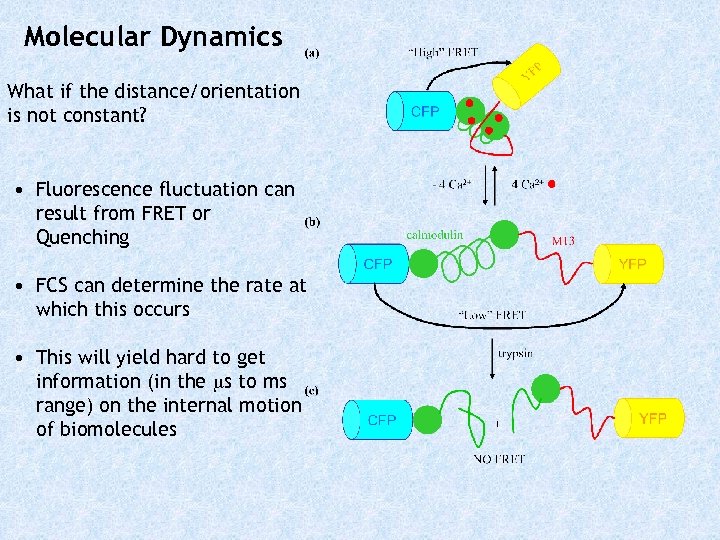Molecular Dynamics What if the distance/orientation is not constant? • Fluorescence fluctuation can result from FRET or Quenching • FCS can determine the rate at which this occurs • This will yield hard to get information (in the s to ms range) on the internal motion of biomolecules

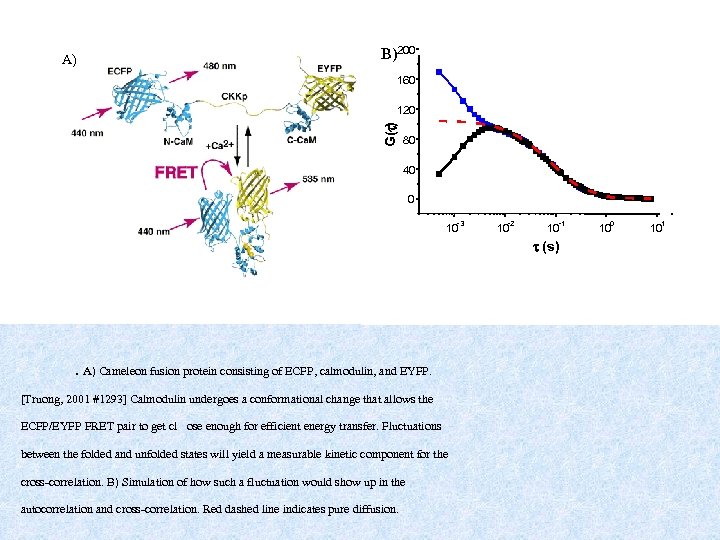A) B)200 160 G(t) 120 80 40 0 -3 10 -2 10 -1 10 t (s) . A) Cameleon fusion protein consisting of ECFP, calmodulin, and EYFP. [Truong, 2001 #1293] Calmodulin undergoes a conformational change that allows the ECFP/EYFP FRET pair to get cl ose enough for efficient energy transfer. Fluctuations between the folded and unfolded states will yield a measurable kinetic component for the cross-correlation. B) Simulation of how such a fluctuation would show up in the autocorrelation and cross-correlation. Red dashed line indicates pure diffusion. 0 10 1 10

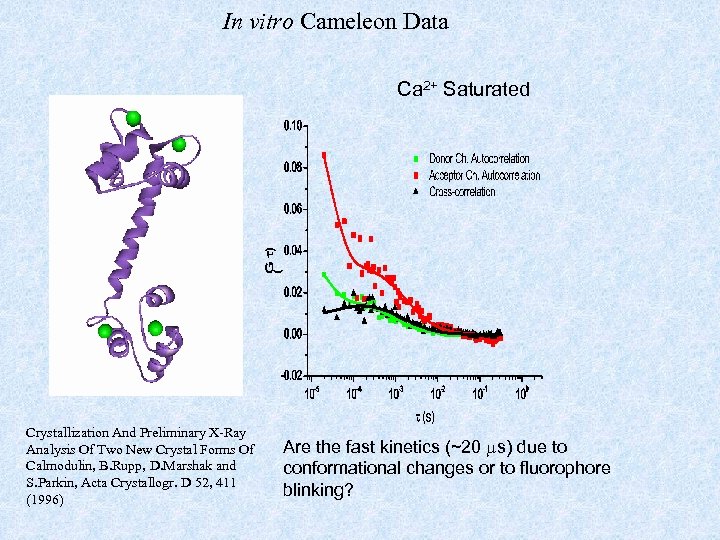In vitro Cameleon Data Ca 2+ Saturated Crystallization And Preliminary X-Ray Analysis Of Two New Crystal Forms Of Calmodulin, B. Rupp, D. Marshak and S. Parkin, Acta Crystallogr. D 52, 411 (1996) Are the fast kinetics (~20 s) due to conformational changes or to fluorophore blinking?

Autocorrelation Adenylate Kinaseb -EGFP Cytosol D Plasma Membrane D Diffusion constants (um 2/s) of AK EGFP-AKb in the cytosol -EGFP in the cell (He. La). At the membrane, a dual diffusion rate is calculated from FCS data. Away from the plasma membrane, single diffusion costants are found.

FRET Efficiency Distribution in Low Mg++ Low-FRET Conformation High-FRET Conformation FRET Efficiency

What is scanning FCS? How is it implemented? What kind of information scanning FCS provides that cannot be obtained with single-point FCS? Definition: “Simultaneous” FCS measurements at multiple sample positions “Simultaneous” = multiplexing Principle: Return to the same location before the particle leaves the volume of observation

Scenarios for Scanning FCS application • Explore spatial-temporal correlation. • Detection and characterization of membrane rafts. Visible raft-like domains “Invisible” raft GUV made from integral membrane fragment How to see the invisible rafts? Probe must be selective for rafts Probe concentration must be large to properly paint the rafts 300 nm Macro scale Nano scale If the rafts are stationary, measurement at only one position will not provide the number of rafts in a pixel If we know the number, we can determine the average size

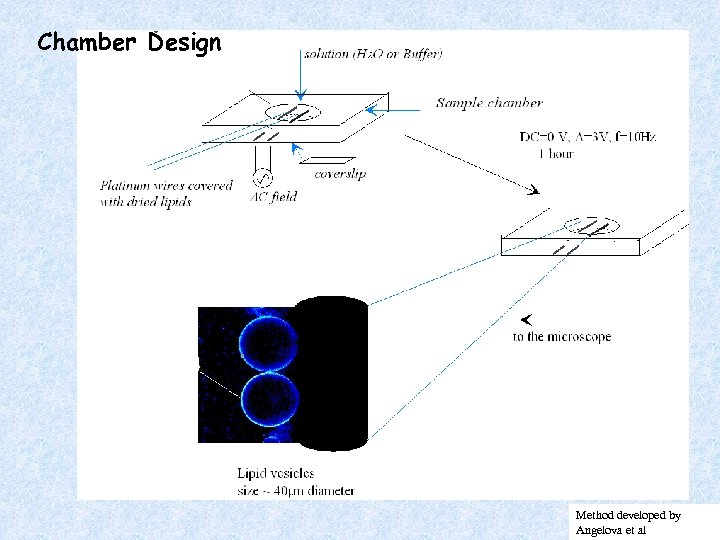Chamber Design Method developed by Angelova et al

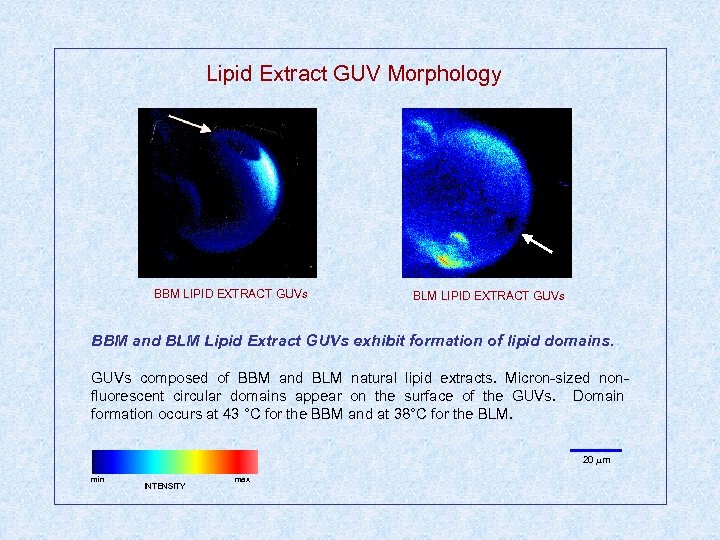Lipid Extract GUV Morphology BBM LIPID EXTRACT GUVs BLM LIPID EXTRACT GUVs BBM and BLM Lipid Extract GUVs exhibit formation of lipid domains. GUVs composed of BBM and BLM natural lipid extracts. Micron-sized nonfluorescent circular domains appear on the surface of the GUVs. Domain formation occurs at 43 °C for the BBM and at 38°C for the BLM. 20 m min INTENSITY max

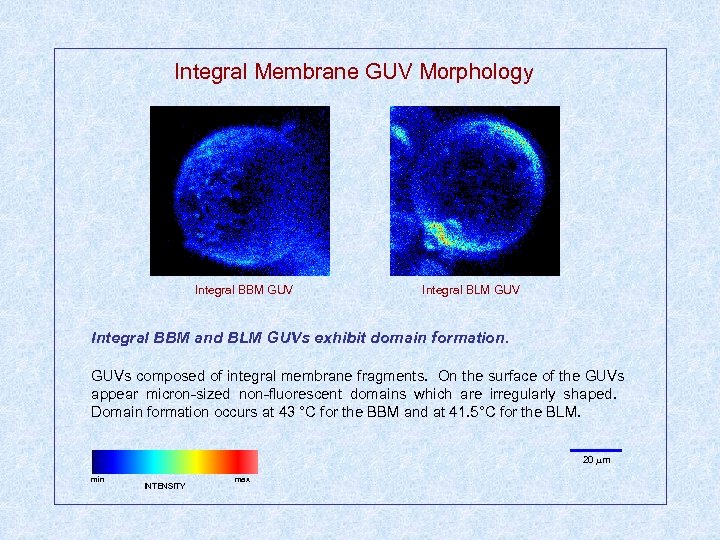Integral Membrane GUV Morphology Integral BBM GUV Integral BLM GUV Integral BBM and BLM GUVs exhibit domain formation. GUVs composed of integral membrane fragments. On the surface of the GUVs appear micron-sized non-fluorescent domains which are irregularly shaped. Domain formation occurs at 43 °C for the BBM and at 41. 5°C for the BLM. 20 m min INTENSITY max

Measure the molecular weight of DNA (Weissman, Proc. Natl. Acad, Sci, USA 73: 2776 (1976)) Measure the Diffusion of Fluorescent Beads and DNA (Koppel and others. Biophysical J. Vol 66: 502, 1994) Advantages: • Improved signal to noise ratio

Data analysis Time Measure association/dissociation equilibrium in protein systems (Berland et al, Biophys. J. 1996)

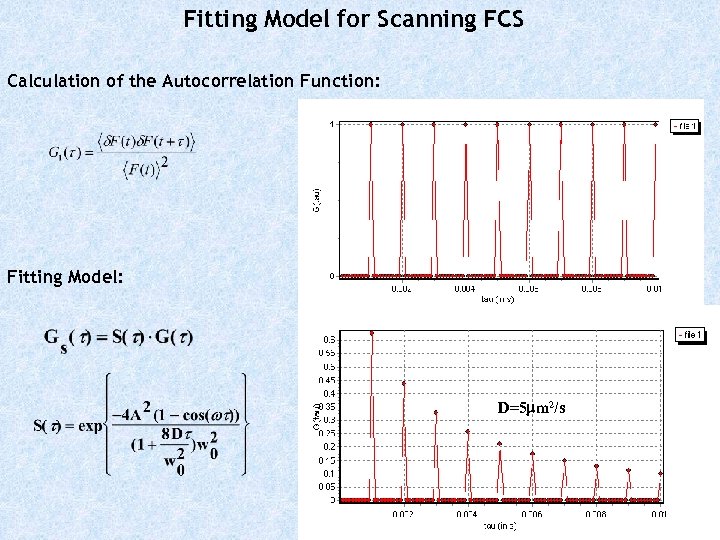Fitting Model for Scanning FCS Calculation of the Autocorrelation Function: Fitting Model: D=5 mm 2/s

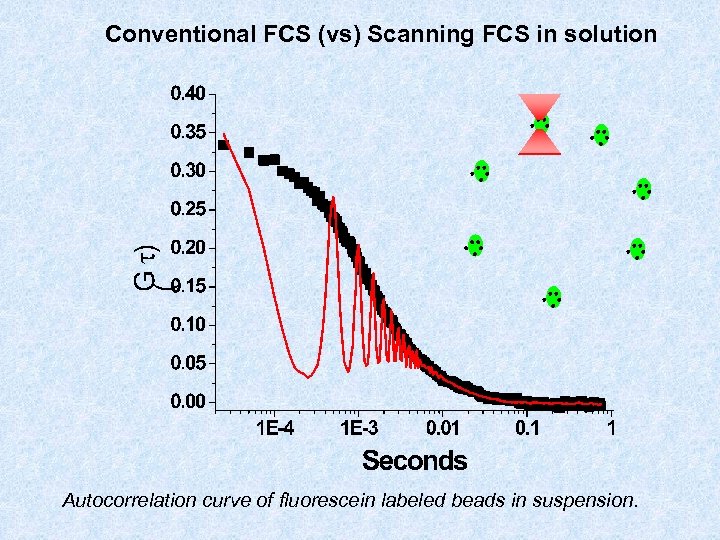Conventional FCS (vs) Scanning FCS in solution Autocorrelation curve of fluorescein labeled beads in suspension.

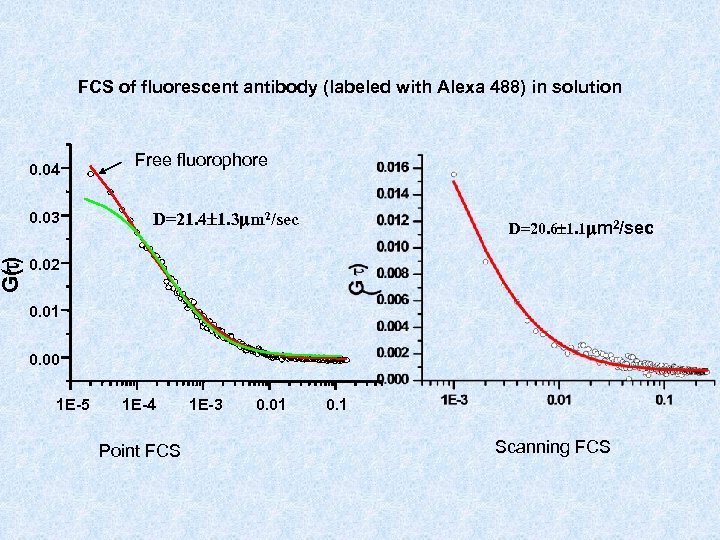G(t) FCS of fluorescent antibody (labeled with Alexa 488) in solution 0. 04 0. 03 Free fluorophore D=21. 4 1. 3 mm 2/sec D=20. 6 1. 1 mm 2/sec 0. 02 0. 01 0. 00 1 E-5 1 E-4 Point FCS 1 E-3 0. 01 0. 1 Scanning FCS

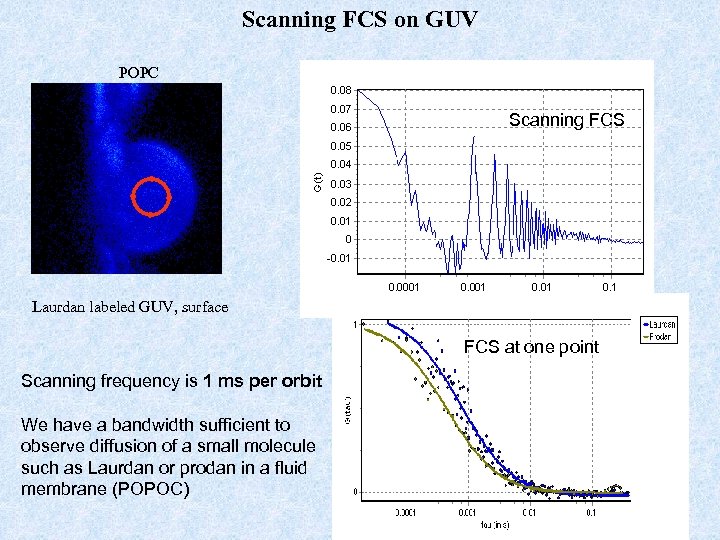Scanning FCS on GUV POPC Scanning FCS Laurdan labeled GUV, surface FCS at one point Scanning frequency is 1 ms per orbit We have a bandwidth sufficient to observe diffusion of a small molecule such as Laurdan or prodan in a fluid membrane (POPOC)

Advantage of scanning FCS for membrane and cellular studies • • • Less photo damage Easy to locate membrane border Multiple points simultaneously Distinguish moving from immobile fraction Spatial cross correlation… Velocity direction and gradients

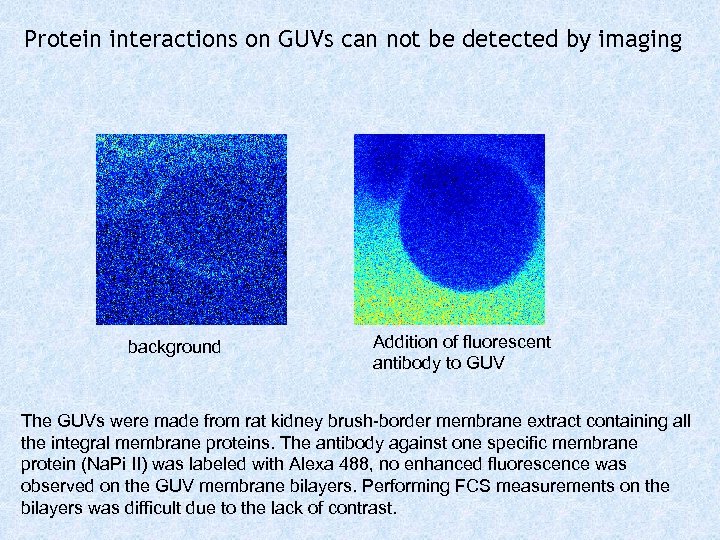Protein interactions on GUVs can not be detected by imaging background Addition of fluorescent antibody to GUV The GUVs were made from rat kidney brush-border membrane extract containing all the integral membrane proteins. The antibody against one specific membrane protein (Na. Pi II) was labeled with Alexa 488, no enhanced fluorescence was observed on the GUV membrane bilayers. Performing FCS measurements on the bilayers was difficult due to the lack of contrast.

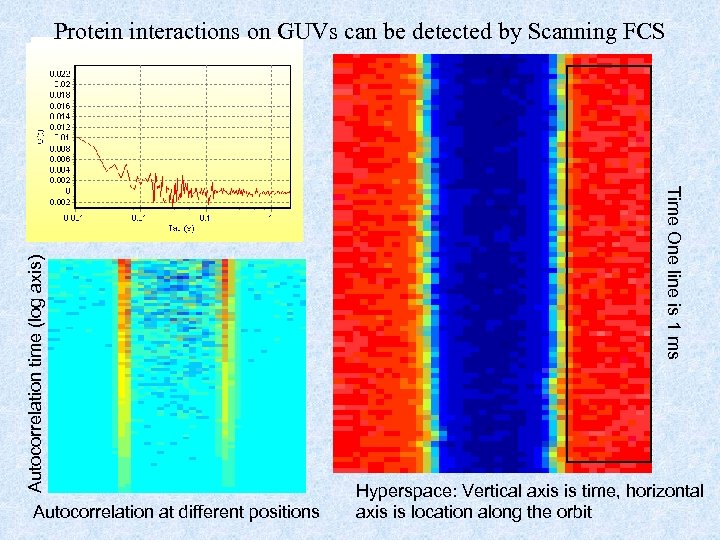Autocorrelation at different positions Time One line is 1 ms Autocorrelation time (log axis) Protein interactions on GUVs can be detected by Scanning FCS Hyperspace: Vertical axis is time, horizontal axis is location along the orbit

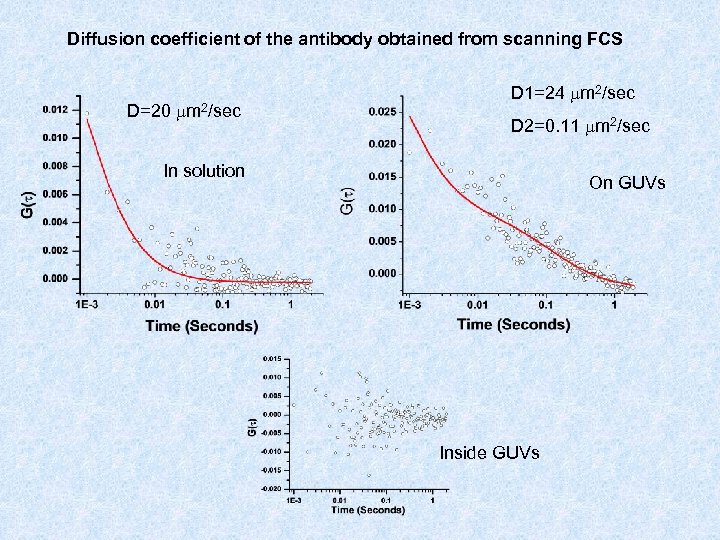Diffusion coefficient of the antibody obtained from scanning FCS D=20 m 2/sec D 1=24 m 2/sec D 2=0. 11 m 2/sec In solution On GUVs Inside GUVs

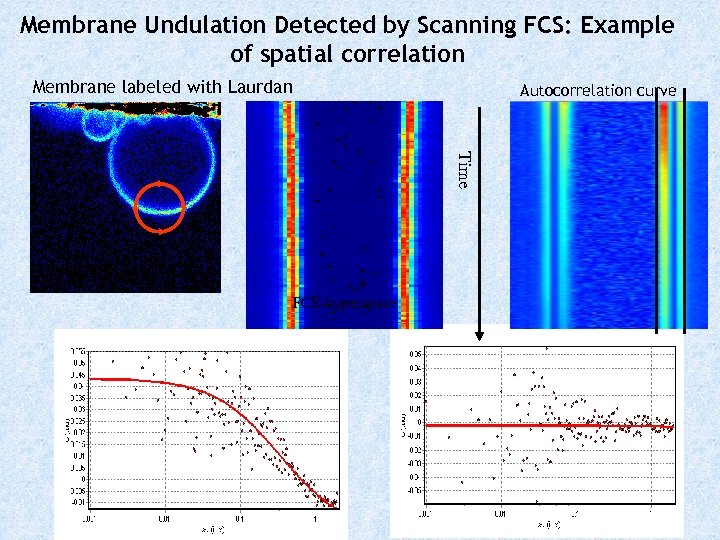Membrane Undulation Detected by Scanning FCS: Example of spatial correlation Membrane labeled with Laurdan Autocorrelation curve Time Mid section of GUV FCS-hyperspace

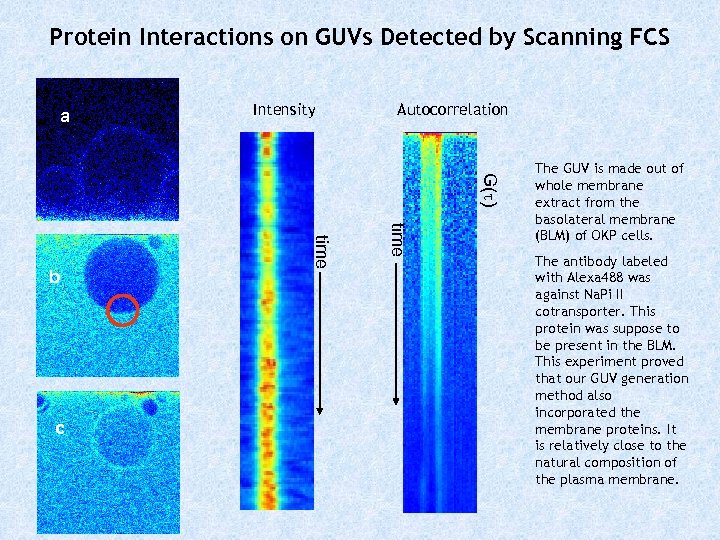Protein Interactions on GUVs Detected by Scanning FCS a Intensity Autocorrelation G( ) time c time b The GUV is made out of whole membrane extract from the basolateral membrane (BLM) of OKP cells. The antibody labeled with Alexa 488 was against Na. Pi II cotransporter. This protein was suppose to be present in the BLM. This experiment proved that our GUV generation method also incorporated the membrane proteins. It is relatively close to the natural composition of the plasma membrane.

Conclusions Scanning FCS is feasible both in solution, in model membranes and in cells When the characteristic times for diffusion (or reactions) are about 1 ms or longer, it could be convenient to perform scanning FCS Scanning FCS provides autocorrelation functions at many positions in the sample in a multiplexing way Scanning FCS offers the possibility to distinguish processes such as true diffusion and flow from local movements Scanning FCS allows to clearly distinguish the location (and movements) of membranes proteins and membrane domain while performing FCS measurements Scanning FCS can be used to determine with nanometer precision the positions of particles (molecules) and membranes