Lecture 4 Multiplier using FPGA 2007 09 28 Prof C

Lecture 4 Multiplier using FPGA 2007/09/28 Prof. C. M. Kyung

Multiplier using FPGA 1. GOAL is (1) How to design more complex combinational circuit, multiplier, using HDL(Hardware Description Language) for a wide range of logic system. (2) How to analyze and implement the two basic combinational multiplier forms-“array multiplier” and “parallel multiplier”. (3) In particular, how to represent the multiplier through sequential circuit instead of combinational circuit. 2/13

Multiplier using FPGA 2. Multiplication (1) Multiplication for binary numbers 0 x 0 = 0, 0 x 1 = 0, 1 x 0 = 0, 1 x 1=1 (2) Shifting & adding operation (partial product & sum of product) 3/13

Multiplier using FPGA 3. Multiplier (1) Array multiplier (2) Parallel multiplier (3) Sequential multiplier 4/13

Multiplier using FPGA 3. Multiplier (1) Array multiplier - Partial product generation and accumulation are merged 5/13

Multiplier using FPGA 3. Multiplier (1) Array multiplier - Partial product generation and accumulation are merged - Classic shift-add multiplication Adder structure used to combine all the bit products in a multiplier Logical bit products AND of the bits from each input Basic structure is simple to implement in FPGAs Not make efficient use of the logic in many FPGAs Larger and slower than other implementations - Ripple carry array multiplier (also called row ripple form) - Carry save array multiplier 6/13

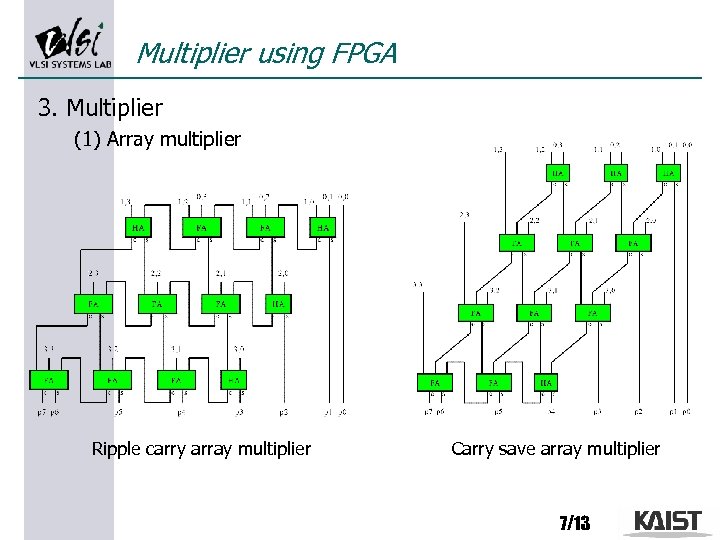Multiplier using FPGA 3. Multiplier (1) Array multiplier Ripple carry array multiplier Carry save array multiplier 7/13

Multiplier using FPGA (2) Parallel multiplier - High-speed multiplication partial products Array Multiplier multiplicand multiplier Adder tree Adder array result - Reduce the number of partial products. - Speed up the multiplication. - The gain in speed is obtained at the expense of extra hardware. - Parallel multiplier can be implemented so as to support a high rate of pipelining. 8/13

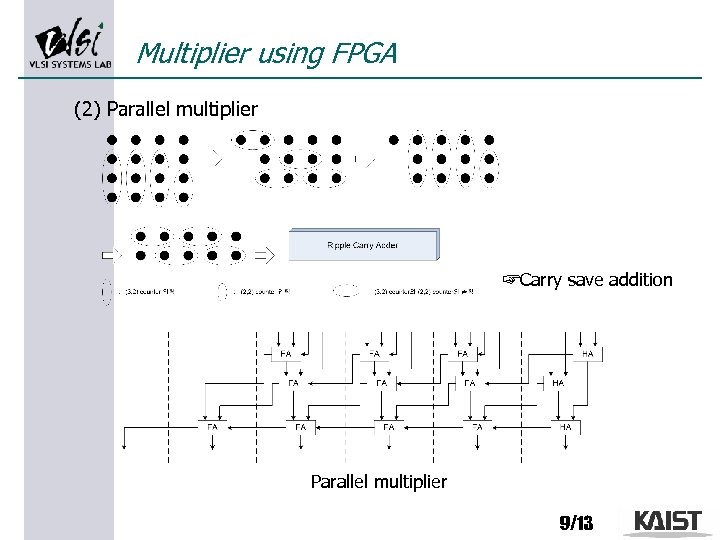Multiplier using FPGA (2) Parallel multiplier ☞Carry save addition Parallel multiplier 9/13

Multiplier using FPGA (3) Sequential multiplier - U = XA - Representation of X : signed-magnitude : 2’s complement : 1’ complement - If X is positive, P(j+1) = (P(j) + xj A) 2 -1; j = 0, 1, . . . , n-2, P(0) = 0 U = 2 n-1 P(n-1) accumulated partial products 10/13

Multiplier using FPGA 3. Problem statement (1) Design m*n (unsigned) array multiplier (2) Design k*k (unsigned) parallel multiplier (3) Design k*k (unsigned) sequential multiplier (4) For each multiplier(1~3), Verilog coding & simulation 11/13

Multiplier using FPGA 4. Experiment Requirements (1) Verilog (2) Quartus II 12/13

Multiplier using FPGA 5. References & Contact (1) Textbook - Randy H. Katz, Contemporary Logic Design, (1994) - Charles H. Roth Jr. , Fundamentals of Logic Design, (2004) - Israel Koren, Computer Arithmetic Algorithms, (2002) (2) 4 th Week T. A. E-mail bs_choi@kaist. ac. kr arashi@odyssey. kaist. ac. kr (Ext. 8032) (3) Lecture Homepage http: //wink. kaist. ac. kr/course/ee 306/ 13/13