Lecture 4 Allometry and Scaling with examples of

Lecture 4: Allometry and Scaling with examples of correlation and regression 1

Allometry = "different measure" = the study of how and why properties of organisms change in regular ways in relation to body size. Scaling = essentially a synonymous term in biology, but used more in engineering. Can be studied at three levels: 1. ontogenetic (intraspecific) = growth relationships during development, between two traits or between one trait and the whole organism: a. longitudinal = follow individuals b. cross-sectional = mixed-age sample 2

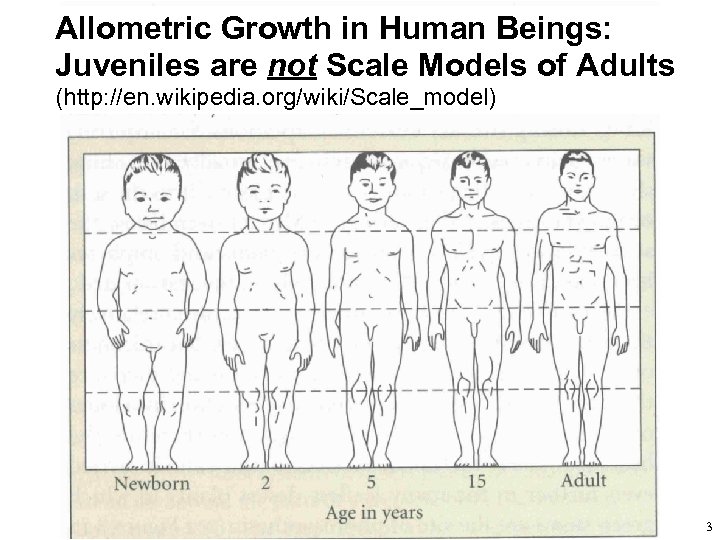Allometric Growth in Human Beings: Juveniles are not Scale Models of Adults (http: //en. wikipedia. org/wiki/Scale_model) 3

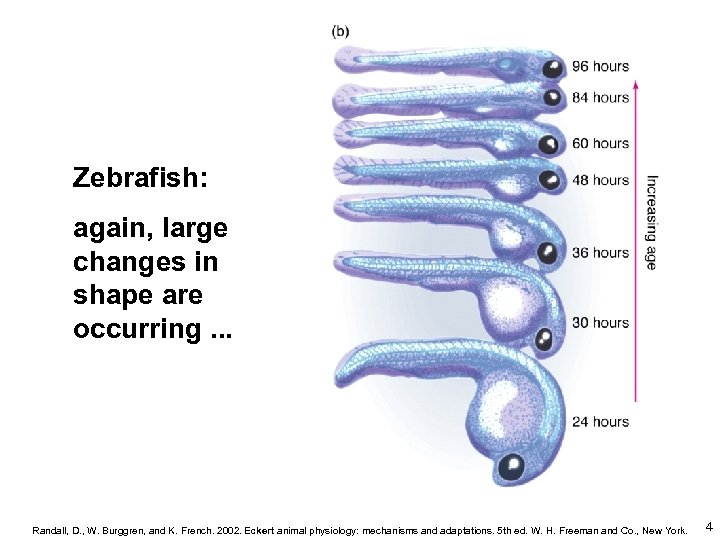Zebrafish: again, large changes in shape are occurring. . . Randall, D. , W. Burggren, and K. French. 2002. Eckert animal physiology: mechanisms and adaptations. 5 th ed. W. H. Freeman and Co. , New York. 4

Allometric growth is differential rates of growth of two or more traits. It is often well described by the equation: Y = b. X a where Y is one trait (e. g. , metabolic rate), b is a constant, a is the "allometric" or "scaling" coefficient, and X is the other trait (often a measure of body size, e. g. , mass or length). 5

Y = b. X a This equation describes a logarithmic relationship. It can be made linear by taking the logs of the values measured for each trait, or by plotting on log-log graph paper. If we take logs, then the equation becomes: log Y = log b + a log X This equation describes a straight line with a being the slope. 6

"Reptiles" (not a good term, phylogenetically speaking) are a good model for studies of ontogenetic allometry because: 1. they have little or no parental care, so newly hatched or born offspring must fend for themselves, forage, escape from predators, etc. ; 2. huge size range from juvenile to adult; 3. no metamorphosis to complicate the picture. 7

An Example of Studying Ontogenetic Allometry: Amphibolurus (Ctenophorus) nuchalis from central Australian National Bird Recent Hatchling Adult Male Adult Female 8

Fowler’s Gap: a Research Station and Working Sheep Ranch run by the University of New South Wales 9

Fowler’s Gap: a Research Station and Working Sheep Ranch run by the University of New South Wales 10

Area around Fowler’s Gap: Lizards often Bask on Fence Posts, or use them for Territorial Outposts 11

Fences can be Hazardous to Emu and Kangaroo! 12

The Wet Season can be Hazardous to Vehicles! 13

Lizard Burrows can be in Surprising Places 14

Amphibolurus (Ctenophorus) nuchalis Convergent Evolution with North American Dipsosaurus dorsalis (desert iguana) 15

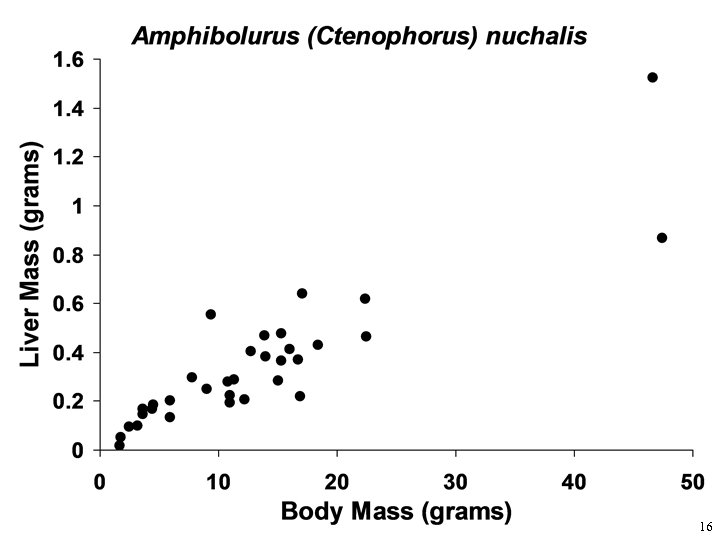16

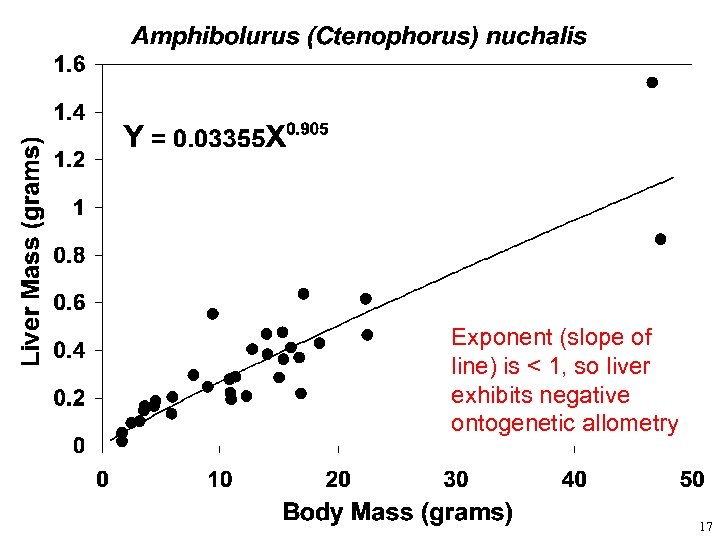Exponent (slope of line) is < 1, so liver exhibits negative ontogenetic allometry 17

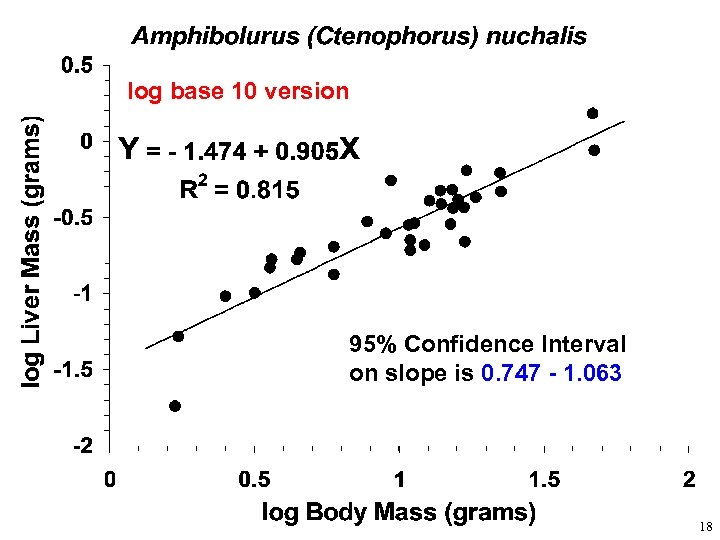log base 10 version 95% Confidence Interval on slope is 0. 747 - 1. 063 18

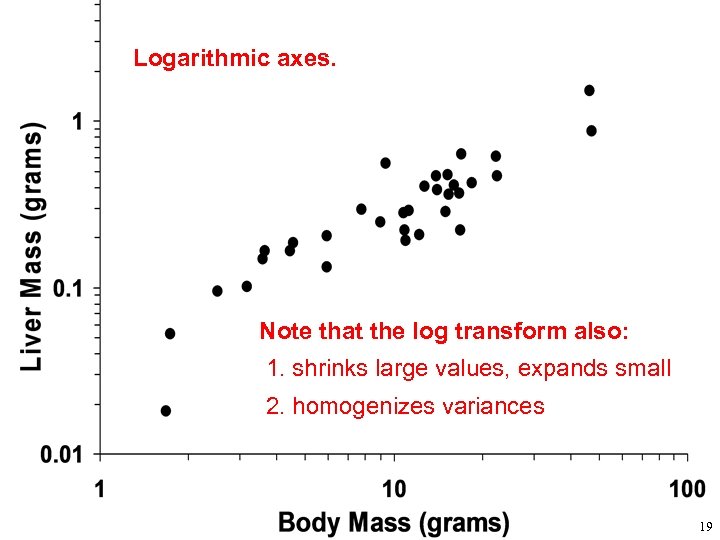Logarithmic axes. Note that the log transform also: 1. shrinks large values, expands small 2. homogenizes variances 19

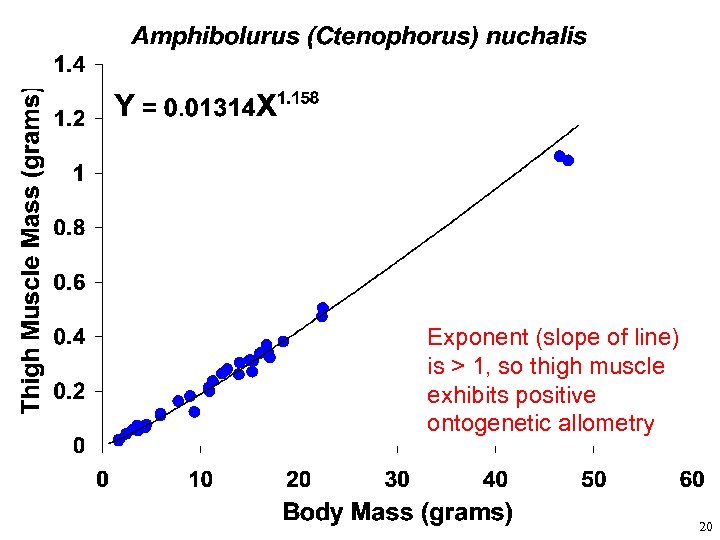Exponent (slope of line) is > 1, so thigh muscle exhibits positive ontogenetic allometry 20

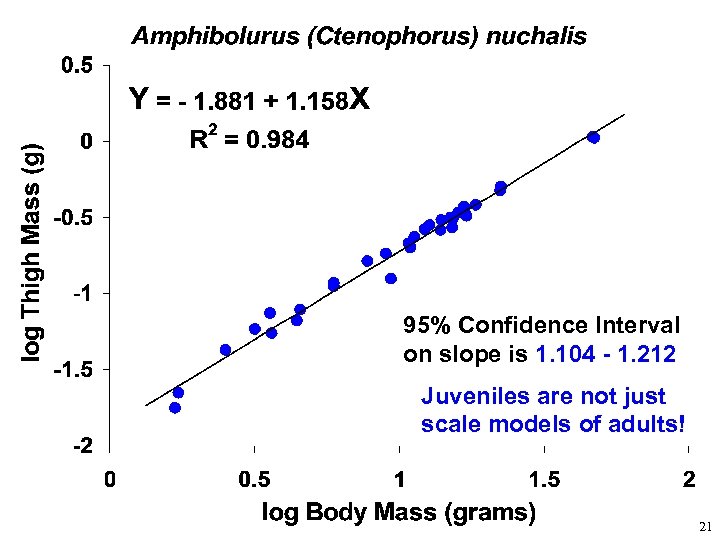95% Confidence Interval on slope is 1. 104 - 1. 212 Juveniles are not just scale models of adults! 21

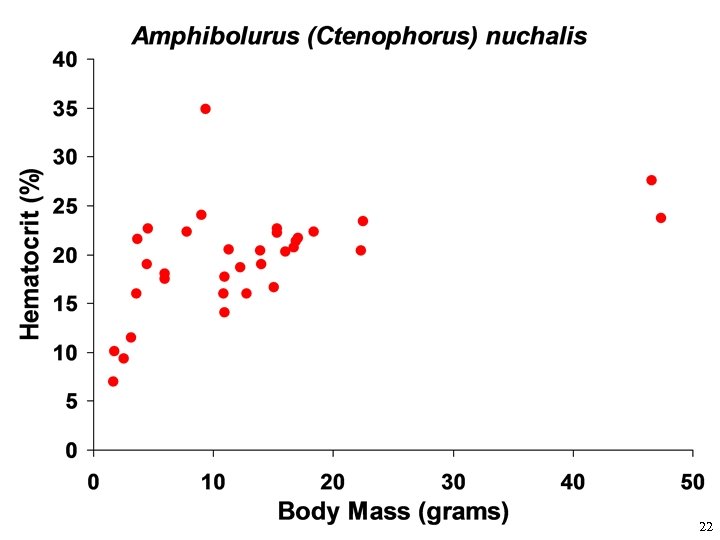22

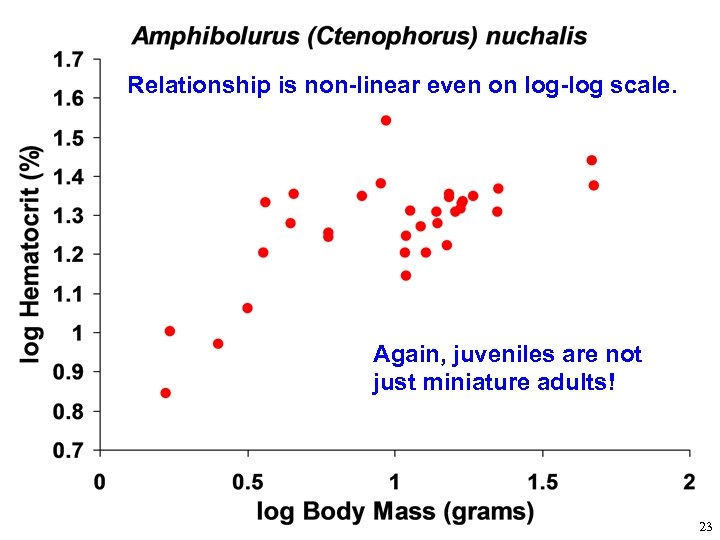Relationship is non-linear even on log-log scale. Again, juveniles are not just miniature adults! 23

Non-linear ontogenetic allometries (on log-log scale) of physiological traits also occur in garter snakes and water snakes, and in many amphibians around metamorphosis. The common garter snake, Thamnophis sirtalis 24

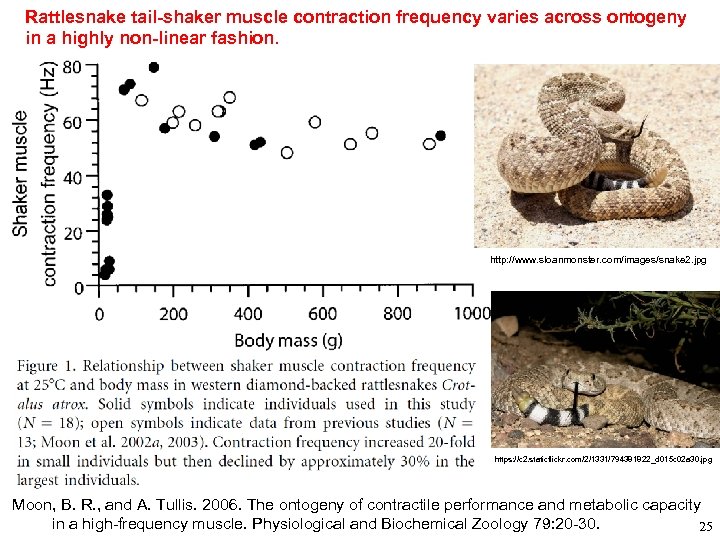Rattlesnake tail-shaker muscle contraction frequency varies across ontogeny in a highly non-linear fashion. http: //www. sloanmonster. com/images/snake 2. jpg https: //c 2. staticflickr. com/2/1331/794381822_d 015 c 02 a 30. jpg Moon, B. R. , and A. Tullis. 2006. The ontogeny of contractile performance and metabolic capacity in a high-frequency muscle. Physiological and Biochemical Zoology 79: 20 -30. 25

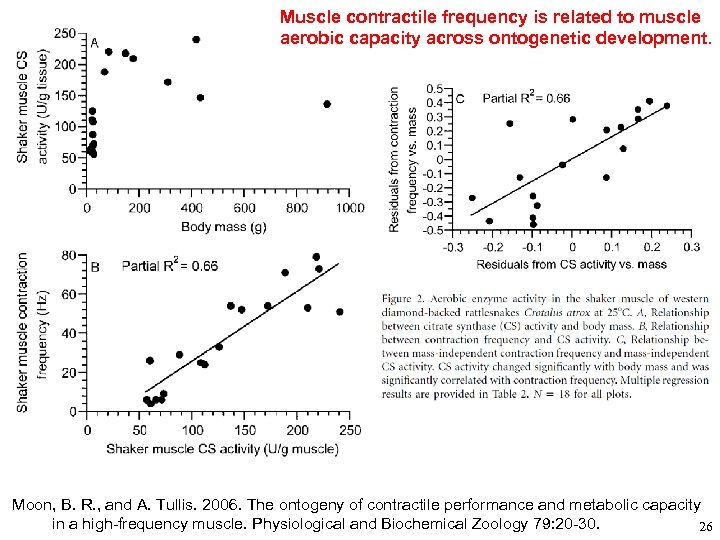Muscle contractile frequency is related to muscle aerobic capacity across ontogenetic development. Moon, B. R. , and A. Tullis. 2006. The ontogeny of contractile performance and metabolic capacity in a high-frequency muscle. Physiological and Biochemical Zoology 79: 20 -30. 26

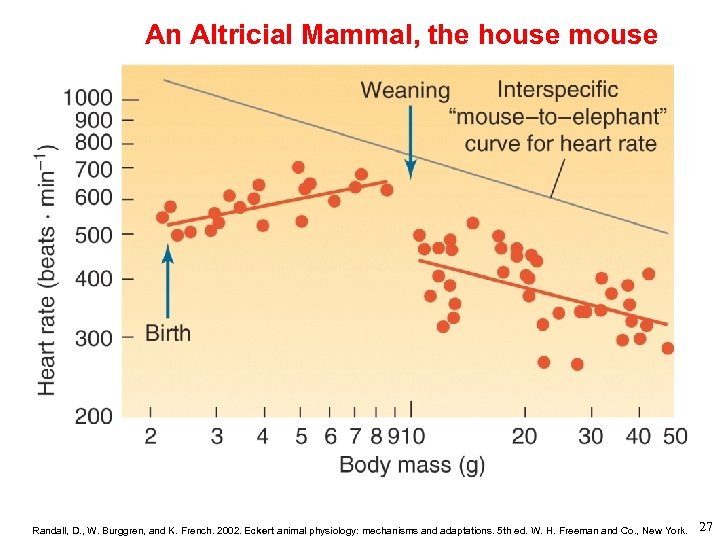An Altricial Mammal, the house mouse Randall, D. , W. Burggren, and K. French. 2002. Eckert animal physiology: mechanisms and adaptations. 5 th ed. W. H. Freeman and Co. , New York. 27

Some Differences between Hatchling and Adult Amphibolurus (Ctenophorus) nuchalis: Ratio 50/1 1 g 50 g Liver, % body mass 3. 4 2. 3 0. 69 Heart, % body mass 0. 27 0. 40 1. 51 Thigh, % body mass 1. 31 2. 44 1. 86 Hindlimb span/SVL 1. 52 1. 25 0. 82 Hematocrit (%) 6. 0 20. 7 3. 44 How might these differences affect organismal performance? Stopped here 13 Jan. 2015 28

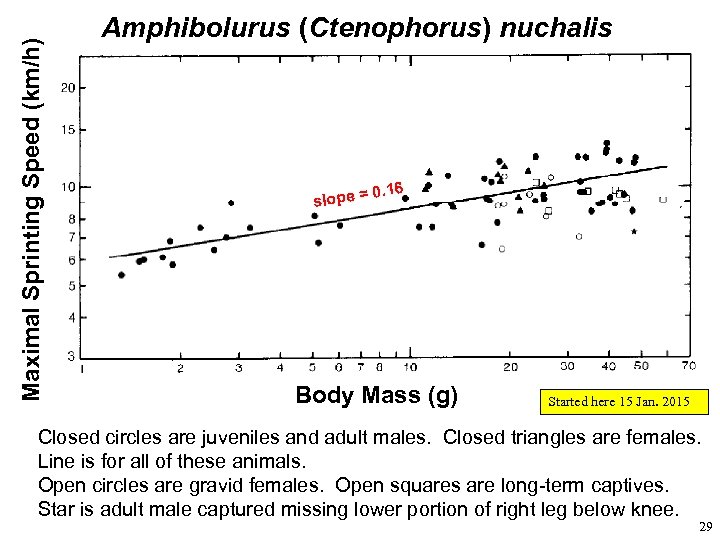Maximal Sprinting Speed (km/h) Amphibolurus (Ctenophorus) nuchalis . 16 0 slope = Body Mass (g) Started here 15 Jan. 2015 Closed circles are juveniles and adult males. Closed triangles are females. Line is for all of these animals. Open circles are gravid females. Open squares are long-term captives. Star is adult male captured missing lower portion of right leg below knee. 29

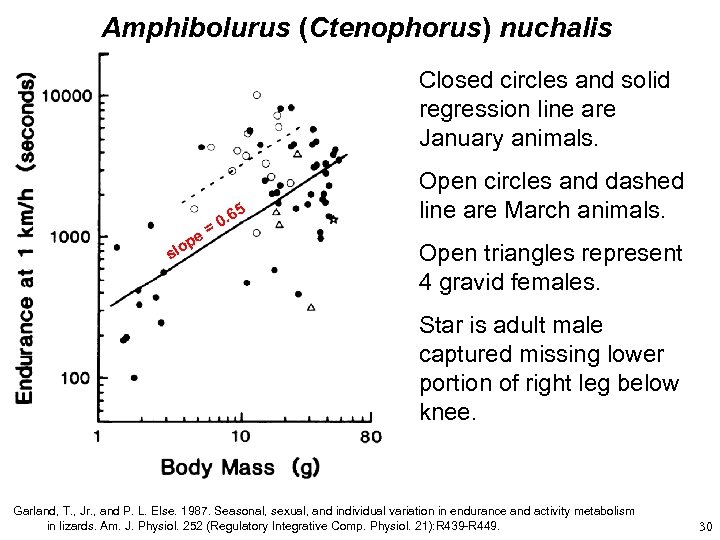Amphibolurus (Ctenophorus) nuchalis Closed circles and solid regression line are January animals. 5 e lop s . 6 =0 Open circles and dashed line are March animals. Open triangles represent 4 gravid females. Star is adult male captured missing lower portion of right leg below knee. Garland, T. , Jr. , and P. L. Else. 1987. Seasonal, sexual, and individual variation in endurance and activity metabolism in lizards. Am. J. Physiol. 252 (Regulatory Integrative Comp. Physiol. 21): R 439 -R 449. 30

Take-home Messages for the Lizard Ontogenetic Allometry Example: 1. Juveniles are not "scale models" of adults; they are not just miniature adults. 2. They differ in both shape and physiological functions. 3. The scaling of locomotor performance (speed, stamina) could not have been predicted simply from the scaling of the lower-level traits presented (e. g. , muscle mass, hematocrit). 4. However, development of mechanistic models may allow us to get there in the future … 31

Additional levels at which allometry can be studied: 2. static = size relationships of traits among individuals of the same age (typically adults) 3. evolutionary (interspecific) = size relationships among species This is a perennial favorite of comparative and ecological physiologists! It pervades the fields. Many books have been written. 32

Books on Allometry (mainly interspecific): Brown, J. H. , and G. B. West, eds. 2000. Scaling in biology. Oxford Univ. Press, New York. Calder, W. A. 1984. Size, function and life history. Harvard Univ. Press, Cambridge. Peters, R. H. 1983. The ecological implications of body size. Cambridge Univ. Press, Cambridge. Reiss, M. J. 1989. The allometry of growth and reproduction. Cambridge Univ. Press, Cambridge. Schmidt-Nielsen, K. 1984. Scaling: why is animal size so important? Cambridge Univ. Press, Cambridge. (You do not need to remember all of these, but note that you have a reading from the last one. ) 33

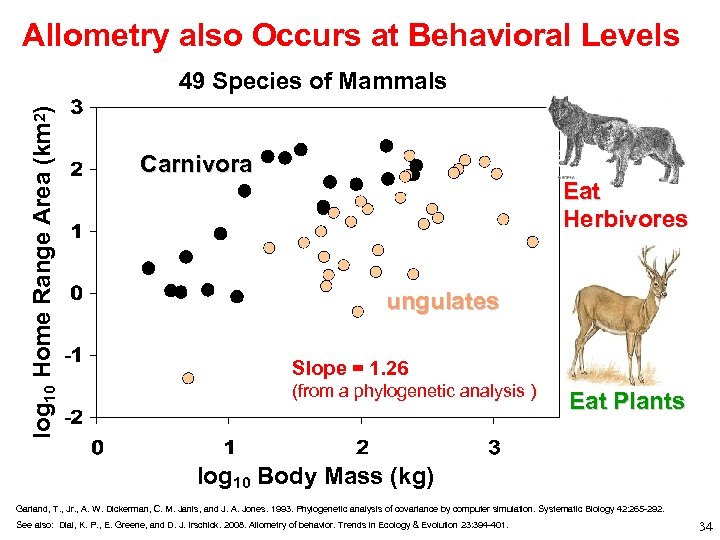Allometry also Occurs at Behavioral Levels log 10 Home Range Area (km 2) 49 Species of Mammals Carnivora Eat Herbivores ungulates Slope = 1. 26 (from a phylogenetic analysis ) Eat Plants log 10 Body Mass (kg) Garland, T. , Jr. , A. W. Dickerman, C. M. Janis, and J. A. Jones. 1993. Phylogenetic analysis of covariance by computer simulation. Systematic Biology 42: 265 -292. See also: Dial, K. P. , E. Greene, and D. J. Irschick. 2008. Allometry of behavior. Trends in Ecology & Evolution 23: 394 -401. 34

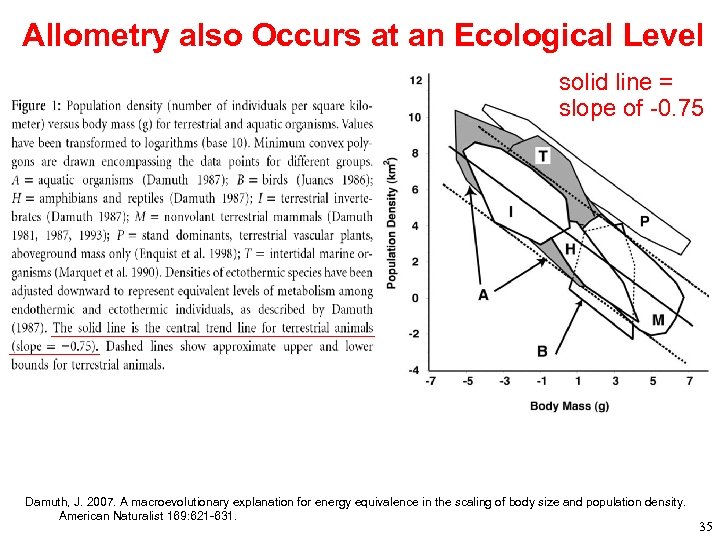Allometry also Occurs at an Ecological Level solid line = slope of -0. 75 Damuth, J. 2007. A macroevolutionary explanation for energy equivalence in the scaling of body size and population density. American Naturalist 169: 621 -631. 35

Allometry: Predictions from First Principles; A Tool to Understand Organismal Design and Adaptation 36

Scaling Relationships Based on First Principles For geometrically similar objects (scale models): Relationships with Length Circumference Length 1 1 (for a circle, circumference 2 * π * radius ) 2 Cross-sectional Area Length (for a circle, area π * radius 2) Surface Area Length 2 Volume Length 3 3 (for a sphere, volume 4/3 π * radius ) 3 Mass Length (assuming that density remains constant) 37

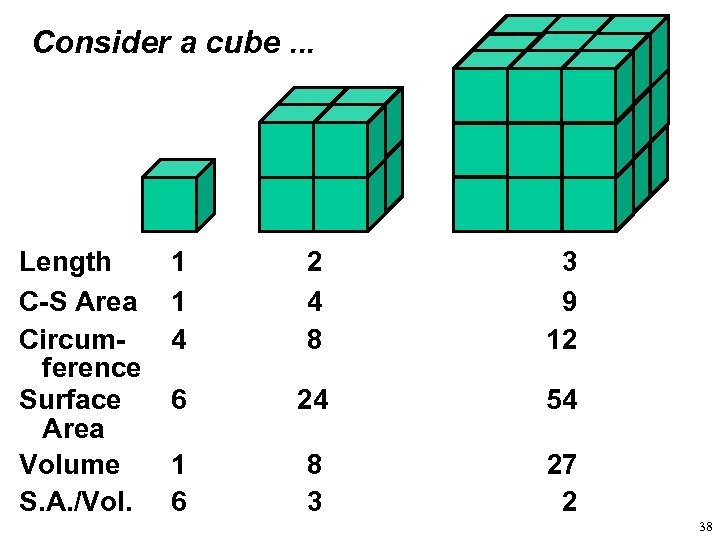Consider a cube. . . Length C-S Area Circumference Surface Area Volume S. A. /Vol. 1 1 4 2 4 8 3 9 12 6 24 54 1 6 8 3 27 2 38

Relationships with Mass Volume is proportional to Mass 1. 00 Length is proportional to Mass 0. 33 Surface Area is proportional to Mass 0. 67 Predictions for geometrically similar animals: Blood Volume is proportional to Mass 1. 00 Mass of Organ is proportional to Body Mass 1. 00 Limb Length is proportional to Body Mass 0. 33 Skin, Gill or Lung Surface Area Mass 0. 67 39

Allometric Expectations Based on First Principles for Geometrically Similar Objects (scale models) serve as Null Models for Comparison with Real Organisms. Deviations from "isometry" may indicate how evolution has modified organisms from geometric similarity in order to maintain (more or less) functional abilities across a range of body sizes. (Only may indicate because this presumes that evolutionary changes in size because of random genetic drift, in the absence of selection, would occur along lines of geometric similarity …) 40

Example: Mammalian Skeletal Mass As body mass becomes larger, would need bone strength to keep up. Strength cross-sectional area, so would need bone cross-sectional area M 1. 00 to support the load. Mass of skeleton would be M 1. 00 X M 0. 33 = M 1. 33 needed c-s area X length Empirical result: skeletal mass M 1. 08+0. 04 So, large mammals should not be able to do what small ones do (unless all are "over-designed"). In fact, large mammals have more upright postures, less dynamic & less risky locomotor behavior (elephants don’t jump). 41

Example: Metabolic Rate Amount of (metabolically active) tissue should dictate the rate at which an animal produces heat (or consumes oxygen). Oxygen consumption at rest or during maximum exertion should be M 1. 00 However, respiratory exchange surface area should be M 0. 67 "Houston, we have a problem …" 42

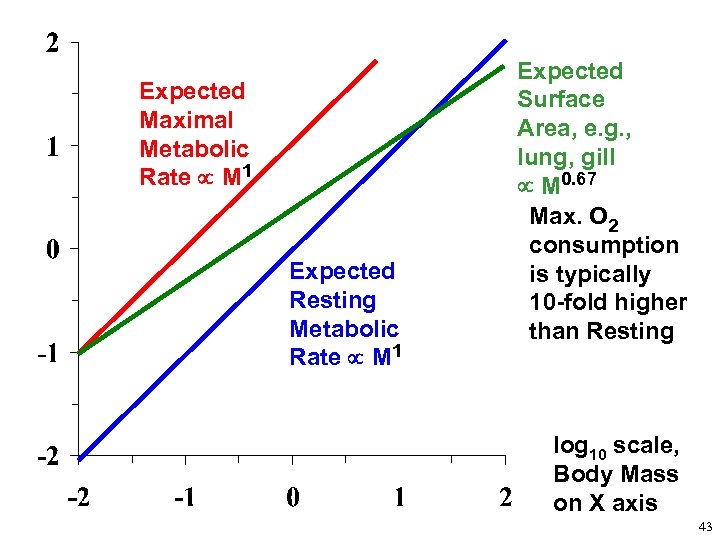Expected Maximal Metabolic Rate M 1 Expected Resting Metabolic Rate M 1 Expected Surface Area, e. g. , lung, gill M 0. 67 Max. O 2 consumption is typically 10 -fold higher than Resting log 10 scale, Body Mass on X axis 43

What gives? Metabolic rate typically scales with an exponent less than unity, often ~ 0. 7 -0. 8 (many exceptions). 44

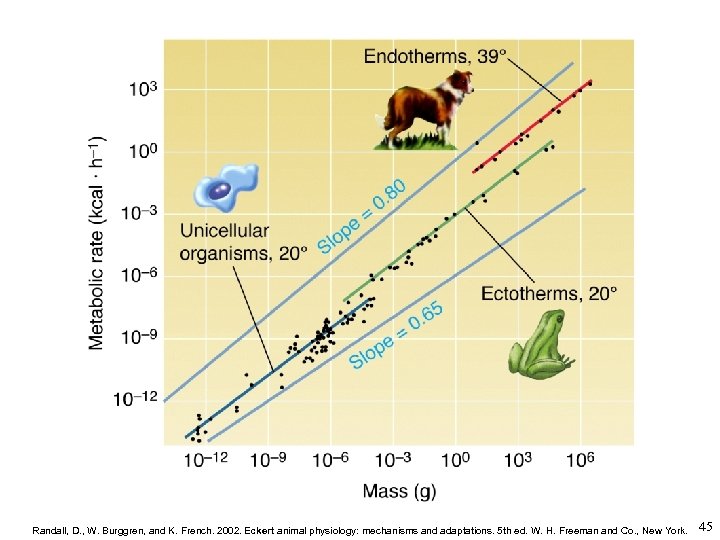Randall, D. , W. Burggren, and K. French. 2002. Eckert animal physiology: mechanisms and adaptations. 5 th ed. W. H. Freeman and Co. , New York. 45

What gives? Metabolic rate typically scales with an exponent less than unity, often ~ 0. 7 -0. 8 (many exceptions). Gas exchange surface area often scales with an exponent greater than 0. 67. But, the slopes do not always match. Example: mammalian maximal oxygen consumption (measured on motorized treadmill) scales as M 0. 872 46

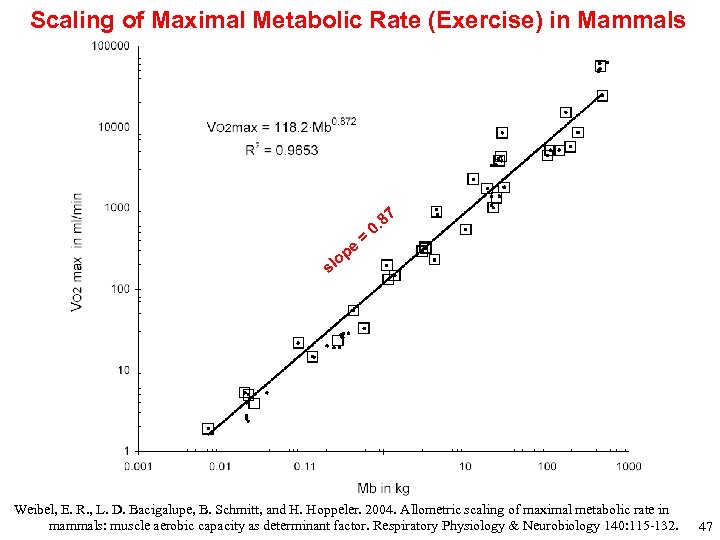Scaling of Maximal Metabolic Rate (Exercise) in Mammals pe = 87 0. o sl Weibel, E. R. , L. D. Bacigalupe, B. Schmitt, and H. Hoppeler. 2004. Allometric scaling of maximal metabolic rate in mammals: muscle aerobic capacity as determinant factor. Respiratory Physiology & Neurobiology 140: 115 -132. 47

What gives? Metabolic rate typically scales with an exponent less than unity, often ~ 0. 7 -0. 8 (many exceptions). Gas exchange surface area often scales with an exponent greater than 0. 67. But, the slopes do not always match. Example: mammalian maximal oxygen consumption (measured on motorized treadmill) scales as M 0. 872 whereas pulmonary diffusing capacity (measured morphometrically) scales as M 1. 084 So, large-bodied species have excess capacity. 48

Why the apparent excess capacity in large mammals? Presumably, other things vary allometrically, such as: blood volume blood oxygen carrying capacity (hemoglobin, hematocrit) oxygen unloading characteristics (shape of oxygen dissociation curve, e. g. , P 50) capillary densities capillary transit times mitochondrial volume densities 49

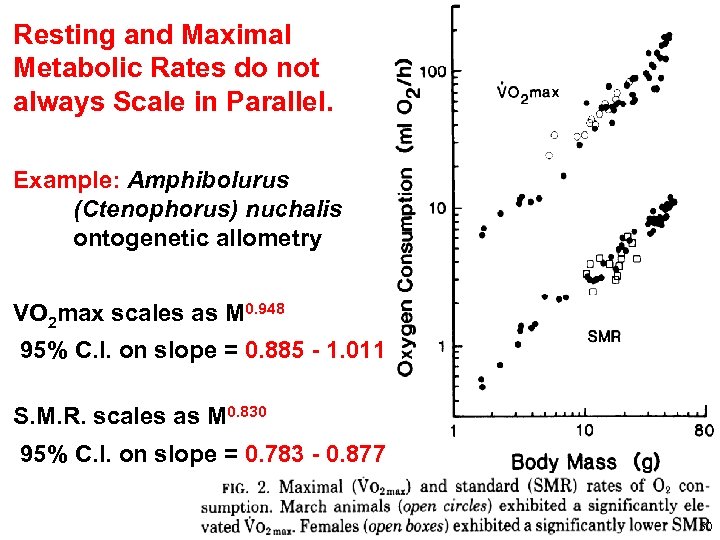Resting and Maximal Metabolic Rates do not always Scale in Parallel. Example: Amphibolurus (Ctenophorus) nuchalis ontogenetic allometry VO 2 max scales as M 0. 948 95% C. I. on slope = 0. 885 - 1. 011 S. M. R. scales as M 0. 830 95% C. I. on slope = 0. 783 - 0. 877 50

What about fasting endurance? All animals "fast" for some periods of time, even if it is just overnight. Based on what you have learned so far, how would you expect fasting endurance (how long they can fast) to vary with body size? What are the main components of fasting endurance? rate of energy use (metabolic rate) energy stores (stomach or crop contents, fat, glycogen, but also protein) In general, large animals should be able to fast for longer periods of time, and this is supported by empirical evidence, e. g. , Millar, J. S. , and G. J. Hickling. 1990. Fasting endurance and the evolution of mammalian body size. Functional Ecology 4: 5 -12. 51

Many Suborganismal Traits Vary Allometrically log Heart = 0. 791 + 0. 966 log Body Mass 95% C. I. on slope = (0. 951, 0. 982) So, the heart is a bit smaller, relatively speaking, in larger mammals. 181 Species of Mammals C: Heart 282. ppt 52

Using Allometry as a Tool to Understand Organismal Design and Adaptation Deviations from the empirical line of best fit, for a given kind of animal, may indicate special adaptations. Ex. : pronghorn have high maximal rate of oxygen consumption (VO 2 max) Ex. : humans have large brains As shown on next 2 slides … 53

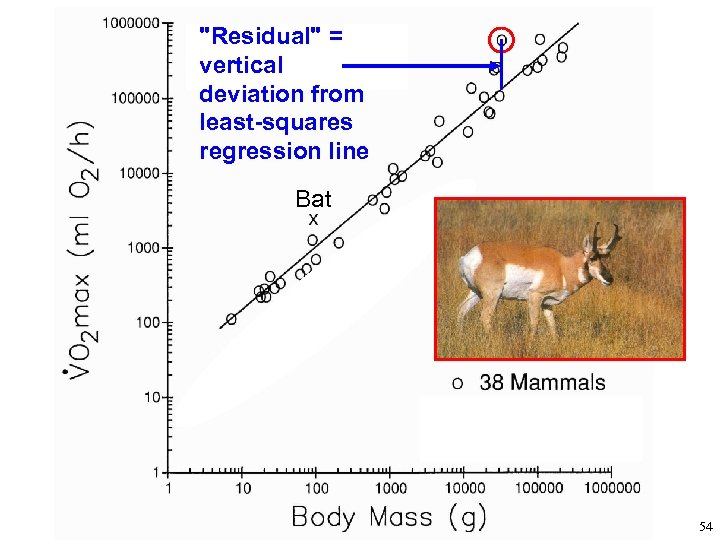"Residual" = vertical deviation from least-squares regression line Bat 54

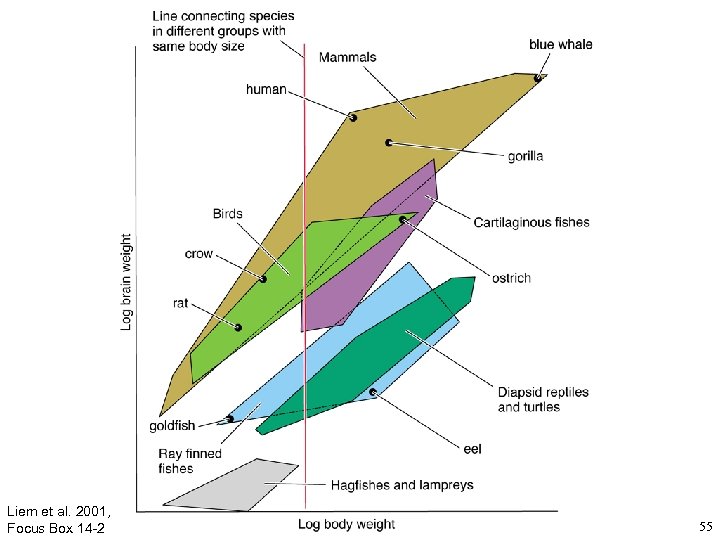Liem et al. 2001, Focus Box 14 -2 55

Using Allometry as a Tool to Understand Organismal Design and Adaptation These deviations call for explanations at both proximate and ultimate levels. Ultimate: Why did natural or sexual selection make them that way, or was it just random genetic drift? e. g. , apparently, increasing intelligence was favored in human ancestors e. g. , perhaps pronghorn use their high aerobic capacity when escaping from predators, or perhaps males "show off" for females 56

Using Allometry as a Tool to Understand Organismal Design and Adaptation Proximate: How do they do it in terms of morphology and physiology? e. g. , maybe pronghorn have large lungs, high hemoglobin levels, large hearts, lots of mitochondria in their muscles. . . 57

Metabolic Rate is Often Expressed per unit Mass of Tissue (e. g. , per gram body mass) If Whole-animal BMR M 0. 75 Then Mass-specific BMR M-0. 25 58

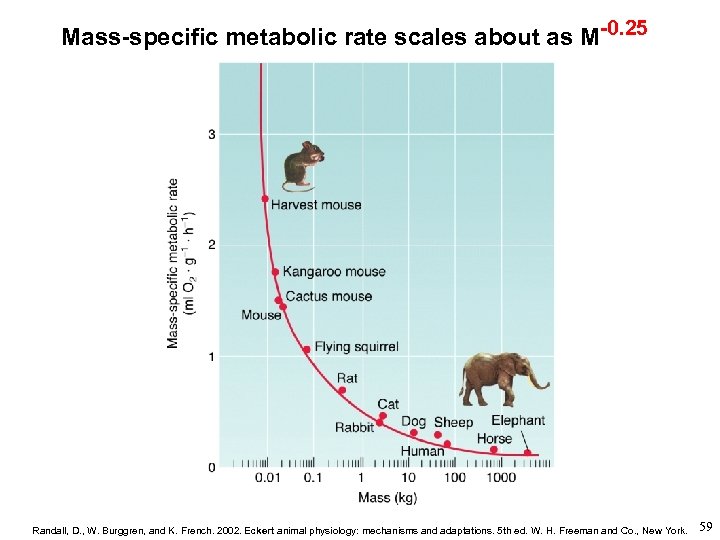Mass-specific metabolic rate scales about as M-0. 25 Randall, D. , W. Burggren, and K. French. 2002. Eckert animal physiology: mechanisms and adaptations. 5 th ed. W. H. Freeman and Co. , New York. 59

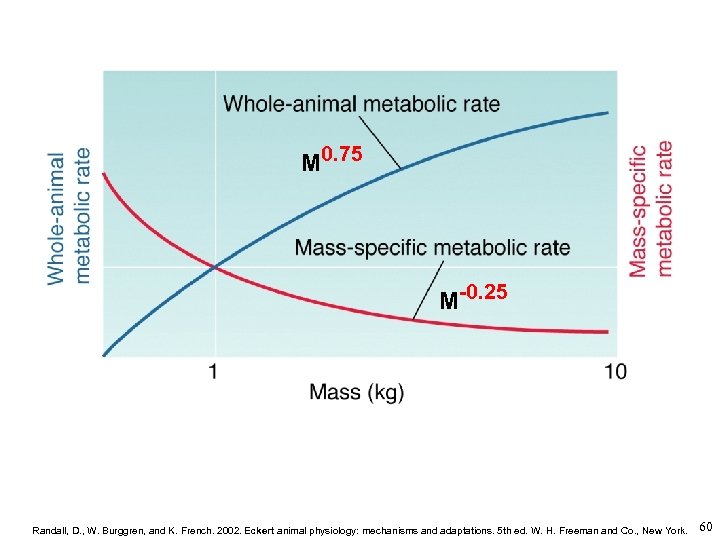M 0. 75 M-0. 25 Randall, D. , W. Burggren, and K. French. 2002. Eckert animal physiology: mechanisms and adaptations. 5 th ed. W. H. Freeman and Co. , New York. 60

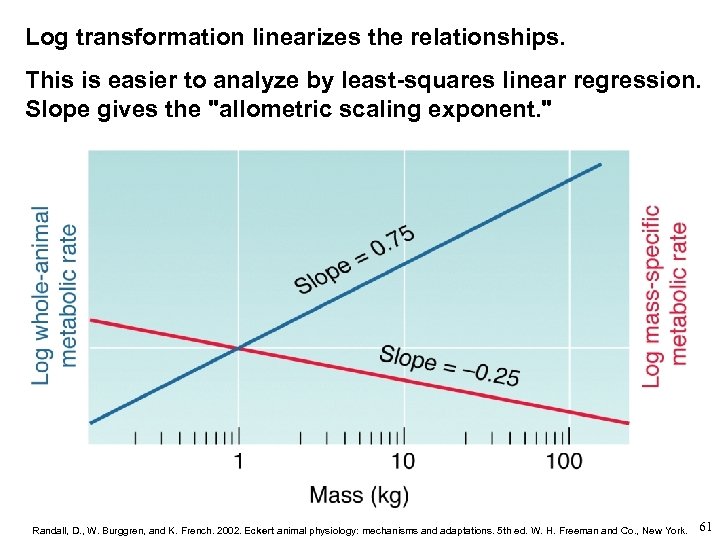Log transformation linearizes the relationships. This is easier to analyze by least-squares linear regression. Slope gives the "allometric scaling exponent. " Randall, D. , W. Burggren, and K. French. 2002. Eckert animal physiology: mechanisms and adaptations. 5 th ed. W. H. Freeman and Co. , New York. 61

Statistical Tutorial 62

Correlation (bivariate) - relationship between two traits or variables: Can be positive or negative Ranges from -1 to +1 Usually assumed to be linear for purposes of statistical testing Pearson product-moment correlation assumes bivariate normality; denoted as r or R Spearman rank correlation is a "nonparametric" alternative By itself, correlation does not indicate causation! 63

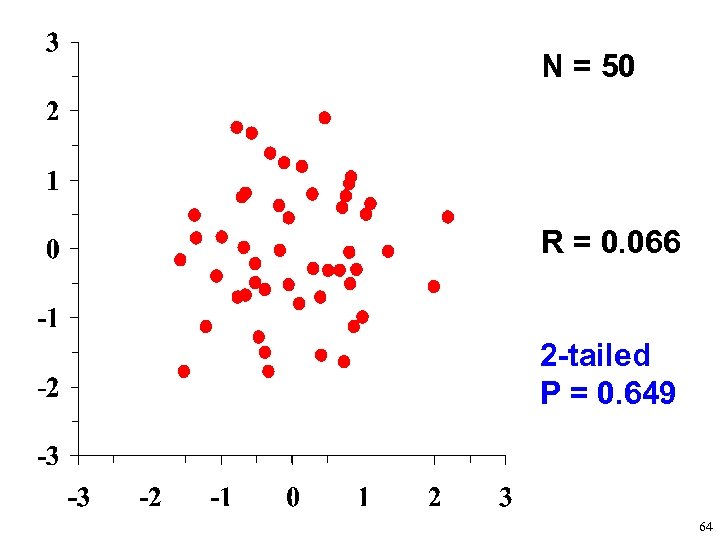N = 50 R = 0. 066 2 -tailed P = 0. 649 64

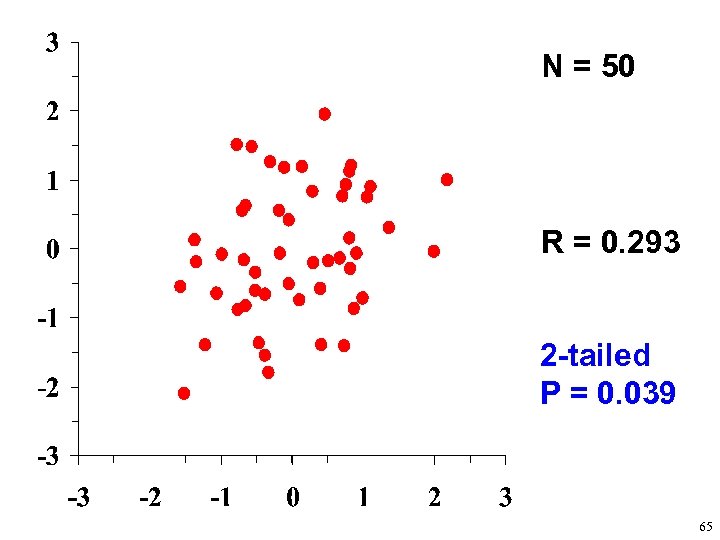N = 50 R = 0. 293 2 -tailed P = 0. 039 65

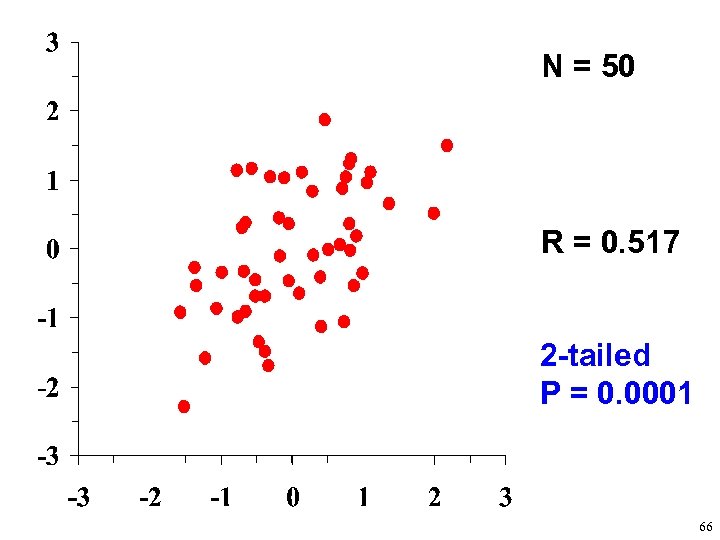N = 50 R = 0. 517 2 -tailed P = 0. 0001 66

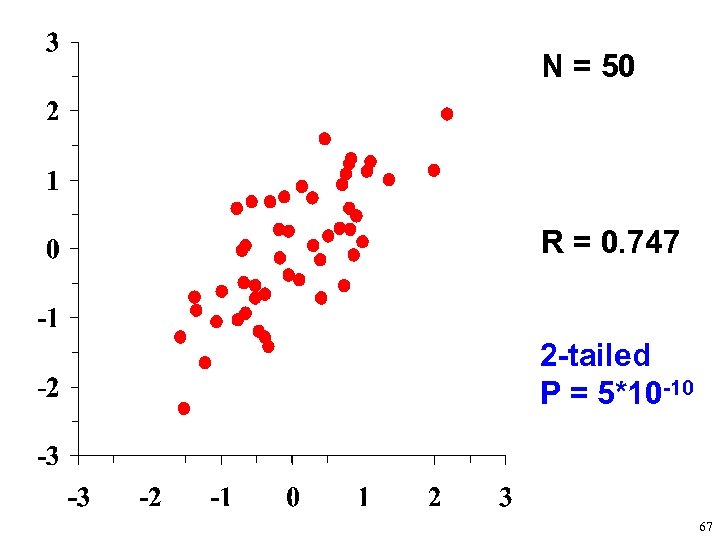N = 50 R = 0. 747 2 -tailed P = 5*10 -10 67

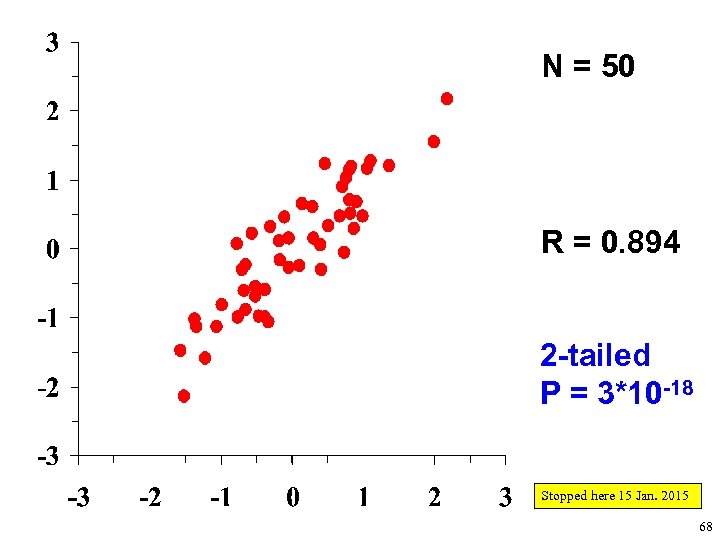N = 50 R = 0. 894 2 -tailed P = 3*10 -18 Stopped here 15 Jan. 2015 68

Regression - one type of line of best fit: More formally, "least-squares linear regression" Distinguishes between "dependent" (Y) and "independent" (X) variable Typically used when some degree of causality is presumed Minimizes sum of the squared vertical deviations from the line = residuals Passes through point mean X, mean Y Coefficient of determination (r 2 or R 2) indicates how much of the variance in Y is explained by variance in X Started here 20 Jan. 2015 69

Assumes no measurement error in the independent (X) variable If have measurement error in X variable, then underestimates the slope Not really appropriate in many biological studies (including allometry) but used anyway Various alternatives to ordinary least-squares (OLS) regression lines (sometimes called Model II regressions): (For more details, see: http: //www. unc. edu/courses/2007 spring/biol/145/001/docs/lectures/Nov 5. html) 70

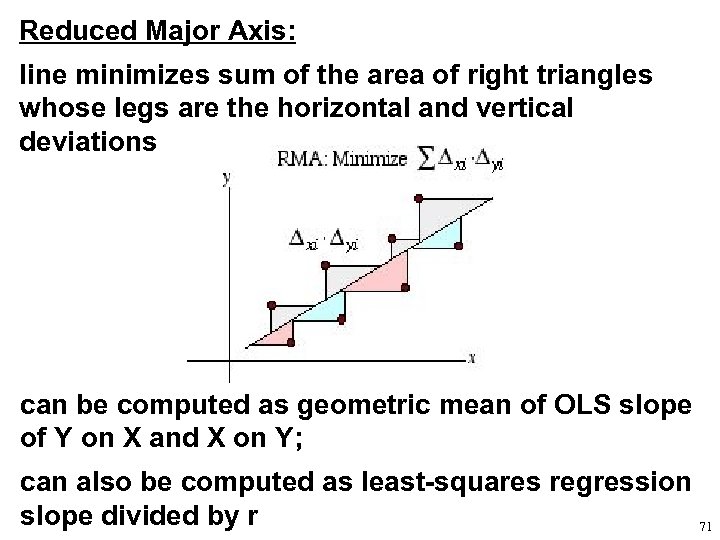Reduced Major Axis: line minimizes sum of the area of right triangles whose legs are the horizontal and vertical deviations can be computed as geometric mean of OLS slope of Y on X and X on Y; can also be computed as least-squares regression slope divided by r 71

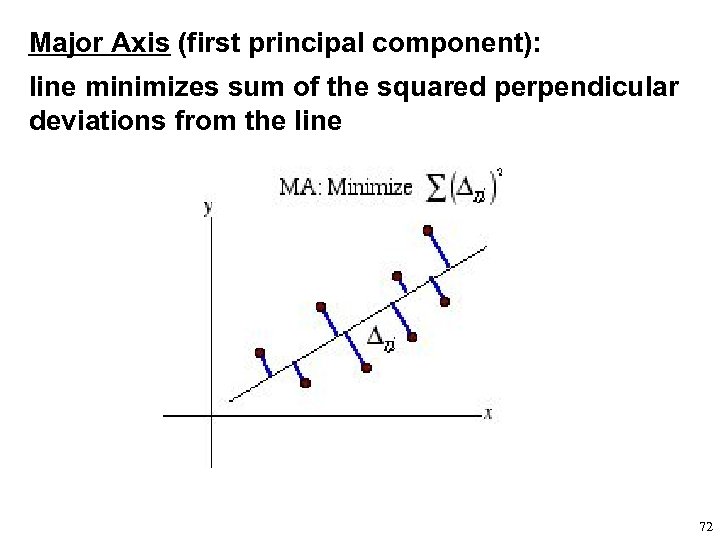Major Axis (first principal component): line minimizes sum of the squared perpendicular deviations from the line 72

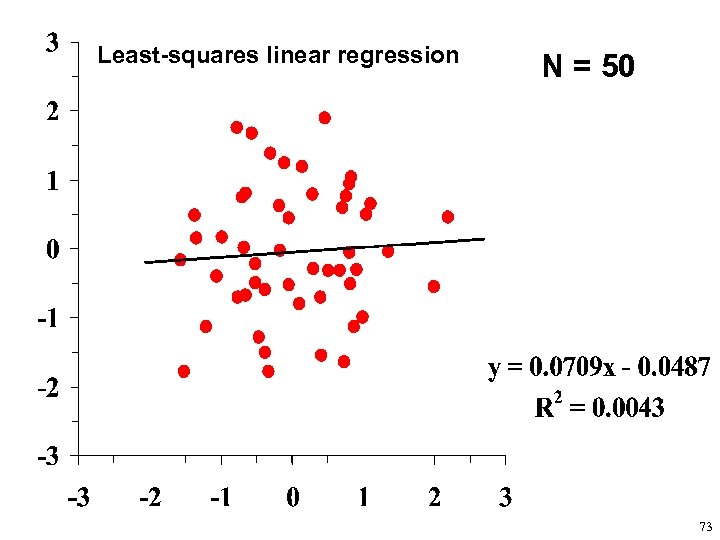Least-squares linear regression N = 50 73

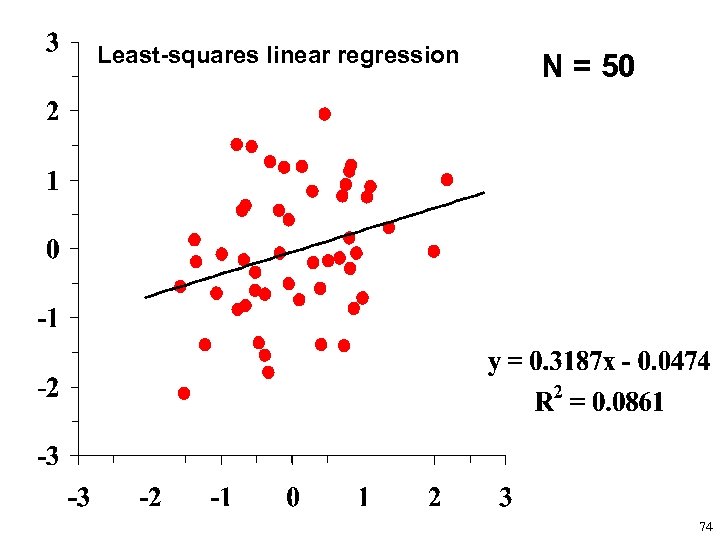Least-squares linear regression N = 50 74

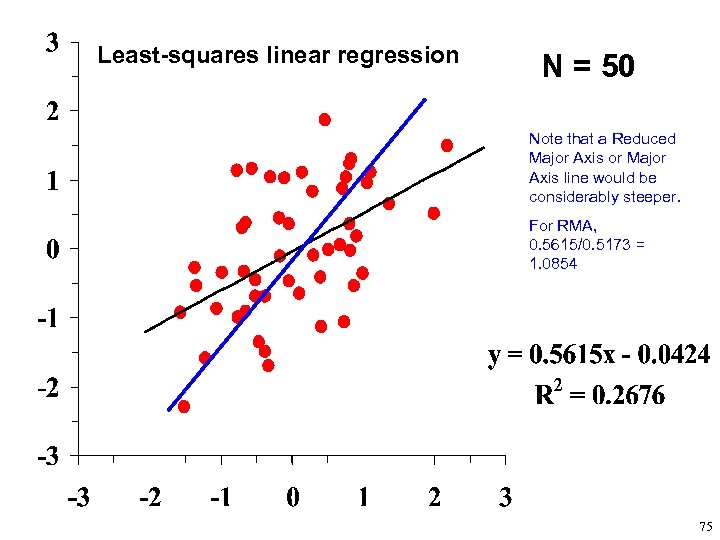Least-squares linear regression N = 50 Note that a Reduced Major Axis or Major Axis line would be considerably steeper. For RMA, 0. 5615/0. 5173 = 1. 0854 75

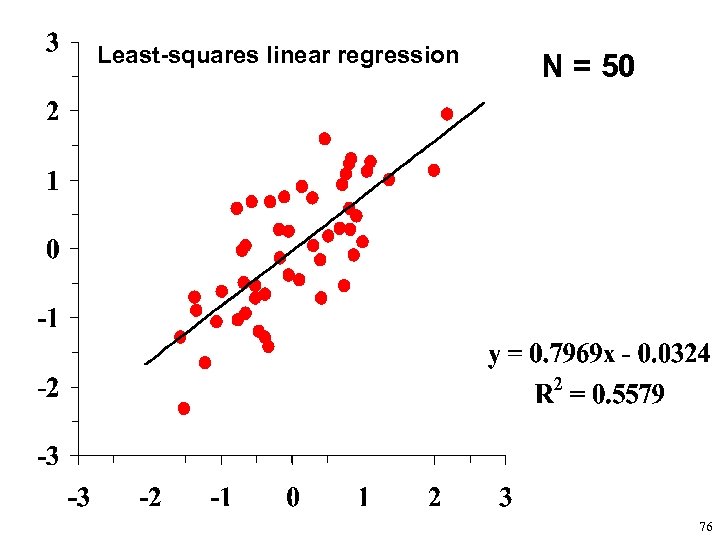Least-squares linear regression N = 50 76

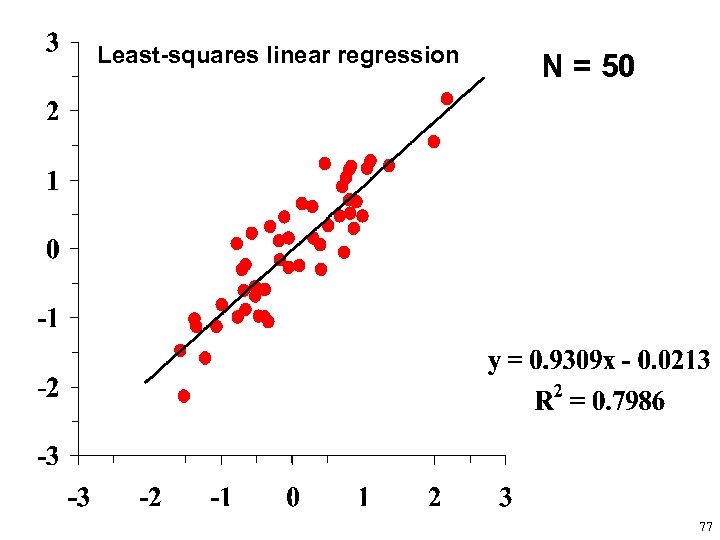Least-squares linear regression N = 50 77

Using Residuals to Factor out the Effects of Variation in Body Size: Often a better choice than using ratios, as shown in the following lizard example. 78

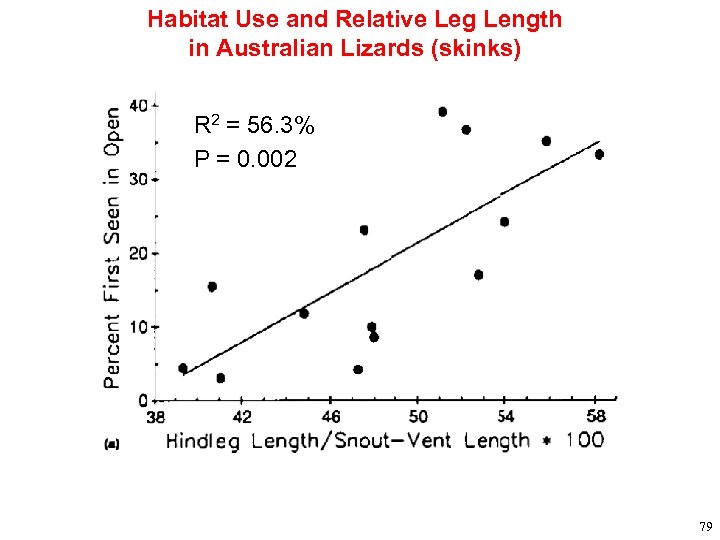Habitat Use and Relative Leg Length in Australian Lizards (skinks) R 2 = 56. 3% P = 0. 002 79

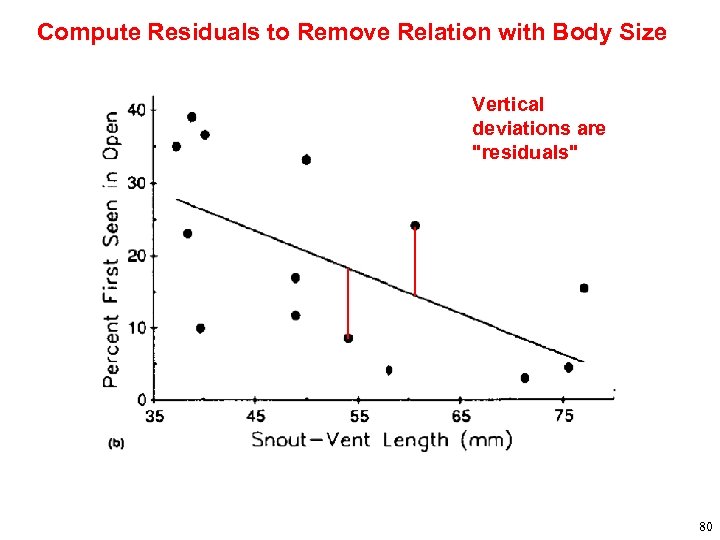Compute Residuals to Remove Relation with Body Size Vertical deviations are "residuals" 80

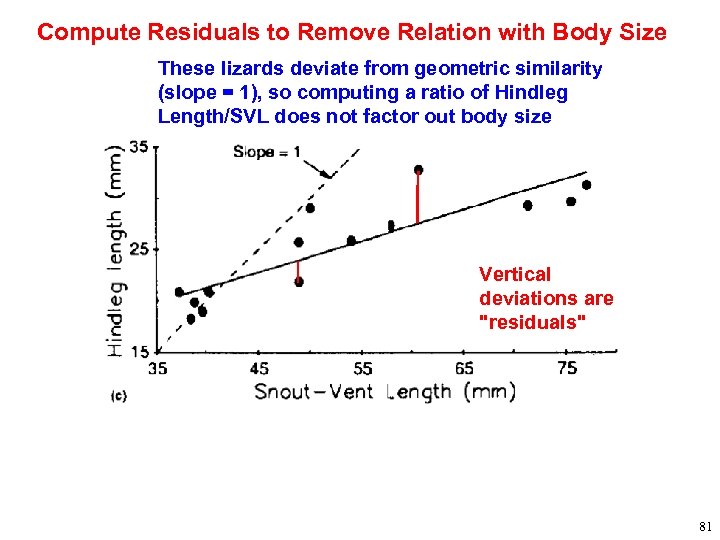Compute Residuals to Remove Relation with Body Size These lizards deviate from geometric similarity (slope = 1), so computing a ratio of Hindleg Length/SVL does not factor out body size Vertical deviations are "residuals" 81

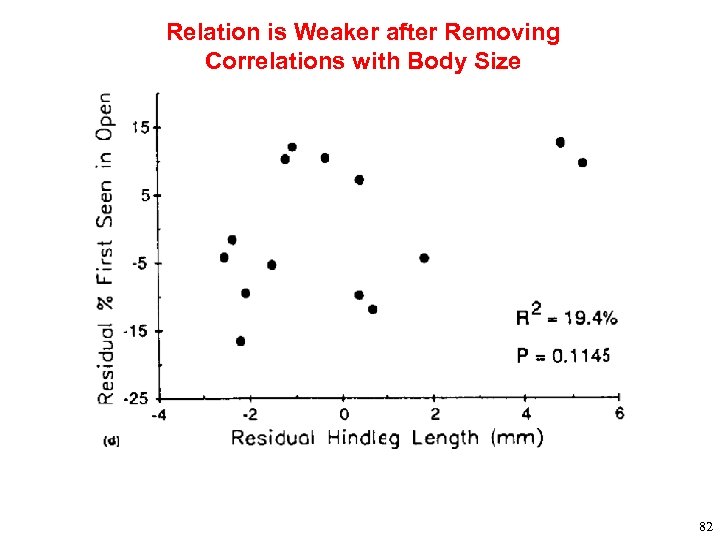Relation is Weaker after Removing Correlations with Body Size 82

t-test - statistical test based on the t distribution. Most commonly, a comparison of the mean (average) value of samples from two populations: Are the means "significantly" different? Statistically "significant" traditionally taken as P < 0. 05 1 in 20 chance of getting a difference that big by chance alone when you sample randomly from two populations that actually have the same mean 1 in 20 times you will get a "significant" difference when there really is not one, i. e. , commit a Type I error 83

ANOVA - statistical test used to compare mean values of 2 or more populations. Based on the F distribution. F = t squared. 84

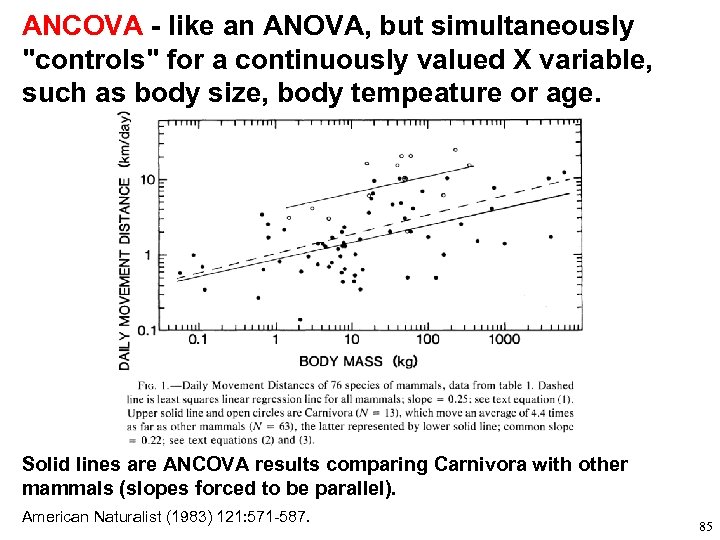ANCOVA - like an ANOVA, but simultaneously "controls" for a continuously valued X variable, such as body size, body tempeature or age. Solid lines are ANCOVA results comparing Carnivora with other mammals (slopes forced to be parallel). American Naturalist (1983) 121: 571 -587. 85

Extra Slides Follow. . . 86

Add something on: learning outcomes the scientific method levels of analysis MPBF proximate vs. ultimate causation 4 ways to study evolution: CM Biology of Natural Populations Selection Experiments Theoretical Models Plasticity? Epigenetics? https: //www. msu. edu/. . . /Methods&Levels. ppt from ZOL 313 May 14, 2008 87

4 Ways to Study Physiological Evolution 1. Phylogenetic Comparisons of Species (or populations) Shows what has happened in past evolution 2. Biology of Natural Populations: extent of individual variation (repeatability) heritability and genetic correlations natural and sexual selection field manipulations and introductions Shows present evolution in action 3. Selection Experiments Shows, experimentally, what might happen during future evolution 4. Compare Real Organisms with Theoretical Models Shows how close selection can get to producing optimal solutions 88

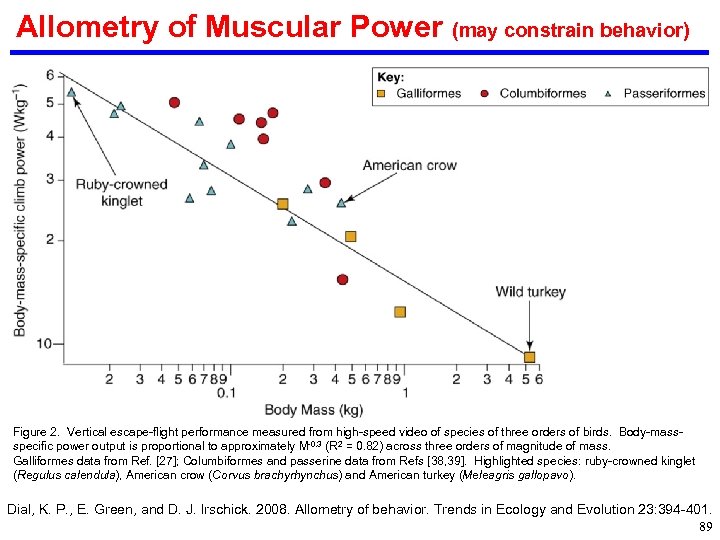Allometry of Muscular Power (may constrain behavior) Figure 2. Vertical escape-flight performance measured from high-speed video of species of three orders of birds. Body-massspecific power output is proportional to approximately M-0. 3 (R 2 = 0. 82) across three orders of magnitude of mass. Galliformes data from Ref. [27]; Columbiformes and passerine data from Refs [38, 39]. Highlighted species: ruby-crowned kinglet (Regulus calendula), American crow (Corvus brachyrhynchus) and American turkey (Meleagris gallopavo). Dial, K. P. , E. Green, and D. J. Irschick. 2008. Allometry of behavior. Trends in Ecology and Evolution 23: 394 -401. 89

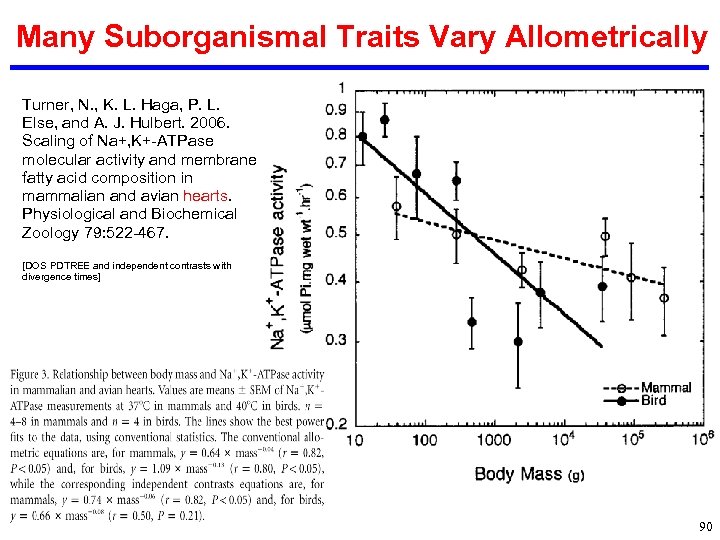Many Suborganismal Traits Vary Allometrically Turner, N. , K. L. Haga, P. L. Else, and A. J. Hulbert. 2006. Scaling of Na+, K+-ATPase molecular activity and membrane fatty acid composition in mammalian and avian hearts. Physiological and Biochemical Zoology 79: 522 -467. [DOS PDTREE and independent contrasts with divergence times] 90

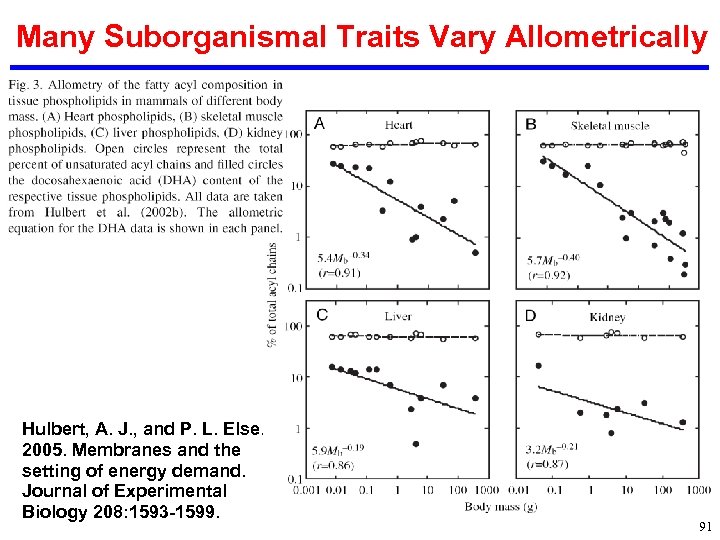Many Suborganismal Traits Vary Allometrically Hulbert, A. J. , and P. L. Else. 2005. Membranes and the setting of energy demand. Journal of Experimental Biology 208: 1593 -1599. 91

Borrell, B. J. 2007. Scaling of nectar foraging in orchid bees. American Naturalist 169: 569 -580. [independent contrasts in Mesquite, discussion of measurement error and RMA] Damuth, J. 2007. A macroevolutionary explanation for energy equivalence in the scaling of body Size and population density. American Naturalist 169: 621 -631. Millar, J. S. , and G. J. Hickling. 1990. Fasting endurance and the evolution of mammalian body size. Functional Ecology 4: 5 -12. Herrel, A. , and J. C. O’Reilly. 2006. Ontogenetic scaling of bite force in lizards and turtles. Physiological and Biochemical Zoology 79: 31 -42. 92

Jayne, B. C. , and A. F. Bennett. 1990. Scaling of speed and endurance in garter snakes: a comparison of cross-sectional and longitudinal allometries. J. Zool. , Lond. 220: 257 -277. Schilling, N. 2005. Ontogenetic development of locomotion in small mammals – a kinematic study. Journal of Experimental Biology 208: 4013 -4034. Schilling, N. , and A. Petrovitch. 2006. Postnatal allometry of the skeleton in Tupaia glis (Scandentia: Tupaiidae) and Galea musteloides (Rodentia: Caviidae) – A test of the three-segment limb hypothesis. Zoology 109: 148 -163. Carpenter, F. L. , and R. E. Mac. Millen. 1976. Energetic cost of feeding territories in an Hawaiian honeycreeper. Oecologia 26: 213 -223. Mac. Millen, R. E. 1981. Nonconformance of standard metabolic rate with body mass in Hawaiian Honeycreepers. Oecologia 49: 340 -343. Hulbert, A. J. , and R. E. Mac. Millen. 1988. The influence of ambient temperature, seed composition and body size on water balance and seed selection in coexisting heteromyid rodents. Oecologia 75: 521 -526. Lawhon, D. K. , and M. S. Hafner. 1981. Tactile discriminatory ability and foraging strategies in kangaroo rats and pocket mice (Rodentia: Heteromyidae). Oecologia (Berlin) 50: 303 -309. Price, M. V. , and K. M. Heinz. 1984. Effects of body size, seed density, and soil characteristics on rates of seed harvest by heteromyid rodents. Oecologia 61: 420 -425. Mac. Millen, R. E. , and D. S. Hinds. 1983. Water regulatory efficiency in heteromyid rodents: a model and its application. Ecology 64: 152 -164. Morton, S. R. , D. S. Hinds and R. E. Mac. Millen. 1980. Cheek pouch capacity in heteromyid rodents. Oecologia 46: 143 -146. 93

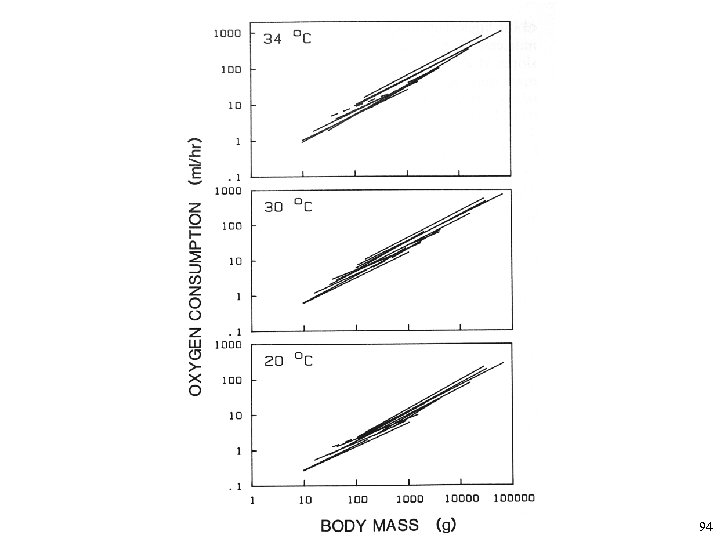94

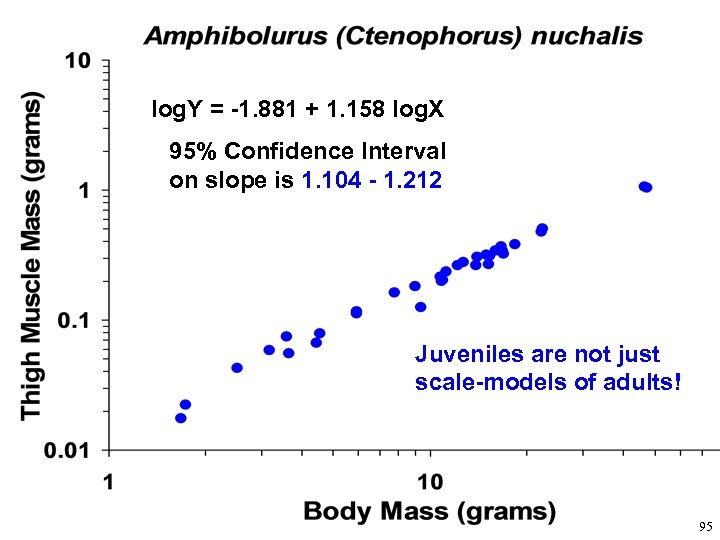log. Y = -1. 881 + 1. 158 log. X 95% Confidence Interval on slope is 1. 104 - 1. 212 Juveniles are not just scale-models of adults! 95

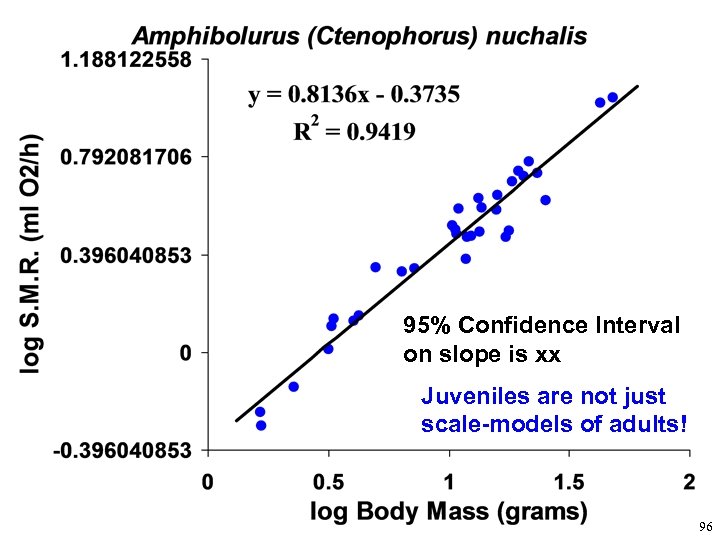95% Confidence Interval on slope is xx Juveniles are not just scale-models of adults! 96

Examples of evolutionary (interspecific) allometry … we will return to this later. . . 97

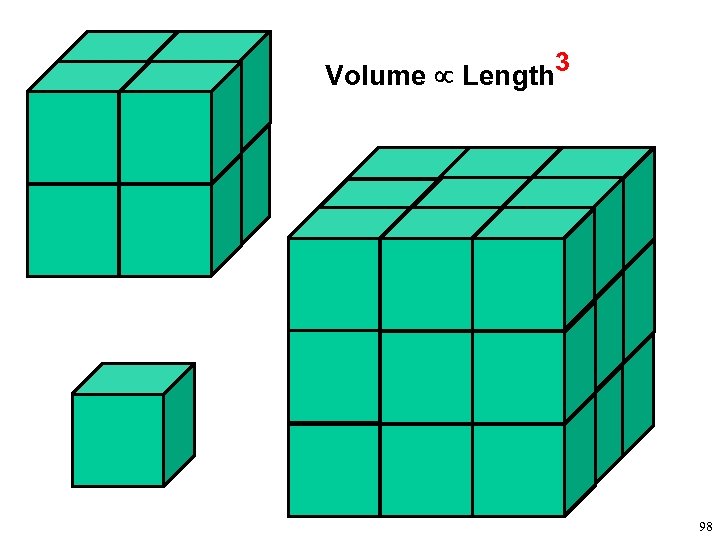Volume Length 3 98