Lecture 3 Manufacturing Scheduling Concepts J Christopher

Lecture 3: Manufacturing Scheduling Concepts © J. Christopher Beck 2005 1

Outline n Jobs & Operations n n Resources/machines n n n Characteristics & notation Setup/transition cost Objective functions Complexity © J. Christopher Beck 2005 2

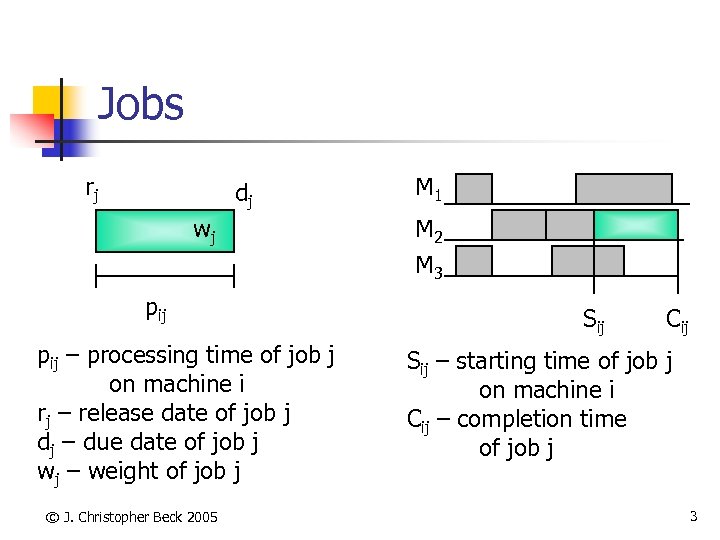Jobs rj dj wj pij – processing time of job j on machine i rj – release date of job j dj – due date of job j wj – weight of job j © J. Christopher Beck 2005 M 1 M 2 M 3 Sij Cij Sij – starting time of job j on machine i Cij – completion time of job j 3

Jobs & Operations n Often jobs are made up of a set of operations rj dj wj p 2 j p 0 j p 3 j p 1 j precedence constraints © J. Christopher Beck 2005 4

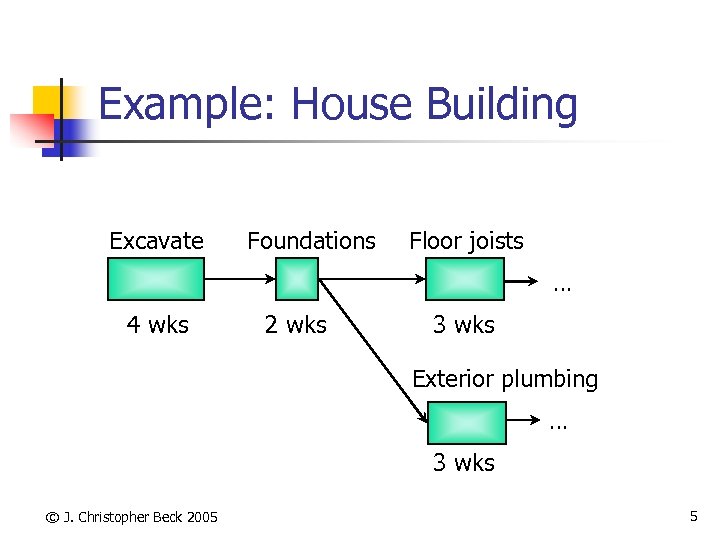Example: House Building Excavate Foundations Floor joists … 4 wks 2 wks 3 wks Exterior plumbing … 3 wks © J. Christopher Beck 2005 5

Resources/Machines n Jobs may need resources n n Mixing machine, back-hoe, cement mixer May be multiple similar resources are available and you need to choose one © J. Christopher Beck 2005 6

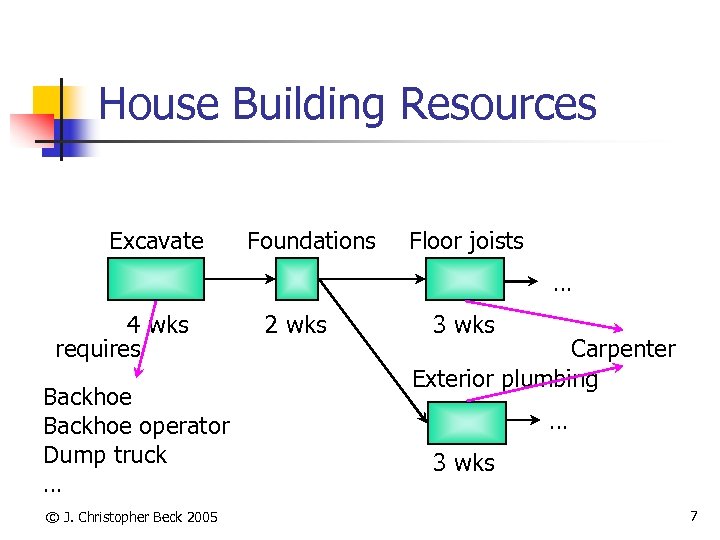House Building Resources Excavate Foundations Floor joists … 4 wks requires Backhoe operator Dump truck … © J. Christopher Beck 2005 2 wks 3 wks Carpenter Exterior plumbing … 3 wks 7

Resources & Setup n n If 2 jobs need the same resource (and the resource can only do 1 thing at a time), then the jobs must be sequenced May be a time or cost for a resource to change jobs (“sequence dependent setup”) © J. Christopher Beck 2005 8

Objectives n Minimize maximum completion time (aka “makespan”) n n n Min Cmax = max(C 1, … Cn) Minimize maximum lateness n n Min Lmax = max(C 1 – d 1, … Cn – dn) © J. Christopher Beck 2005 9

Objectives n Minimize total weighted tardiness n n Min Σwj. Tj Tj = max(Cj – dj, 0) © J. Christopher Beck 2005 10

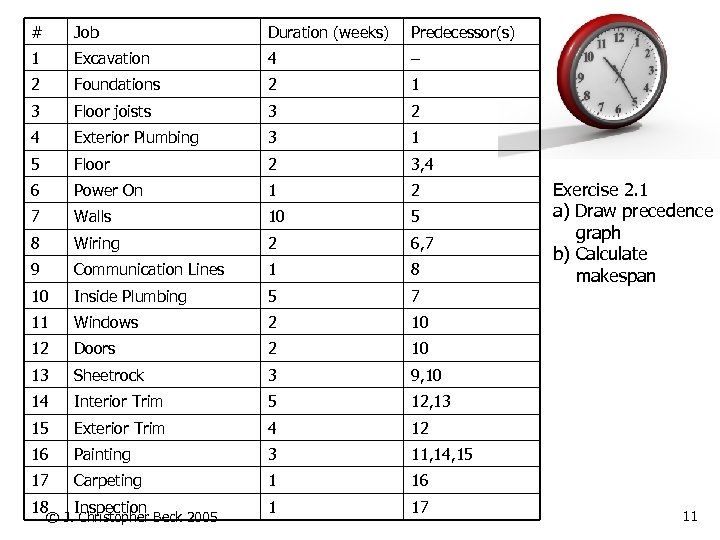# Job Duration (weeks) Predecessor(s) 1 Excavation 4 – 2 Foundations 2 1 3 Floor joists 3 2 4 Exterior Plumbing 3 1 5 Floor 2 3, 4 6 Power On 1 2 7 Walls 10 5 8 Wiring 2 6, 7 9 Communication Lines 1 8 10 Inside Plumbing 5 7 11 Windows 2 10 12 Doors 2 10 13 Sheetrock 3 9, 10 14 Interior Trim 5 12, 13 15 Exterior Trim 4 12 16 Painting 3 11, 14, 15 17 Carpeting 1 16 18 Inspection 1 17 © J. Christopher Beck 2005 Exercise 2. 1 a) Draw precedence graph b) Calculate makespan 11

Hard Problems vs. Easy Problems n n Exercise 2. 1 b was “easy” Adding resources would have made it hard Hard & easy have precise mathematical definitions You need to have, at least, an intuitive understanding of what this means © J. Christopher Beck 2005 12

Hard vs Easy n Easy: n n n Sort n numbers Solve a system of linear equations Hard: n Schedule a factory, deliver packages, schedule buses, … © J. Christopher Beck 2005 13

Hard vs Easy n n f (n): the number of “basic operations” needed to solve the problem with input size n Easy: f (n) is polynomial in n O(n), O(n log n), O(n 2), … Hard: f (n) is exponential in n n O(2 n), … © J. Christopher Beck 2005 14

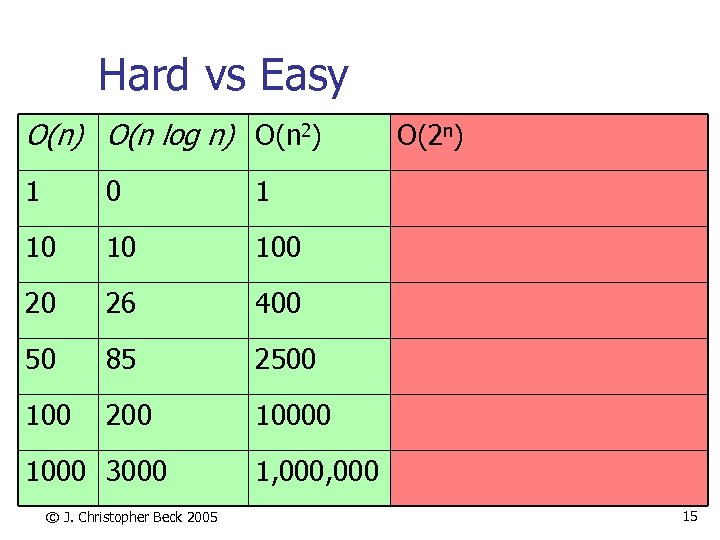Hard vs Easy O(n) O(n log n) O(n 2) 1 0 1 10 10 100 20 26 400 50 85 2500 100 200 O(2 n) 10000 1000 3000 © J. Christopher Beck 2005 1, 000 15

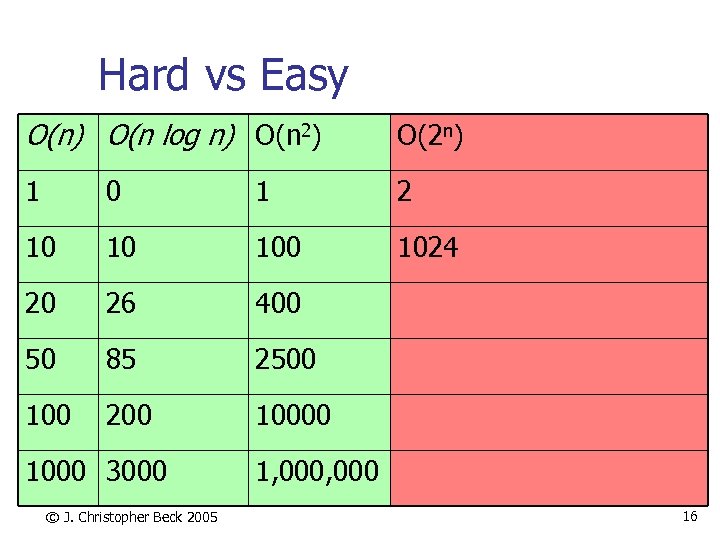Hard vs Easy O(n) O(n log n) O(n 2) O(2 n) 1 0 1 2 10 10 1024 20 26 400 50 85 2500 100 200 1000 3000 © J. Christopher Beck 2005 1, 000 16

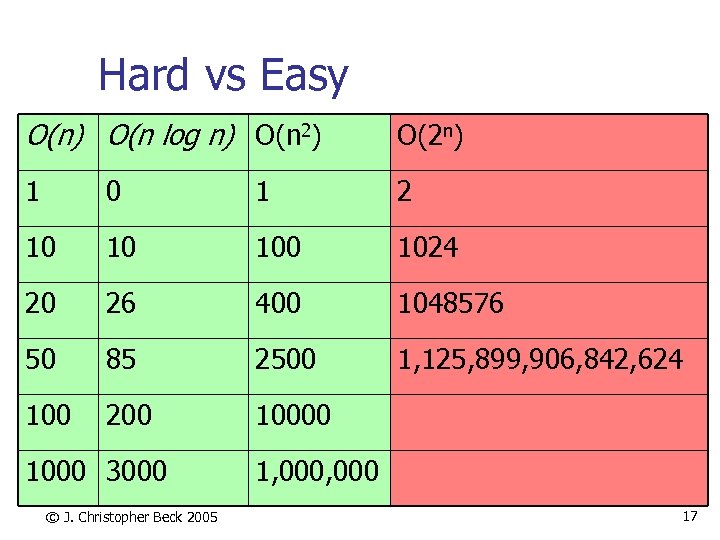Hard vs Easy O(n) O(n log n) O(n 2) O(2 n) 1 0 1 2 10 10 1024 20 26 400 1048576 50 85 2500 1, 125, 899, 906, 842, 624 100 200 1000 3000 © J. Christopher Beck 2005 1, 000 17

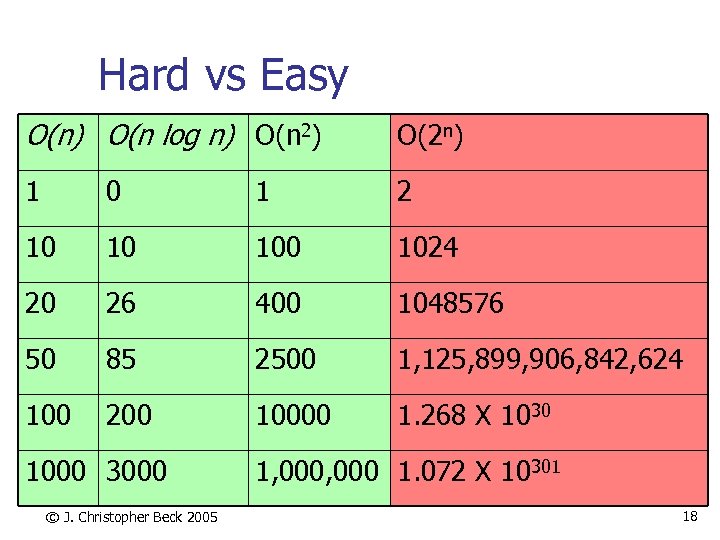Hard vs Easy O(n) O(n log n) O(n 2) O(2 n) 1 0 1 2 10 10 1024 20 26 400 1048576 50 85 2500 1, 125, 899, 906, 842, 624 100 200 10000 1. 268 X 1030 1000 3000 © J. Christopher Beck 2005 1, 000 1. 072 X 10301 18

Hard vs Easy n n 10301 operations required in worst case Age of universe: 1018 seconds Fastest Computer today: 1014 op/sec Let’s say we get a computer 1018 times faster (a sextillion times faster) n n 1033 op/sec It may still take 10250 times longer than the age of the universe to solve the problem! © J. Christopher Beck 2005 19

Hard vs Easy n If it is going to take 10250 times the age of the universe to schedule a factory, why bother? © J. Christopher Beck 2005 20

Hard vs Easy n If it is going to take 10250 times the age of the universe to schedule a factory, why bother? n n May be we can do it in a reasonable time in most cases? May be we can get a good (but not necessarily best possible) solution in a reasonable amount of time? © J. Christopher Beck 2005 21