Lecture 3 Kinematics Mechanics At the end

Lecture 3 – Kinematics (Mechanics) At the end of this lecture you should Understand: displacement and distance, velocity and speed, acceleration, including their differential forms Have: the equations of motion for constant acceleration ( all five ‘suvat’ equations) Use: the ‘suvat’ equations to solve problems involving moving objects. Be able to use: velocity-time graphs and displacementtime graphs to find the acceleration and distance travelled of moving objects Understand: what is meant by projectile motion and know a good method with which to approach such problems. Have: Lecture Notes that are useful and legible

Introduction to Mechanics (Kinematics) Kinematics (Mechanics)

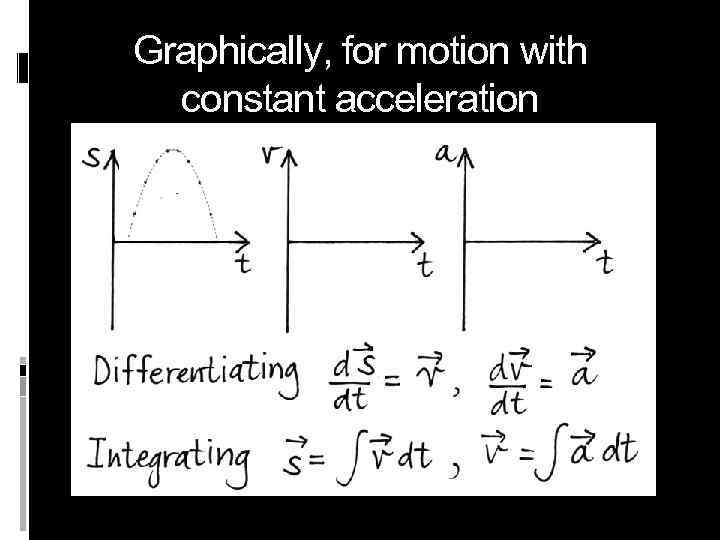Graphically, for motion with constant acceleration

Calculus in physics For vectors, differentiating displacement gives velocity; differentiating velocity gives acceleration. Conversely, integrating velocity gives displacement. For scalars, differentiating distance gives speed; differentiating speed gives acceleration. Conversely, integrating speed gives distance. For CPS physics, we will use calculus after it has been taught – in depth – in mathematics.

Acceleration-Deceleration

Equations for motion with constant acceleration s = ½(u+v)t What are the other ‘suvat’ equations?

Example 1. Velocity-time graph A tennis ball is dropped from a point, P. It falls to the ground and bounces back with half the speed with which it hit the ground. a) Draw a velocity-time graph of the motion b) Mark the point which shows the ball hitting the ground on your graph

Example 2. Using ‘suvat’ equations A man is driving his Mercedes at 20 m s-1 when he sees a girl crossing the road, 45 m ahead. The instant he sees her, he applies the brakes, which give him a constant deceleration of 5 m s-2. Will he avoid the girl?

Example 3. Combining graphs and equations A car is moving along a straight, horizontal road at constant speed 18 m s-1. At the instant the car passes a lay-by, a motorcyclist leaves the lay-by from rest and moves towards the car at constant acceleration, a = 2. 5 ms-2. Given that the motorcycle overtakes the car T seconds after leaving the lay-by, draw a velocity-time graph to calculate the following: a) the value of T b) the speed of the motorcycle when it passes the car

Projectile Motion Projectile motion is motion during which the only force acting on the object is gravity. Recall – for problems about projectile motion, we divide the data into two components: vertical and horizontal.

Example 4. Projectile motion At Acapulco, divers dive from 36 m up, down into the sea. At the bottom of the dive, a rock ledge sticks out 6. 4 m. What is the minimum horizontal velocity of the diver if he is to avoid the rocks?

Example 5 Show that the maximum range of a projectile of fixed initial speed is obtained when it is launched at an angle of 45º to the horizontal.

READING CHECK LIST Adams and Allday: 3. 1, 3. 2, 3. 10. At the end of this lecture you should Understand what is meant by displacement and distance, velocity and speed, acceleration, including their differential forms Have revised the equations of motion for constant acceleration (‘suvat’ equations) Be able to use velocity-time graphs and displacement-time graphs to find the acceleration and distance travelled of moving objects Use the equations of motion for constant acceleration to solve problems involving moving objects. Understand what is meant by projectile motion and know a good method with which to approach such problems.