Lecture 23 Introduction to Quantum Physics 1 L

Lecture 23 Introduction to Quantum Physics 1 L 23. Outline: 1. 1 - quantum physics, black body radiation; 1. 2 - Planck’s theory; 2. 0 - photoelectric effect, 3. 0 - Einstein's explanation of the photoelectric effect; 4. 0 - wave particle duality; 5. 0 - Heisenberg’s uncertainty principle; 1

1. Quantum Physics – Introduction • By the end of the 19 th century, the properties of matter were explained by using a particle model and a wave-based model; • Classical physics (i. e. Newton’s Mechanics, Maxwell’s Electromagnetism or the classical theory of thermal radiation) cannot explain the behaviour of matter on the atomic level e. g. black body radiation or the photoelectric effect; • Planck introduced the earliest ideas of Quantum Physics, and he was followed by Einstein, Bohr, Schrodinger, de Broglie, Heisenberg, Born and Dirac. 2

1. 1 Black Body Radiation • A black body is an ideal system that absorbs all radiation incident on it. • A hollow object with a small hole in its walls behaves like a black body; • The nature of the radiation leaving the cavity through the hole depends only on the temperature of its walls. . 3

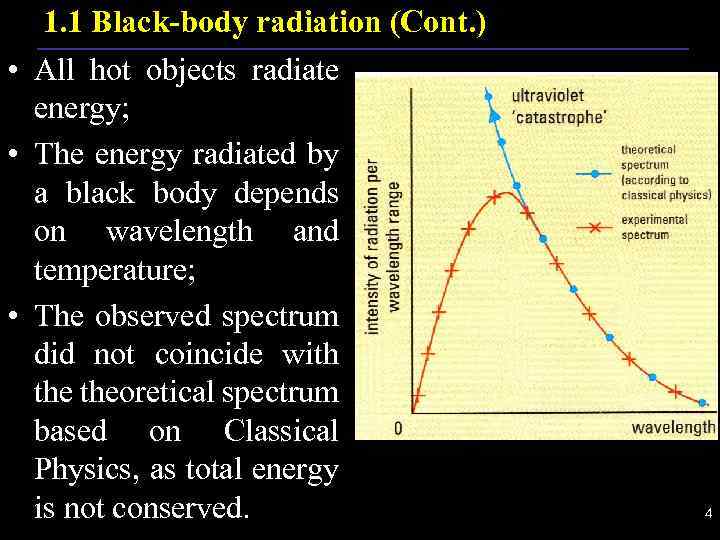1. 1 Black-body radiation (Cont. ) • All hot objects radiate energy; • The energy radiated by a black body depends on wavelength and temperature; • The observed spectrum did not coincide with theoretical spectrum based on Classical Physics, as total energy is not conserved. . 4

1. 2 Introducing Planck • Max Planck, a German physicist, solved the black body radiation problem in 1900, by introducing the revolutionary concept of “Energy Quanta”; • Thus energy is absorbed or emitted by an object in discrete amounts (quanta). 5

1. 2. 1 Planck’s Explanation • Planck developed a theory of blackbody radiation that leads to an equation for the intensity of the radiation; • This equation is in complete agreement with experimental observations; • Planck made two assumptions about the nature of the oscillators in the cavity walls 6

1. 2. 2 Planck’s Assumptions • The cavity radiation came from atomic oscillations in the cavity walls • The energy difference between the initial and final states of these atomic oscillators is emitted or absorbed as a single quantum of radiation. 7

1. 2. 2 Planck’s Assumptions (Cont. ) • All oscillators emit or absorb quantised amounts of radiation. That is, radiation comes in discrete packets or quanta. The energy of these quanta is proportional to frequency: E=hf (eq. 1) h = 6. 63 × 10 -34 Js is Planck’s constant also h = 4. 14 × 10 -15 e. Vs 8

The Electron-Volt h = 6. 63 × 10 -34 Js = 4. 14 × 10 -15 e. Vs A unit of energy equal to the work done on an electron in moving it through a potential difference of one volt. It is used as a measure of particle energies although it is not an SI unit. (Oxford Dictionary of Physics). 1 e. V = 1. 60 × 10 -19 J 9

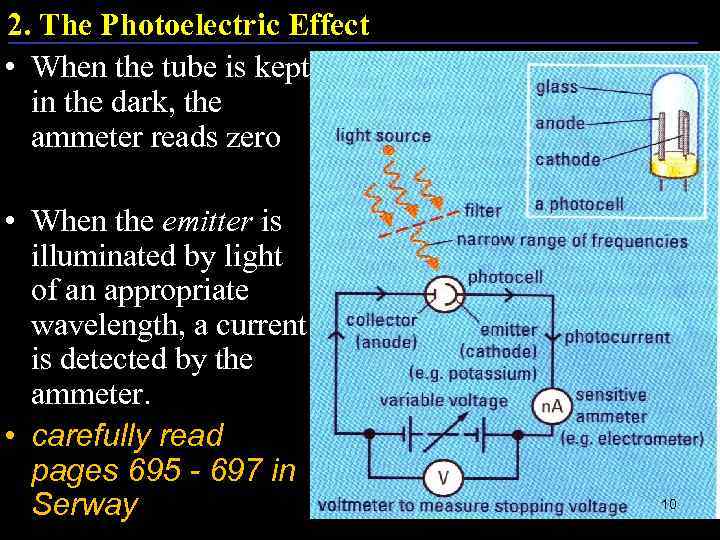2. The Photoelectric Effect • When the tube is kept in the dark, the ammeter reads zero • When the emitter is illuminated by light of an appropriate wavelength, a current is detected by the ammeter. • carefully read pages 695 - 697 in Serway 10

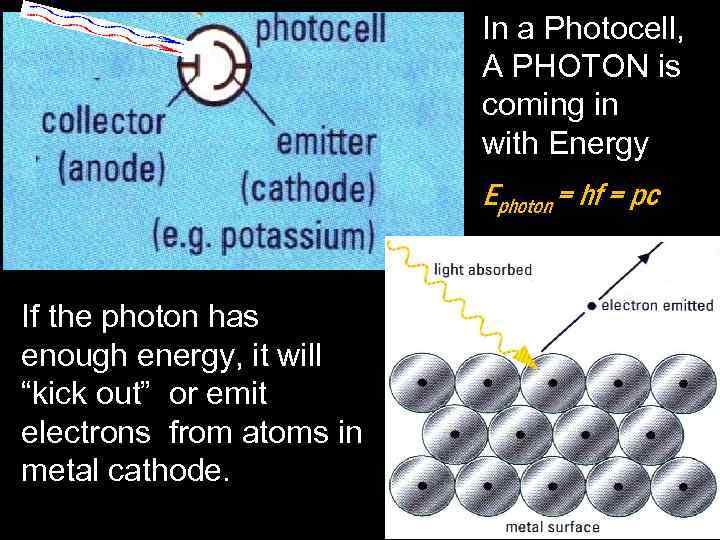In a Photocell, A PHOTON is coming in with Energy Ephoton = hf = pc If the photon has enough energy, it will “kick out” or emit electrons from atoms in metal cathode.

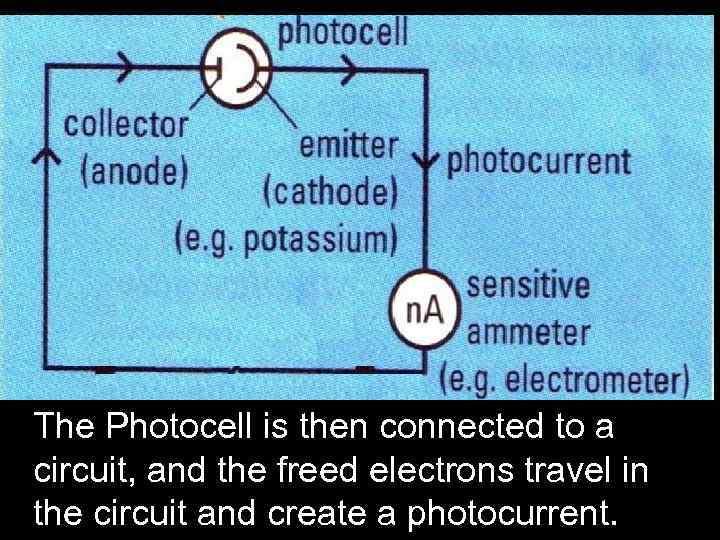The Photocell is then connected to a circuit, and the freed electrons travel in the circuit and create a photocurrent.

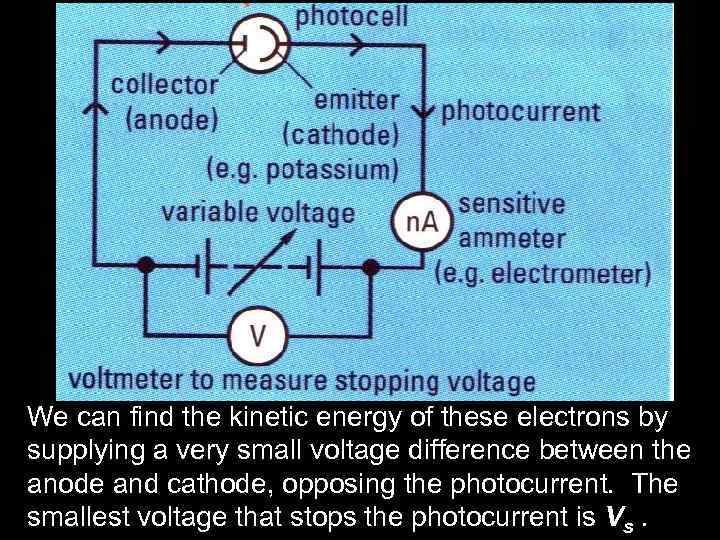We can find the kinetic energy of these electrons by supplying a very small voltage difference between the anode and cathode, opposing the photocurrent. The smallest voltage that stops the photocurrent is Vs.

2. The Photoelectric Effect (Cont. ) • The current arises from photoelectrons emitted from the negative plate and collected at the positive plate; • For each metal, there is a threshold frequency below which no electrons are emitted; • The number of electrons emitted is proportional to intensity of radiation; • Emitted electrons have KE up to a maximum value, which depends on the frequency of radiation (unexplained by classical physics). 14

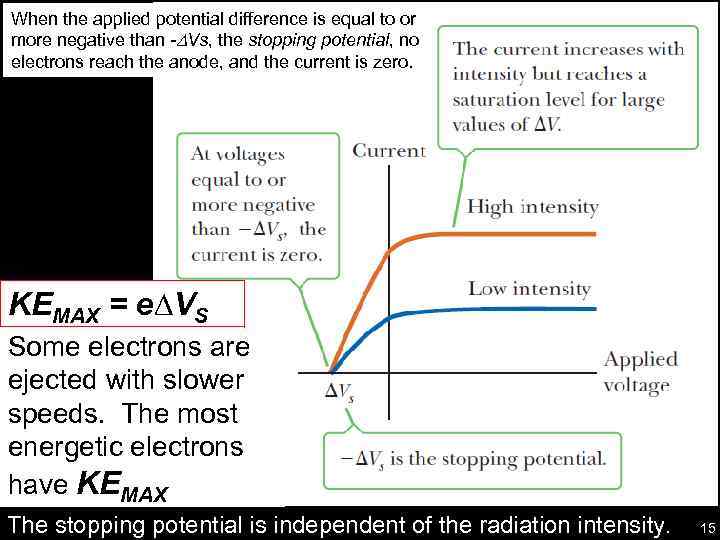When the applied potential difference is equal to or more negative than -DVs, the stopping potential, no electrons reach the anode, and the current is zero. KEMAX = e∆VS Some electrons are ejected with slower speeds. The most energetic electrons have KEMAX The stopping potential is independent of the radiation intensity. 15

3. Albert Einstein and the Photoelectric Effect • Einstein extended Planck’s energy quanta concept to electromagnetic waves; • Thus one photon is absorbed by one electron, providing it with the necessary energy to escape the atom as a photoelectron; • He was awarded the Nobel Prize for Physics in 1922. 16

3. Einstein’s Explanation (Cont. ) • Einstein suggested: (eq. 2) • is the “Work-Function” i. e. the threshold (minimum) photon energy required to release one electron from the surface of the metal. 17

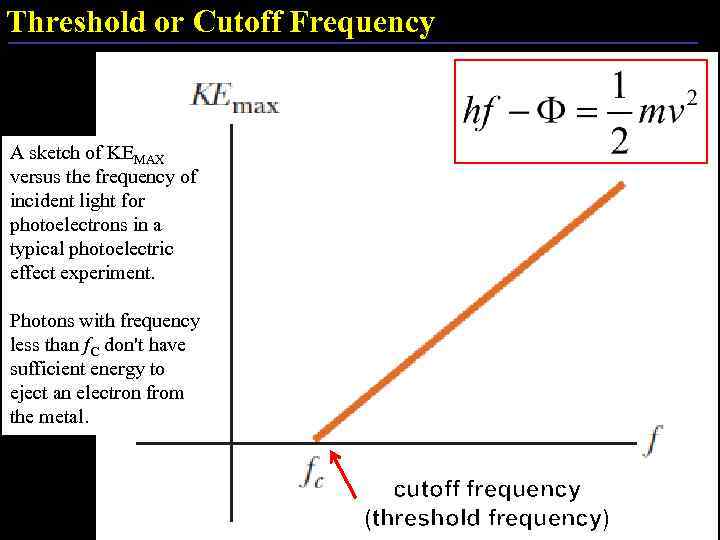Threshold or Cutoff Frequency A sketch of KEMAX versus the frequency of incident light for photoelectrons in a typical photoelectric effect experiment. Photons with frequency less than f. C don't have sufficient energy to eject an electron from the metal. cutoff frequency (threshold frequency) 18

Example 1 a) Find the longest wavelength beyond which no electrons are emitted from a caesium atom if ΦCS = 1. 80 e. V. b) If the surface is illuminated with monochromatic light of wavelength λ = 450 nm, calculate KEmax of emitted photoelectrons. c) What is the stopping potential which just prevents photoemission in b) ? 19

4. Wave-particle Duality • In his Ph. D thesis, Louis de Broglie postulated that all forms of matter have wave and particle properties: • Another “easy” Nobel Prize (1929) following the Davisson - Germer experimental confirmation of the electron waves diffraction. 20

4. 1 Electron and X-ray Diffraction • Diffraction patterns due to electron-waves (left) and X-rays (right) passing through aluminium foil. 21

4. 2 Further on matter waves • Why can’t we see the waves associated with big masses? 22

4. 3 Principle of Complementarity • The principle of complementarity states that the wave and particle models complement each other e. g. sometimes light behaves like a wave or as a particle; • Both models must be used in order to provide a complete description of a phenomenon. However, it is not possible to model both the wave and particle properties simultaneously; • Niels Bohr (1927). 23

5. Heisenberg’s Uncertainty Principle • Werner Heisenberg showed that: • Δx is the uncertainty in the position of a particle; • Δp is the uncertainty in its momentum. 24

Example 2 – Heisenberg’s Uncertainty Principle Suppose an electron is found somewhere in an atom of diameter 1. 25 × 10 -10 m. Estimate the uncertainty in the electron’s momentum (in one dimension). 25

LECTURE CHECK LIST LECTURE 23 – Introduction to Quantum Physics READING Serway, Chapter 27 Adams and Allday 8. 4 -7 At the end of this lecture you should: • Understand the quantum nature of the black body radiation; • Understand the photoelectric effect and the relevant formulas; • Understand wave-particle duality and the uncertainty principle; Answers: 1. ) a. ) 690 nm, b. ) 0. 960 e. V, c. ) 0. 960 V 2. ) Δp ≥ 4. 22 × 10 -25 kgm/s 26