482dae288655821fd97ac1fe1394d9b8.ppt
- Количество слайдов: 12

Lecture 22: Random effects models BMTRY 701 Biostatistical Methods II

Independence Assumption § All of the regression assumptions we’ve discussed thus far assume independence § That is, patients (or other ‘units’) have outcomes that are unrelated § But what if they are? • • the same person is measured multiple times people from the same house are studied people treated in the same hospital are studied different tumors within the same patient are evaluated § In all of those examples, the independence assumption ‘falls apart’

How to deal with it? § Two main approaches: § Random effects model: • include a ‘random intercept’ to account for correlation • individuals who are ‘linked’ (i. e. , from same house, hospital, etc. ) receive the same intercept § Generalized estimating equations (GEE) • model the correlation as part of the regression • two part modeling: § mean model § covariance model

Nurse staffing in ICU example § Hospitals in MD from 1994 -1996, discharge data § All patients with abdominal aortic surgery (AAS) § Goal: evaluate the association between the nurse-to-patient ratio in the ICU for risk of medical and surgical complications after AAS. § Data: • patient outcomes (complications) • nurse: patient ratio § Issue: patients treated within the same hospital are likely to have correlated outcomes

Random effects modeling Standard logistic model Random effects logistic model

Adding in the random effect § Conditional on the random effect, the observations within a hospital are independence § Hence, independence is restored! § Even so, random effects are considered ‘nuisance parameters’ • we generally don’t care about them • they are necessary, but not interesting § Our primary interest is still in β 1
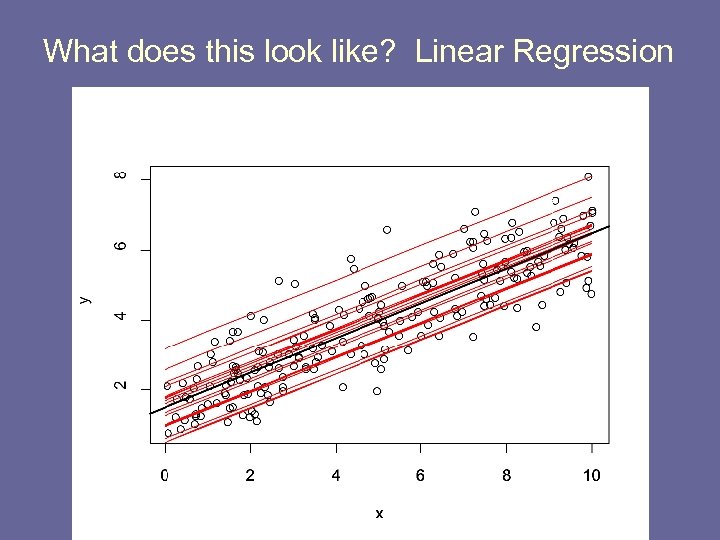
What does this look like? Linear Regression

Fitting Random Effects Models in R library(nlme) re. reg <- lme(y ~ x, random=~1|hospid) o. reg <- lm(y~x) bi <- re. reg$coefficients$random$hospid b 0 <- re. reg$coefficients$fixed[1] b 1 <- re. reg$coefficients$fixed[2] par(mfrow=c(1, 1)) plot(x, y) abline(o. reg) for(i in 1: 20) { lines(0: 10, b 0+b 1*(0: 10) + bi[i], col=2) } abline(o. reg, lwd=2)
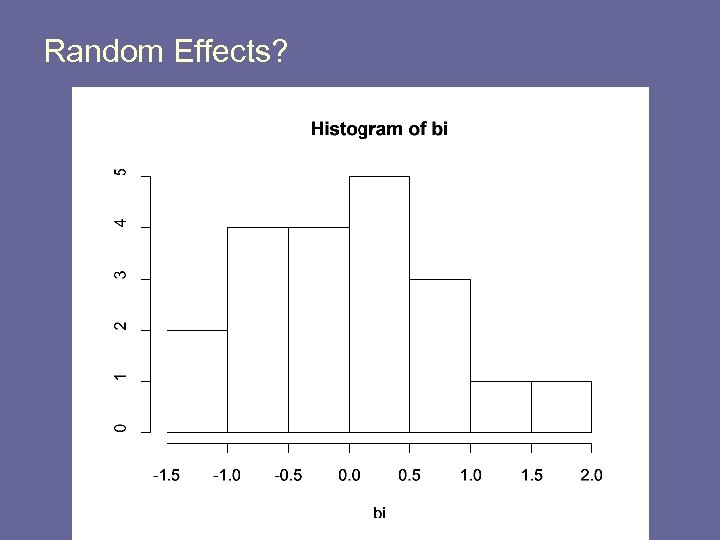
Random Effects?

Interpretation § Recall “nuisance” parameters § In most cases, we do not care about random intercepts § “Fixed” effects are interpreted in the same way as in a standard regression model

Stata § § xtreg: random effects linear regression xtlogit: random effects logistic regression xtpoisson: random effects poisson regression stcox, . . . shared(id): random effects Cox regression § Also, ‘cluster’ option in many regression commands in Stata

Applied example § http: //www. acponline. org/clinical_information/jou rnals_publications/ecp/sepoct 01/pronovost. htm
482dae288655821fd97ac1fe1394d9b8.ppt