8661c14cfeb1afc9d3ba148fb3d57af3.ppt
- Количество слайдов: 21

Lecture 21 State-Space Search vs. Constraint. Based Planning CSE 573 Artificial Intelligence I Henry Kautz Fall 2001 CSE 573 1

Road Map • Today • Plan graphs • Planning as state space search • Comparison of the two approaches CSE 573 2

Graphplan Planning as graph search (Blum & Furst 1995) Set new paradigm for planning Like SATPLAN. . . • Two phases: instantiation of propositional structure, followed by search Unlike SATPLAN. . . • Interleaves instantiation and pruning of plan graph • Employs specialized search engine Graphplan - better instantiation SATPLAN - better search CSE 573 3

Graph Pruning Graphplan instantiates in a forward direction, pruning unreachable nodes • conflicting actions are mutex • if all actions that add two facts are mutex, the facts are mutex • if the preconditions for an action are mutex, the action is unreachable! In logical terms: limited application of resolution where one clause is negative binary • given: P V Q, P V R V S V. . . • infer: Q V R V S V. . . CSE 573 4
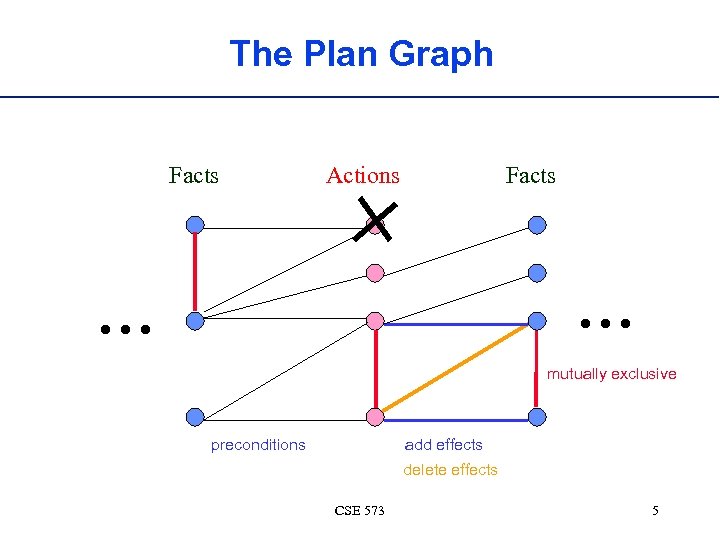
The Plan Graph Facts Actions Facts . . . mutually exclusive preconditions add effects delete effects CSE 573 5
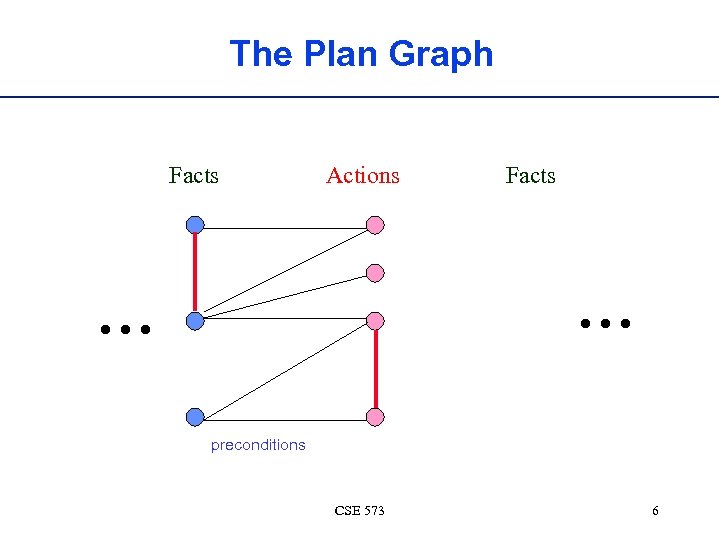
The Plan Graph Facts Actions Facts . . . preconditions CSE 573 6
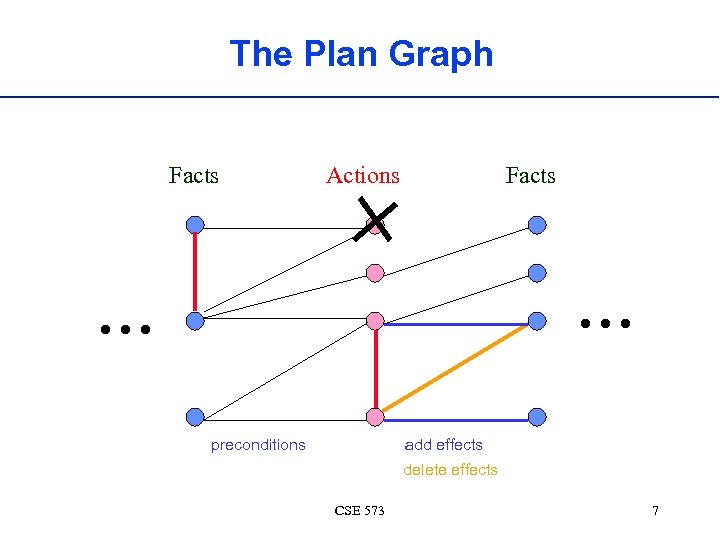
The Plan Graph Facts Actions Facts . . . preconditions add effects delete effects CSE 573 7
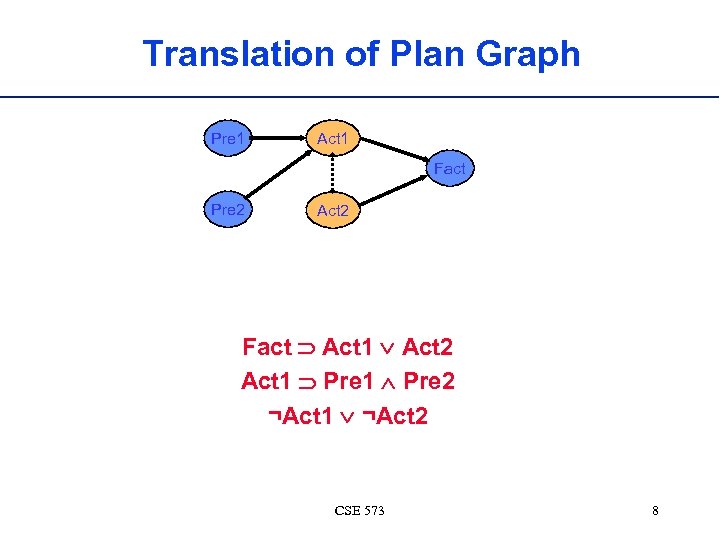
Translation of Plan Graph Pre 1 Act 1 Fact Pre 2 Act 2 Fact Act 1 Act 2 Act 1 Pre 2 ¬Act 1 ¬Act 2 CSE 573 8

Improved Encodings Translations of Logistics. a: STRIPS Axiom Schemas SAT (Medic system, Weld et. al 1997) • 3, 510 variables, 168 clauses • 24 hours to solve STRIPS Plan Graph SAT (Blackbox) • 2, 709 variables, 27, 522 clauses • 5 seconds to solve! CSE 573 9

Blackbox = Reachability + Satisfiability • Blackbox Planner (Kautz 1997) uses the first part of Graphplan (reachability analysis) to determine which propositions to instantiate • Then formula is generated (up to a bounded length K) and checked for SAT – can specify Walksat, various kinds of DP – current best: CHAFF (version DP) – can also run Graphplan on reachability graph for a few seconds to catch “easy” cases • If a solution found, then model is translated back to a parallel plan • Else max length K is incremented, and repeat CSE 573 10

Results: Logistics Planning Blackbox Graphplan rocket. b 5 sec 55 sec logistics. a 5 sec 31 minutes logistics. b 7 sec 13 minutes logistics. c 9 sec > 24 hours logistics. d 28 sec > 24 hours CSE 573 11

How Well Does it Work? 1992 – first incarnation of SATPLAN (Kautz & Selman), competitive with other planners (UCPOP) at the time 1995 – Graphplan (Blum & Furst) best planning algorithm – Constraint-satisfaction style solver, but no explicit translation to SAT – Blew everything previous out of the water! 1996 – SATPLAN with new SAT solvers (walksat+new local search heuristics, satz-rand, etc. ) – competitive with Graphplan – sometimes much faster – but requires hand-written axioms 1998 – Debut of Blackbox – Generates axioms automatically from STRIPS operators – Beats Graphplan when size & cost of generating formula small compared to graph search cost – Some domains kill it by blowing up size of formula: Blocks World, “Gripper” – Overall “winners” at AIP-98 competition were all constraint -based approaches (variants of SATPLAN and Graphplan) CSE 573 12

AIPS-2000 Another planning competition at the AI and Planning Systems Conference 2000 provided a big surprise: • Fastest planners were all based on A* search! • Heuristics derived automatically from STRIPS encoding Issues: • How to derive a search heuristic • How does A* really compare with constraintbased planning (Graphplan / SATPLAN / Blackbox)? CSE 573 13

Planning as A* Search Simple formulation: • State = node in search tree • Action = arc in search tree • Distance to goal = number of actions in plan • Note: purely sequential plans (no parallelism) Search heuristic: estimate of distance to goal • How to estimate? Ideas? CSE 573 14

Search Heuristics 1. Count number of false goal propositions in current state Admissible? 2. Delete all preconditions from actions, solve easy relaxed problem, use length Admissible? 3. Delete negative effects from actions, solve easier relaxed problem, use length Admissible? CSE 573 15

AIPS-2000 Planning Competition Fast-Forward (FF) • Joerg Hoffmann & Bernhard Nebel (Albert-Ludwigs-University Freiburg, Germany) • “Delete negative effects” heuristic • Competed in fully automated track of the 2 nd International Planning Systems Competition (AIPS 2000 conference in Breckenridge, CO) – Granted ``Group A distinguished performance Planning System'‘ – Schindler Award for the best performing planning system in the Miconic 10 Elevator domain AIPS 2002 – Toulouse, France Now, don’t you wish you were doing research on planning? CSE 573 16
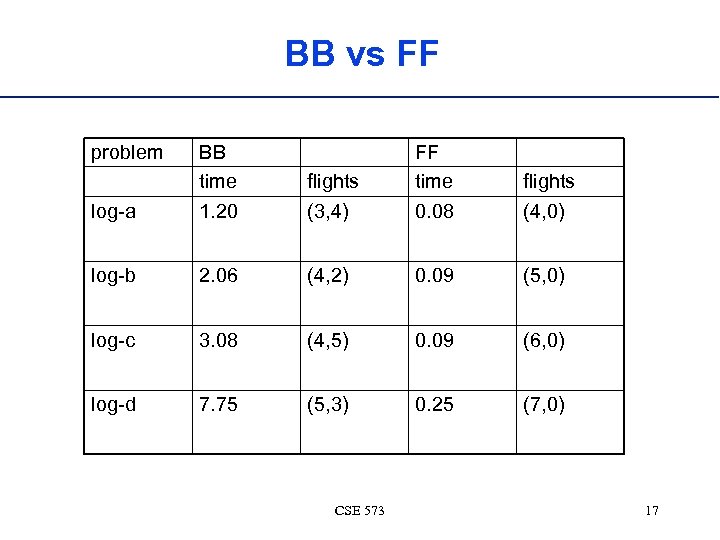
BB vs FF problem log-a BB time 1. 20 flights (3, 4) FF time 0. 08 flights (4, 0) log-b 2. 06 (4, 2) 0. 09 (5, 0) log-c 3. 08 (4, 5) 0. 09 (6, 0) log-d 7. 75 (5, 3) 0. 25 (7, 0) CSE 573 17

Hardness of Planning • FF (and other state-space planners) find solutions with unbalanced use of airplanes – little opportunities for post-facto parallelization • Logistics domain is actually polytime solvable if parallel plan length not considered! • NP-hard to find a solution with minimum parallel length Huang, Kautz, Selman 2002 – modify STRIPS operators to force solutions to be ones that can be parallelized! CSE 573 18

Modified STRIPS Logistics (: action FLY-AIRPLANE : parameters (? airplane ? loc-from ? loc-to ? r) : precondition (and (AIRPLANE ? airplane) (AIRPORT ? loc-from) (AIRPORT ? loc-to) (at ? airplane ? loc-from) (can_use ? airplane ? r) (resource ? r)) : effect (and (not (at ? airplane ? loc-from)) (not (resource ? r)) (at ? airplane ? loc-to))) ) CSE 573 (: init (at package bos-po). . . (resource r 1) (resource r 2) (resource r 3) (resource r 4) (can_use airplane 1 r 1) (can_use airplane 1 r 2) (can_use airplane 2 r 3) (can_use airplane 2 r 4). . . ) (: goal (at package la-po). . . ) 19

BB vs FF (modified logistics) problem BB time 1. 71 FF time 0. 12 log-b (3, 1) 2. 37 1. 61 log-c (3, 2) 9. 96 > 4 hours log-d (3, 4) 155. 1 > 4 hours log-a (3, 2) CSE 573 20

Coming Up • Wednesday • Prob(Prob) = 100% • Ch 14 – Review of basic probability theory • Ch 15 – start on Bayesian networks • Change in schedule • Only one more homework (not two), distributed Nov 28 th CSE 573 21
8661c14cfeb1afc9d3ba148fb3d57af3.ppt