Lecture 21 Goals Chapter 15 v Understand

Lecture 21 Goals: • Chapter 15 v Understand pressure in liquids and gases v Use Archimedes’ principle to understand buoyancy v Understand the equation of continuity v Use an ideal-fluid model to study fluid flow. v Investigate the elastic deformation of solids and liquids • Assignment v HW 9, Due Wednesday, Apr. 8 th v Thursday: Read all of Chapter 16 Physics 207: Lecture 21, Pg 1

Pressure vs. Depth Incompressible Fluids (liquids) l In many fluids the bulk modulus is such that we can treat the density as a constant independent of pressure: An incompressible fluid l For an incompressible fluid, the density is the same everywhere, but the pressure is NOT! l p(y) = p 0 - y g r = p 0 + d g r l Gauge pressure (subtract p 0, pressure 1 atm, i. e. car tires) F 2 = F 1+ m g = F 1+ r. Vg F 2 /A = F 1/A + r. Vg/A p 2 = p 1 - rg y Physics 207: Lecture 21, Pg 2

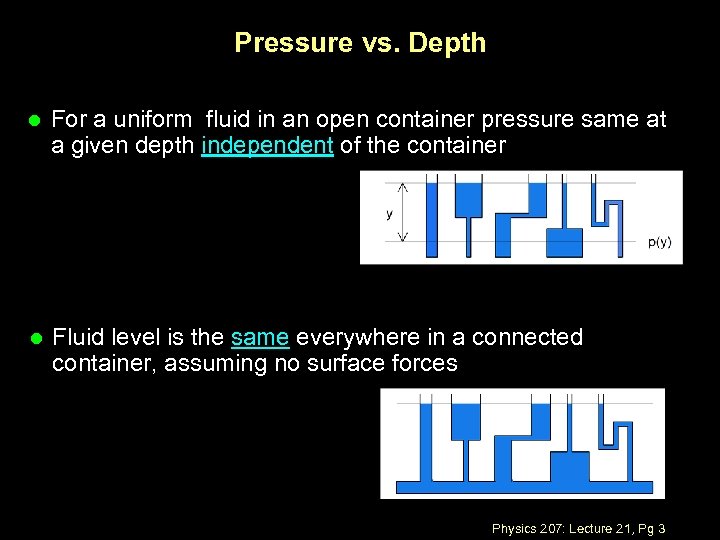Pressure vs. Depth l For a uniform fluid in an open container pressure same at a given depth independent of the container l Fluid level is the same everywhere in a connected container, assuming no surface forces Physics 207: Lecture 21, Pg 3

Pressure Measurements: Barometer l Invented by Torricelli l A long closed tube is filled with mercury and inverted in a dish of mercury v The closed end is nearly a vacuum l Measures atmospheric pressure as 1 atm = 0. 760 m (of Hg) Physics 207: Lecture 21, Pg 4

Exercise Pressure l What happens with two fluids? ? l Consider a U tube containing liquids of density r 1 and r 2 as shown: r 2 l At the red arrow the pressure must be the d. I r 1 y same on either side. r 1 x = r 2 (d 1+ y) v Compare the densities of the liquids: (A) r 1 < r 2 (B) r 1 = r 2 (C) r 1 > r 2 Physics 207: Lecture 21, Pg 5

Archimedes’ Principle: A Eureka Moment l Suppose we weigh an object in air (1) and in water (2). W 1 W 2? How do these weights compare? W 1 < W 2 l W 1 = W 2 W 1 > W 2 Buoyant force is equal to the weight of the fluid displaced Physics 207: Lecture 21, Pg 6

Archimedes’ Principle l Suppose we weigh an object in air (1) and in water (2). v How do these weights compare? W 1 < W 2 W 1 = W 2 v Why? Since the pressure at the bottom of the object is greater than that at the top of the object, the water exerts a net upward force, the buoyant force, on the object. W 1 > W 2 W 1 W 2? Physics 207: Lecture 21, Pg 8

Sink or Float? l The buoyant force is equal to the weight of the liquid that is displaced. l If the buoyant force is larger than the weight of the object, it will float; otherwise it will sink. y FB mg l We can calculate how much of a floating object will be submerged in the liquid: v Object is in equilibrium Physics 207: Lecture 21, Pg 9

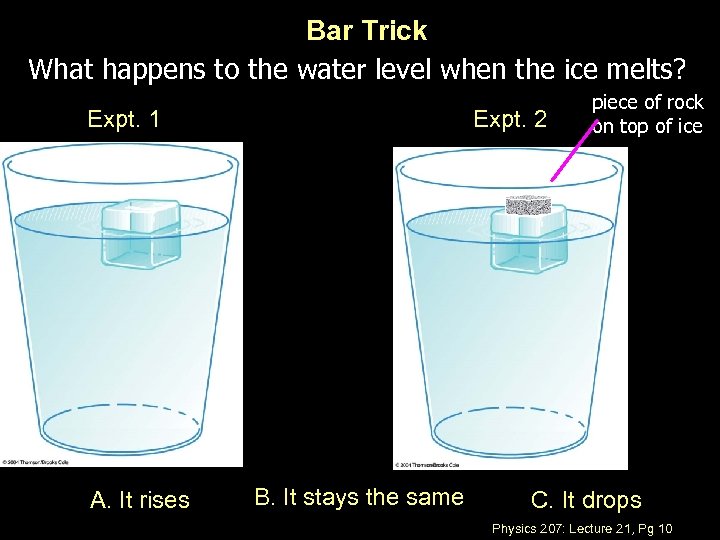Bar Trick What happens to the water level when the ice melts? Expt. 1 A. It rises Expt. 2 B. It stays the same piece of rock on top of ice C. It drops Physics 207: Lecture 21, Pg 10

Exercise V 1 = V 2 = V 3 = V 4 = V 5 m 1 < m 2 < m 3 < m 4 < m 5 What is the final position of each block? Physics 207: Lecture 21, Pg 11

Exercise V 1 = V 2 = V 3 = V 4 = V 5 m 1 < m 2 < m 3 < m 4 < m 5 What is the final position of each block? Not this But this Physics 207: Lecture 21, Pg 12

Pascal’s Principle l So far we have discovered (using Newton’s Laws): v Pressure depends on depth: Dp = r g Dy l Pascal’s Principle addresses how a change in pressure is transmitted through a fluid. Any change in the pressure applied to an enclosed fluid is transmitted to every portion of the fluid and to the walls of the containing vessel. Physics 207: Lecture 21, Pg 18

Pascal’s Principle in action: Hydraulics, a force amplifier l Consider the system shown: v A downward force F 1 is applied to the piston of area A 1. v This force is transmitted through the liquid to create an upward force F 2. v Pascal’s Principle says that increased pressure from F 1 (F 1/A 1) is transmitted throughout the liquid. l F 2 > F 1 with conservation of energy Physics 207: Lecture 21, Pg 19

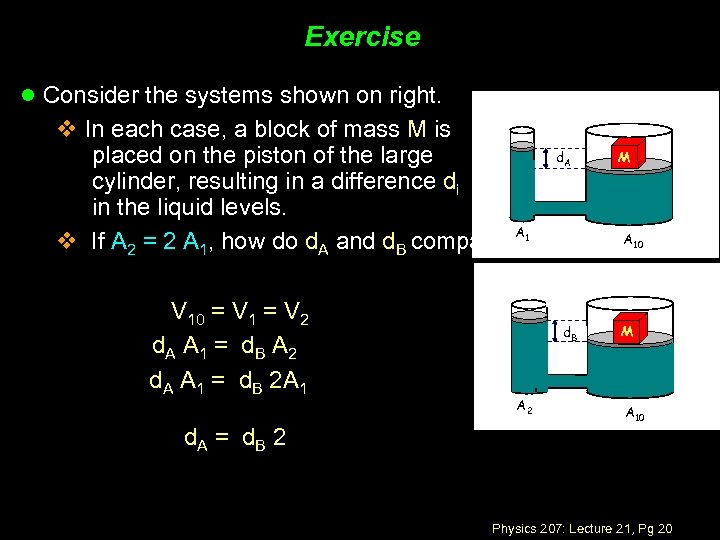Exercise l Consider the systems shown on right. v In each case, a block of mass M is placed on the piston of the large cylinder, resulting in a difference di in the liquid levels. A v If A 2 = 2 A 1, how do d. A and d. B compare? V 10 = V 1 = V 2 d. A A 1 = d B A 2 d. A A 1 = d. B 2 A 1 d. A = d B 2 d. A A 10 1 d. B A 2 M M A 10 Physics 207: Lecture 21, Pg 20

Fluids in Motion l To describe fluid motion, we need something that describes flow: v Velocity v l There are different kinds of fluid flow of varying complexity ç non-steady / steady ç compressible / incompressible ç rotational / irrotational ç viscous / ideal Physics 207: Lecture 21, Pg 22

Types of Fluid Flow l Laminar flow v Each particle of the fluid follows a smooth path v The paths of the different particles never cross each other v The path taken by the particles is called a streamline l Turbulent flow v An irregular flow characterized by small whirlpool like regions v Turbulent flow occurs when the particles go above some critical speed Physics 207: Lecture 21, Pg 23

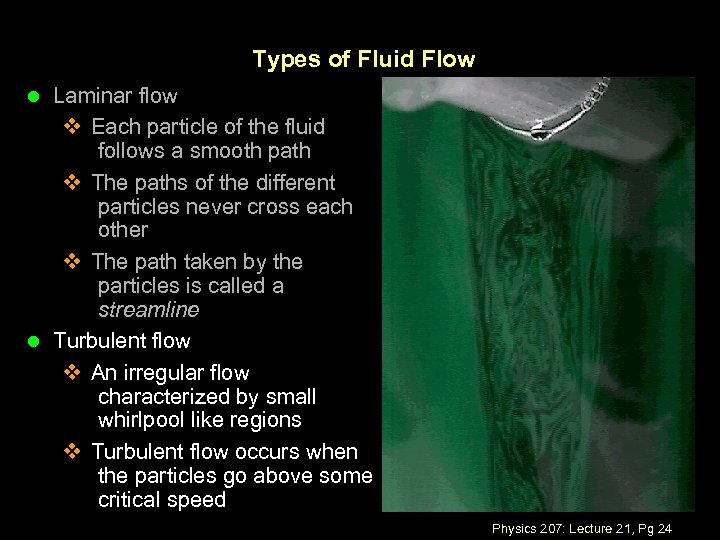Types of Fluid Flow l Laminar flow v Each particle of the fluid follows a smooth path v The paths of the different particles never cross each other v The path taken by the particles is called a streamline l Turbulent flow v An irregular flow characterized by small whirlpool like regions v Turbulent flow occurs when the particles go above some critical speed Physics 207: Lecture 21, Pg 24

Ideal Fluids l Streamlines do not meet or cross l Velocity vector is tangent to streamline l Volume of fluid follows a tube of flow bounded by streamlines A 2 A 1 v 2 l Streamline density is proportional to velocity l Flow obeys continuity equation Volume flow rate (m 3/s) Q = A·v is constant along flow tube. A 1 v 1 = A 2 v 2 Follows from mass conservation if flow is incompressible. Mass flow rate is just r Q (kg/s) Physics 207: Lecture 21, Pg 25

Exercise Continuity l A housing contractor saves some money by reducing the size of a pipe from 1” diameter to 1/2” diameter at some point in your house. v 1/2 v Assuming the water moving in the pipe is an ideal fluid, relative to its speed in the 1” diameter pipe, how fast is the water going in the 1/2” pipe? (A) 2 v 1 (B) 4 v 1 (C) 1/2 v 1 (D) 1/4 v 1 Physics 207: Lecture 21, Pg 26

Exercise Continuity (A) 2 v 1 (B) 4 v 1 (C) 1/2 v 1/2 (D) 1/4 v 1 l For equal volumes in equal times then ½ the diameter implies ¼ the area so the water has to flow four times as fast. l But if the water is moving 4 times as fast then it has 16 times as much kinetic energy. l Something must be doing work on the water (the pressure drops at the neck) and we recast the work as P DV = (F/A) (A Dx) = F Dx Physics 207: Lecture 21, Pg 27

Conservation of Energy for Ideal Fluid W = (P 1– P 2 ) DV and P 1 W = ½ Dm v 22 – ½ Dm v 12 P 2 = ½ (r DV) v 22 – ½ (r DV) v 12 (P 1– P 2 ) = ½ r v 22 – ½ r v 12 P 1+ ½ r v 12 = P 2+ ½ r v 22 = const. and with height variations: Bernoulli Equation P 1+ ½ r v 12 + r g y 1 = constant Physics 207: Lecture 21, Pg 29

Lecture 21 • Question to ponder: or float? Does heavy water (D 2 O) ice sink • Assignment v HW 9, due Wednesday, Apr. 8 th v Thursday: Read all of Chapter 16 Physics 207: Lecture 21, Pg 30