Lecture 21 Cross-classified and Multiple membership models

Lecture Contents • Cross classified models • AI example • Multiple membership models • Danish chickens example • More complex structures • ALSPAC educational example Thanks to Jon Rasbash for slides!

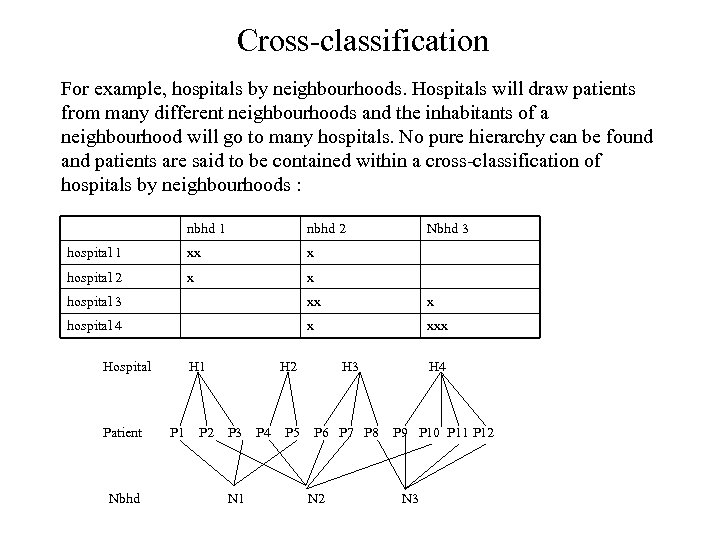
Cross-classification For example, hospitals by neighbourhoods. Hospitals will draw patients from many different neighbourhoods and the inhabitants of a neighbourhood will go to many hospitals. No pure hierarchy can be found and patients are said to be contained within a cross-classification of hospitals by neighbourhoods : nbhd 1 nbhd 2 hospital 1 xx x hospital 2 x Nbhd 3 x hospital 4 xx x xxx Hospital H 1 H 2 H 3 H 4 Patient P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 P 9 P 10 P 11 P 12 Nbhd N 1 N 2 N 3

Other examples of cross-classifications • pupils within primary schools by secondary schools. • patients within GPs by hospitals. • interviewees within interviewers by surveys. • repeated measures within raters by individual. (e. g. patients by nurses)

Notation With hierarchical models we use a subscript notation that has one subscript per level and nesting is implied reading from the left. For example, subscript pattern ijk denotes the i’th level 1 unit within the j’th level 2 unit within the k’th level 3 unit. If models become cross-classified we use the term classification instead of level. With notation that has one subscript per classification, that captures the relationship between classifications, notation can become very cumbersome. We propose an alternative notation introduced in Browne et al. (2001) that only has a single subscript no matter how many classifications are in the model.

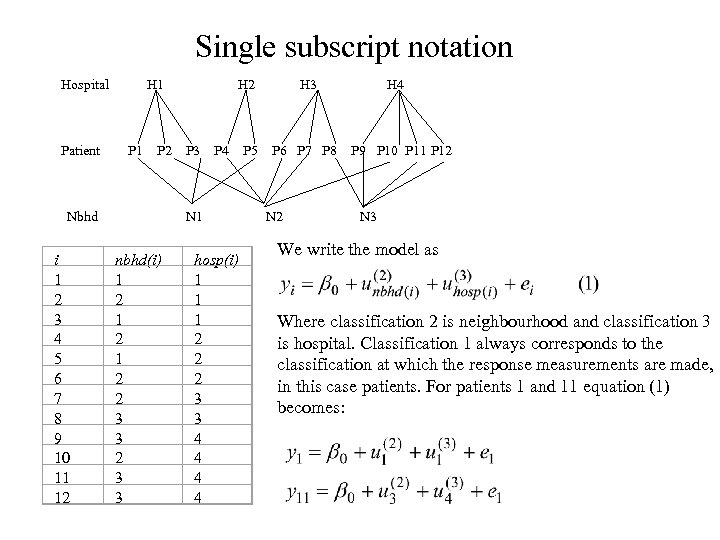
Single subscript notation Hospital H 1 H 2 H 3 H 4 Patient P 1 P 2 P 3 P 4 P 5 P 6 P 7 P 8 P 9 P 10 P 11 P 12 Nbhd N 1 N 2 N 3 i 1 2 3 4 5 6 7 8 9 10 11 12 nbhd(i) 1 2 1 2 2 3 3 hosp(i) 1 1 1 2 2 2 3 3 4 4 We write the model as Where classification 2 is neighbourhood and classification 3 is hospital. Classification 1 always corresponds to the classification at which the response measurements are made, in this case patients. For patients 1 and 11 equation (1) becomes:

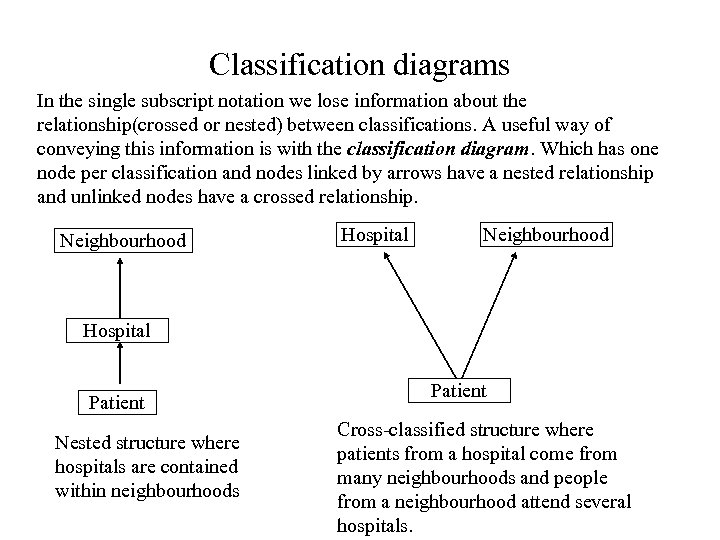
Classification diagrams In the single subscript notation we lose information about the relationship(crossed or nested) between classifications. A useful way of conveying this information is with the classification diagram. Which has one node per classification and nodes linked by arrows have a nested relationship and unlinked nodes have a crossed relationship. Neighbourhood Hospital Patient Nested structure where hospitals are contained within neighbourhoods Patient Cross-classified structure where patients from a hospital come from many neighbourhoods and people from a neighbourhood attend several hospitals.

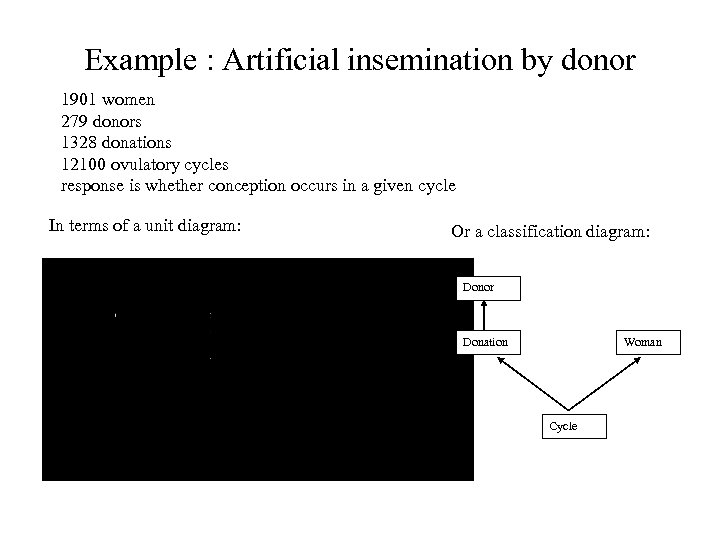
Example : Artificial insemination by donor 1901 women 279 donors 1328 donations 12100 ovulatory cycles response is whether conception occurs in a given cycle In terms of a unit diagram: Or a classification diagram: Donor Donation Woman Cycle

Model for artificial insemination data We can write the model as Results: Parameter Description intercept Estimate(se) -4. 04(2. 30) azoospermia * 0. 22(0. 11) semen quality 0. 19(0. 03) womens age>35 -0. 30(0. 14) sperm count 0. 20(0. 07) sperm motility 0. 02(0. 06) insemination to early -0. 72(0. 19) insemination to late -0. 27(0. 10) women variance 1. 02(0. 21) donation variance 0. 644(0. 21) donor variance 0. 338(0. 07)

Multiple membership models When level 1 units are members of more than one higher level unit we describe a model for such data as a multiple membership model. For example, • Pupils change schools/classes and each school/class has an effect on pupil outcomes. • Patients are seen by more than one nurse during the course of their treatment.

Notation Note that nurse(i) now indexes the set of nurses that treat patient i and w(2)i, j is a weighting factor relating patient i to nurse j. For example, with four patients and three nurses, we may have the following weights: n 1(j=1) n 2(j=2) n 3(j=3) p 1(i=1) 0. 5 0 0. 5 p 2(i=2) 1 0 0 p 3(i=3) 0 0. 5 p 4(i=4) 0. 5 0 Here patient 1 was seen by nurse 1 and 3 but not nurse 2 and so on. If we substitute the values of w(2)i, j , i and j. from the table into (1) we get the series of equations :

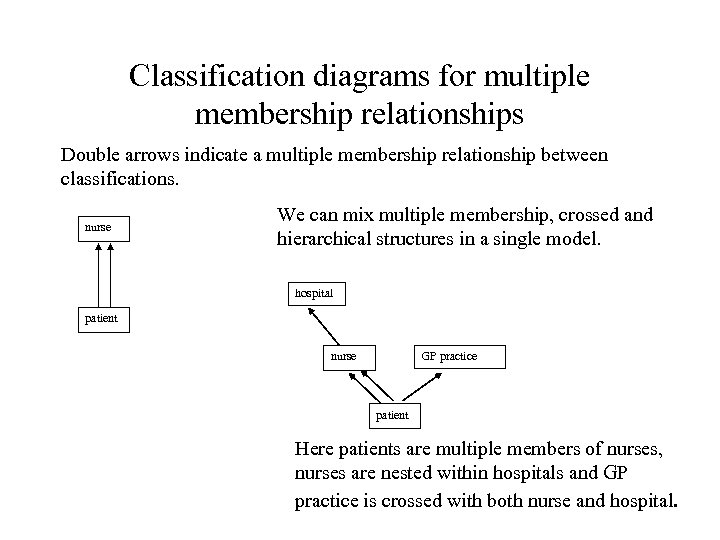
Classification diagrams for multiple membership relationships Double arrows indicate a multiple membership relationship between classifications. nurse We can mix multiple membership, crossed and hierarchical structures in a single model. hospital patient nurse GP practice patient Here patients are multiple members of nurses, nurses are nested within hospitals and GP practice is crossed with both nurse and hospital.

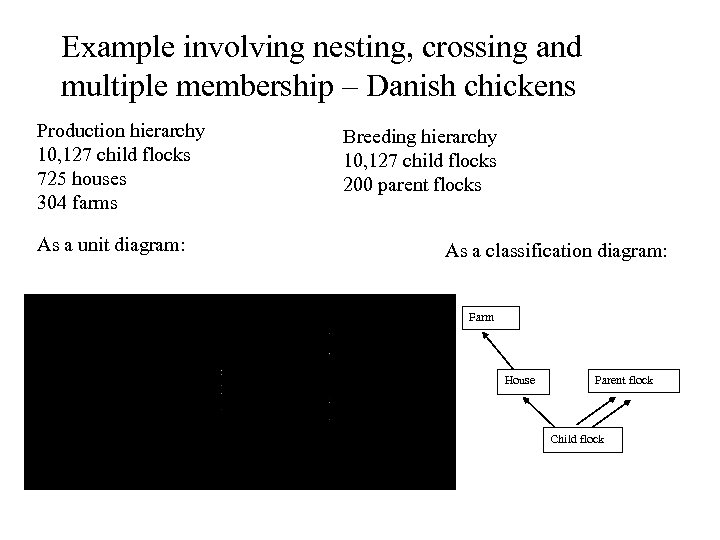
Example involving nesting, crossing and multiple membership – Danish chickens Production hierarchy Breeding hierarchy 10, 127 child flocks 10, 127 child flocks 725 houses 200 parent flocks 304 farms As a unit diagram: As a classification diagram: Farm House Parent flock Child flock

Model and results Results: Parameter Description Estimate(se) intercept -2. 322(0. 213) 1996 -1. 239(0. 162) 1997 -1. 165(0. 187) hatchery 2 -1. 733(0. 255) hatchery 3 -0. 211(0. 252) hatchery 4 -1. 062(0. 388) parent flock variance 0. 895(0. 179) house variance 0. 208(0. 108) farm variance 0. 927(0. 197)

ALSPAC data All the children born in the Avon area in 1990 followed up longitudinally. Many measurements made including educational attainment measures. Children span 3 school year cohorts(say 1994, 1995, 1996). Suppose we wish to model development of numeracy over the schooling period. We may have the following attainment measures on a child : m 1 m 2 m 3 m 4 m 5 m 6 m 7 m 8 primary school secondary school

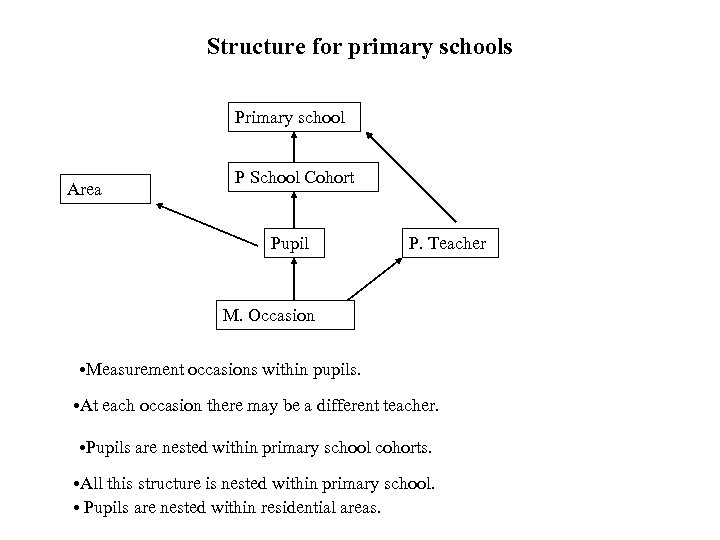
Structure for primary schools Primary school Area P School Cohort Pupil P. Teacher M. Occasion • Measurement occasions within pupils. • At each occasion there may be a different teacher. • Pupils are nested within primary school cohorts. • All this structure is nested within primary school. • Pupils are nested within residential areas.

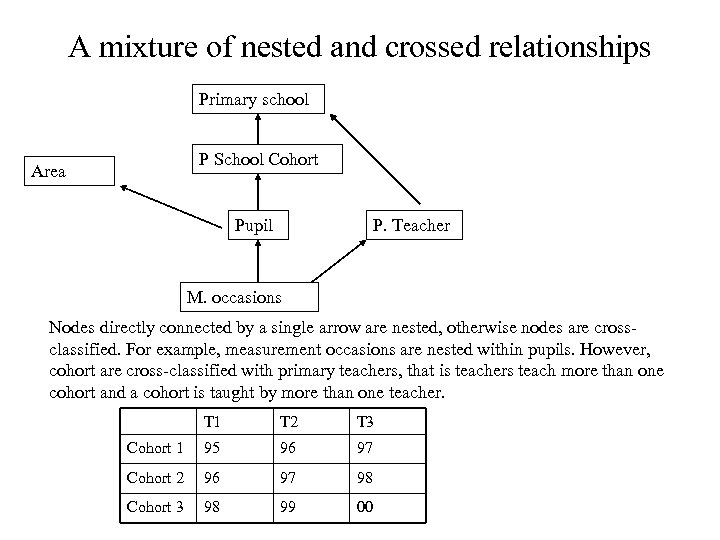
A mixture of nested and crossed relationships Primary school P School Cohort Area P. Teacher Pupil M. occasions Nodes directly connected by a single arrow are nested, otherwise nodes are crossclassified. For example, measurement occasions are nested within pupils. However, cohort are cross-classified with primary teachers, that is teachers teach more than one cohort and a cohort is taught by more than one teacher. T 1 T 2 T 3 Cohort 1 95 96 97 Cohort 2 96 97 98 Cohort 3 98 99 00

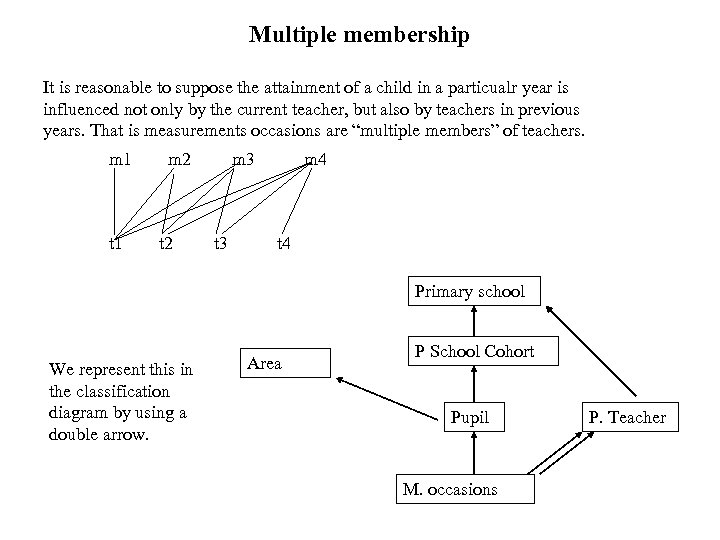
Multiple membership It is reasonable to suppose the attainment of a child in a particualr year is influenced not only by the current teacher, but also by teachers in previous years. That is measurements occasions are “multiple members” of teachers. m 1 m 2 m 3 m 4 t 1 t 2 t 3 t 4 Primary school We represent this in the classification diagram by using a double arrow. Area P School Cohort Pupil M. occasions P. Teacher

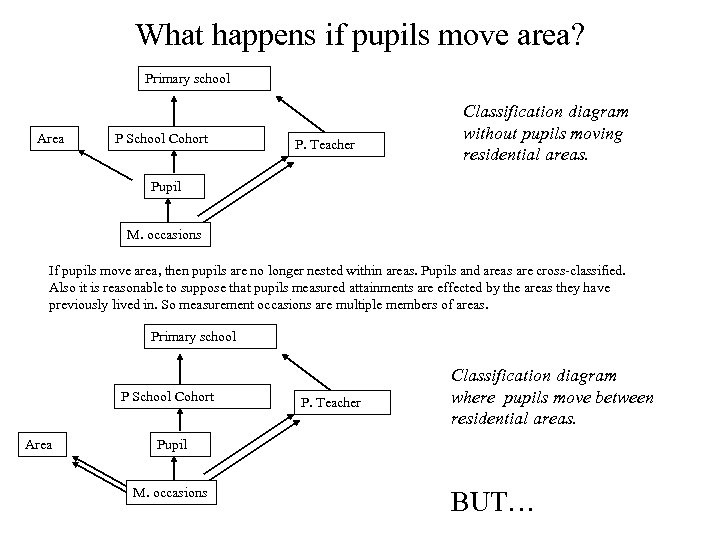
What happens if pupils move area? Primary school Area P School Cohort P. Teacher Classification diagram without pupils moving residential areas. Pupil M. occasions If pupils move area, then pupils are no longer nested within areas. Pupils and areas are cross-classified. Also it is reasonable to suppose that pupils measured attainments are effected by the areas they have previously lived in. So measurement occasions are multiple members of areas. Primary school P School Cohort Area P. Teacher Classification diagram where pupils move between residential areas. Pupil M. occasions BUT…

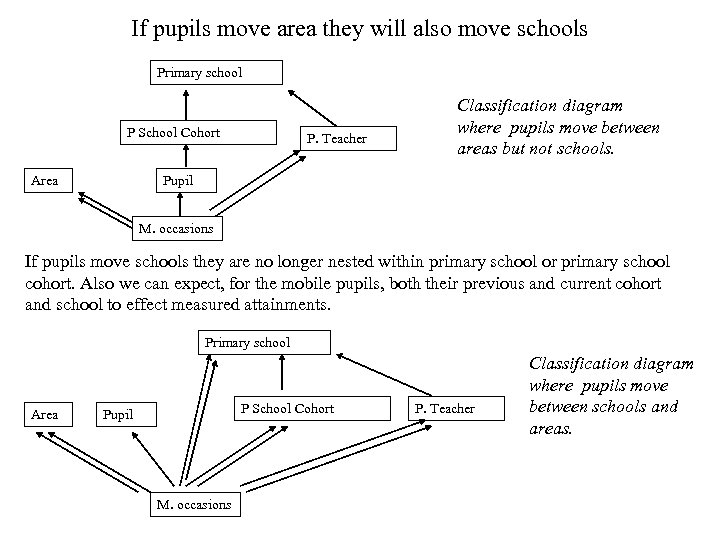
If pupils move area they will also move schools Primary school P School Cohort Area P. Teacher Classification diagram where pupils move between areas but not schools. Pupil M. occasions If pupils move schools they are no longer nested within primary school or primary school cohort. Also we can expect, for the mobile pupils, both their previous and current cohort and school to effect measured attainments. Primary school Area P School Cohort Pupil M. occasions P. Teacher Classification diagram where pupils move between schools and areas.

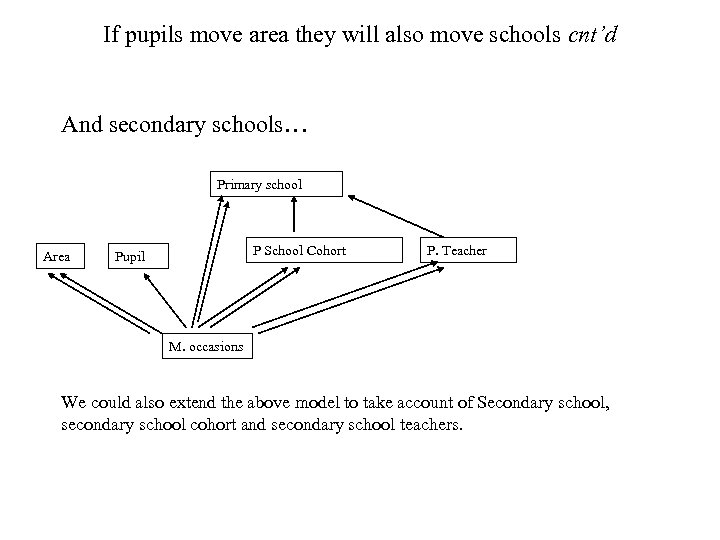
If pupils move area they will also move schools cnt’d And secondary schools… Primary school Area P School Cohort Pupil P. Teacher M. occasions We could also extend the above model to take account of Secondary school, secondary school cohort and secondary school teachers.

Other predictor variables Remember we are partitioning the variability in attainment over time between primary school, residential area, pupil, p. school cohort, teacher and occasion. We also have predictor variables for these classifications, eg pupil social class, teacher training, school budget and so on. We can introduce these predictor variables to see to what extent they explain the partitioned variability.

Information for the practicals • We have two MLwi. N practicals taken from chapters of Browne (2003). We firstly look at a cross-classified model for education data (primary schools and secondary schools. We secondly look at a multiple membership model for a (simulated) earnings dataset.