b0b8beacab30180969060ac6f439952b.ppt
- Количество слайдов: 38

Lecture 2 Properties of Galaxies Observational Properties Photometric Properties • • • magnitudes and luminosities colors (and color gradients) surface brightness (and photometric diameters) K-corrections brightness profiles Spectroscopic Properties Physical Properties the real shape mass, luminosity and diameter gas fraction stellar populations chemical composition Correlations of Structural Parameters the Faber-Jackson relation (E) the Tully-Fisher relation (S) Depto. de Astronomía (UGto) Astronomía Extragaláctica y Cosmología Observacional
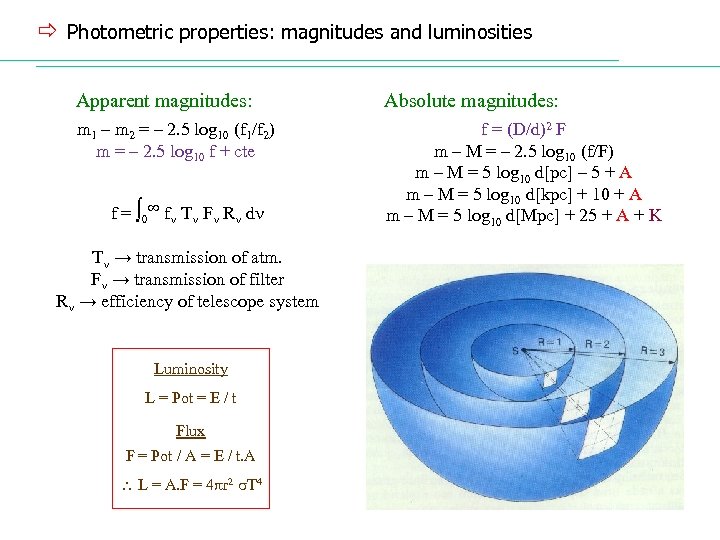
ð Photometric properties: magnitudes and luminosities Apparent magnitudes: Absolute magnitudes: m 1 – m 2 = – 2. 5 log 10 (f 1/f 2) m = – 2. 5 log 10 f + cte f = (D/d)2 F m – M = – 2. 5 log 10 (f/F) m – M = 5 log 10 d[pc] – 5 + A m – M = 5 log 10 d[kpc] + 10 + A m – M = 5 log 10 d[Mpc] + 25 + A + K f = ∫ 0∞ f T F R d T → transmission of atm. F → transmission of filter R → efficiency of telescope system Luminosity L = Pot = E / t Flux F = Pot / A = E / t. A L = A. F = 4 r 2 T 4
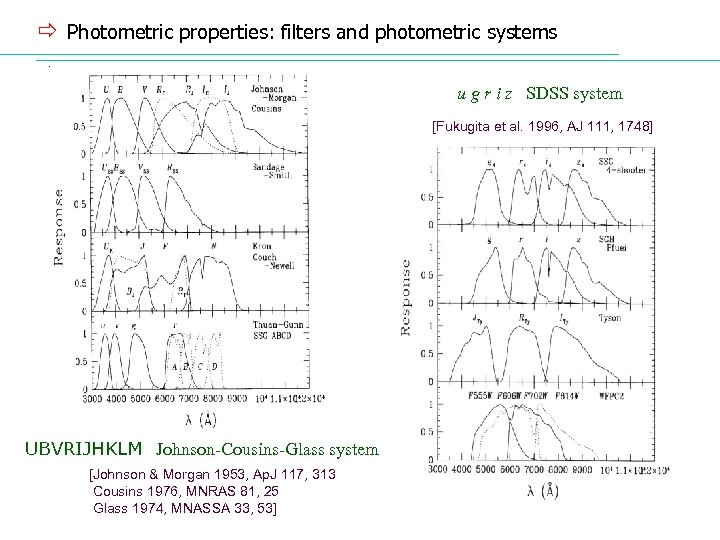
ð Photometric properties: filters and photometric systems u g r i z SDSS system [Fukugita et al. 1996, AJ 111, 1748] UBVRIJHKLM Johnson-Cousins-Glass system [Johnson & Morgan 1953, Ap. J 117, 313 Cousins 1976, MNRAS 81, 25 Glass 1974, MNASSA 33, 53]
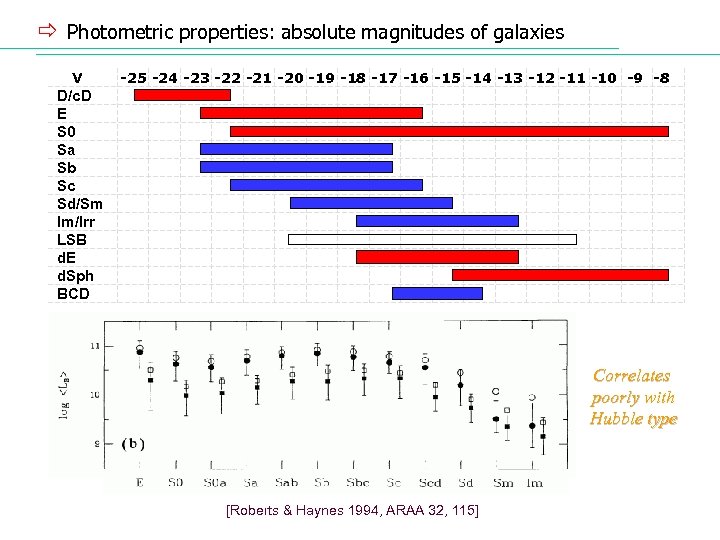
ð Photometric properties: absolute magnitudes of galaxies V -25 -24 -23 -22 -21 -20 -19 -18 -17 -16 -15 -14 -13 -12 -11 -10 -9 -8 D/c. D E S 0 Sa Sb Sc Sd/Sm Im/Irr LSB d. E d. Sph BCD Correlates poorly with Hubble type [Roberts & Haynes 1994, ARAA 32, 115]
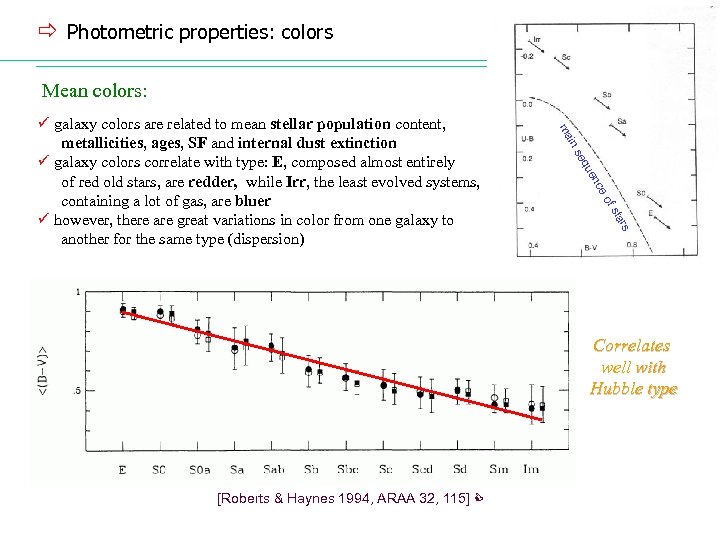
ð Photometric properties: colors Mean colors: in ma ce en qu se of rs sta ü galaxy colors are related to mean stellar population content, metallicities, ages, SF and internal dust extinction ü galaxy colors correlate with type: E, composed almost entirely of red old stars, are redder, while Irr, the least evolved systems, containing a lot of gas, are bluer ü however, there are great variations in color from one galaxy to another for the same type (dispersion) Correlates well with Hubble type [Roberts & Haynes 1994, ARAA 32, 115]
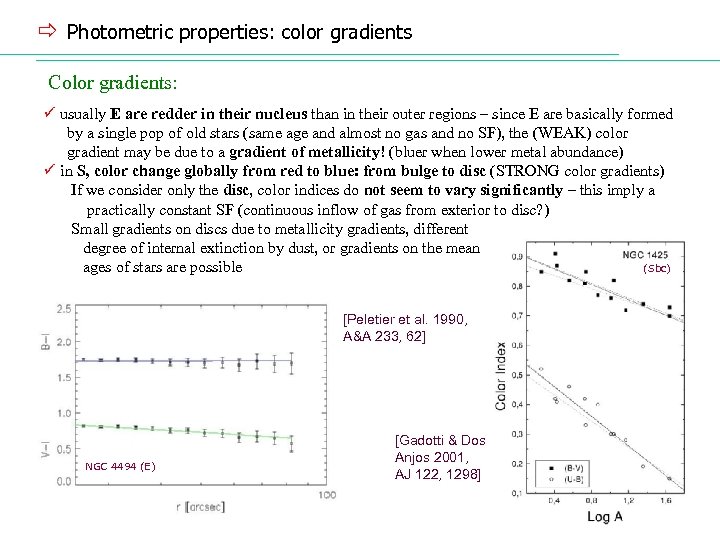
ð Photometric properties: color gradients Color gradients: ü usually E are redder in their nucleus than in their outer regions – since E are basically formed by a single pop of old stars (same age and almost no gas and no SF), the (WEAK) color gradient may be due to a gradient of metallicity! (bluer when lower metal abundance) ü in S, color change globally from red to blue: from bulge to disc (STRONG color gradients) If we consider only the disc, color indices do not seem to vary significantly – this imply a practically constant SF (continuous inflow of gas from exterior to disc? ) Small gradients on discs due to metallicity gradients, different degree of internal extinction by dust, or gradients on the mean (Sbc) ages of stars are possible [Peletier et al. 1990, A&A 233, 62] NGC 4494 (E) [Gadotti & Dos Anjos 2001, AJ 122, 1298]
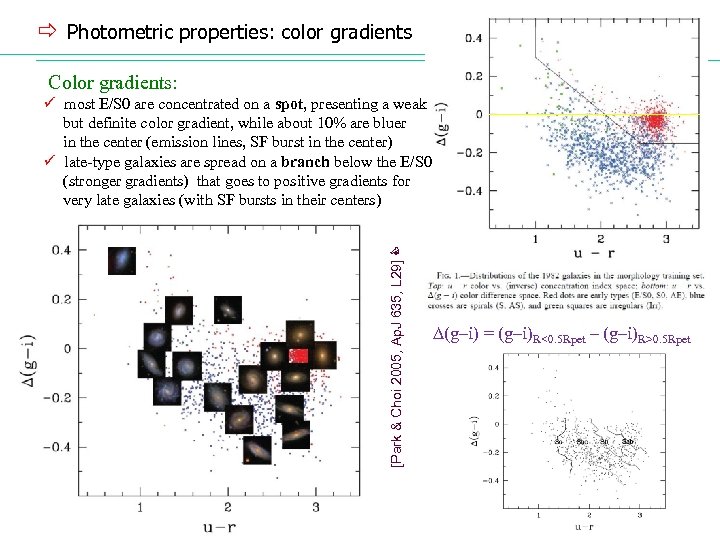
ð Photometric properties: color gradients Color gradients: [Park & Choi 2005, Ap. J 635, L 29] ü most E/S 0 are concentrated on a spot, presenting a weak but definite color gradient, while about 10% are bluer in the center (emission lines, SF burst in the center) ü late-type galaxies are spread on a branch below the E/S 0 (stronger gradients) that goes to positive gradients for very late galaxies (with SF bursts in their centers) (g–i) = (g–i)R<0. 5 Rpet – (g–i)R>0. 5 Rpet

ð Photometric properties: surface brightness Surface brightness: Σ = – 2. 5 log 10 (f/Ω) + cte ü to first approximation, the Σ of an extended object is independent of its distance: f falls of as 1/d 2 and also does the Ω in the same proportion ü is measured in mag arcsec-2 (or μm, where m is the magnitude band) Isophotes: ü curves that encircle areas of certain Σ (lines of equal Σ) Isophotal (or photometric) diameter: ü diameter at which some particular Σ level is reached (semimajor axis of the corresponding isophote) Holmberg radius → half diameter of galaxy at Σ = 26. 5 μpg de Vaucouleurs radius → half diameter of galaxy at Σ = 25 μB, corrected to face-on and of dust obscuration (called D 25) [de Vaucouleurs et al. 1991, 3 rd Reference Catalogue of Bright Galaxies]

ð Photometric properties: surface brightness Corrections to surface brightness measurements: ü sky brightness – at a good site, on a moonless night, the blank sky typically has a Σ 23 μB, due to: • air glow (photochemical processes in the upper atmosphere + Hg and Na lines radiation from street lamps of nearby cities) • zodiacal light (sunlight scattered off particulate matter in the SS) • MW background (diffuse light from faint and unresolved stars in the Galaxy) • extragalactic background (diffuse light from distant, faint, unresolved galaxies) μU 22. 0 μB 22. 7 μV 21. 8 μR 20. 9 μI 19. 9 ü seeing – the effect of seeing introduces an apparent core (PSF) into a surface brightness profile ü deprojection – correction of inclination in relation to the plane of sky (to face-on) ü obscuration by internal dust – for the case of late-type galaxies, dust can absorb or scatter their own light – the apparent lum. of a transparent galaxy is independent of its orientation to the LOS (stars emit light isotropically), but peak Σ increases as galaxy is tipped from face-on to edge-on (since at edge-on orientation the same lum. comes from a smaller area than at face-on) – but a galaxy filled with dust will appear to be less luminous when seen edge-on than face-on (light passes a longer column of ISM) – blue light is more strongly absorbed and scattered than red light [see Binney & Merrifield 1998, Galactic Astronomy, cap. 4. 2 and 4. 4]
ð Photometric properties: K-corrections K-correction (redshift dimming): [Pence 1976, Ap. J 203, 39; Hogg et al. 2002, astro-ph 0210394] ü since we do not cover the entire spectral range of galaxies we observe, to compare the measurements of galaxies at different z we must put them at a same reference frame (normally a standard measure at z = 0) ü so, the correction, called k-correction, depends on bands (filters) of observations, shapes of galaxies’s SEDs and z ü must be applied to magnitudes and Σ
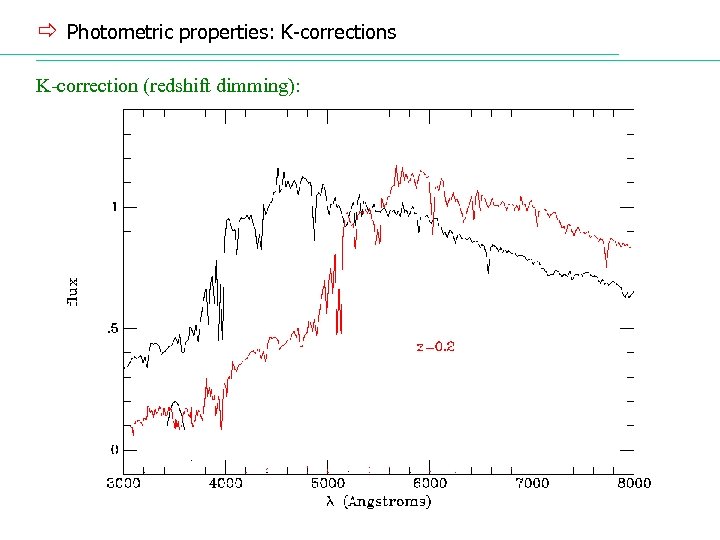
ð Photometric properties: K-corrections K-correction (redshift dimming):

ð Photometric properties: surface brightness profile for spheroids Radial profiles of Ellipticals: ü E have a pronounced maximum of Σ at their centre, and a rapid and uniform decrease with radial distance, following a quasi power law ü similar profile to bulges of S 0 s and spirals ü c. Ds have envelope and deviate in large r de Vaucouleurs’ profile [de Vaucouleurs 1948] log[Σ(r)/Σe] = – 3. 3307 [(r/Re)1/4 – 1] Σ(r) = Σe exp{– 7. 6692 [(r/Re)1/4 – 1]} Re = (ae be)1/2, is the radius containing half of total light (effective radius) Σe = Σ(Re) Σ 0 103. 33 Σe 2141 Σe Ltot = 7. 215 π Σe Re 2 (b/a) < Σ >e = 3. 6072 Σe Hubble’s profile [Hubble 1930] Σ(r) = Σ 0 (r/Rc + 1) – 2 Σ 0 = Σ(r=0) Rc is the core radius (where the surface brightness is Σ 0/2)
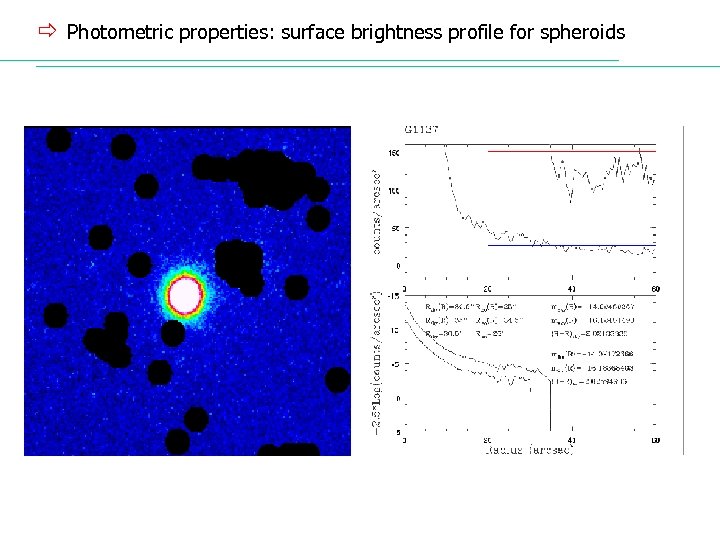
ð Photometric properties: surface brightness profile for spheroids
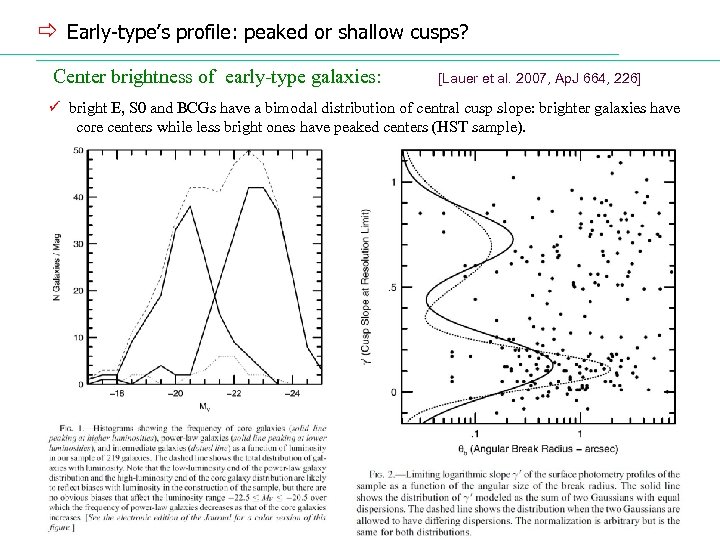
ð Early-type’s profile: peaked or shallow cusps? Center brightness of early-type galaxies: [Lauer et al. 2007, Ap. J 664, 226] ü bright E, S 0 and BCGs have a bimodal distribution of central cusp slope: brighter galaxies have core centers while less bright ones have peaked centers (HST sample).
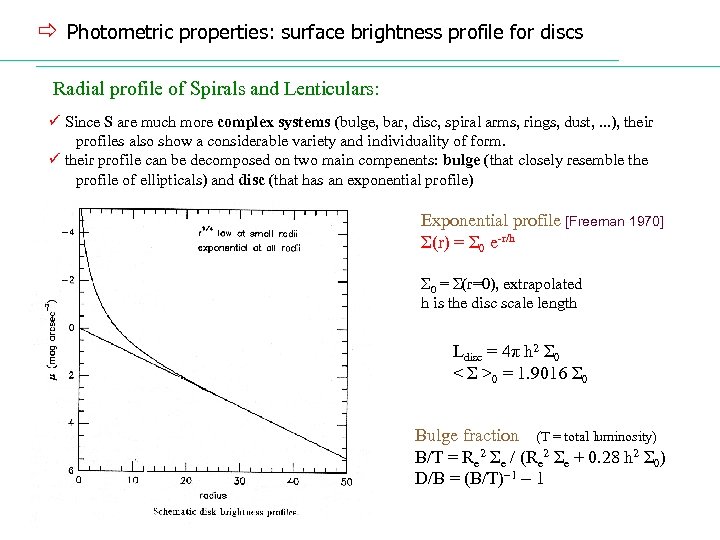
ð Photometric properties: surface brightness profile for discs Radial profile of Spirals and Lenticulars: ü Since S are much more complex systems (bulge, bar, disc, spiral arms, rings, dust, . . . ), their profiles also show a considerable variety and individuality of form. ü their profile can be decomposed on two main compenents: bulge (that closely resemble the profile of ellipticals) and disc (that has an exponential profile) Exponential profile [Freeman 1970] Σ(r) = Σ 0 e-r/h Σ 0 = Σ(r=0), extrapolated h is the disc scale length Ldisc = 4π h 2 Σ 0 < Σ >0 = 1. 9016 Σ 0 Bulge fraction (T = total luminosity) B/T = Re 2 Σe / (Re 2 Σe + 0. 28 h 2 Σ 0) D/B = (B/T) 1 1
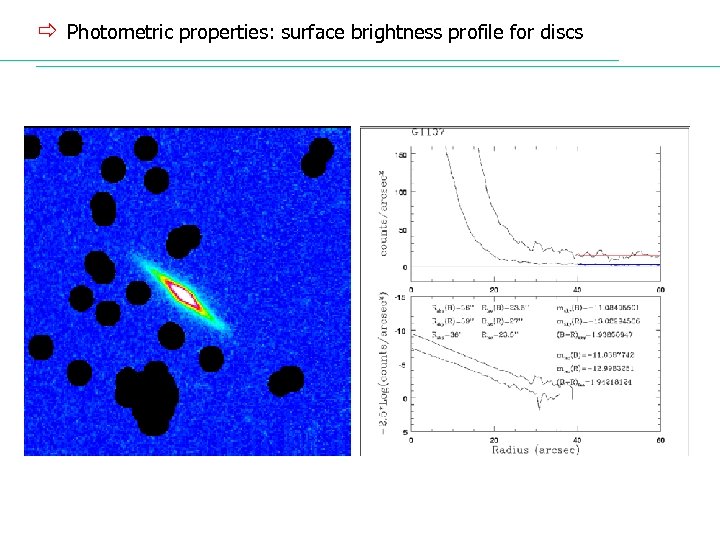
ð Photometric properties: surface brightness profile for discs
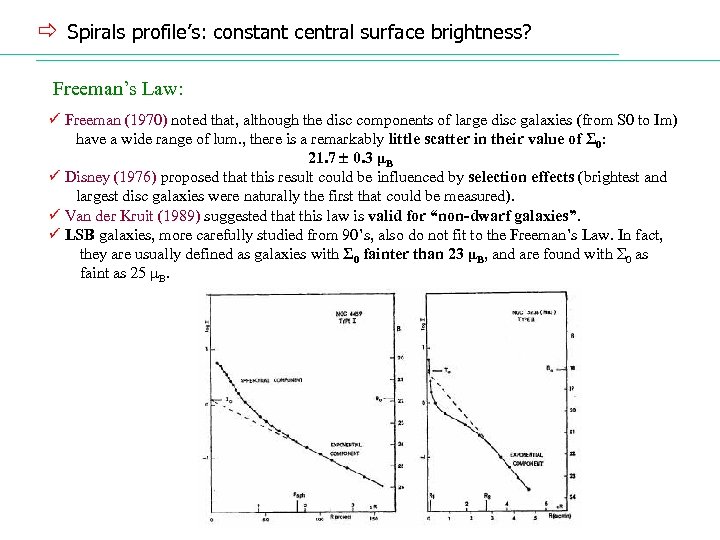
ð Spirals profile’s: constant central surface brightness? Freeman’s Law: ü Freeman (1970) noted that, although the disc components of large disc galaxies (from S 0 to Im) have a wide range of lum. , there is a remarkably little scatter in their value of Σ 0: 21. 7 0. 3 μB ü Disney (1976) proposed that this result could be influenced by selection effects (brightest and largest disc galaxies were naturally the first that could be measured). ü Van der Kruit (1989) suggested that this law is valid for “non-dwarf galaxies”. ü LSB galaxies, more carefully studied from 90’s, also do not fit to the Freeman’s Law. In fact, they are usually defined as galaxies with Σ 0 fainter than 23 μB, and are found with Σ 0 as faint as 25 μB.
![ð Photometric properties: general surface brightness profile Sersic’s generalized profile [Sersic 1968] Σ(r) = ð Photometric properties: general surface brightness profile Sersic’s generalized profile [Sersic 1968] Σ(r) =](https://present5.com/presentation/b0b8beacab30180969060ac6f439952b/image-18.jpg)
ð Photometric properties: general surface brightness profile Sersic’s generalized profile [Sersic 1968] Σ(r) = Σe exp{–bn [(r/Re)1/n – 1]} bn = 2 n – 0. 324 [Trujillo, Graham & Caon 2001] For a regular elliptical/bulge profile n = 4 b 4 = 7. 67 Σ(r) = Σe exp{– 7. 67 [(r/Re)1/4 – 1]} For an exponential disc profile n = 1 b 1 = 1. 68 Σ(r) = Σe exp{– 1. 68 [(r/Re) – 1]} = exp{1. 68} Σe exp{– 1. 68 r/Re} = 5. 36 Σe exp{–r/(Re/1. 68)} = Σ 0 exp{–r/h} Σ 0 = 5. 3567 Σe h = Re/1. 6783 [Pannella et al. 2006, Ap. J 639, L 1]

ð Spectroscopic properties Galaxy spectra: ü integrated spectra of galaxies give us information mainly on the stellar populations that compose the galaxy and on star formation (SF) ü classes of galaxy spectra are correlated with morphological classification ü population synthesis is the construction of a galaxy spectra from the combination of specific proportions of different types of stellar spectra. [Humason 1936] – first attempt to classify galaxy spectra: Absorption spectra (early-type): • stellar population: old stars • no recent SF (very low cold gas) • Balmer break (λ < 4000) – opacity of stellar photosphere increases fastly below this λ (presence of metals in different degrees of ionization) • absorption lines (produced on the atm. of cold red giants): Ca. II K (λ 3934), Ca. II H (λ 3969), G (λ 4304), Mgb (λ 5175), Ca+Fe (λ 5269), Na D (λ 5893), etc E (spectra close to G 3. 6) Sc (resembles F 8. 8) Emission spectra (late-type): • stellar population: rich in young OB stars • continuous SF (early S – decreases w/ time) (very gas rich) • high UV continuum (indicative of SF) • emission lines (produced by the gas, photoionized by energy from massive OB stars): OII (λ 3727), Hβ (λ 4861), OIII (λ 4959, λ 5007), Hα (λ 6563), NII (λ 6548, λ 6584), SII (λ 6717, λ 6731), etc
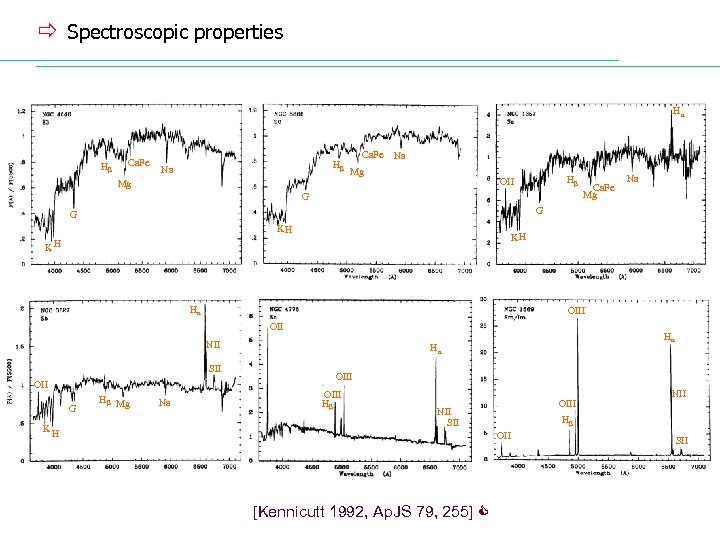
ð Spectroscopic properties H H Ca. Fe H Na Ca. Fe Na Mg H OII Mg G KH KH KH H OIII OII NII SII OII KH Na G G G Ca. Fe Mg H Mg Na H H OIII H OIII NII SII H OII [Kennicutt 1992, Ap. JS 79, 255] NII SII
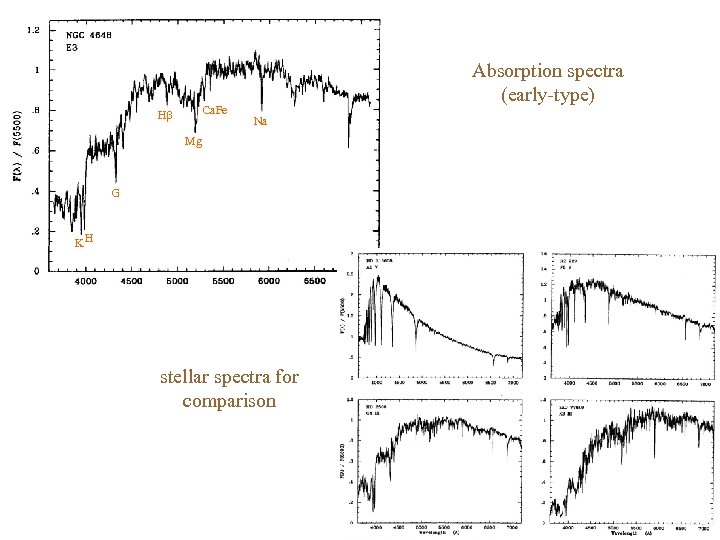
Ca. Fe H Absorption spectra (early-type) Na Mg G KH stellar spectra for comparison

OII H OIII H NII SII stellar spectra for comparison Emission spectra (late-type)
![ð Spectroscopic classification [Dressler et al. 1999, Ap. JS 122, 51] ð Spectroscopic classification [Dressler et al. 1999, Ap. JS 122, 51]](https://present5.com/presentation/b0b8beacab30180969060ac6f439952b/image-23.jpg)
ð Spectroscopic classification [Dressler et al. 1999, Ap. JS 122, 51]

ð Physical properties: the real shape of galaxies Elipticals ü ellipsoids spheroids a = b > c oblate a > b = c prolate triaxial a>b>c Spirals ü disks (flat oblate spheroids) inclination angle: i = arc cos (b/a) edge-on i = 90° face-on i = 0° plane of sky i a i cos(i) = b/a b
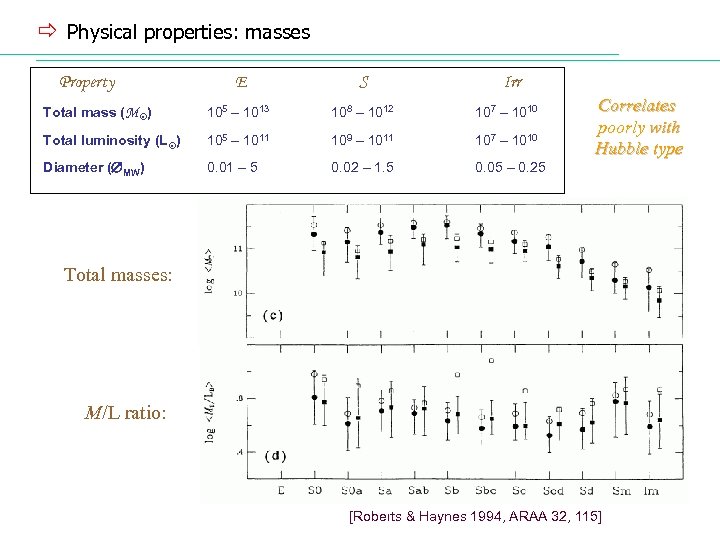
ð Physical properties: masses Property E S Irr Total mass (M ) 105 – 1013 108 – 1012 107 – 1010 Total luminosity (L ) 105 – 1011 109 – 1011 107 – 1010 Diameter ( MW) 0. 01 – 5 0. 02 – 1. 5 0. 05 – 0. 25 Correlates poorly with Hubble type Total masses: M/L ratio: [Roberts & Haynes 1994, ARAA 32, 115]
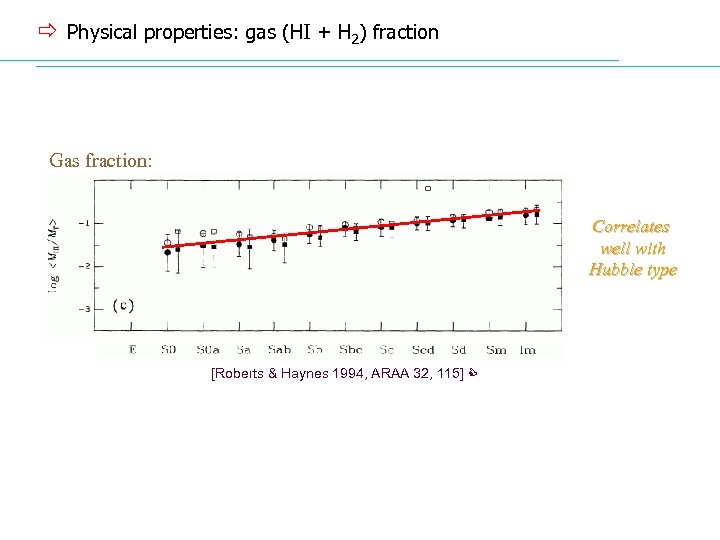
ð Physical properties: gas (HI + H 2) fraction Gas fraction: Correlates well with Hubble type [Roberts & Haynes 1994, ARAA 32, 115]
![ð Physical Properties: stellar content [Baade 1940] – introduced the idea of stellar populations ð Physical Properties: stellar content [Baade 1940] – introduced the idea of stellar populations](https://present5.com/presentation/b0b8beacab30180969060ac6f439952b/image-27.jpg)
ð Physical Properties: stellar content [Baade 1940] – introduced the idea of stellar populations (discs ellipticals/bulges) Population I: ü discs (particularly spiral arms) ü hot blue supergiants ü accompained by gas and dust ü Open Clusters ü young (CM diagram) ü higher metal abundances Population II: ü E, bulges, halos ü cool red giants ü gas and dust free ü Globular Clusters ü very old (CM diagram) ü deficient in metals Population III: ü zero metal
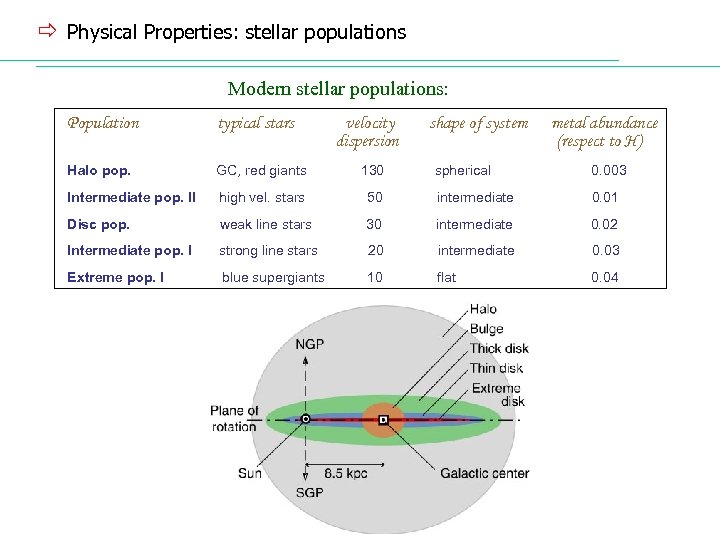
ð Physical Properties: stellar populations Modern stellar populations: Population typical stars velocity dispersion Halo pop. GC, red giants 130 Intermediate pop. II high vel. stars Disc pop. shape of system metal abundance (respect to H) spherical 0. 003 50 intermediate 0. 01 weak line stars 30 intermediate 0. 02 Intermediate pop. I strong line stars 20 intermediate 0. 03 Extreme pop. I blue supergiants 10 flat 0. 04
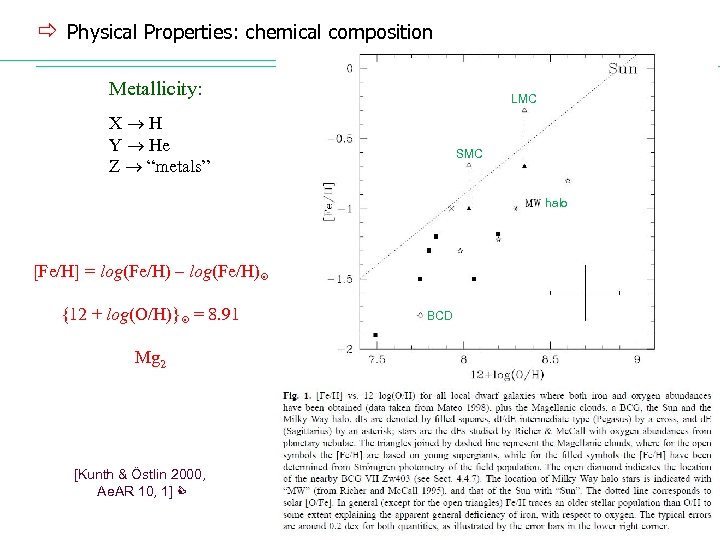
ð Physical Properties: chemical composition Metallicity: LMC X H Y He Z “metals” SMC halo [Fe/H] = log(Fe/H) – log(Fe/H) {12 + log(O/H)} = 8. 91 Mg 2 [Kunth & Östlin 2000, Ae. AR 10, 1] BCD
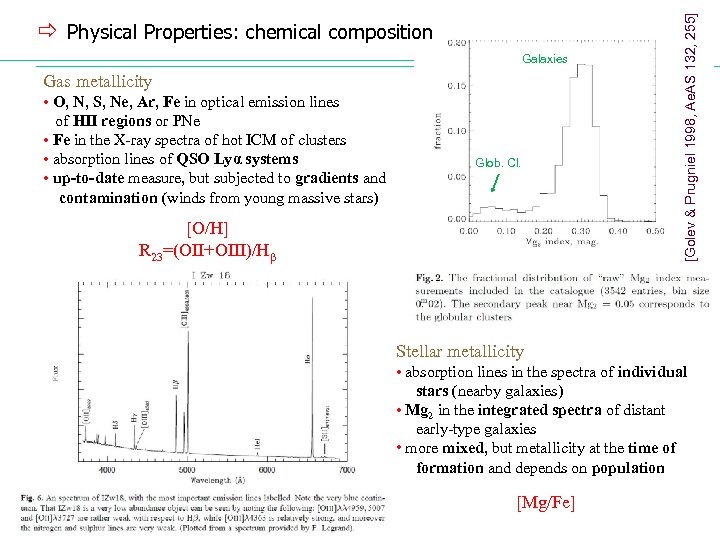
Galaxies Gas metallicity • O, N, S, Ne, Ar, Fe in optical emission lines of HII regions or PNe • Fe in the X-ray spectra of hot ICM of clusters • absorption lines of QSO Lyα systems • up-to-date measure, but subjected to gradients and contamination (winds from young massive stars) Glob. Cl. [O/H] R 23=(OII+OIII)/Hβ [Golev & Prugniel 1998, Ae. AS 132, 255] ð Physical Properties: chemical composition Stellar metallicity • absorption lines in the spectra of individual stars (nearby galaxies) • Mg 2 in the integrated spectra of distant early-type galaxies • more mixed, but metallicity at the time of formation and depends on population [Mg/Fe]
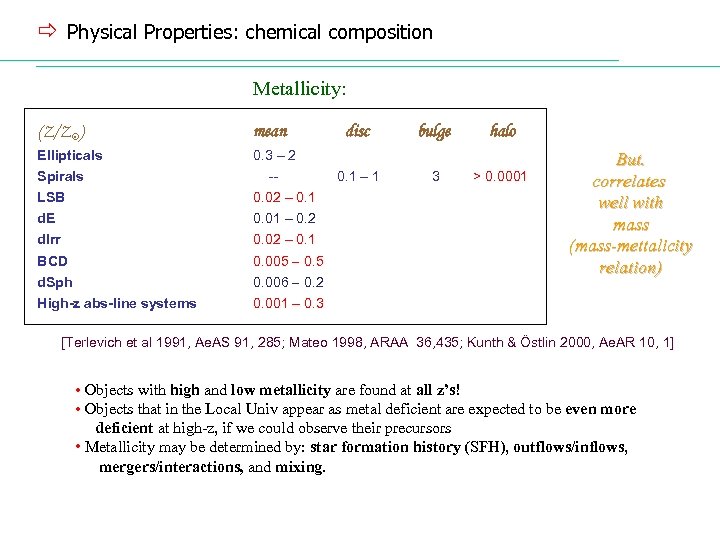
ð Physical Properties: chemical composition Metallicity: (Z/Z ) mean Ellipticals 0. 3 – 2 Spirals -- LSB 0. 02 – 0. 1 d. E 0. 01 – 0. 2 d. Irr 0. 02 – 0. 1 BCD 0. 005 0. 5 d. Sph 0. 006 0. 2 High-z abs-line systems disc 0. 1 – 1 bulge 3 halo > 0. 0001 But. correlates well with mass (mass-mettalicity relation) 0. 001 – 0. 3 [Terlevich et al 1991, Ae. AS 91, 285; Mateo 1998, ARAA 36, 435; Kunth & Östlin 2000, Ae. AR 10, 1] • Objects with high and low metallicity are found at all z’s! • Objects that in the Local Univ appear as metal deficient are expected to be even more deficient at high-z, if we could observe their precursors • Metallicity may be determined by: star formation history (SFH), outflows/inflows, mergers/interactions, and mixing.

ð Physical Properties: chemical composition Mass-Metallicity relation: • less massive galaxies are less able to retain the gas and stellar ejecta, loosing the freshly produced metals in the form of galactic outflows [Tremonti et al. 2004, Ap. J 613, 898] • high mass stars (that produce more and fastly metals) are preferencially produced in high SF epochs or sites (variable integrated stellar IMF) [Köppen et al. 2007, MNRAS 375, 673]
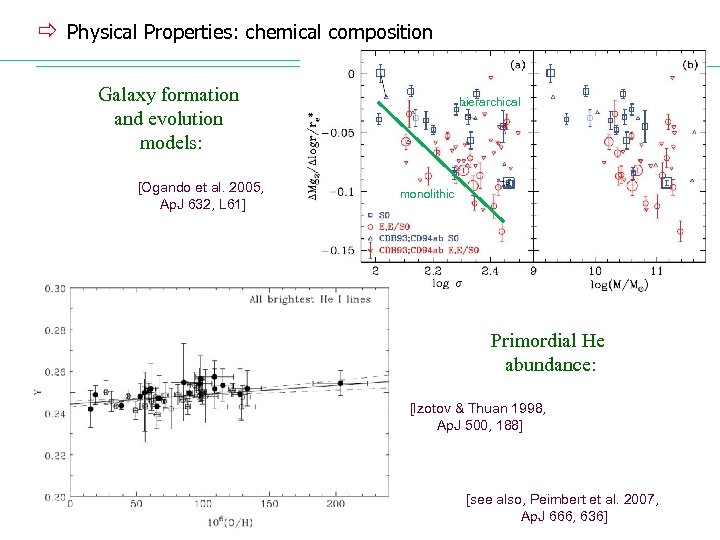
ð Physical Properties: chemical composition Galaxy formation and evolution models: [Ogando et al. 2005, Ap. J 632, L 61] hierarchical monolithic Primordial He abundance: [Izotov & Thuan 1998, Ap. J 500, 188] [see also, Peimbert et al. 2007, Ap. J 666, 636]
![ð Correlations of physical properties: the Faber-Jackson relation [Faber & Jackson 1976] – discovered, ð Correlations of physical properties: the Faber-Jackson relation [Faber & Jackson 1976] – discovered,](https://present5.com/presentation/b0b8beacab30180969060ac6f439952b/image-34.jpg)
ð Correlations of physical properties: the Faber-Jackson relation [Faber & Jackson 1976] – discovered, for E, a relation between the lum. (L) and the central stellar velocity dispersion (σ0): 4 L e σ0 [Djorgovski & Davies 1987 and Dressler et al. 1987] – introduced the concept of Fundamental Plane (L σ0 r) log Re = 0. 36 <Σe> + 1. 4 log σ0 Le σ08/3 Σe-3/5 [Dressler et al. 1987] – also proposed the Dn–σ relation (incorporating the dependende of both L and Σe into a new variable Dn) σ0 Dn 3/4 Dn → Σn = 20. 75 μB ü if σ0 can be measured for an E, its intrinsic L can be found by the relation, and hence, by measuring its flux, its distance can be found. [Σ = f (L, r)]
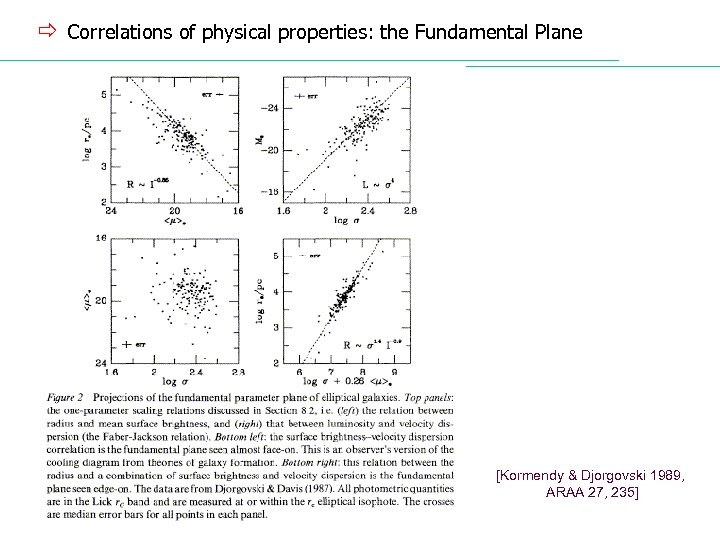
ð Correlations of physical properties: the Fundamental Plane [Kormendy & Djorgovski 1989, ARAA 27, 235]
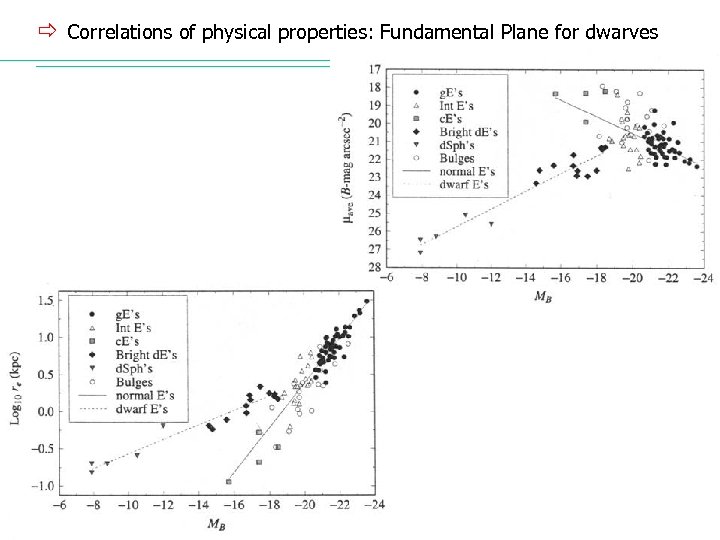
ð Correlations of physical properties: Fundamental Plane for dwarves
![ð Correlations of physical properties: the Tully-Fisher relation [Tully & Fisher 1977] – discovered, ð Correlations of physical properties: the Tully-Fisher relation [Tully & Fisher 1977] – discovered,](https://present5.com/presentation/b0b8beacab30180969060ac6f439952b/image-37.jpg)
ð Correlations of physical properties: the Tully-Fisher relation [Tully & Fisher 1977] – discovered, for S, a relation between the lum. (L) and the width of the 21 -cm HI line profile (that is related to the maximum rotation velocity – Doppler broadening). L Wα α = 2. 5 B [Aaronson, Huchra & Mould 1979] – in the IR, the Tully-Fisher relation is more tightly correlated [Aaronson & Mould 1983] – α = 3. 5 (B band) α = 4. 3 (H band) ü if W can be measured for an S, its intrinsic L can be found by the relation, and hence, by measuring its flux, its distance can be found.

ð References: Papers and books: Ø E. P. Hubble 1930, Ap. J 71, 231 Ø M. Humason 1936, Ap. J 83, 10 Ø W. Baade 1940, Ap. J 100, 137 Ø G. De Vaucouleurs 1948, Ann. Astrophys. 11, 247 Ø J. –L. Sersic 1968, “Atlas de Galaxias Australes” (Cordoba, Obs. Astronomico) Ø K. C. Freeman 1970, Ap. J 160, 811 Ø M. Disney 1976, Nature 263, 573 Ø S. M. Faber & R. E. Jackson 1976, Ap. J 204, 668 Ø B. Tully & J. R. Fisher 1977, A&A 54, 661 Ø M. Aaronson, J. Huchra & J. Mould 1979, Ap. J 229, 1 Ø M. Aaronson & J. Mould 1983, Ap. J 265, 1 Ø S. Djorgovski & M. Davis 1987, Ap. J 313, 59 Ø A. Dressler et al. 1987, Ap. J 313, 42 Ø P. C. van der Kruit 1989, In: “The Milky Way as a Galaxy”, eds. R. Buser & I. King Ø I. Trujillo et al. 2001, MNRAS 326, 869 Ø K. Rakos et al. 2003, Ap&SS, 284, 803 Ø J. Moustakas & R. Kennicutt 2006, Ap. J 651, 155
b0b8beacab30180969060ac6f439952b.ppt