Lecture 2 Crystallization Symmetry crystal growth theory

Lecture 2: Crystallization & Symmetry crystal growth theory symmetry operators space groups

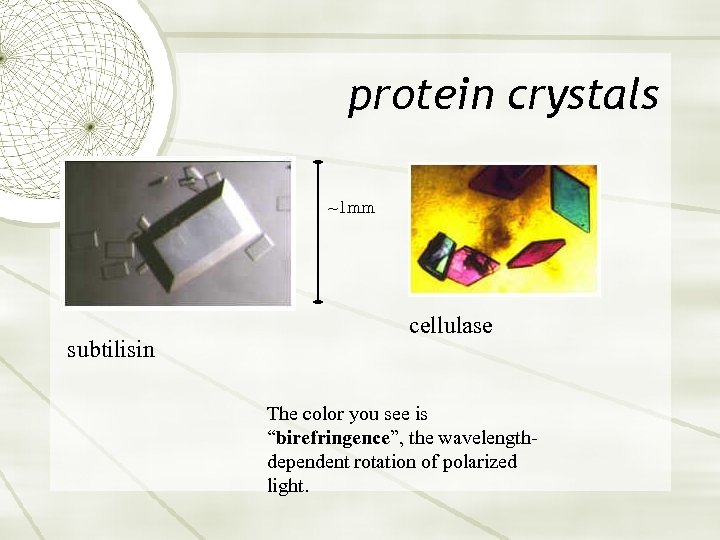protein crystals ~1 mm subtilisin cellulase The color you see is “birefringence”, the wavelengthdependent rotation of polarized light.

Crystallization robot High-throughput crystallography labs use pipeting robots to explore thousnds of “conditions”. Each condition is a formulation of the crystal drop and the reservoir solution. Conditions can have different: • protein concentration • p. H • precipitant, precipitant concentration • detergents • organic co-solvents • metal ions • ligands • concentration gradient

Protein crystal growth protein concentration Arrows indicate different diffusion experients. A, B, D, F, G. Vapor diffusion. E. Bulk C. Microdialysis precipitant concentration blue line = saturation of protein red line = supersaturation limit L=liquid S=solid m=metastable state (supersaturated) Crystal growth occurs between these two limits. Above the supersaturation limit, proteins form only disordered precipitate.

vapor diffusion setup a Linbro plate Volatiles (i. e. water) evaporate from one surface and condence on the other. Drop has higher water concentration than reservoir, so drop slowly evaporates.

Other ways to supersaturate slowly Sitting drops Microdialysis Gel filtration

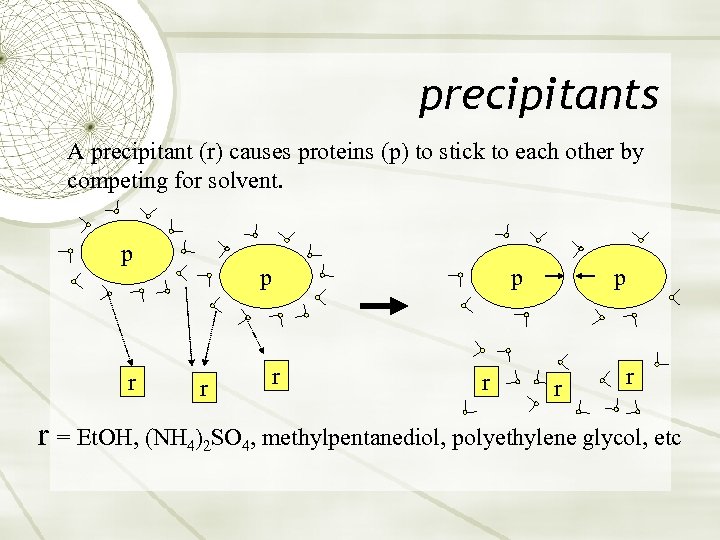precipitants A precipitant (r) causes proteins (p) to stick to each other by competing for solvent. p r p r r r = Et. OH, (NH 4)2 SO 4, methylpentanediol, polyethylene glycol, etc

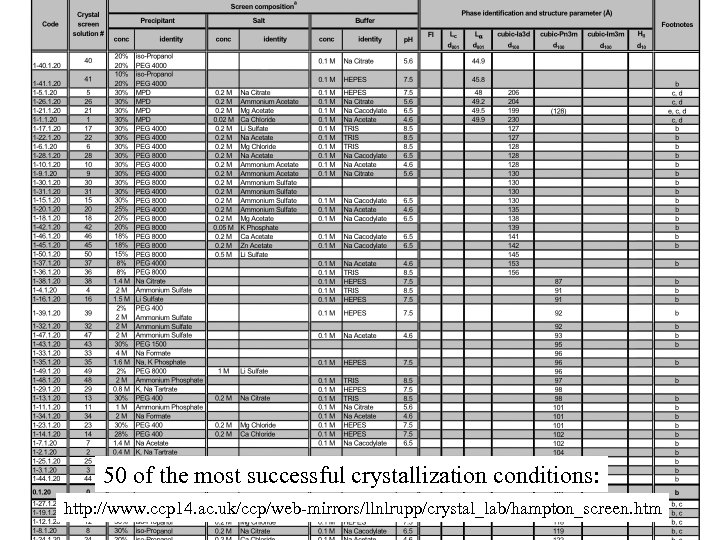50 of the most successful crystallization conditions: http: //www. ccp 14. ac. uk/ccp/web-mirrors/llnlrupp/crystal_lab/hampton_screen. htm

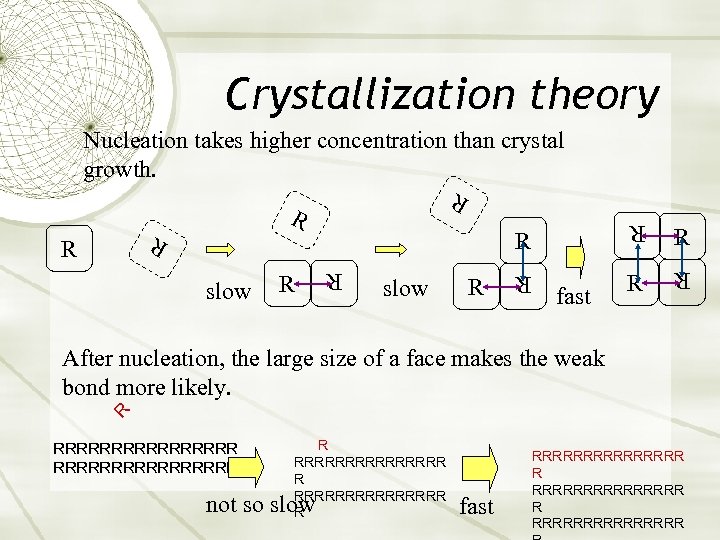Crystallization theory Nucleation takes higher concentration than crystal growth. R R R slow R R fast R R R After nucleation, the large size of a face makes the weak bond more likely. RRRRRRRRRRRRRRRR R not so slow fast RRRRRRRRRRRRRRR R RRRRRRRR

Periodic Bond Chain theory Bonds A, B are stronger than P, Q. Dimensions of crystal at equilibrium are proportional. More on Periodic Bond Chain theory: http: //www. che. utoledo. edu/nadarajah/webpages/PBC. htm

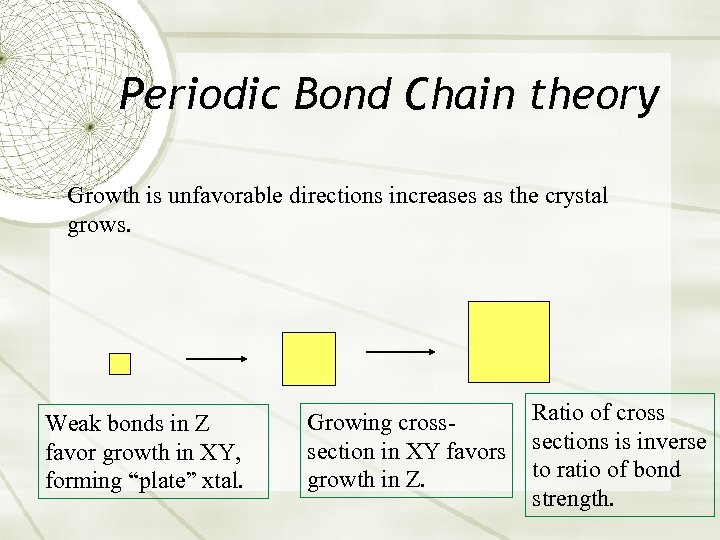Periodic Bond Chain theory Growth is unfavorable directions increases as the crystal grows. Weak bonds in Z favor growth in XY, forming “plate” xtal. Growing crosssection in XY favors growth in Z. Ratio of cross sections is inverse to ratio of bond strength.

diffusion depletion Crystal growth depletes the surrounding solution of protein, while concentrating impurities. Local depletion. . . prevents nucleations close to a growing crystal. . . slows and eventually stops crystal growth . . . concentrates impurities on the surface of the crystal. . . causes convection currents. Cobalt impurities in Si. O 2 (amethyst) are concentrated in the part of the crystal that formed last (the tip).

Better crystals in micro gravity? Higher concentration of protein = higher density Differences in densty cause convection currents, which might cause crystal defects. Microgravity eliminates convection currents. More at: http: //science. nasa. gov/ssl/msad/pcg/

mounting crystals Thin-walled glass capillaries (<1 mm in diameter) are filled with “mother liquor”(the fluid in which the crystal was grown) and a crystal is carefully dropped in. The mother liquor is removed using filter paper cut to fine strips. The crystal sticks to the glass, immobilized. The xtal remains in vapor diffusion contact with the mother liquor. If not it will dryout and crack. Protein crystals are extremely fragile!!! They may break upon sudden contact with a solid object. Tiny pipets are used to pull crystals from drops.

Crystal mounting If not freezing Xtal is mounted in a thin-walled glass capillary tube If freezing (preferred) Xtal is mounted on a thin film of water in a wire loop. The loop is fixed to a metal or glass rod. Mounted xtal is attached to a goniometer head for precise adjustment. Low-melting hard wax is used to ‘glue’ the rod or capillary here. Small wrenches fit here, here and here. wax Must freeze immediately or film will dry out. ! Crystal must be kept at proper humidity and temperature!! Very fragile! eucentric goniometer head (made by Nonius)

Why freeze? Essentially eliminates X-ray damage to crystal. Crystals do not decay during data collection. Why not? wire-loop crystal catcher Cryo equipment is expensive. Ice crystals may form if freezing is not done properly, ruining data.

Crystals must be flash frozen. . . to prevent glass->ice transition Water must be frozen to < – 70°C very fast to prevent the formation of hexagonal ice. Water glass forms. How? Crystals, mounted on loops, are flash frozen by dipping in liquid propane or freon at – 70°, or by instant exposure to N 2 gas at – 70°C. hexagonal ice

Centering the crystal in the beam whoops it’s off center. Fix it! s ray x “machine center” is the intersection of the beam and the two goniostat rotation axes. Must be set by manufacturer! To place crystal at machine center, rotate and watch the crystal. If it moves from side to side, it is off center. If it is off-center, we adjust the screws on the goniometer head.

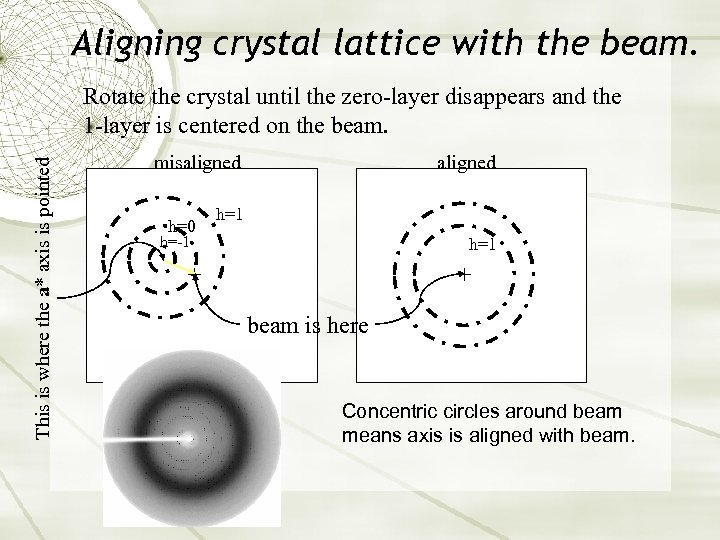Aligning crystal lattice with the beam. This is where the a* axis is pointed Rotate the crystal until the zero-layer disappears and the 1 -layer is centered on the beam. aligned misaligned h=0 h=1 h=-1 h=1 beam is here Concentric circles around beam means axis is aligned with beam.

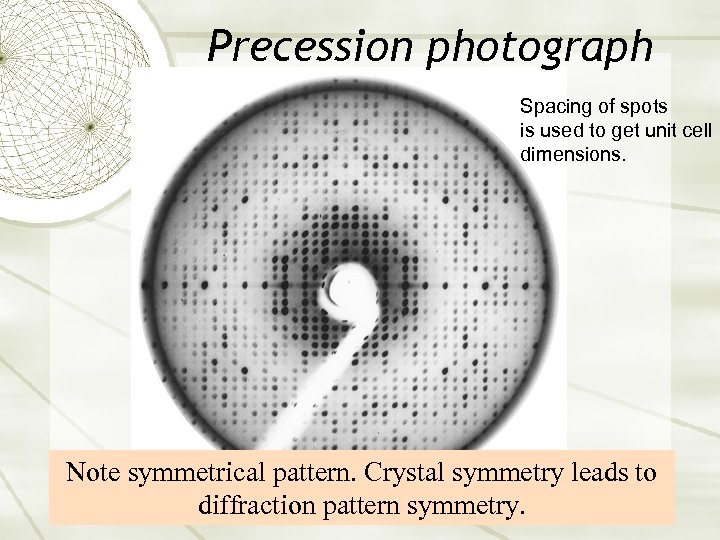Precession photograph Spacing of spots is used to get unit cell dimensions. Note symmetrical pattern. Crystal symmetry leads to diffraction pattern symmetry.

symmetry An object or function is symmetrical if a spatial transformation of it looks identical to the original. X This is rotated by 180° X This is the original

Symmetry operators A spatial transformation can be expressed as an operator that changes the coordinates of every point in the object the same way. Symmetry operators do not distort the object. In other words, the distance between any two points is the same before and after being moved by the symmetry operation. Here is the operator for a 180° rotation around Z. equivalent positions

REMINDER by the way 3 x 3 Matrix multiplication

Types of symmetry operations • Point of inversion • mirror plane • glide plane • rotation (2, 3, 4 or 6 -fold) • screw axis • lattice symmetry

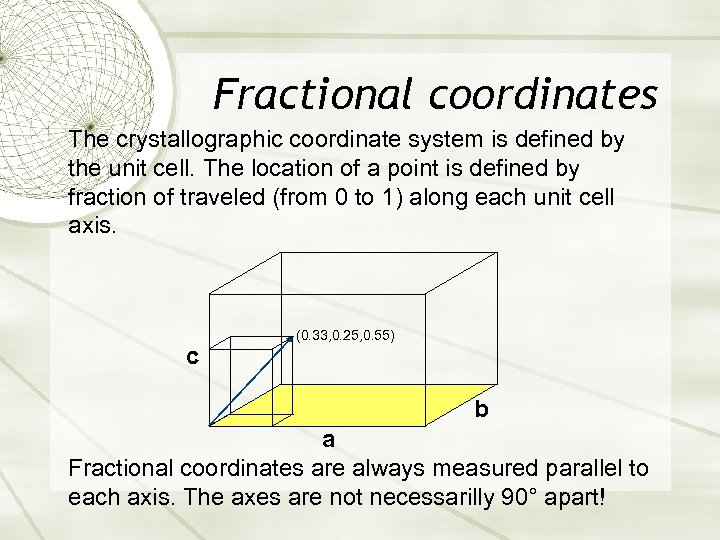Fractional coordinates The crystallographic coordinate system is defined by the unit cell. The location of a point is defined by fraction of traveled (from 0 to 1) along each unit cell axis. c (0. 33, 0. 25, 0. 55) b a Fractional coordinates are always measured parallel to each axis. The axes are not necessarilly 90° apart!

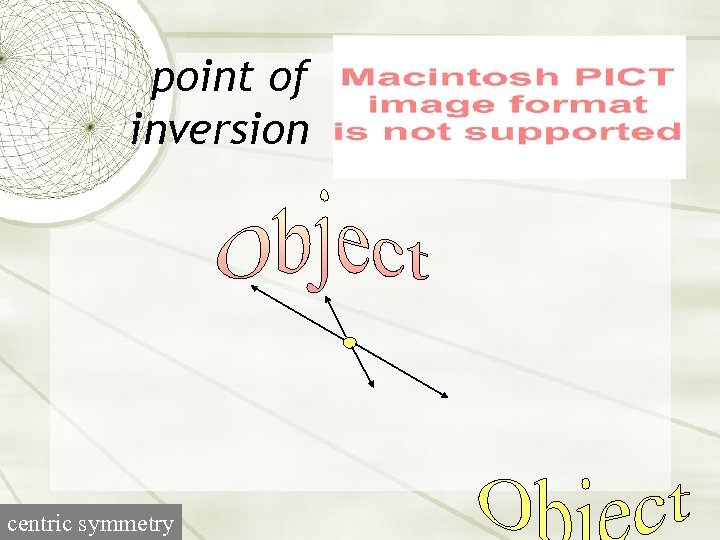point of inversion centric symmetry

mirror plane centric symmetry

glide plane x centric symmetry

rotation non-centric symmetry

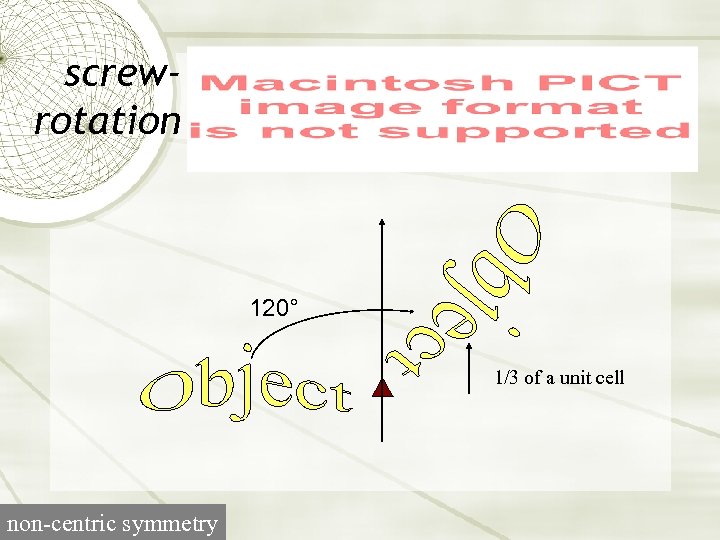screwrotation 120° 1/3 of a unit cell non-centric symmetry

Why proteins cannot have centric symmetry Mirror images and points of inversion cannot be re-created by pure rotations. Centric operations would change the chirality of chiral centers such as the alpha-carbon of amino acids or the ribosal carbons of RNA or DNA. R H C N C O

Rotational symmetry A 2 -fold (180°) rotation around the Z-axis

rotation

Rotation matrices. . . the mathematical description of a rotation. y axis of rotation (x’, y’) r atom starts here. . . rotates by b. . . goes here (x, y) x In polar coordinates, a rotation is the addition of angles.

REMINDER: sum of angles rules cos ( = cos sin ( = sin cos

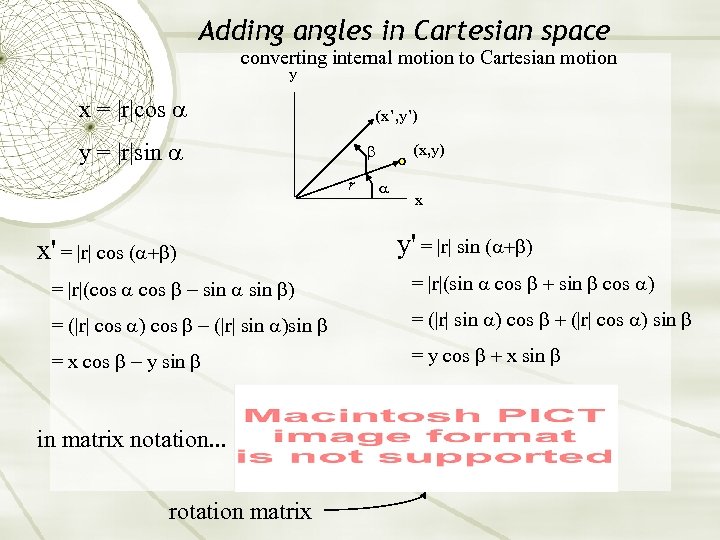Adding angles in Cartesian space converting internal motion to Cartesian motion y x = |r|cos (x’, y’) y = |r|sin r (x, y) x x' = |r| cos ( y' = |r| sin ( = |r|(cos sin = |r|(sin cos = (|r| cos |r| sin = (|r| sin cos |r| cos sin = x cos y sin = y cos x sin in matrix notation. . . rotation matrix

2 D rotation using matrix notation “row times column” x' = x cos y sin = = (|r| cos |r| sin = |r| cos ( y' = y cos x sin = (|r| sin cos |r| cos sin = |r| sin (

Transposing the matrix reverses the rotation To rotate the opposite direction, flip the matrix about the diagonal. the “transpose” inverse rotation matrix = transposed rotation matrix. . because cos + sin = 1

A 3 D rotation matrix Is the product of 2 D rotation matrices. Ro tat ion Ro tat aro un ion 3 D aro tat un dz -ax is ro dy -ax is ion

Example: Rotate v=(1. , 2. , 3. ) around Z by 60°, then rotate around Y by -60°

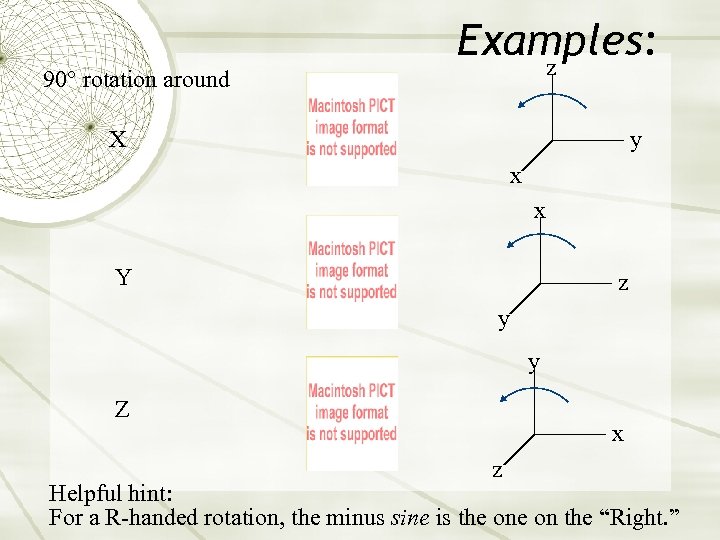90° rotation around Examples: z X y x x Y z y y Z x z Helpful hint: For a R-handed rotation, the minus sine is the on the “Right. ”

3 D angle conventions: axis of rotation: z’’ Order of rotations: Euler angles, a b g 3 x’ z 2 1 Polar angles, fyk z’’’’ 5 y’’’ 4 z’’ 3 Net rotation = -y’ -z 2 1

Properties of rotation matrices • Square, 2 x 2 or 3 x 3 • The product of any two rotation matrices is a rotation matrix • The inverse equals the transpose, R-1 = RT • orthogonality • The dot-product of any row or column with itself is one. • The dot-product of any row or column with a different row or column is zero. • |x| equals |Rx|, for any rotation R. More at http: //mathworld. wolfram. com/Rotation. Matrix. html

2 -fold rotation R 2 -fold symbol P 2 R 180° rotation. Called a 2 -fold because doing it twice brings you back to where you started. Equivalent positions in fractional coordinates: x, y, z -x, -y, z

3 -fold symbol R P 3 R R 3 -fold rotation In fractional coordinates: Equivalent positions : x, y, z -y, x-y, z -x+y, -x, z

4 -fold rotation R R P 4 R R 4 -fold symbol In fractional coordinates (same as orthogonal coords): Equivalent positions: x, y, z -y, x, z -x, -y, z y, -x, z

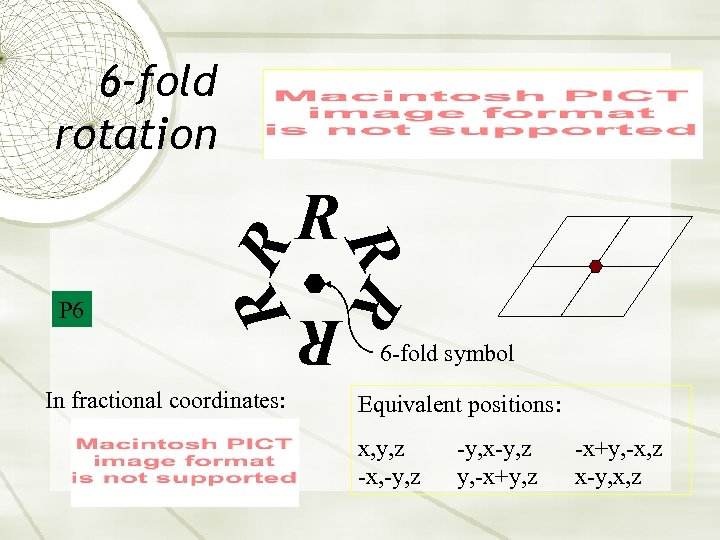6 -fold rotation R R In fractional coordinates: R P 6 RR R 6 -fold symbol Equivalent positions: x, y, z -x, -y, z -y, x-y, z y, -x+y, z -x+y, -x, z x-y, x, z

(a) In class exercise: rotating a point Choose a point r=(0. 1, 0. 2, 0. 3) [orthogonal coordinates] Rotate the point by 30° in x. Then rotate it by -90° in y. What are the new coordinates? (b) Choose a point r=(0. 1, 0. 2, 0. 3) [fractional coordinates] Multiply by the symmetry operator: What are the new fractional coordinates?

No 5 -fold symmetry in crystals? ? A crystal lattice must be space-filling and periodic.

Quasicrystals: 5 -fold point group symmetry, but no space group symmetry

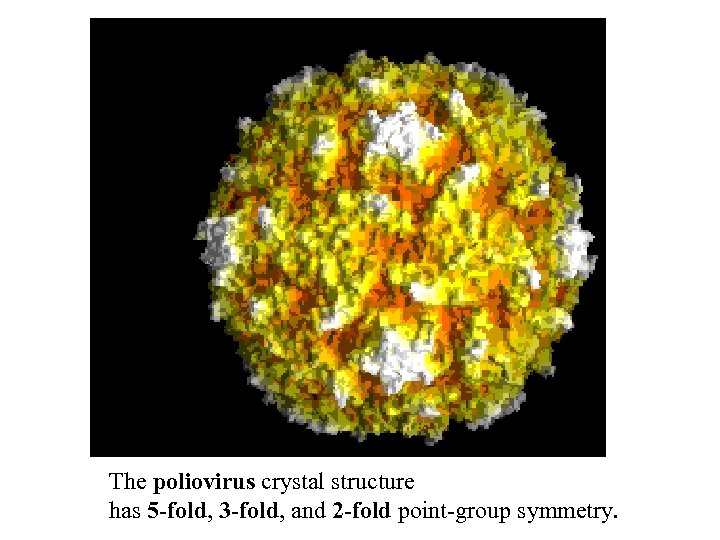The poliovirus crystal structure has 5 -fold, 3 -fold, and 2 -fold point-group symmetry.

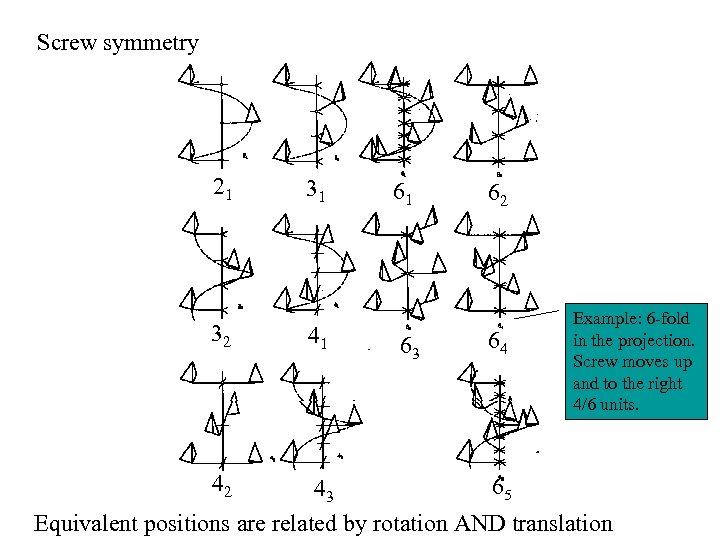Screw symmetry 21 32 42 31 41 61 63 62 64 Example: 6 -fold in the projection. Screw moves up and to the right 4/6 units. 65 43 Equivalent positions are related by rotation AND translation

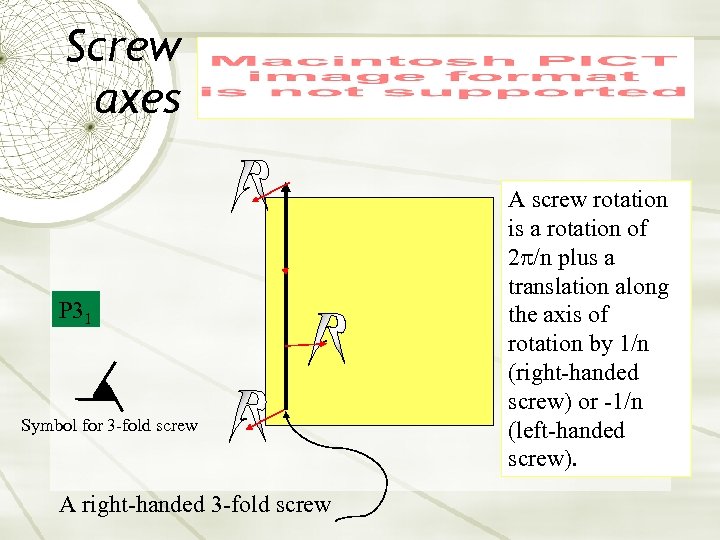Screw axes P 31 Symbol for 3 -fold screw A right-handed 3 -fold screw A screw rotation is a rotation of 2 p/n plus a translation along the axis of rotation by 1/n (right-handed screw) or -1/n (left-handed screw).

translational symmetry The crystal lattice is an example of translational symmetry. Equivalent positions are (x, y, z) and (x+1, y+1, z+1), in fractional coordinates. Space groups that have no other translational symmetry operations are called “primitive”. Space group letter “P” Space groups have letters indicating the type of translational symmetry: C (centered) F (face-centered) I (body-centered)

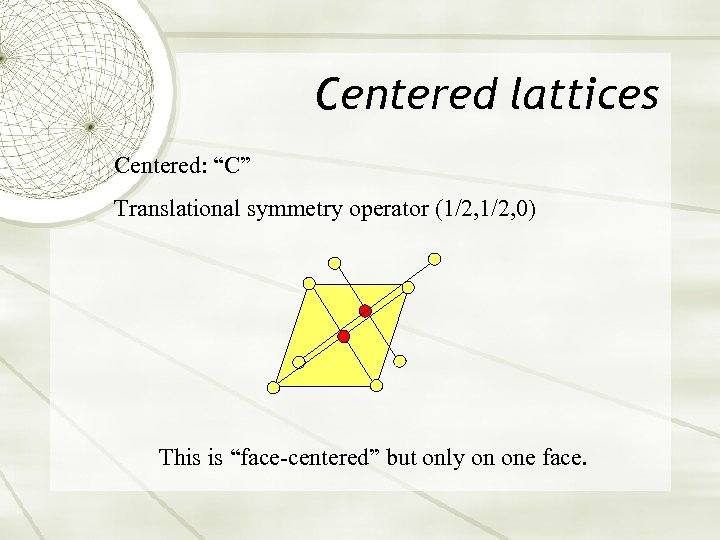Centered lattices Centered: “C” Translational symmetry operator (1/2, 0) This is “face-centered” but only on one face.

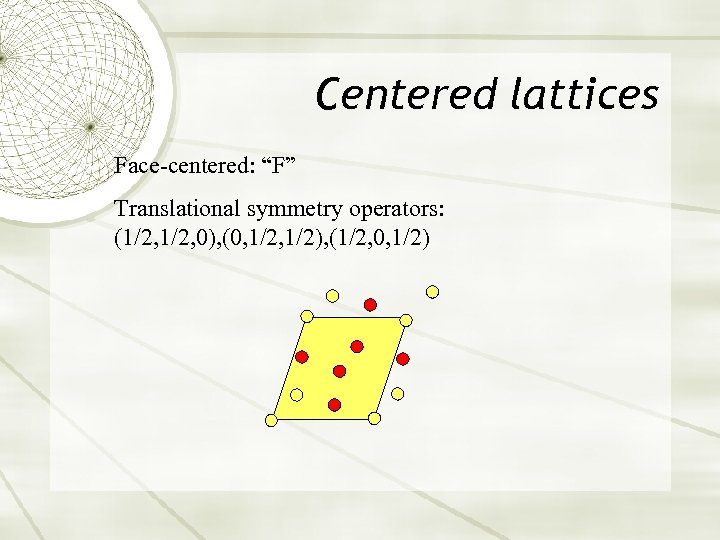Centered lattices Face-centered: “F” Translational symmetry operators: (1/2, 0), (0, 1/2), (1/2, 0, 1/2)

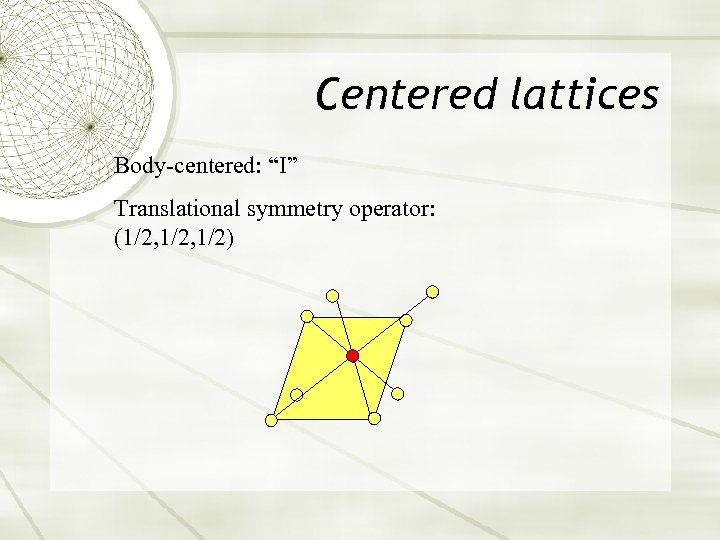Centered lattices Body-centered: “I” Translational symmetry operator: (1/2, 1/2)

Space groups A symmetry “group” is a set of symmetry operators that is closed, meaning any two operations, applied in succession, create a third operation that is part of the group. A “space group” is a symmetry group that includes lattice symmetry operators. All space groups implicitly include lattice operators: (± 1, ± 1)

The International Tables for Crystallography Equivalent positions: (x, y, z), (-x, -y, z+1/2)

Cell type P, C, I or F I=body centered Space groups I 4122 Principle axis of symmetry is 4 -fold screw Secondary axes of symmetry are proper 2 -folds

Group theory A space group is a closed set of operators. If you apply any two operators in succession. the result is another one of the operators in the group. Equivs for P 21: (x, y, z), (-x, -y, z+1/2)

Cubic space group P 213 x, y, z -x+1/2, -y, z+1/2 -x, y+1/2, z+1/2 x+1/2, -y+1/2, -z z, x, y z+1/2, -x+1/2, -y -z+1/2, -x, y+1/2 -z, x+1/2, -y+1/2 y, z, x -y, z+1/2, -x+1/2 y+1/2, -z+1/2, -x -y+1/2, -z, x+1/2

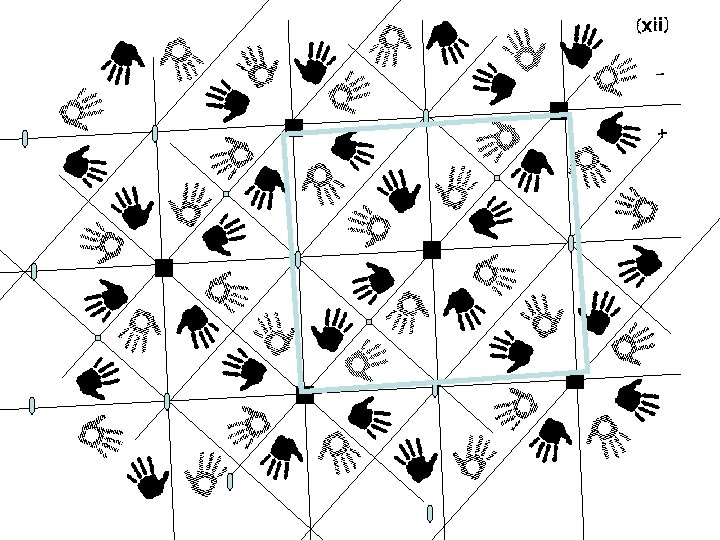
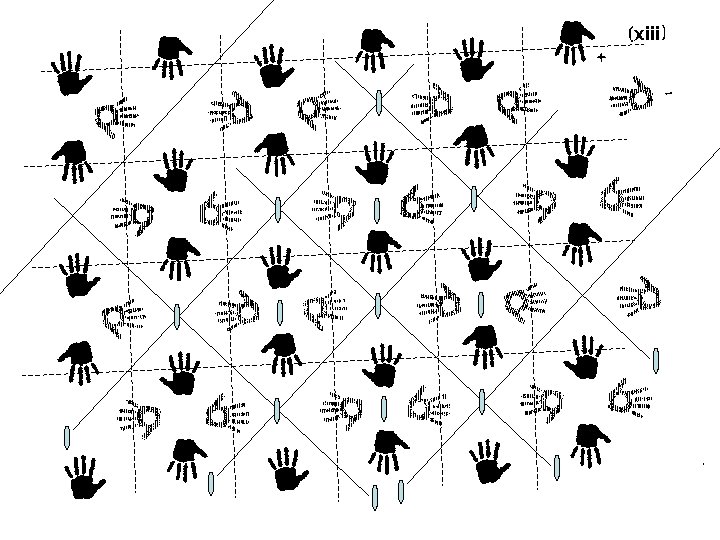
In class exercise: Find equivalent positions marie. epfl. ch/escher/ In class exercise: Use the Escher web sketch applet to find the equivalent positions for cm, p 4 mm, and p 6. Draw a dot at fractional coordinates (0. 1, 0. 2, 0. 3) What are the fractional coordinates of the equivalent positions? Write the 2 D symmetry operators (matrix and vector)

Point group symbols, etc.

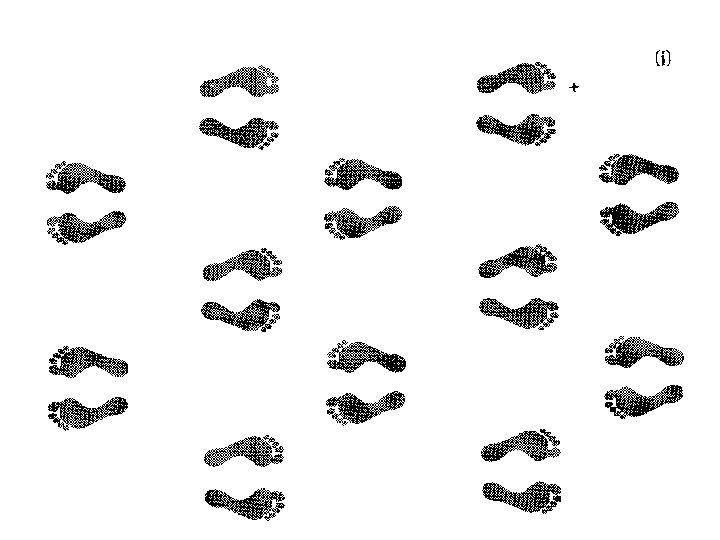
Finding symmetry in an image

Plane groups space group p 1