Lecture 18 -1 Eddy Current A current induced

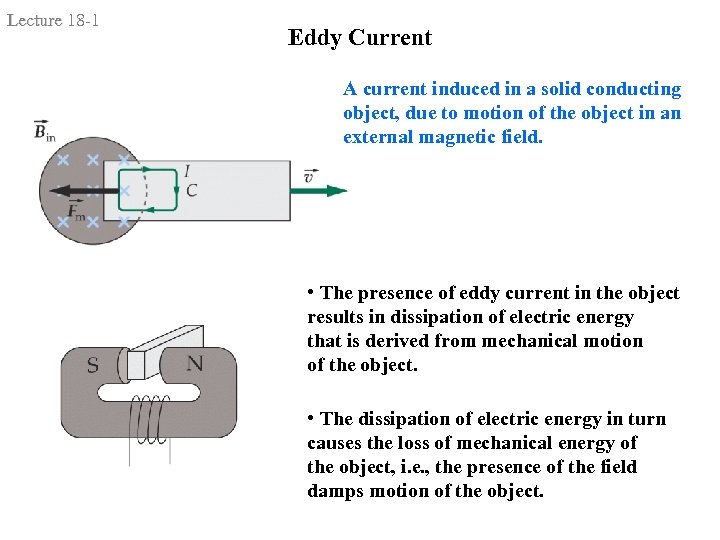Lecture 18 -1 Eddy Current A current induced in a solid conducting object, due to motion of the object in an external magnetic field. • The presence of eddy current in the object results in dissipation of electric energy that is derived from mechanical motion of the object. • The dissipation of electric energy in turn causes the loss of mechanical energy of the object, i. e. , the presence of the field damps motion of the object.

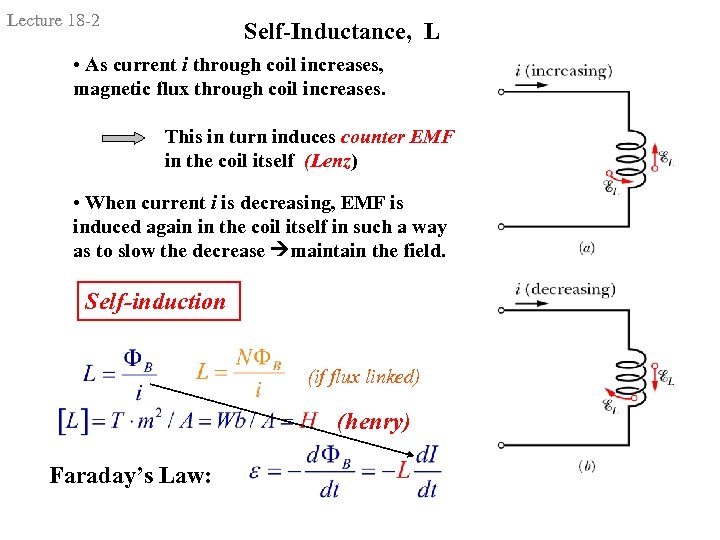Lecture 18 -2 Self-Inductance, L • As current i through coil increases, magnetic flux through coil increases. This in turn induces counter EMF in the coil itself (Lenz) • When current i is decreasing, EMF is induced again in the coil itself in such a way as to slow the decrease maintain the field. Self-induction (if flux linked) (henry) Faraday’s Law:

Lecture 18 -3 DEMO SELF INDUCTANCE 6 D-10

Lecture 18 -4 Inductance and Faraday’s Law (henry) + - INERTIA compare with This could have been a battery, instead. With the simplifying advantage that the applied ε is then ~constant.

Lecture 18 -5 Qualitative discussion of currents in L Note that if the initial current in an inductor, L, is ZERO, then it cannot instantly jump to a finite value when a potential difference is applied to it. Current I will “accelerate” from zero in a continuous way, just as the velocity of a mass at rest will accelerate in a continuous way under the influence of a force. At large times, the transients have died out, and since I is no longer changing, no voltage drop exists across the inductor L

Lecture 18 -6 Reading Quiz 1 Which of the following statements is incorrect? A| The inductance of a coil with N turns is proportional to N 2 turns. B| Like a capacitance (C) an inductor (L) depends on geometric factors and the nature of the material inside C and L. C| The potential across an inductor depends only on the magnitude of the current through the inductor. D| The magnetic energy stored in an inductor is proportional to the square of the current through the inductor.

Lecture 18 -7 Solenoid: Archetypical Inductor Current i flows through a long solenoid of radius r with N turns in length l For each turn For the solenoid or Al is the volume of the solenoid Inductance, like capacitance, only depends on geometry (if made of conductor and air). Add a magnetically polarizable material, increase L, just as adding an electrically polarizable material (dielectric) increases C.

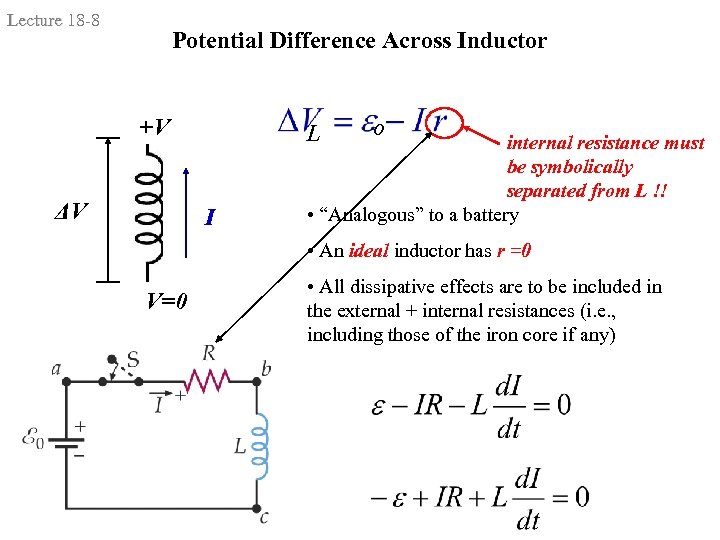Lecture 18 -8 Potential Difference Across Inductor +V ΔV L I o internal resistance must be symbolically separated from L !! • “Analogous” to a battery • An ideal inductor has r =0 V=0 • All dissipative effects are to be included in the external + internal resistances (i. e. , including those of the iron core if any)

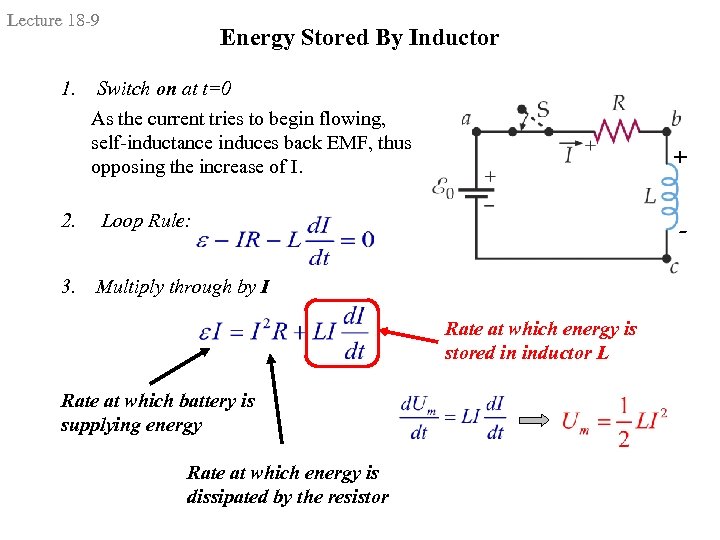Lecture 18 -9 1. 2. 3. Energy Stored By Inductor Switch on at t=0 As the current tries to begin flowing, self-inductance induces back EMF, thus opposing the increase of I. + Loop Rule: - Multiply through by I Rate at which energy is stored in inductor L Rate at which battery is supplying energy Rate at which energy is dissipated by the resistor

Lecture 18 -10 6 C 07 ENERGY STORED IN AN INDUCTOR

Lecture 18 -11 Where is the Energy Stored? • Energy must be stored in the magnetic field! Energy stored by a capacitor is stored in its electric field • Consider a long solenoid where area A • So energy density of the magnetic field is length l (Energy density of the electric field)

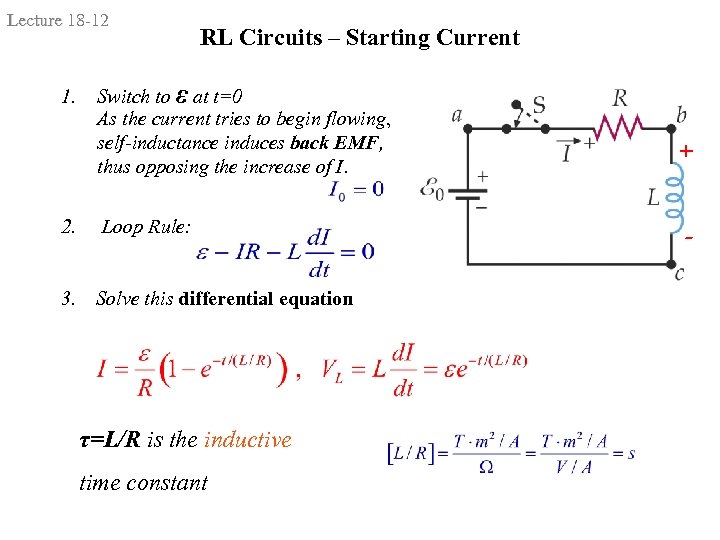Lecture 18 -12 1. 2. 3. RL Circuits – Starting Current Switch to ε at t=0 As the current tries to begin flowing, self-inductance induces back EMF, thus opposing the increase of I. Loop Rule: Solve this differential equation τ=L/R is the inductive time constant + -

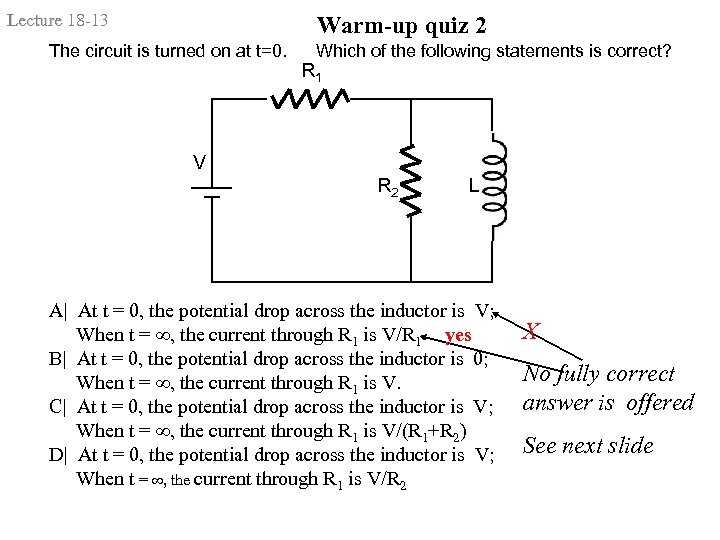Lecture 18 -13 Warm-up quiz 2 The circuit is turned on at t=0. Which of the following statements is correct? R 1 V R 2 L A| At t = 0, the potential drop across the inductor is V; When t = ∞, the current through R 1 is V/R 1 yes B| At t = 0, the potential drop across the inductor is 0; When t = ∞, the current through R 1 is V. C| At t = 0, the potential drop across the inductor is V; When t = ∞, the current through R 1 is V/(R 1+R 2) D| At t = 0, the potential drop across the inductor is V; When t = ∞, the current through R 1 is V/R 2 X No fully correct answer is offered See next slide

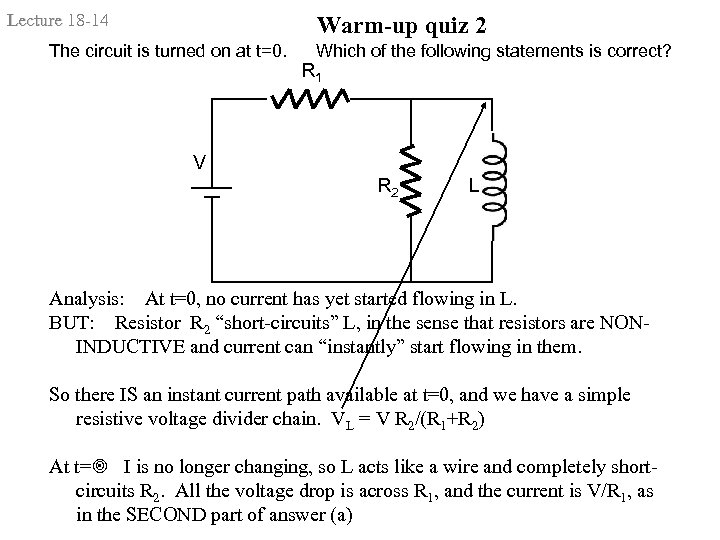Lecture 18 -14 Warm-up quiz 2 The circuit is turned on at t=0. Which of the following statements is correct? R 1 V R 2 L Analysis: At t=0, no current has yet started flowing in L. BUT: Resistor R 2 “short-circuits” L, in the sense that resistors are NONINDUCTIVE and current can “instantly” start flowing in them. So there IS an instant current path available at t=0, and we have a simple resistive voltage divider chain. VL = V R 2/(R 1+R 2) At t= I is no longer changing, so L acts like a wire and completely shortcircuits R 2. All the voltage drop is across R 1, and the current is V/R 1, as in the SECOND part of answer (a)

Lecture 18 -15 GROWTH AND DECAY OF CURRENT OF AN RL CIRCUIT 6 C-05

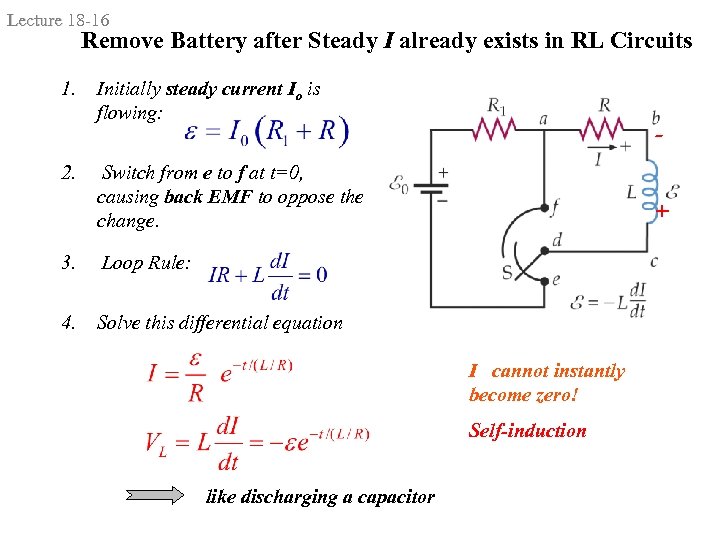Lecture 18 -16 Remove Battery after Steady I already exists in RL Circuits 1. 2. Initially steady current Io is flowing: - Switch from e to f at t=0, causing back EMF to oppose the change. 3. Loop Rule: 4. + Solve this differential equation I cannot instantly become zero! Self-induction like discharging a capacitor

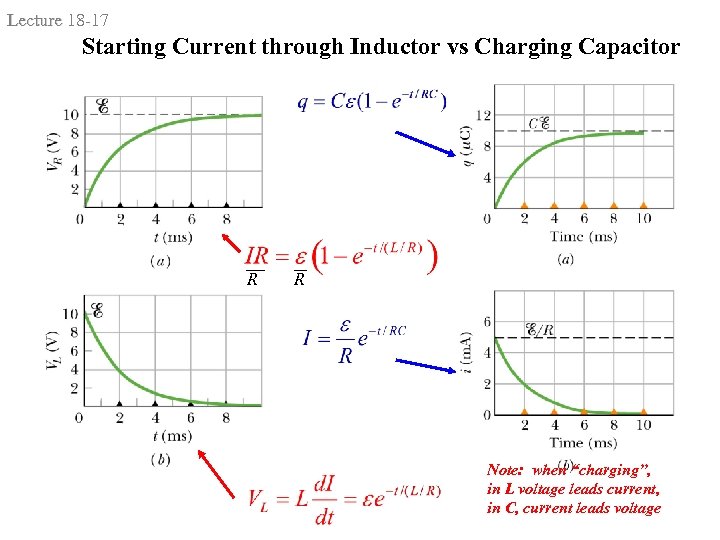Lecture 18 -17 Starting Current through Inductor vs Charging Capacitor R R Note: when “charging”, in L voltage leads current, in C, current leads voltage

Lecture 18 -18 Qualitative discussion of currents in L Note that if the initial current in an inductor, L, is ZERO, then it cannot instantly jump to a finite value when a potential difference is applied to it. Current I will “accelerate” from zero in a continuous way, just as the velocity of a mass at rest will accelerate in a continuous way under the influence of a force. At large times, the transients have died out, and since I is no longer changing, no voltage drop exists across the inductor L

Lecture 18 -19 Behavior of Inductors • Increasing Current – Initially, the inductor behaves like a battery connected in reverse. – After a long time, the inductor behaves like a conducting wire. • Decreasing Current – Initially, the inductor behaves like a “reinforcement” battery. – After a long time, the inductor behaves like a conducting wire.

Lecture 18 -20 Physics 241 March 22, 2011 9: 30 –Quiz 3 The switch in this circuit is initially open for a long time, and then closed at t = 0. What is the magnitude of the voltage across the inductor just after the switch is closed? a) zero b) V c) R / L d) V / R e) 2 V

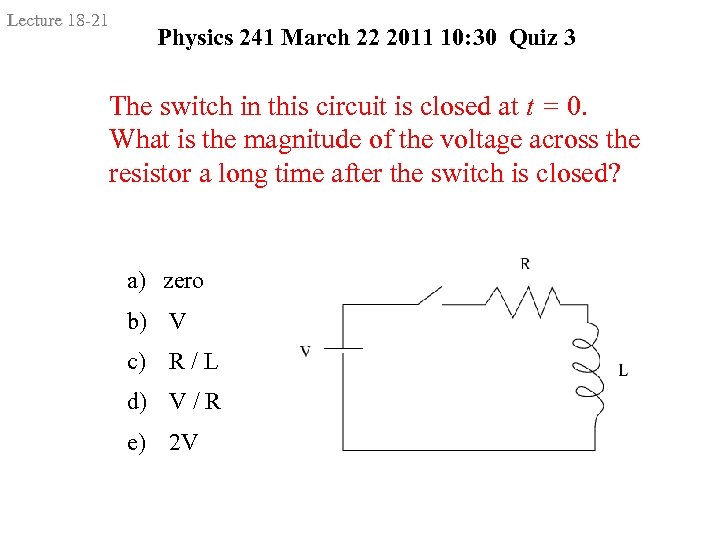Lecture 18 -21 Physics 241 March 22 2011 10: 30 Quiz 3 The switch in this circuit is closed at t = 0. What is the magnitude of the voltage across the resistor a long time after the switch is closed? a) zero b) V c) R / L d) V / R e) 2 V

Lecture 18 -22 Physics 241 March 22, 2011 11: 30–Quiz 3 The switch in this circuit has been open for a long time. Then the switch is closed at t = 0. What is the magnitude of the current through the resistor immediately after the switch is closed? a) zero b) V / L c) R / L d) V / R e) 2 V / R