Lecture 11 Stochastic Processes Topics Definitions

Lecture 11 – Stochastic Processes Topics • Definitions • Review of probability • Realization of a stochastic process • Continuous vs. discrete systems • Examples • Classification scheme 8/14/04

Basic Definitions Stochastic process: System that changes over time in an uncertain manner State: Snapshot of the system at some fixed point in time Transition: Movement from one state to another Examples • Automated teller machine (ATM) • Printed circuit board assembly operation • Runway activity at airport 2

Elements of Probability Theory Experiment: Any situation where the outcome is uncertain. Sample Space, S: All possible outcomes of an experiment (we will call it “state space”). Event: Any collection of outcomes (points) in the sample space. A collection of events E 1, E 2, …, En is said to be mutually exclusive if Ei Ej = for all i ≠ j = 1, …, n. Random Variable: Function or procedure that assigns a real number to each outcome in the sample space. Cumulative Distribution Function (CDF), F(·): Probability distribution function for the random variable X such that F(a) = Pr{X ≤ a}. 3

Model Components (continued) Time: Either continuous or discrete parameter. State: Describes the attributes of a system at some point in time. s = (s 1, s 2, . . . , sv); for ATM example s = (n) Convenient to assign a unique nonnegative integer index to each possible value of the state vector. We call this X and require that for each s X. For ATM example, X = n. In general, Xt is a random variable. 4

Activity: Takes some amount of time – duration. Culminates in an event. For ATM example service completion. Transition: Caused by an event and results in movement from one state to another. For ATM example, Stochastic Process: A collection of random variables {Xt}, where t T = {0, 1, 2, . . . }. 5

Markovian Property Given that the present state is known, the conditional probability of the next state is independent of the states prior to the present state. Present state at time t is i: Xt = i Next state at time t + 1 is j: Xt+1 = j Conditional Probability Statement of Markovian Property: Pr{Xt+1 = j | X 0 = k 0, X 1 = k 1, …, Xt = i} = Pr{Xt+1 = j | Xt = i} for t = 0, 1, …, and all possible sequences i, j, k 0, k 1, . . . , kt– 1. 6

Realization of the Process Deterministic Process Time between arrivals Pr{ta } = 0, < 1 min Time for servicing customer Pr{ts } = 0, < 0. 75 min = 1, 1 min = 1, 0. 75 min Arrivals occur every minute. Processing takes exactly 0. 75 minutes. Number in system, n (no transient response) 7

Realization of the Process (continued) Stochastic Process Time for servicing customer Pr{ts } = 0, < 0. 75 min = 0. 6, 0. 75 1. 5 min = 1, 1. 5 min Number in system, n 8

Birth and Death Processes Pure Birth Process; e. g. , Hurricanes Pure Death Process; e. g. , Delivery of a truckload of parcels Birth-Death Process; e. g. , Repair shop for taxi company 9

Queueing Systems Queue Discipline: Order in which customers are served; FIFO, LIFO, Random, Priority Five Field Notation: Arrival distribution / Service distribution / Number of servers / Maximum number in the system / Number in the calling population 10

Queueing Notation Distributions (interarrival and service times) M = Exponential D = Constant time Ek = Erlang GI = General independent (arrivals only) G = General Parameters s = number of servers K = Maximum number in system N = Size of calling population 11

Characteristics of Queues Infinite queue: e. g. , Mail order company (GI/G/s) Finite queue: e. g. , Airline reservation system (M/M/s/K) a. Customer arrives but then leaves b. No more arrivals after K 12

Characteristics of Queues (continued) Finite input source: e. g. , Repair shop for trucking firm (N vehicles) with s service bays and limited capacity parking lot (K – s spaces). Each repair takes 1 day (GI/D/s/K/N). In this diagram N = K so we have GI/D/s/K/K system. 13

Examples of Stochastic Processes Service Completion Triggers an Arrival: e. g. , multistage assembly process with single worker, no queue. state = 0, worker is idle state = k, worker is performing operation k = 1, . . . , 5 14

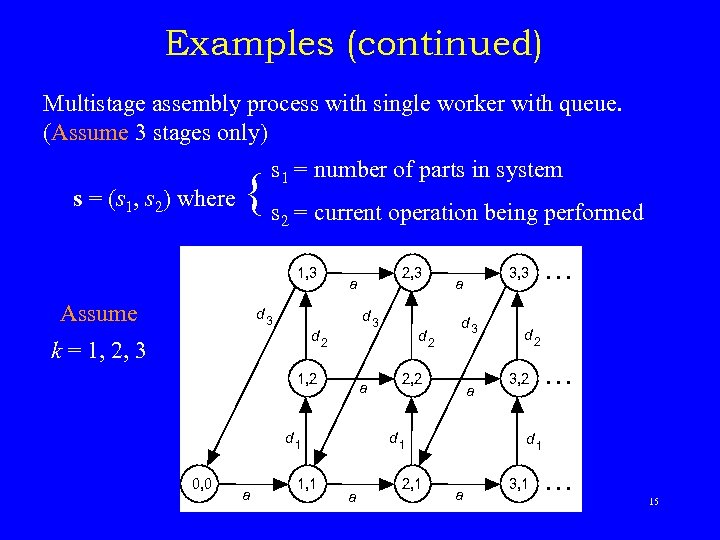Examples (continued) Multistage assembly process with single worker with queue. (Assume 3 stages only) s = (s 1, s 2) where s 1 = number of parts in system { s = current operation being performed 2 1, 3 Assume d 3 d 2 k = 1, 2, 3 1, 2 a d 1 0, 0 a 1, 1 2, 3 a d 2 d 3 2, 2 a d 1 a 2, 1 3, 3 a … d 2 3, 2 … d 1 a 3, 1 … 15

Queueing Model with Two Servers, One Operation 0 if server i is idle { 1 if server i is busy s = number in queue s = (s 1, s 2 , s 3) where si = 1, 2 3 Statetransition network 16

Series System with No Queues Component Notation State Definition s = (s 1, s 2 , s 3) 0 if server i is idle i = s { 1 if server i is busy for i = 1, 2, 3 State space S = { (0, 0, 0), (1, 0, 0), . . . , (0, 1, 1), (1, 1, 1) } The state space consists of all possible binary vectors of 3 components. Activities Y = {a, d 1, d 2 , d 3} a = arrival at operation 1 dj = completion of operation j for j = 1, 2, 3 17

Transitions for Markov Processes Exponential interarrival and service times (M/M/s) State space: S = {1, 2, . . . } Probability of going from state i to state j in one move: pij State-transition matrix P = Theoretical requirements: 0 pij 1, j pij = 1, i = 1, …, m 18

Single Channel Queue – Two Kinds of Service Bank teller: normal service (d), travelers checks (c), idle (i) Let p = portion of customers who buy checks after normal service s 1 = number in system s 2 = status of teller, where s 2 {i, d, c} Statetransition network 19

Part Processing with Rework Consider a machining operation in which there is a 0. 4 probability that upon completion, a processed part will not be within tolerance. Machine is in one of three states: 0 = idle, 1 = working on part for first time, 2 = reworking part. State-transition network a = arrival s 1 = service completion from state 1 s 2 = service completion from state 2 20

Markov Chains • A discrete state space • Markovian property for transitions • One-step transition probabilities, pij, remain constant over time (stationary) Example: Game of Craps Roll 2 dice: Win = 7 or 11; Loose = 2, 3, 12; otherwise 4, 5, 6, 8, 9, 10 (called point) and roll again win if point loose if 7 otherwise roll again, and so on. (There are other possible bets not include here. ) 21

State-Transition Network for Craps 22

Transition Matrix for Game of Craps 23

State-Transition Network for Simple Markov Chain 24

Classification of States Accessible: Possible to go from state i to state j (path exists in the network from i to j). Two states communicate if both are accessible from each other. A system is irreducible if all states communicate. State i is recurrent if the system will return to it after leaving some time in the future. If a state is not recurrent, it is transient. 25

Classification of States (continued) A state is periodic if it can only return to itself after a fixed number of transitions greater than 1 (or multiple of a fixed number). A state that is not periodic is aperiodic. a. Each state visited every 3 iterations b. Each state visited in multiples of 3 iterations 26

Classification of States (continued) An absorbing state is one that locks in the system once it enters. This diagram might represent the wealth of a gambler who begins with $2 and makes a series of wagers for $1 each. Let ai be the event of winning in state i and di the event of losing in state i. There are two absorbing states: 0 and 4. 27

Classification of States (continued) Class: set of states that communicate with each other. A class is either all recurrent or all transient and may be either all periodic or aperiodic. States in a transient class communicate only with each other so no arcs enter any of the corresponding nodes in the network diagram from outside the class. Arcs may leave, though, passing from a node in the class to one outside. 28

Illustration of Concepts Example 1 Every pair of states communicates, forming a single recurrent class; however, the states are not periodic. Thus the stochastic process is aperiodic and irreducible. 29

Illustration of Concepts Example 2 States 0 and 1 communicate and for a recurrent class. States 3 and 4 form separate transient classes. State 2 is an absorbing state and forms a recurrent class. 30

Illustration of Concepts Example 3 Every state communicates with every other state, so we have irreducible stochastic process. Periodic? Yes, so Markov chain is irreducible and periodic. 31

What you Should know about Stochastic Processes • What a state is • What a realization is (stationary vs. transient) • What the difference is between a continuous and discrete-time system • What the common applications are • What a state-transition matrix is • How systems are classified 32