Lecture 10 Inputs and Production Functions cont

Lecture # 10 Inputs and Production Functions (cont. ) Lecturer: Martin Paredes

The Production Function (conclusion) l Elasticity of Substitution 2. Some Special Functional Forms 3. Returns to Scale 4. Technological Progress 1. 2

Definition: The elasticity of substitution measures how the capital-labor ratio, K/L, changes relative to the change in the MRTSL, K. = % (K/L) = d (K/L). MRTSL, K % MRTSL, K d MRTSL, K (K/L) l In other words, it measures how quickly the MRTSL, K changes as we move along an isoquant. 3

Notes: l In other words, the elasticity of substitution measures how quickly the MRTSL, K changes as we move along an isoquant. l The capital-labor ratio (K/L) is the slope of any ray from the origin to the isoquant. 4

Example: Elasticity of Substitution • Suppose that… At point A: At point B: MRTSAL, K = 4 MRTSBL, K = 1 KA/LA = 4 KB/LB = 1 • What is the elasticity of substitution? 5

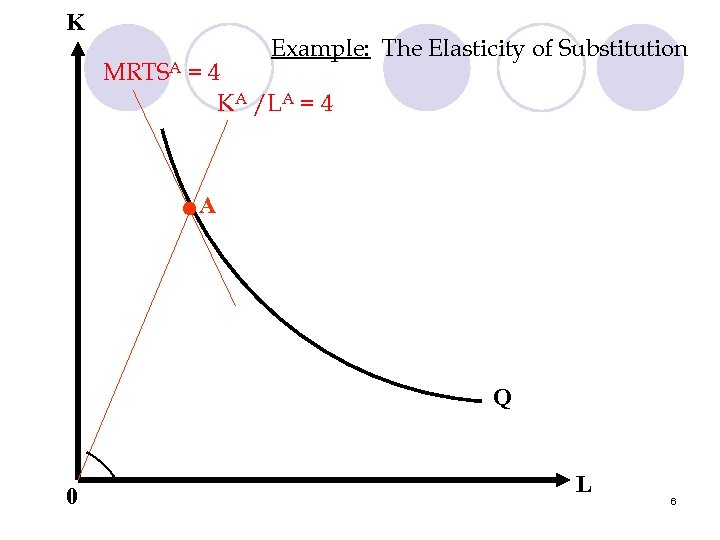K Example: The Elasticity of Substitution MRTSA = 4 KA /LA = 4 • A Q 0 L 6

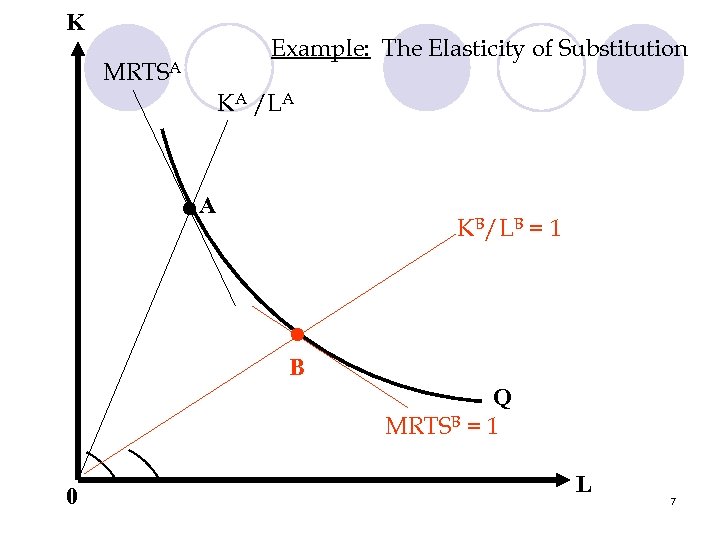K MRTSA Example: The Elasticity of Substitution KA /LA • A KB/LB = 1 • B Q MRTSB = 1 0 L 7

Example: Elasticity of Substitution % (K/L) = -3 / 4 = - 75% % MRTSL, K = -3 / 4 = - 75% = % (K/L) = % MRTSL, K - 75% = 1 - 75% 8

Linear Production Function 2. Q = a. L + b. K 3. where a, b are positive constants 1. l Properties: l MRTSL, K = MPL = a (constant) MPK b l Constant returns to scale l = 9

K Example: Linear Production Function Q 0 0 L 10

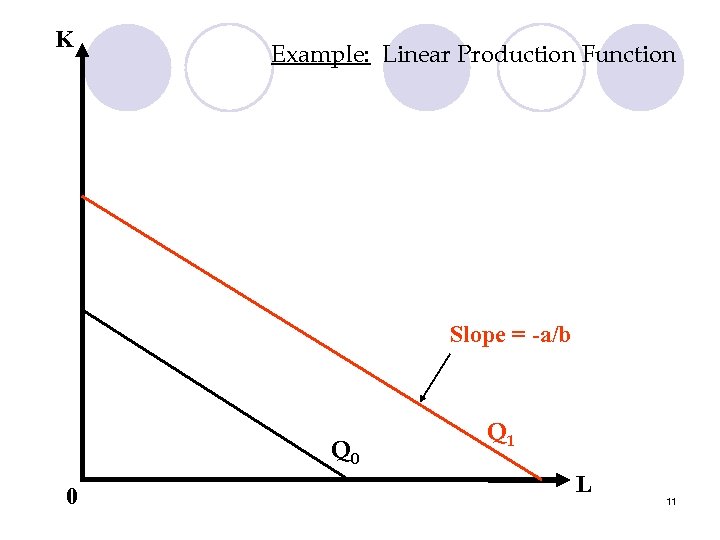K Example: Linear Production Function Slope = -a/b Q 0 0 Q 1 L 11

2. Fixed Proportions Production Function Q = min(a. L, b. K) where a, b are positive constants Also called the Leontief Production Function l L-shaped isoquants l Properties: l MRTSL, K = 0 or undefined l =0 l 12

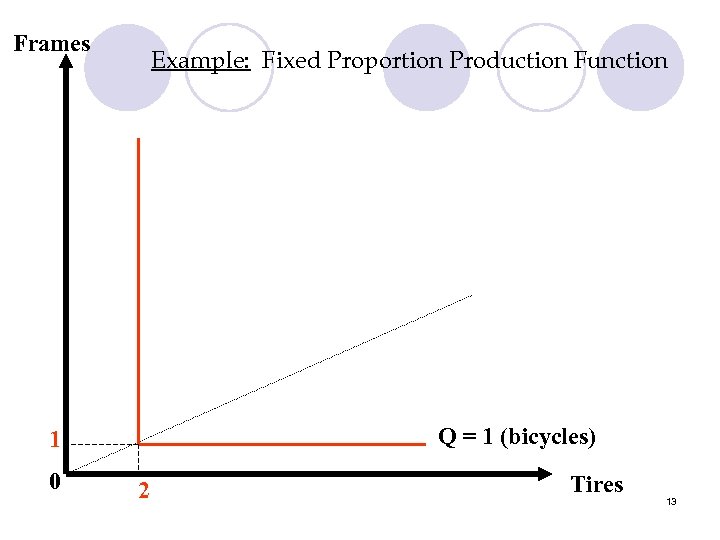Frames Example: Fixed Proportion Production Function Q = 1 (bicycles) 1 0 2 Tires 13

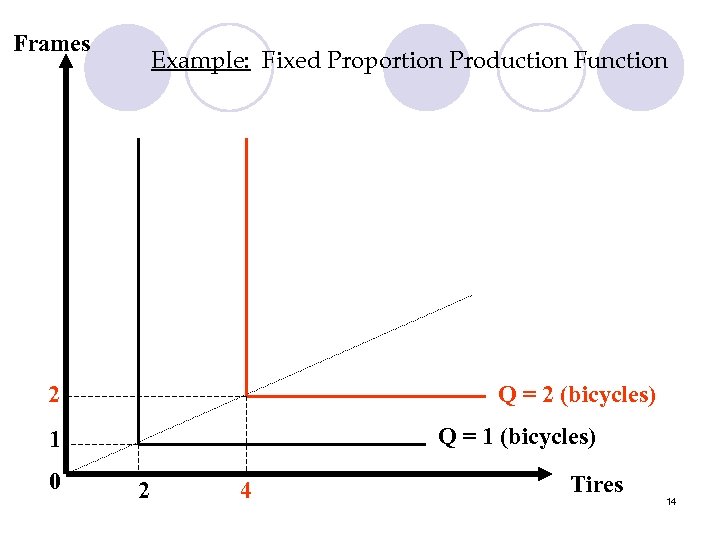Frames Example: Fixed Proportion Production Function 2 Q = 2 (bicycles) Q = 1 (bicycles) 1 0 2 4 Tires 14

3. Cobb-Douglas Production Function Q = AL K where A, , are all positive constants l Properties: l MRTSL, K = MPL = AL -1 K = K MPK AL K -1 L l =1 15

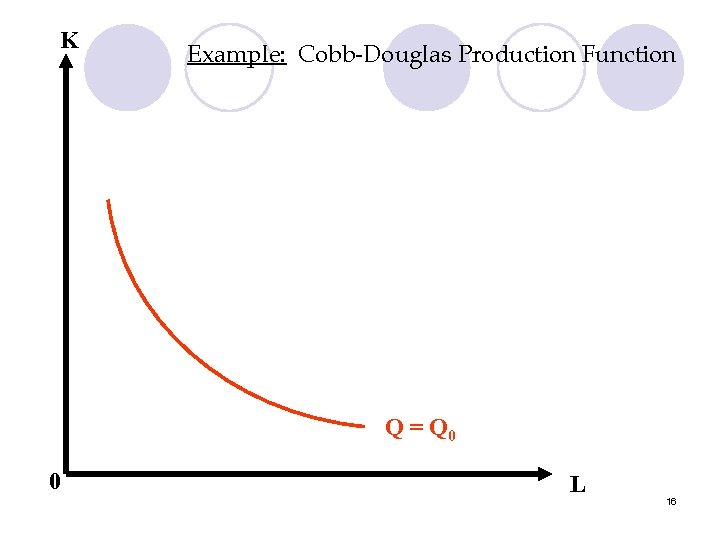K Example: Cobb-Douglas Production Function Q = Q 0 0 L 16

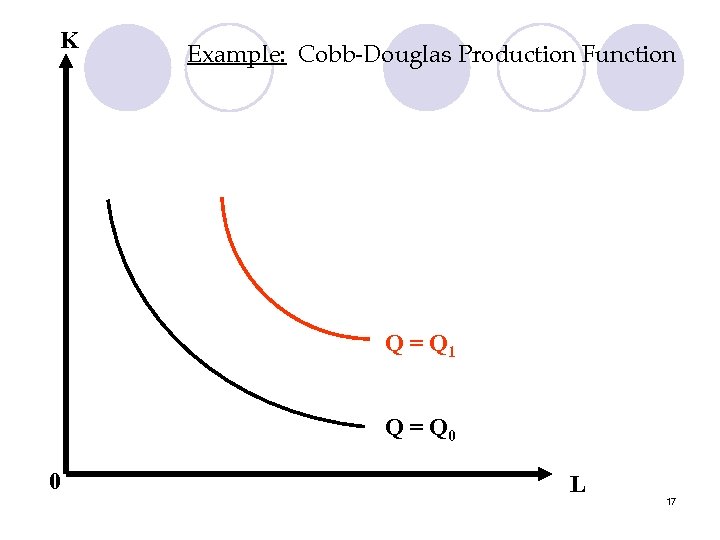K Example: Cobb-Douglas Production Function Q = Q 1 Q = Q 0 0 L 17

Constant Elasticity of Substitution Production Function 5. Q = (a. L + b. K )1/ where , , are all positive constants 4. In particular, = ( -1)/ l Properties: l If = 0 => Leontieff case l If = 1 => Cobb-Douglas case l If = => Linear case l 18

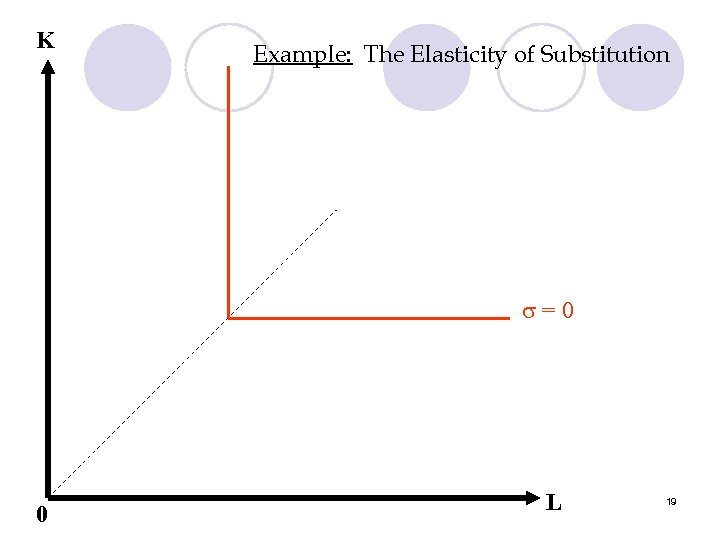K Example: The Elasticity of Substitution =0 0 L 19

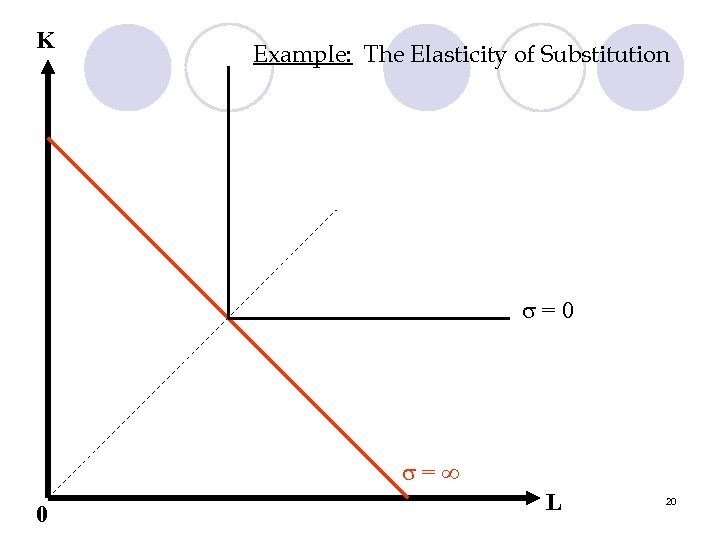K Example: The Elasticity of Substitution =0 = 0 L 20

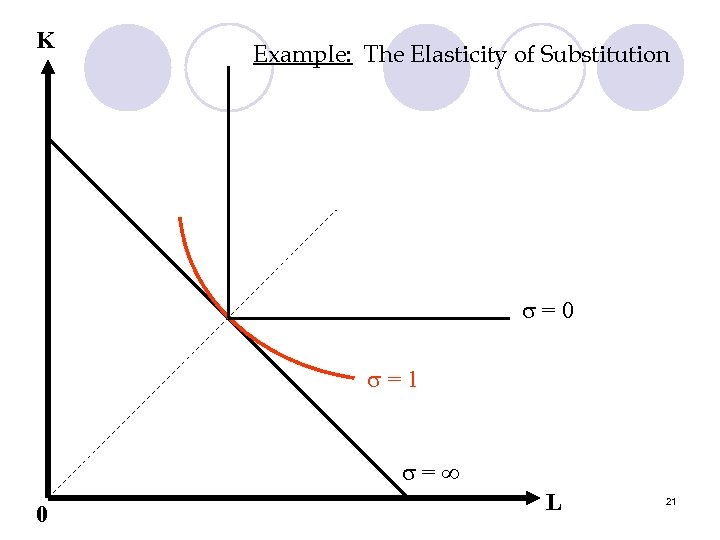K Example: The Elasticity of Substitution =0 =1 = 0 L 21

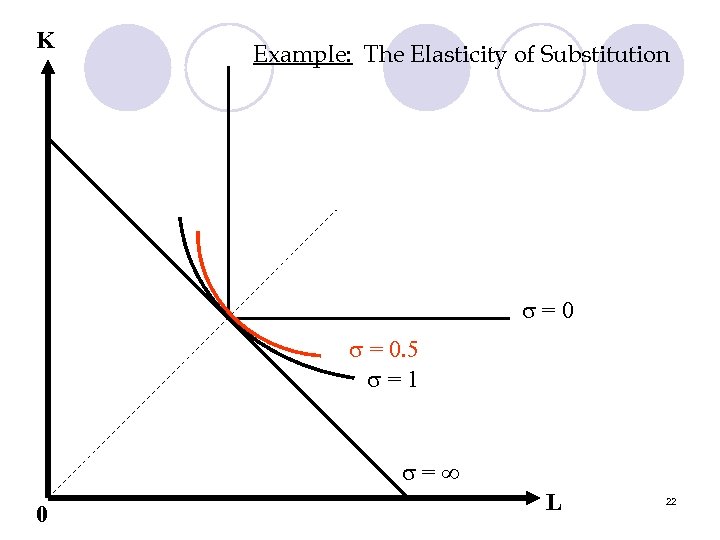K Example: The Elasticity of Substitution =0 = 0. 5 =1 = 0 L 22

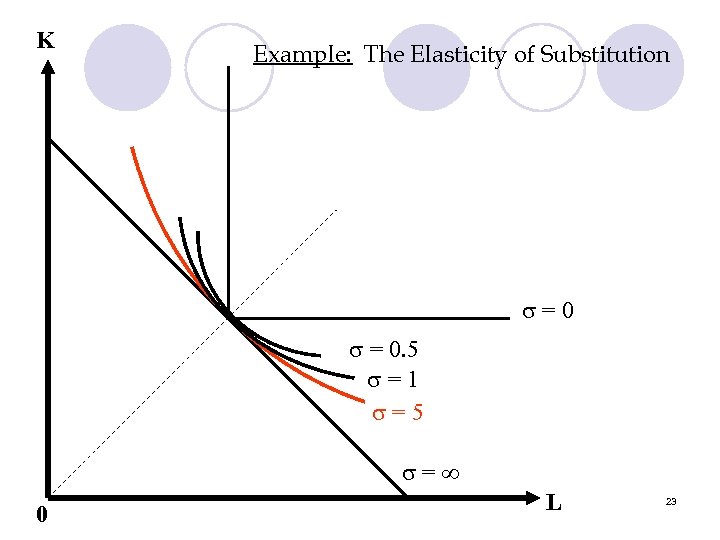K Example: The Elasticity of Substitution =0 = 0. 5 =1 = 5 = 0 L 23

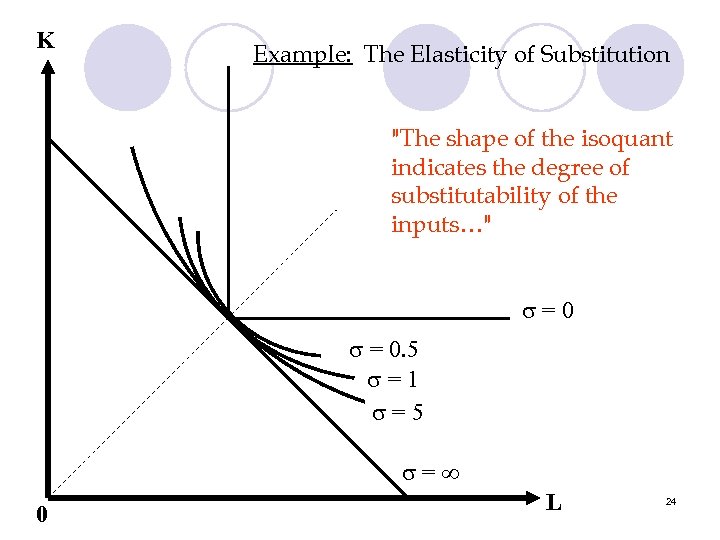K Example: The Elasticity of Substitution "The shape of the isoquant indicates the degree of substitutability of the inputs…" =0 = 0. 5 =1 = 5 = 0 L 24

Definition: Returns to scale is the concept that tells us the percentage increase in output when all inputs are increased by a given percentage. Returns to scale = % Output. % ALL Inputs 25

Suppose we increase ALL inputs by a factor l Suppose that, as a result, output increases by a factor . l Then: 1. If > ==> Increasing returns to scale 2. If = ==> Constant returns to scale 3. If < ==> Decreasing returns to scale. l 26