3c3b7f936fb5066a13e66f6964bb5742.ppt
- Количество слайдов: 49

Lecture 1 Distributed Algorithms Gadi Taubenfeld INTRODUCTION Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 1

This lecture is based on Chapter 1 from the textbook A note on the use of these ppt slides: I am making these slides freely available to all (faculty, students, readers). They are in Power. Point form so you can add, modify, and delete slides and slide content to suit your needs. They obviously represent a lot of work on my part. In return for use, I only ask the following: q That you mention their source, after all, I would like people to use my book! q That you note that they are adapted from (or perhaps identical to) my slides, and note my copyright of this material. Thanks and enjoy! Gadi Taubenfeld All material copyright 2011 Gadi Taubenfeld, All Rights Reserved To get the most updated version of these slides go to: http: //www. faculty. idc. ac. il/gadi/book. htm Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 2

Synchronization q Type of synchronization Contention m Coordination q Why synchronization is difficult? m Easy between humans m Communication between computers is restricted m • reading and writing of notes • sending and receiving messages Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 3

The Too-Much-Milk Problem Time Alice Bob 5: 00 Arrive Home 5: 05 Look in fridge; no milk 5: 10 Leave for grocery 5: 15 Arrive home 5: 20 Arrive at grocery Look in fridge; no milk 5: 25 Buy milk Leave for grocery 5: 30 Arrive home; put milk in fridge 3: 40 3: 45 Lecture 1 Buy milk Arrive home; too much milk! Distributed Algorithms Gadi Taubenfeld © 2011 4

Solving the Too-Much-Milk Problem Correctness properties q Mutual Exclusion: Only one person buys milk at a time q Progress: Someone always buys milk if it is needed Lecture 1 Communication primitives q Leave a note (set a flag) q Remove a note (reset a flag) q Read a note (test the flag) Distributed Algorithms Gadi Taubenfeld © 2011 5

Important Distinction q Safety Property Nothing bad happens ever m Example: mutual exclusion q Liveness Property m Something good happens eventually m Example: progress m Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 6
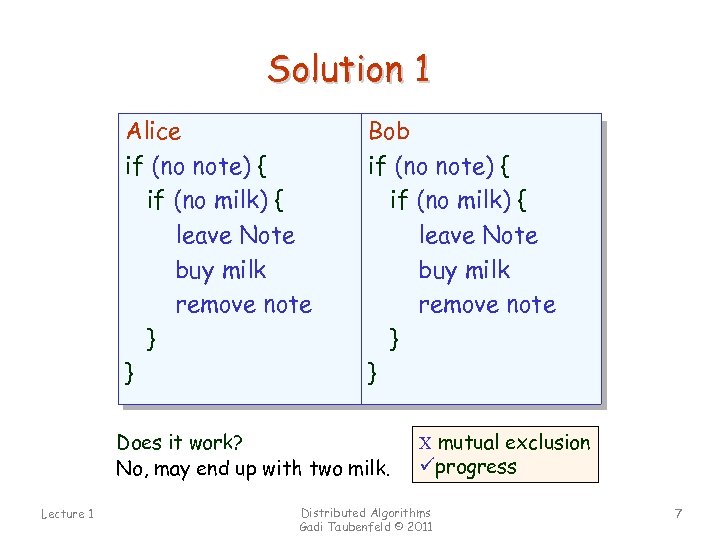
Solution 1 Alice if (no note) { if (no milk) { leave Note buy milk remove note } } Bob if (no note) { if (no milk) { leave Note buy milk remove note } } Does it work? No, may end up with two milk. Lecture 1 C mutual exclusion üprogress Distributed Algorithms Gadi Taubenfeld © 2011 7

Solution 2 Using labeled notes Alice leave note A if (no note B) { if (no milk) {buy milk} } remove note A Does it work? No, may end up with no milk. Lecture 1 Bob leave note B if (no note A) { if (no milk) {buy milk} } remove note B ümutual exclusion C progress Distributed Algorithms Gadi Taubenfeld © 2011 8
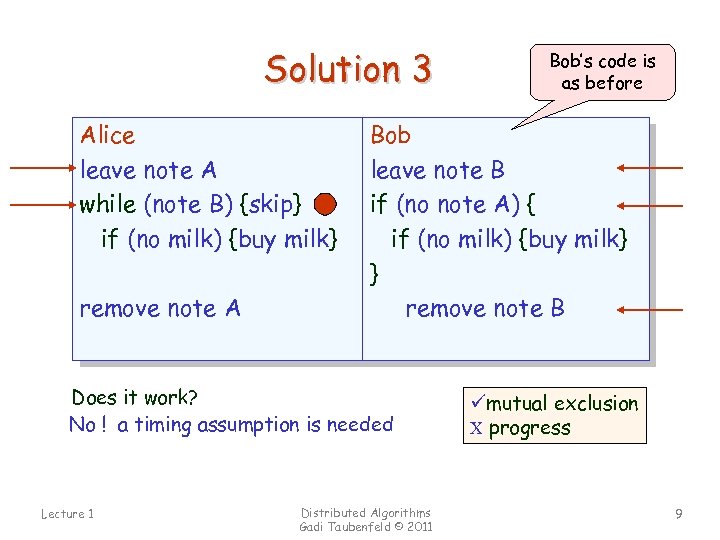
Solution 3 Alice leave note A while (note B) {skip} if (no milk) {buy milk} remove note A Bob leave note B if (no note A) { if (no milk) {buy milk} } remove note B Does it work? No ! a timing assumption is needed Lecture 1 Bob’s code is as before Distributed Algorithms Gadi Taubenfeld © 2011 ümutual exclusion C progress 9

Is solution #3 a good solution? No q A timing assumption is needed! q Unfair to one of the processes q It is asymmetrical and complicated q Alice is busy waiting – consuming CPU cycles without accomplishing useful work Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 10
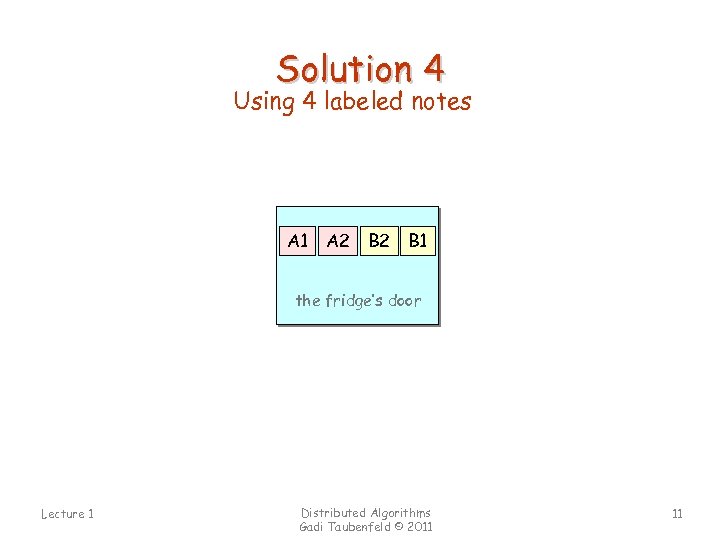
Solution 4 Using 4 labeled notes A 1 A 2 B 1 the fridge’s door Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 11
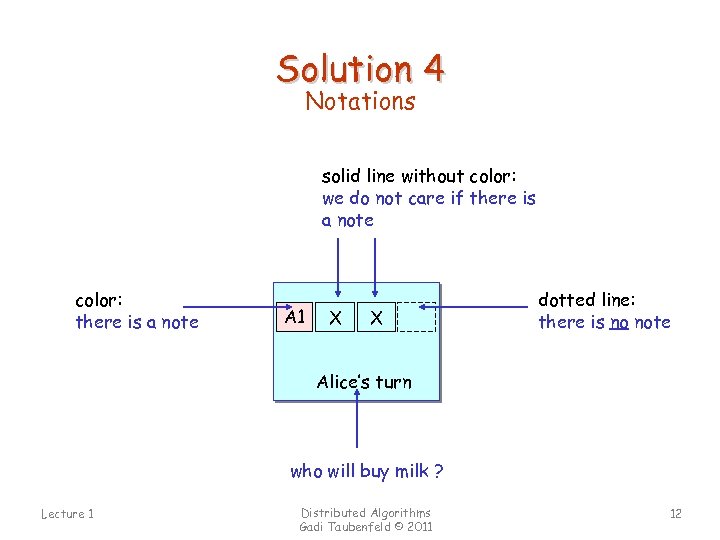
Solution 4 Notations solid line without color: we do not care if there is a note color: there is a note A 1 A 2 B 2 X X dotted line: there is no note Alice’s turn who will buy milk ? Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 12
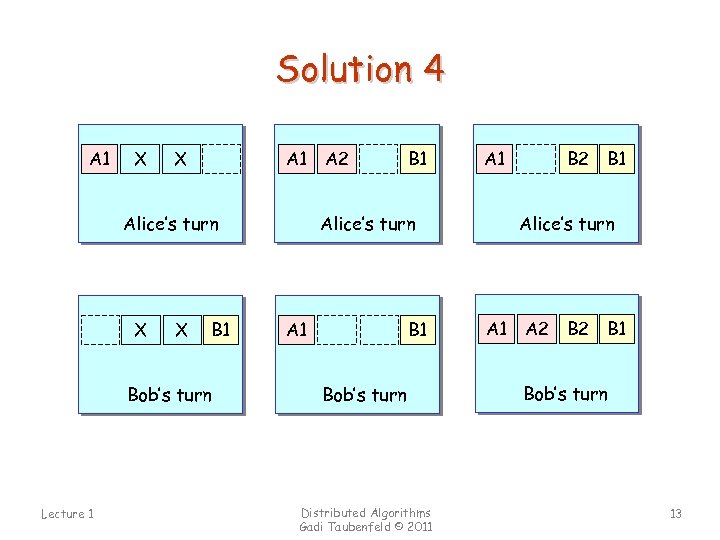
Solution 4 A 1 A 2 B 2 X X Alice’s turn B 2 A 2 B 1 X X Bob’s turn Lecture 1 A 2 B 1 Alice’s turn A 1 A 2 B 1 Bob’s turn Distributed Algorithms Gadi Taubenfeld © 2011 A 2 B 1 Alice’s turn A 1 A 2 B 1 Bob’s turn 13

Solution 4 Alice leave A 1 if B 2 {leave A 2} else {remove A 2} while B 1 and ((A 2 and B 2) or (no A 2 and no B 2)) {skip} if (no milk) {buy milk} remove A 1 Bob leave B 1 if (no A 2) {leave B 2} else {remove B 2} while A 1 and ((A 2 and no B 2) or (no A 2 and B 2)) {skip} if (no milk) {buy milk} remove note B 1 A correct, fair, symmetric algorithm! Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 14
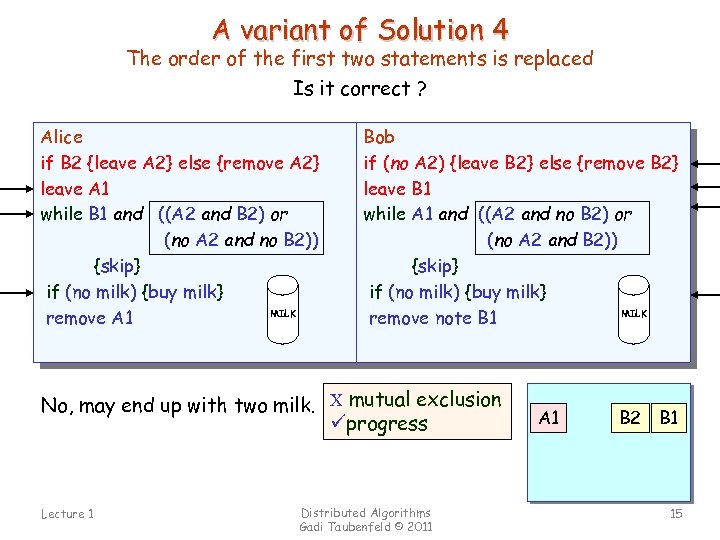
A variant of Solution 4 The order of the first two statements is replaced Is it correct ? Alice if B 2 {leave A 2} else {remove A 2} leave A 1 while B 1 and ((A 2 and B 2) or (no A 2 and no B 2)) {skip} if (no milk) {buy milk} MILK remove A 1 Bob if (no A 2) {leave B 2} else {remove B 2} leave B 1 while A 1 and ((A 2 and no B 2) or (no A 2 and B 2)) {skip} if (no milk) {buy milk} MILK remove note B 1 No, may end up with two milk. C mutual exclusion üprogress Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 A 1 B 2 B 1 15

Question Alice and Bob have a daughter C, make it work for all the three of them. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 16

Question x is an atomic register, initially 0 Process A for i = 1 to 5 { x: =x+1 } 0 Process B for i = 1 to 5 { x: =x+1 } Q: What are all the possible values for x after both processes terminate? A: 2 through 10 inclusive. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 17
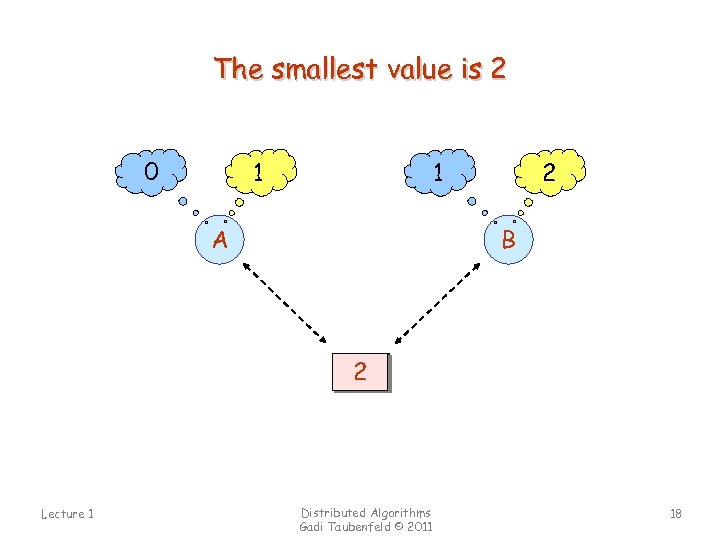
The smallest value is 2 0 1 1 0 A 2 1 B 2 5 4 3 0 1 Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 18

Question x is an atomic register, initially 0 Process A x: =x+1; x: =x+1 Process B x: =x+1; x: =x+1 0 Process C x: =10 Q: What are all the possible values for x after the three processes terminate? A: 2, 3, 4, 10, 11, 12, 13, 14. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 19
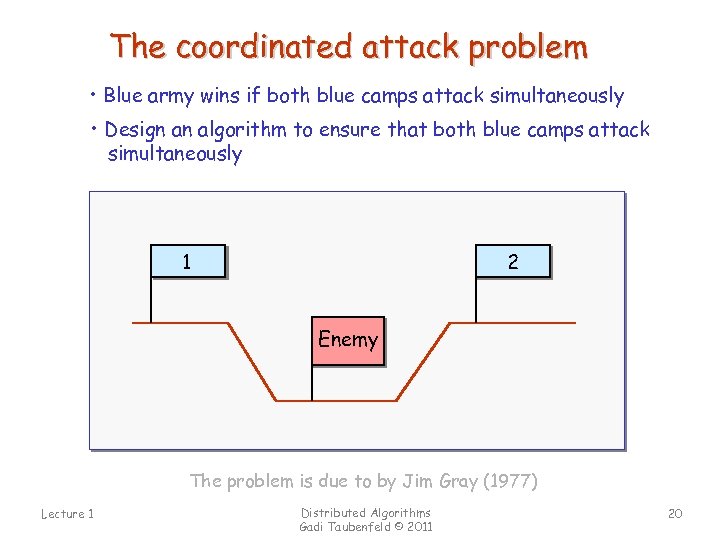
The coordinated attack problem • Blue army wins if both blue camps attack simultaneously • Design an algorithm to ensure that both blue camps attack simultaneously 1 2 Enemy The problem is due to by Jim Gray (1977) Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 20
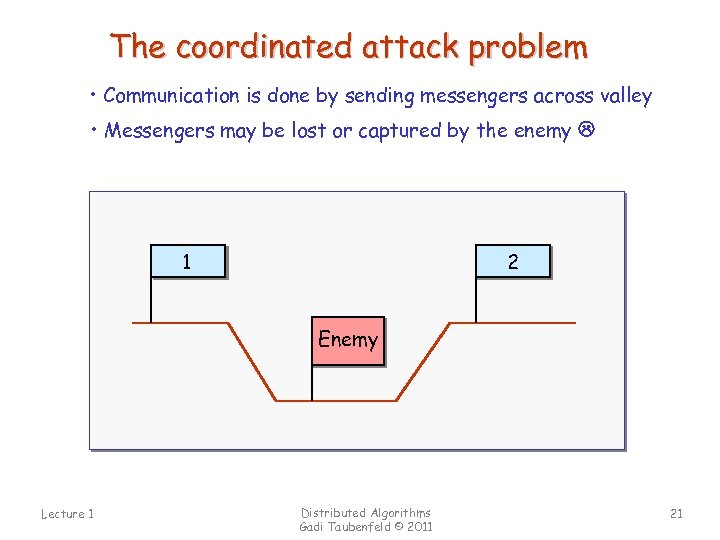
The coordinated attack problem • Communication is done by sending messengers across valley • Messengers may be lost or captured by the enemy 1 2 Enemy Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 21

The coordinated attack problem Theorem: There is no algorithm that solves the problem ! Proof: • Assume to the contrary that such an algorithm exits. • Let P be an algorithm that solves with fewest messages. • P should work even when the last messenger is captured. • So P should work even if the last messenger is never sent. • But this is a new algorithm with one less message. • A contradiction. The (asynchronous) model is too weak. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 22

Chapters 2+3 The mutual exclusion problem The first problem we cover in detail. A generalization of the too-much-milk problem. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 23
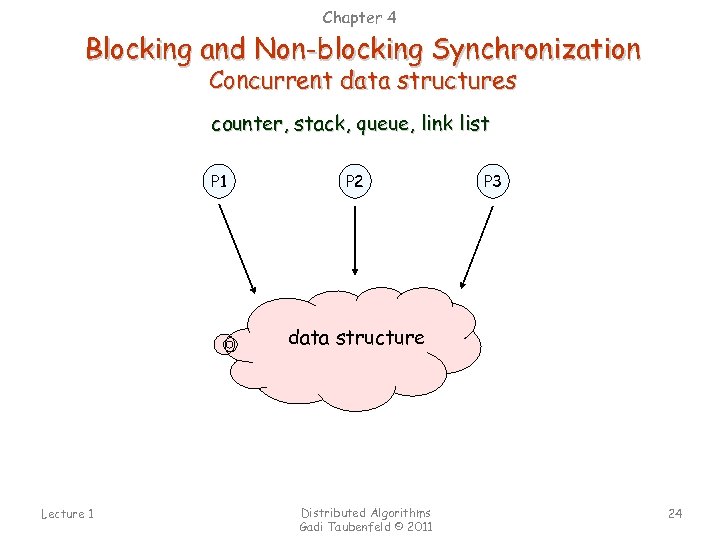
Chapter 4 Blocking and Non-blocking Synchronization Concurrent data structures counter, stack, queue, link list P 1 P 2 P 3 data structure Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 24
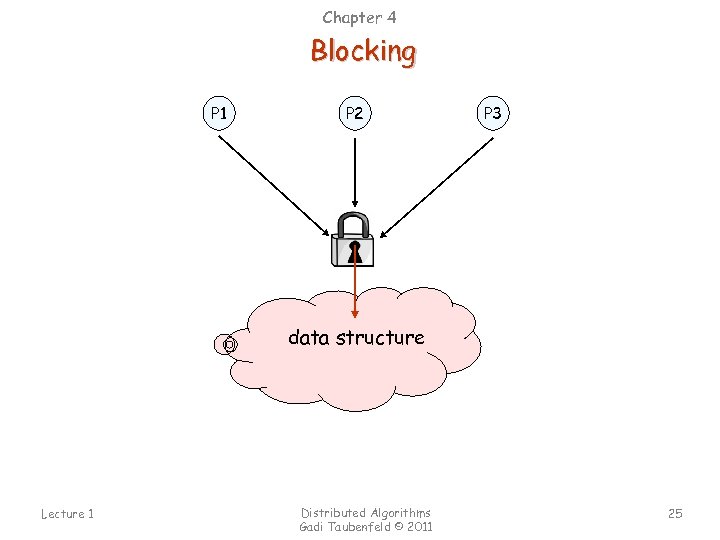
Chapter 4 Blocking P 1 P 2 P 3 data structure Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 25
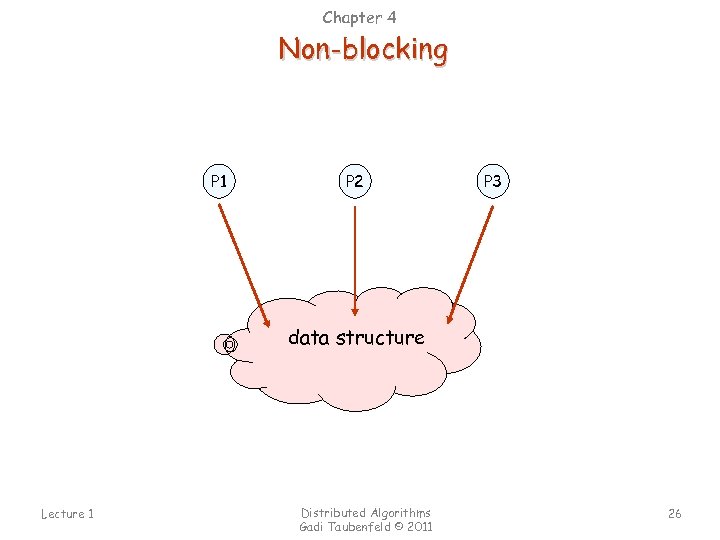
Chapter 4 Non-blocking P 1 P 2 P 3 data structure Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 26
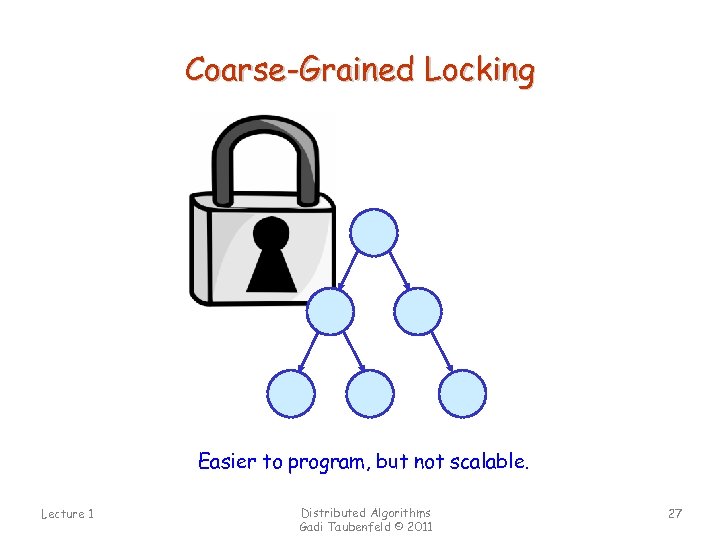
Coarse-Grained Locking Easier to program, but not scalable. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 27
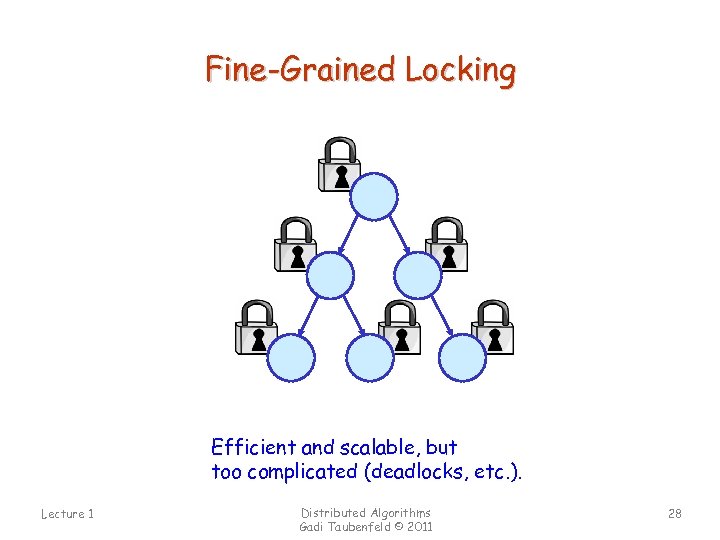
Fine-Grained Locking Efficient and scalable, but too complicated (deadlocks, etc. ). Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 28
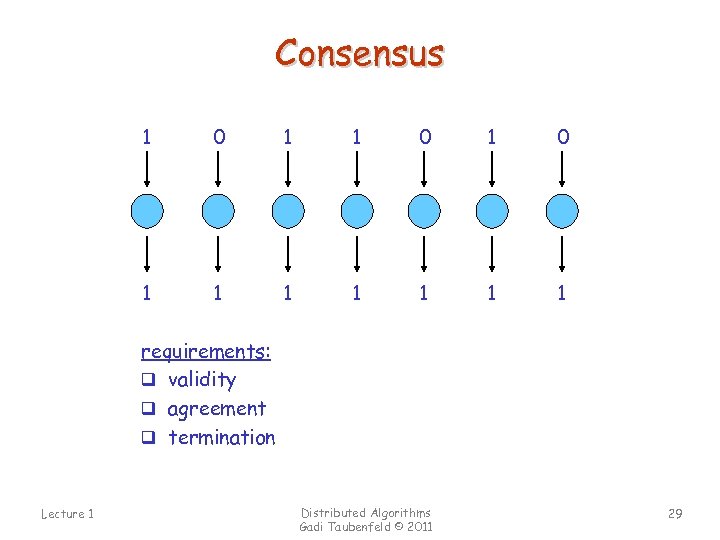
Consensus 1 0 1 0 1 1 1 1 requirements: q validity q agreement q termination Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 29

Impossibility of Consensus with One Faulty Process Theorem: There is no algorithm that solve the consensus problem using atomic read/write registers in the presence of a single faulty process. We give a detailed proof of this important result in Chapter 9 of the book. What can be done? q Strong primitives. q Timing assumptions. q Randomizations. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 30
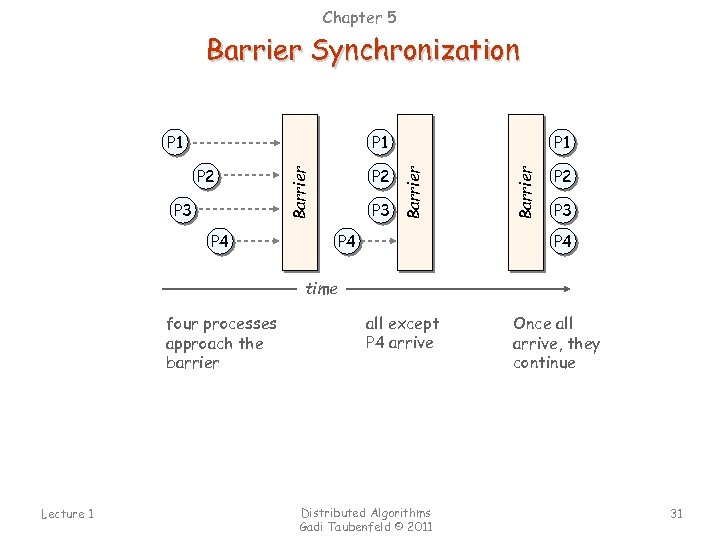
Chapter 5 Barrier Synchronization P 3 P 4 P 2 P 3 P 4 Barrier P 2 P 1 Barrier P 1 P 3 P 4 time four processes approach the barrier Lecture 1 all except P 4 arrive Distributed Algorithms Gadi Taubenfeld © 2011 Once all arrive, they continue 31
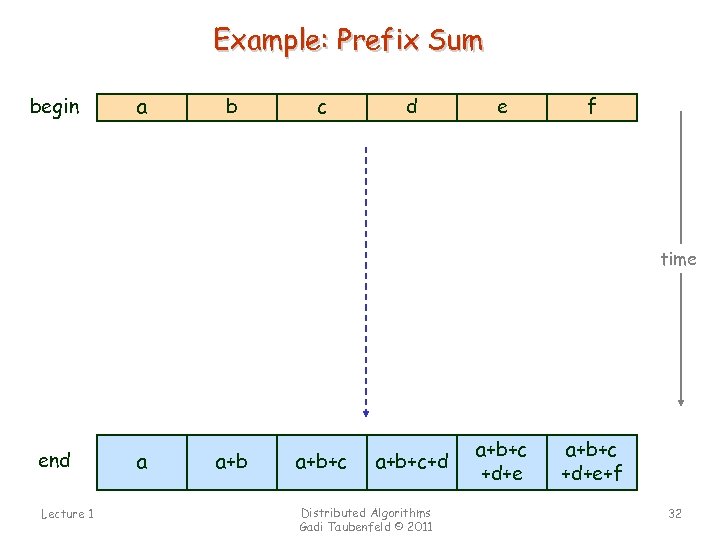
Example: Prefix Sum begin a b c d e f time end Lecture 1 a a+b+c+d Distributed Algorithms Gadi Taubenfeld © 2011 a+b+c +d+e+f 32
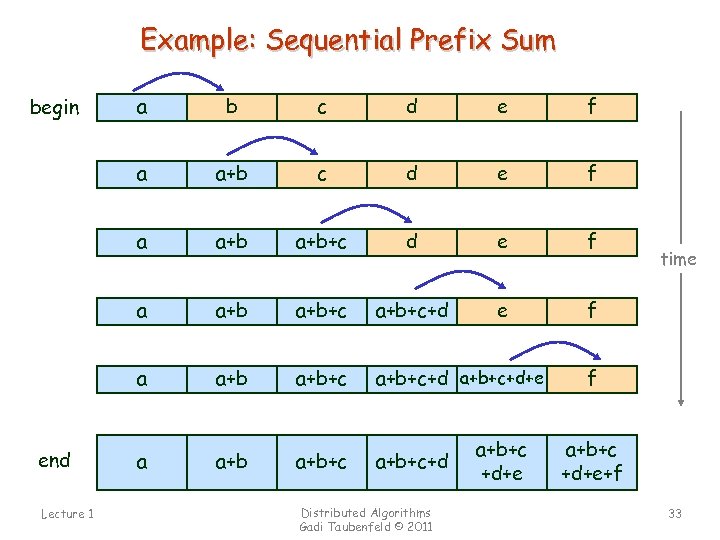
Example: Sequential Prefix Sum c d e f a+b a+b+c d e f a a+b+c+d e f a Lecture 1 b a end a a begin a+b+c+d+e a a+b+c+d Distributed Algorithms Gadi Taubenfeld © 2011 a+b+c +d+e time f a+b+c +d+e+f 33
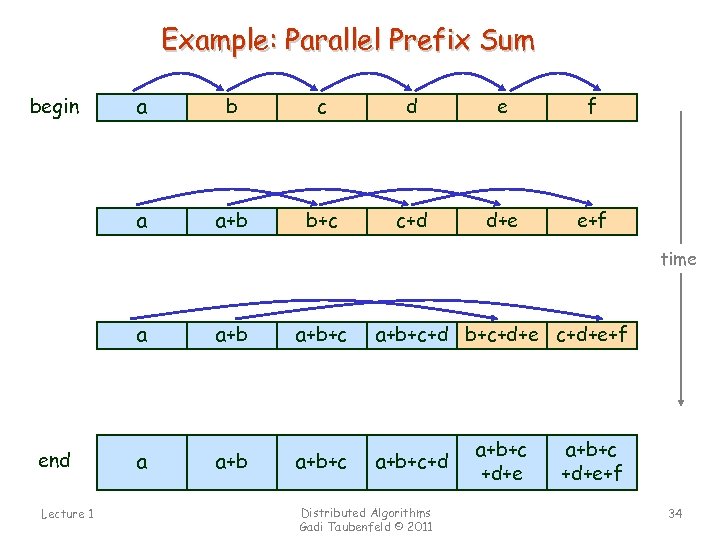
Example: Parallel Prefix Sum a b c d e f a begin a+b b+c c+d d+e e+f time a end Lecture 1 a+b+c+d b+c+d+e+f a a+b+c+d Distributed Algorithms Gadi Taubenfeld © 2011 a+b+c +d+e+f 34
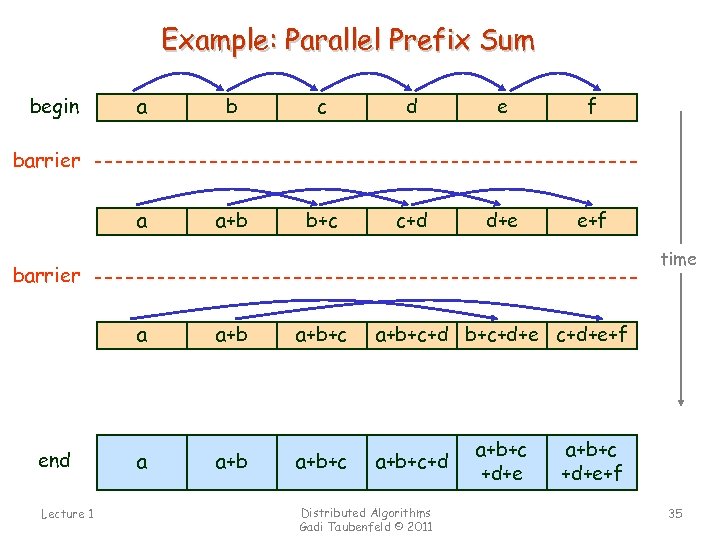
Example: Parallel Prefix Sum a b c d e f a begin a+b b+c c+d d+e e+f barrier time barrier a end Lecture 1 a+b+c+d b+c+d+e+f a a+b+c+d Distributed Algorithms Gadi Taubenfeld © 2011 a+b+c +d+e+f 35
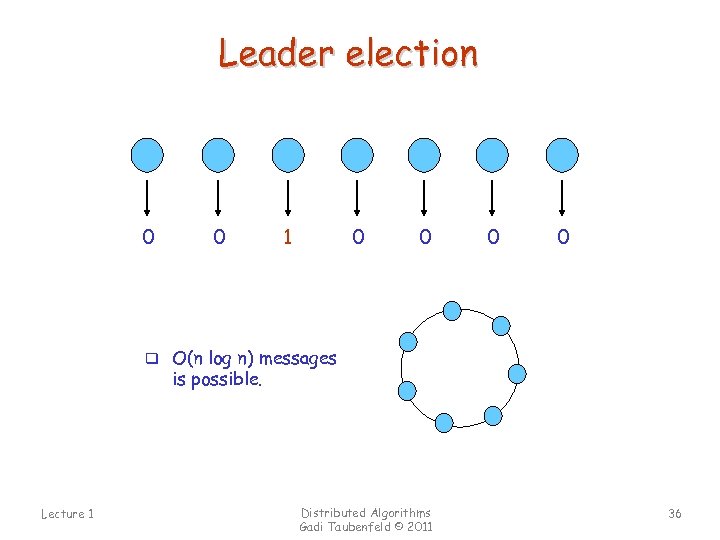
Leader election 0 0 1 0 0 q O(n log n) messages is possible. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 36
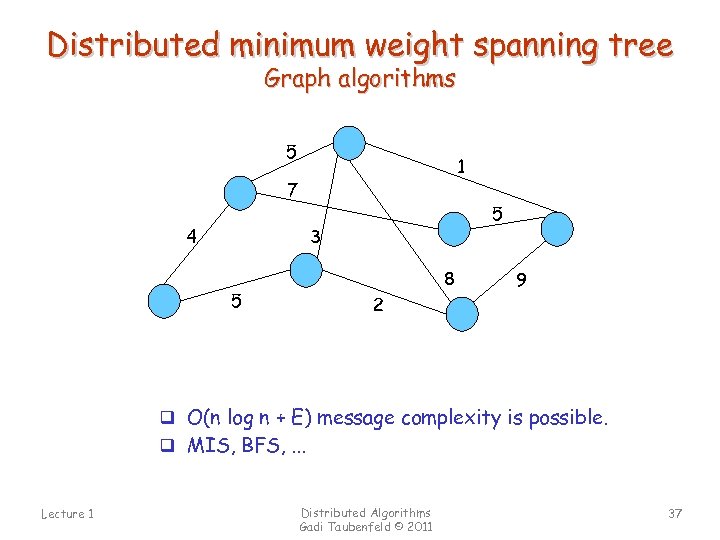
Distributed minimum weight spanning tree Graph algorithms 5 1 7 4 5 3 8 5 2 9 q O(n log n + E) message complexity is possible. q MIS, BFS, . . . Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 37
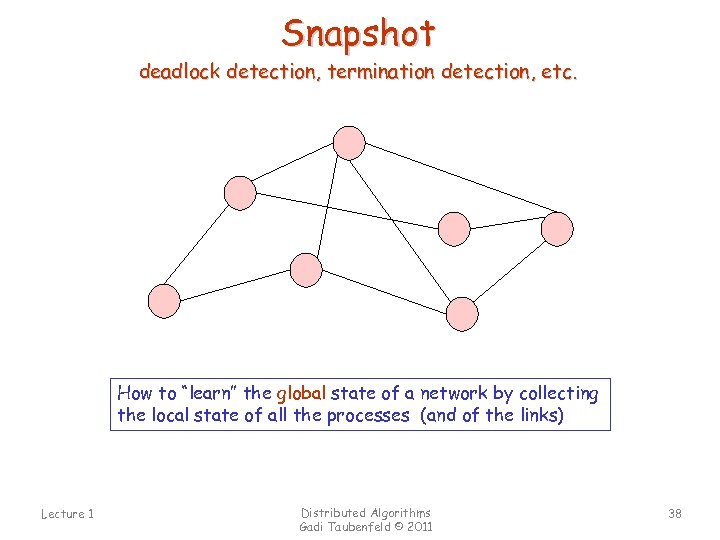
Snapshot deadlock detection, termination detection, etc. How to “learn” the global state of a network by collecting the local state of all the processes (and of the links) Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 38
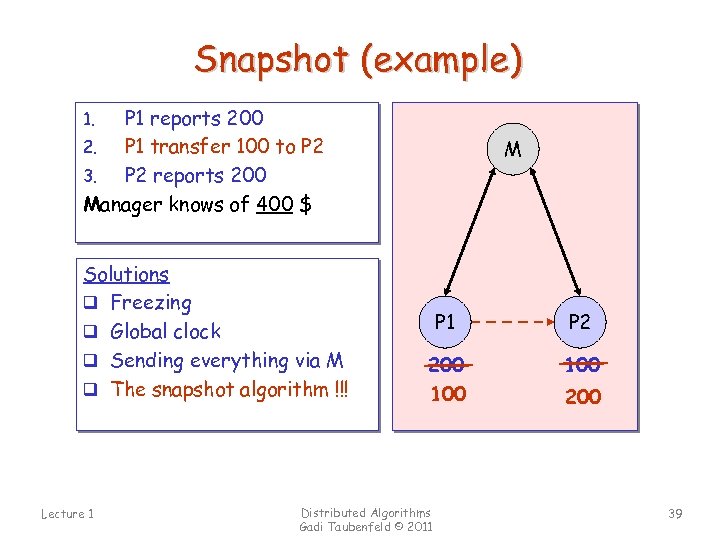
Snapshot (example) P 1 reports 200 2. P 1 transfer 100 to P 2 3. P 2 reports 200 Manager knows of 400 $ 1. Solutions q Freezing q Global clock q Sending everything via M q The snapshot algorithm !!! Lecture 1 M 100 P 1 200 100 Distributed Algorithms Gadi Taubenfeld © 2011 P 2 100 200 39
End-to-end communication sender Lecture 1 network Distributed Algorithms Gadi Taubenfeld © 2011 receiver 40
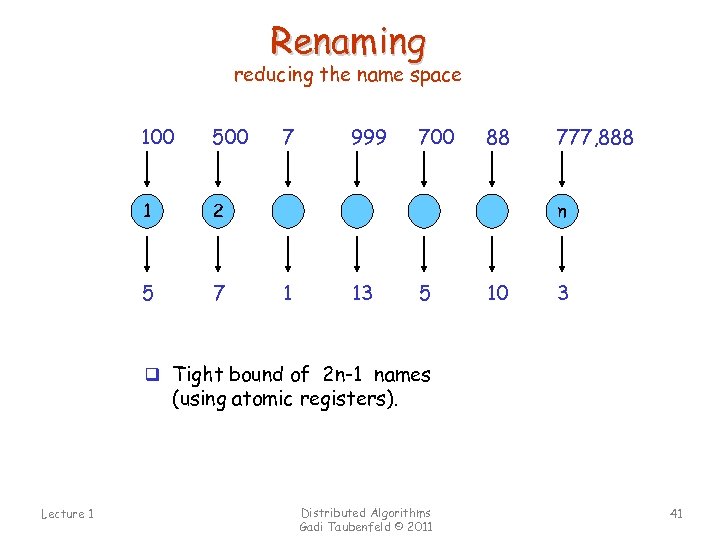
Renaming reducing the name space 100 500 1 2 5 7 7 999 700 88 777, 888 n 1 13 5 10 3 q Tight bound of 2 n-1 names (using atomic registers). Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 41

Clock synchronization (Data synchronization) The problem requires processors to bring their clocks close together, by using communication among them. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 42

Communication models of computation Concurrent programming Shared memory m m m m m safe registers atomic registers (read/write) test&set swap compare-and-swap load-link/store-conditional read-modify-write semaphore monitor What is the relative power of these communication primitives? Answer: see Chapter 9. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 43

Communication models of computation Message passing m m Lecture 1 send/receive multi-cast broadcast network topology Distributed Algorithms Gadi Taubenfeld © 2011 44
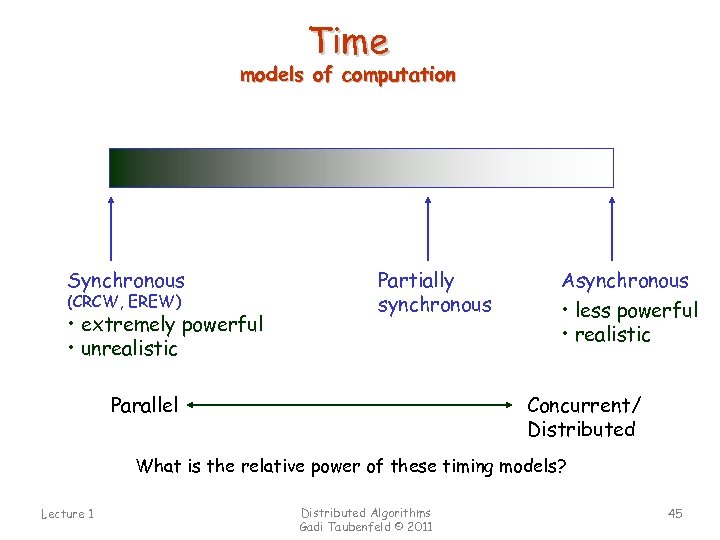
Time models of computation Synchronous (CRCW, EREW) • extremely powerful • unrealistic Partially synchronous Parallel Asynchronous • less powerful • realistic Concurrent/ Distributed What is the relative power of these timing models? Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 45

Fault-tolerance models of computation What can fail? m processes m shared memory m links Type of faults m crash m omission m Byzantine Lecture 1 How many can fail ? m constant, n/3, . . . Wait-freedom, Non-blocking, Lock-freedom m what is it ? Self-stabilization m what is it ? Distributed Algorithms Gadi Taubenfeld © 2011 46

Terminology q Hardware Processors q Software m Threads, processes q Sometimes OK to confuse them, sometimes not. q Scheduler m In this course it is always ok to confuse between processes and threads. Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 47
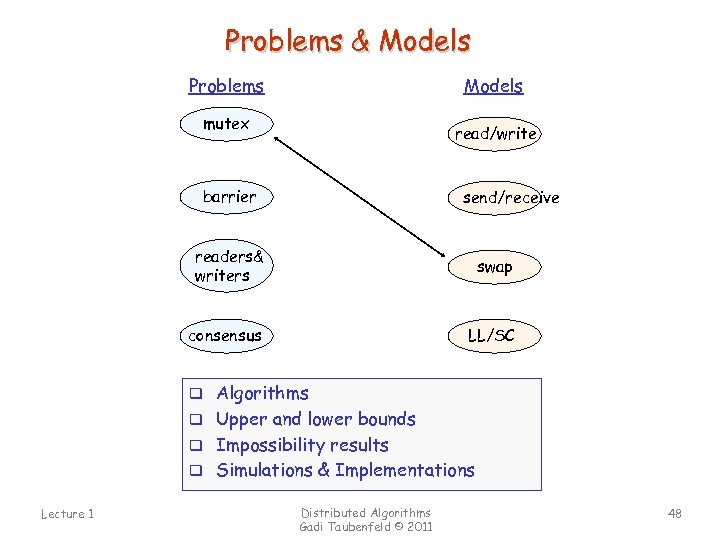
Problems & Models Problems Models mutex read/write barrier send/receive readers& writers swap consensus LL/SC q Algorithms q Upper and lower bounds q Impossibility results q Simulations & Implementations Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 48

History of the mutex problem q 1965 Defined by Dijkstra m First solution by Dekker m General solution by Dijkstra Fischer, Knuth, Lynch, Rabin, Rivest, . . . 1974 Lamport’s bakery algorithm 1981 Peterson’s solution There are hundreds of published solutions Lots or related problems m q q E. W. Dijkstra www. cs. utexas. edu/users/EWD/q (Photo by Hamilton Richards 2002) Lecture 1 Distributed Algorithms Gadi Taubenfeld © 2011 49
3c3b7f936fb5066a13e66f6964bb5742.ppt