Learning Rules from Data Olcay Taner Yıldız Ethem

Learning Rules from Data Olcay Taner Yıldız, Ethem Alpaydın yildizol@cmpe. boun. edu. tr Department of Computer Engineering Boğaziçi University

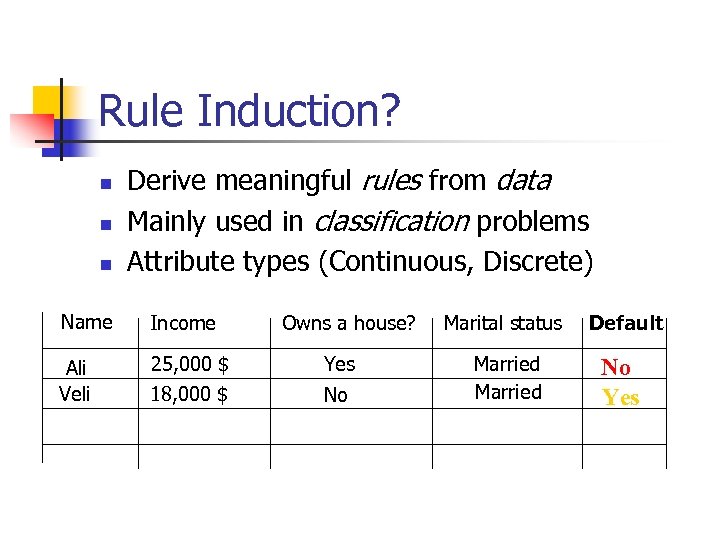Rule Induction? n n n Derive meaningful rules from data Mainly used in classification problems Attribute types (Continuous, Discrete) Name Income Ali Veli 25, 000 $ 18, 000 $ Owns a house? Yes No Marital status Default Married No Yes

Rules n n n Disjunction: conjunctions are binded via OR's Conjunction: propositions are binded via AND's Proposition: relation on an attribute n n Attribute is Continuous (defines a subinterval) Attribute is Discrete (= one of the values of the attribute)

How to generate rules? n Rule Induction Techniques n Via Trees n n C 4. 5 Rules Directly from Data n Ripper

C 4. 5 Rules (Quinlan, 93) n n Create decision tree using C 4. 5 Convert the decision tree to a ruleset by writing each path from root to the leaves as a rule

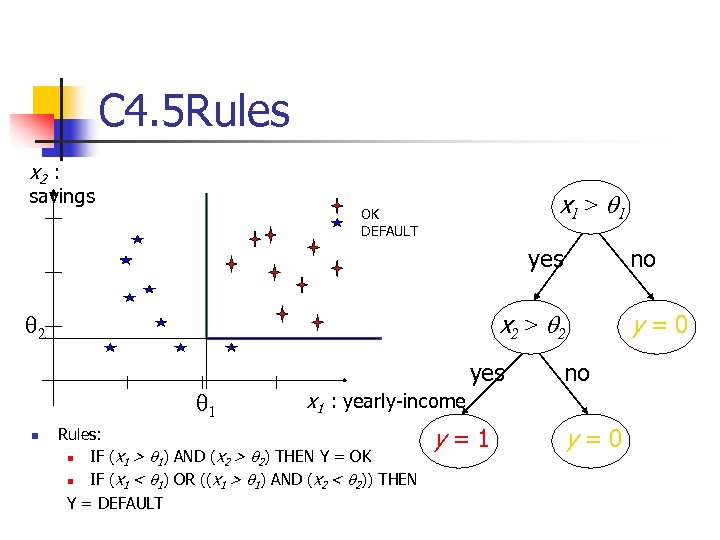C 4. 5 Rules x 2 : savings x 1 > q 1 OK DEFAULT yes x 2 > q 2 q 1 n no yes no x 1 : yearly-income Rules: n IF (x 1 > q 1) AND (x 2 > q 2) THEN Y = OK n IF (x 1 < q 1) OR ((x 1 > q 1) AND (x 2 < q 2)) THEN Y = DEFAULT y=1 y=0

RIPPER (Cohen, 95) n Learn rule for each class n n Objective class is positive, other classes are negative Two Steps n Initialization n Learn rules one by one Immediately prune learned rule Optimization n Since search is greeedy, pass k times over the rules to optimize

RIPPER (Initialization) n n Split (pos, neg) into growset and pruneset Rule : = grow conjunction with growset n n n Rule : = prune conjunction with pruneset n n n Remove propositions IF (x 1 > q 1) AND (x 2 < q 3) THEN Y = OK If MDL < Best MDL + 64 n n Add propositions one by one IF (x 1 > q 1) AND (x 2 > q 2) AND (x 2 < q 3) THEN Y = OK Add conjunction Else n Break

Ripper (Optimization) n Repeat K times n For each rule n n n n IF (x 1 > q 1) AND (x 2 < q 3) THEN Y = OK Generate revisionrule by adding propositions IF (x 1 > q 1) AND (x 2 < q 3) AND (x 1 > q 3) THEN Y = OK Generate replacementrule by regrowing IF (x 1 > q 4) THEN Y = OK Compare current rule with revisionrule and replacementrule Take the best according to MDL

Minimum Description Length n Description Length of a Ruleset n Description Length of Rules n n S = ||k|| + k log 2 (n / k) + (n – k) log 2 (k / (n – k)) Description Length of Exceptions n S = log 2 (|D| + 1) + fp (-log 2 (e / 2 C)) + (C – fp) (-log 2 (1 - e / 2 C)) + fn (-log 2 (fn / 2 U)) + (U – fn) (-log 2 (1 - fn / 2 U))

Ripper* n n Finding best condition is done by trying all possible split points (time-consuming) Shortcut: Linear Discriminant Analysis Split point is calculated analytically To be more robust n n Instances further than 3 are removed If number of examples < 20, shortcut not used

Experiments n n n 29 datasets from UCI repository are used 10 fold cross-validation Comparison done using one-sided t test Comparison of three algorithms C 4. 5 Rules, Ripper* Comparison based on n Error Rate Complexity of the rulesets Learning Time

Error Rate (I) n n n Ripper and its variant have better performance than C 4. 5 Rules Ripper* has similar performance compared to Ripper C 4. 5 Rules has advantage when the number of rules are small (Exhaustive Search)

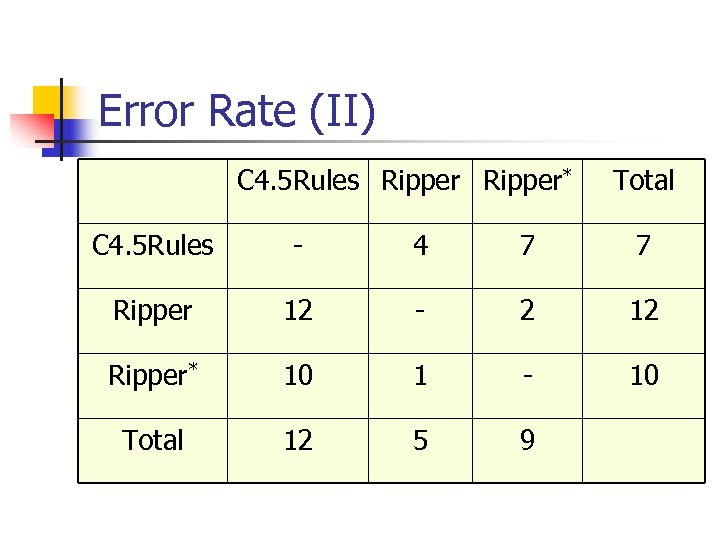Error Rate (II) C 4. 5 Rules Ripper* Total C 4. 5 Rules - 4 7 7 Ripper 12 - 2 12 Ripper* 10 1 - 10 Total 12 5 9

Ruleset Complexity (I) n n Ripper and Ripper* produce significantly small number of rules compared to C 4. 5 Rules starts with an unpruned tree, which is a large amount of rule to start

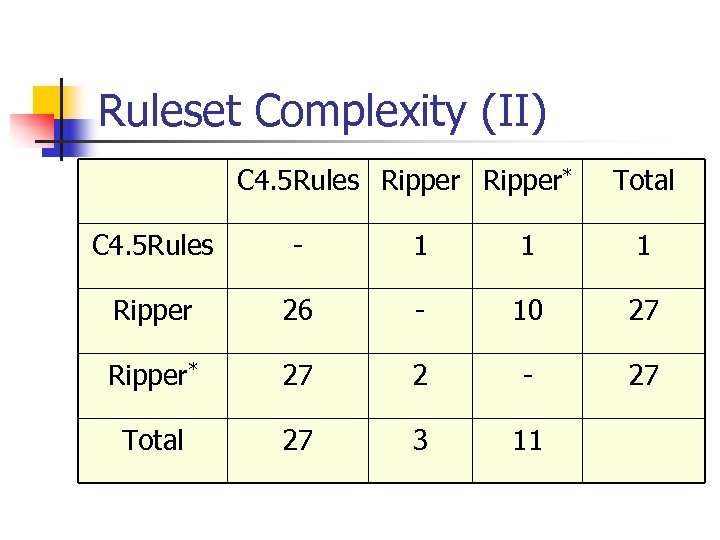Ruleset Complexity (II) C 4. 5 Rules Ripper* Total C 4. 5 Rules - 1 1 1 Ripper 26 - 10 27 Ripper* 27 2 - 27 Total 27 3 11

Learning Time (I) n n Ripper* better than Ripper, which is better than C 4. 5 Rules O(N 3) Ripper O(Nlog 2 N) Ripper* O(Nlog. N)

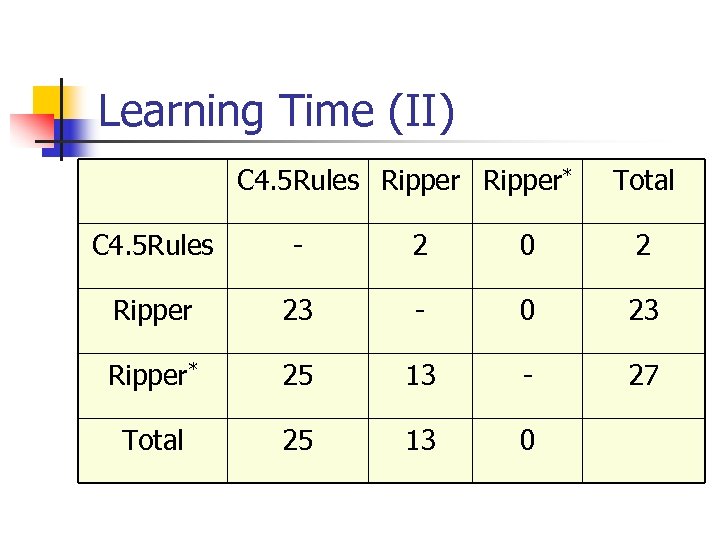Learning Time (II) C 4. 5 Rules Ripper* Total C 4. 5 Rules - 2 0 2 Ripper 23 - 0 23 Ripper* 25 13 - 27 Total 25 13 0

Conclusion n n Comparison of two rule induction algorithms C 4. 5 Rules and Ripper Proposed a shortcut in learning conditions using LDA (Ripper*) Ripper is better than C 4. 5 Rules Ripper* improves learning time of Ripper without decreasing its performance