48226bfc6c5560c9bb3a03d0f6417b4d.ppt
- Количество слайдов: 20

Learning Objectives for Section 14. 2 Applications in Business/Economics 1. The student will be able to construct and interpret probability density functions. 2, The student will be able to evaluate a continuous income stream. 3. The student will be able to evaluate consumers’ and producers’ surplus. Barnett/Ziegler/Byleen Business Calculus 11 e 1

Probability Density Functions A probability density function must satisfy: 1. f (x) 0 for all x 2. The area under the graph of f (x) is 1 3. If [c, d] is a subinterval then Probability (c x d) = Barnett/Ziegler/Byleen Business Calculus 11 e 2
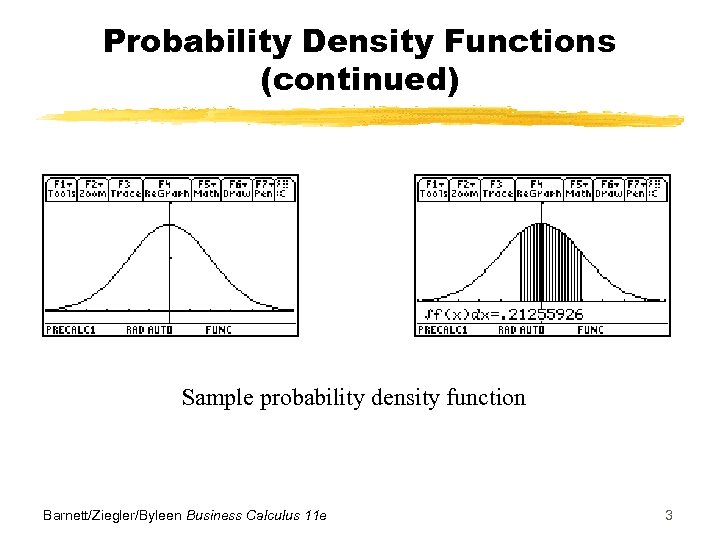
Probability Density Functions (continued) Sample probability density function Barnett/Ziegler/Byleen Business Calculus 11 e 3

Example In a certain city, the daily use of water in hundreds of gallons per household is a continuous random variable with probability density function Find the probability that a household chosen at random will use between 300 and 600 gallons. Barnett/Ziegler/Byleen Business Calculus 11 e 4

Insight The probability that a household in the previous example uses exactly 300 gallons is given by: In fact, for any continuous random variable x with probability density function f (x), the probability that x is exactly equal to a constant c is equal to 0. Barnett/Ziegler/Byleen Business Calculus 11 e 5
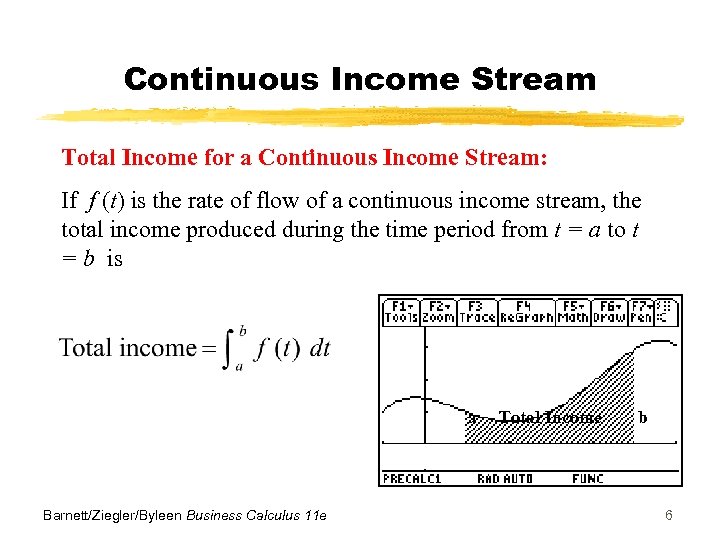
Continuous Income Stream Total Income for a Continuous Income Stream: If f (t) is the rate of flow of a continuous income stream, the total income produced during the time period from t = a to t = b is a Barnett/Ziegler/Byleen Business Calculus 11 e Total Income b 6

Example Find the total income produced by a continuous income stream in the first 2 years if the rate of flow is f (t) = 600 e 0. 06 t Barnett/Ziegler/Byleen Business Calculus 11 e 7

Example Find the total income produced by a continuous income stream in the first 2 years if the rate of flow is f (t) = 600 e 0. 06 t Barnett/Ziegler/Byleen Business Calculus 11 e 8

Future Value of a Continuous Income Stream From previous work we are familiar with the continuous compound interest formula A = Pert. If f (t) is the rate of flow of a continuous income stream, 0 t T, and if the income is continuously invested at a rate r compounded continuously, the future value FV at the end of T years is given by Barnett/Ziegler/Byleen Business Calculus 11 e 9

Example Let’s continue the previous example where f (t) = 600 e 0. 06 t Find the future value in 2 years at a rate of 10%. Barnett/Ziegler/Byleen Business Calculus 11 e 10

Example Let’s continue the previous example where f (t) = 600 e 0. 06 t Find the future value in 2 years at a rate of 10%. r = 0. 10, T = 2, f (t) = 600 e 0. 06 t Barnett/Ziegler/Byleen Business Calculus 11 e 11
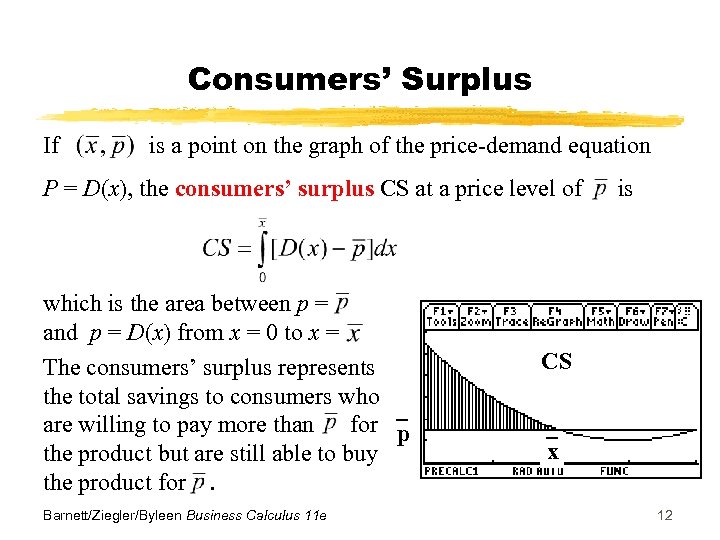
Consumers’ Surplus If is a point on the graph of the price-demand equation P = D(x), the consumers’ surplus CS at a price level of which is the area between p = and p = D(x) from x = 0 to x = The consumers’ surplus represents the total savings to consumers who are willing to pay more than for p the product but are still able to buy the product for. Barnett/Ziegler/Byleen Business Calculus 11 e is CS x 12

Example Find the consumers’ surplus at a price level of for the price-demand equation p = D (x) = 200 – 0. 02 x Barnett/Ziegler/Byleen Business Calculus 11 e 13

Example Find the consumers’ surplus at a price level of for the price-demand equation p = D (x) = 200 – 0. 02 x Step 1. Find the demand when the price is Barnett/Ziegler/Byleen Business Calculus 11 e 14

Example (continued) Step 2. Find the consumers’ surplus: Barnett/Ziegler/Byleen Business Calculus 11 e 15
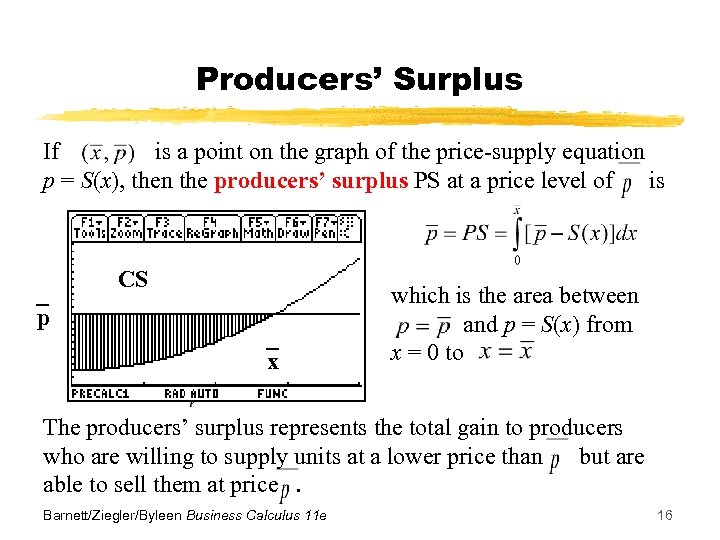
Producers’ Surplus If is a point on the graph of the price-supply equation p = S(x), then the producers’ surplus PS at a price level of is CS p x which is the area between and p = S(x) from x = 0 to The producers’ surplus represents the total gain to producers who are willing to supply units at a lower price than but are able to sell them at price. Barnett/Ziegler/Byleen Business Calculus 11 e 16

Example Find the producers’ surplus at a price level of for the price-supply equation p = S(x) = 15 + 0. 1 x + 0. 003 2 Barnett/Ziegler/Byleen Business Calculus 11 e 17

Example Find the producers’ surplus at a price level of for the price-supply equation p = S(x) = 15 + 0. 1 x + 0. 003 x 2 Step 1. Find , the supply when the price is Solving for using a graphing utility: Barnett/Ziegler/Byleen Business Calculus 11 e 18

Example (continued) Step 2. Find the producers’ surplus: Barnett/Ziegler/Byleen Business Calculus 11 e 19

Summary ■ ■ ■ We learned how to use a probability density function. We defined and used a continuous income stream. We found the future value of a continuous income stream. We defined and calculated a consumer’s surplus. We defined and calculated a producer’s surplus. Barnett/Ziegler/Byleen Business Calculus 11 e 20
48226bfc6c5560c9bb3a03d0f6417b4d.ppt