Learning Hypernetworks by Random Graph Processes Byoung-Tak Zhang

Learning Hypernetworks by Random Graph Processes Byoung-Tak Zhang Partially Based on SNU CSE Lecture Notes on Biomolecular Computation Spring 2003

Outline l Random Graph Process (RGP) …………… 3 ¨ An Example ¨ Reaction Graphs l Random Hypergraphs ………………. . 9 ¨ Space of Hypergraphs ¨ Learning Hypergraphs by RGP l Applications ……………………. 24 ¨ Image Recognition ¨ Sentence Generation l l FPGA Implementation ………………. 42 Conclusion ……………………… 46 2

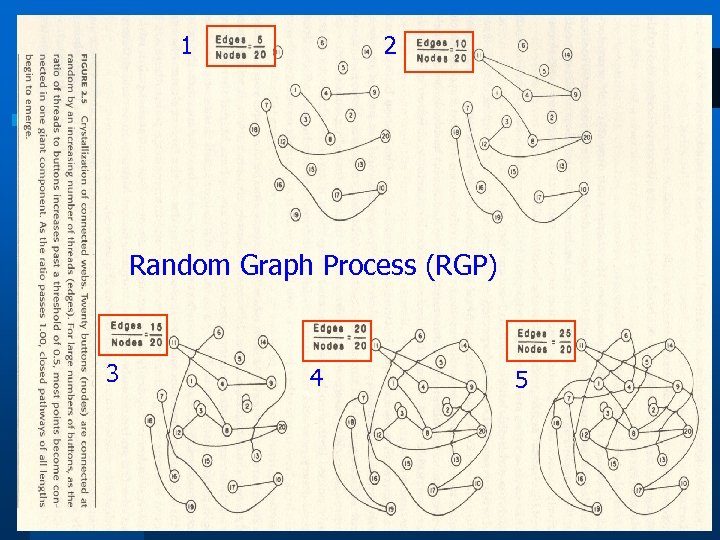
1 2 Random Graph Process (RGP) 3 4 5 3

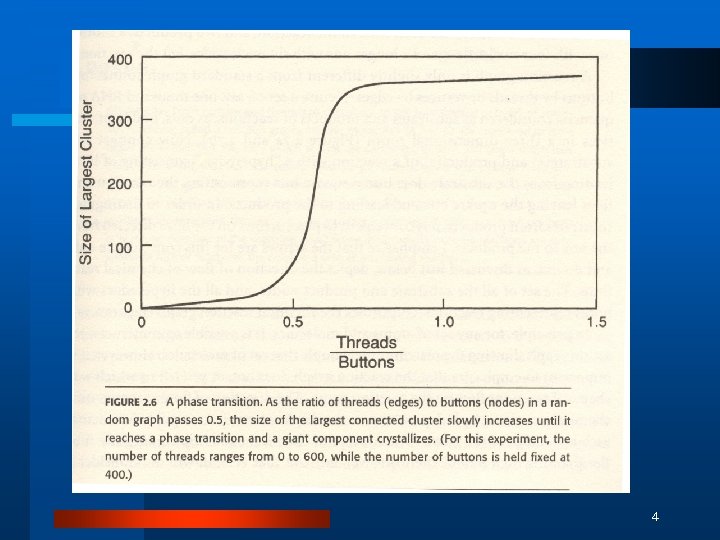
4

Collectively Autocatalytic Sets l “A contemporary cell is a collectively autocatalytic whole in which DNA, RNA, the code, proteins, and metabolism linking the synthesis of species of some molecular species to the breakdown of other “high-energy” molecular species all weave together and conspire to catalyze the entire set of reactions required for the whole cell to reproduce. ” (Kauffman) 5

Reaction Graph 6

7

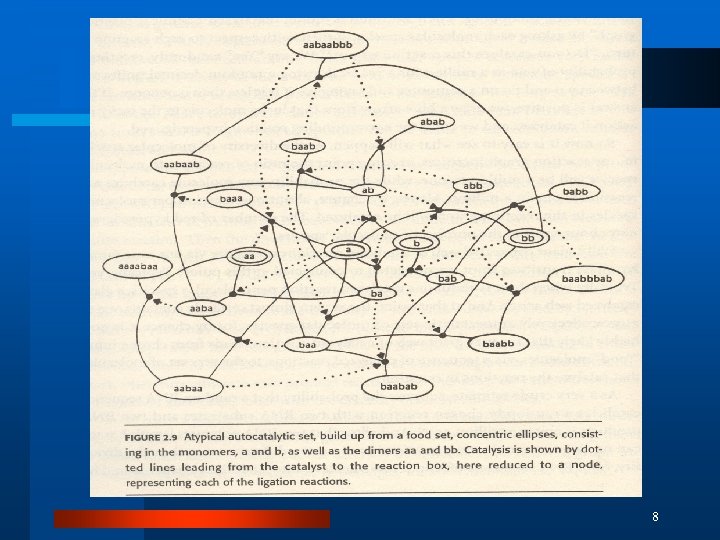
8

Random Hypergraphs

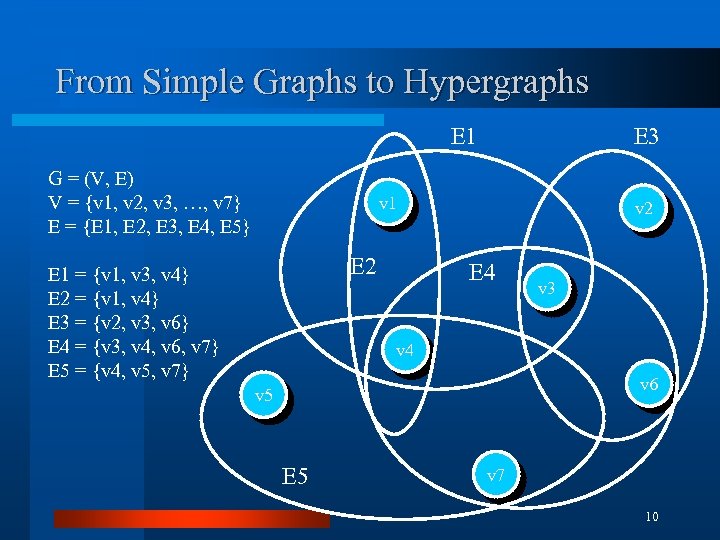
From Simple Graphs to Hypergraphs E 1 G = (V, E) V = {v 1, v 2, v 3, …, v 7} E = {E 1, E 2, E 3, E 4, E 5} E 3 v 1 E 2 E 1 = {v 1, v 3, v 4} E 2 = {v 1, v 4} E 3 = {v 2, v 3, v 6} E 4 = {v 3, v 4, v 6, v 7} E 5 = {v 4, v 5, v 7} v 2 E 4 v 3 v 4 v 6 v 5 E 5 v 7 10

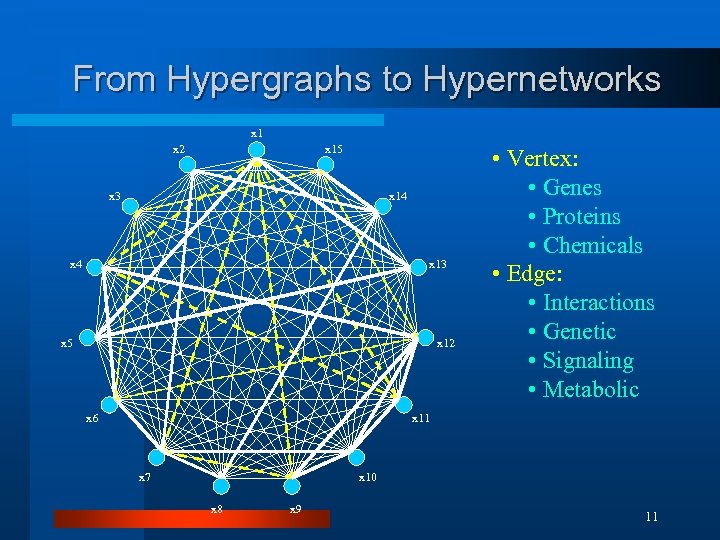
From Hypergraphs to Hypernetworks x 1 x 2 x 15 x 3 x 14 x 13 x 5 x 12 x 6 • Vertex: • Genes • Proteins • Chemicals • Edge: • Interactions • Genetic • Signaling • Metabolic x 11 x 7 x 10 x 8 x 9 11

Hypernetworks l l l [Zhang, DNA 12 -2006] A hypernetwork is a hypergraph of weighted edges. It is defined as a triple H = (V, E, W), where V = {v 1, v 2, …, vn}, E = {E 1, E 2, …, En}, and W = {w 1, w 2, …, wn}. An m-hypernetwork consists of a set V of vertices and a subset E of V[m], i. e. H = (V, V[m], W) where V[m] is a set of subsets of V whose elements have precisely m members and W is the set of weights associated with the hyperedges. A hypernetwork H is said to be k-uniform if every edge Ei in E has cardinality k. A hypernetwork H is k-regular if every vertex has degree k. Rem. : An ordinary graph is a 2 -uniform hypergraph with wi=1. 12

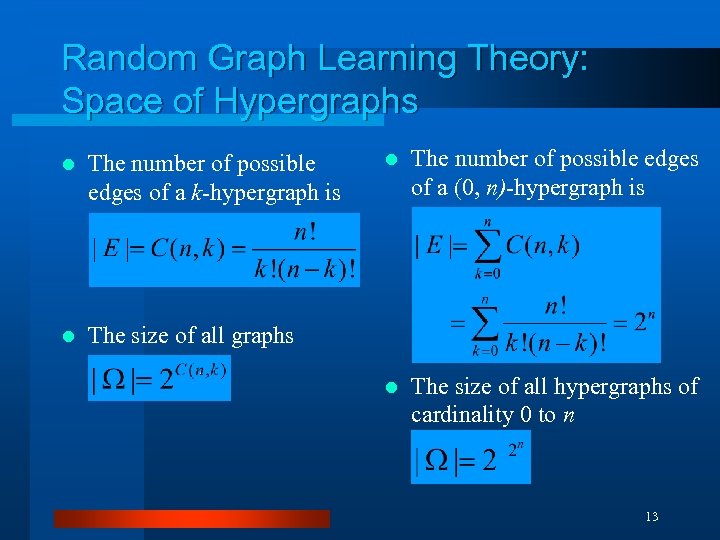
Random Graph Learning Theory: Space of Hypergraphs l The number of possible edges of a k-hypergraph is l l The number of possible edges of a (0, n)-hypergraph is l The size of all hypergraphs of cardinality 0 to n The size of all graphs 13

Random Graph Learning Theory: Probability Space l Probability space l Probability of a graph C(n, k) independent tosses of a fair coin, i. e. Bernoulle experiments 14

Random Hypergraph Process [Zhang, FOCI-2007] l Given p, the random hypergraphs can be generated by a binomial random graph process l Alternatively, given M, the random hypergraphs can be generated by a uniform random graph process 15

From Random Hypergraphs to Random Hypernets l The number of possible edges l The number of all graphs l The sampling method can be used for hypergraphs and hypernetworks. 16

Learning Hypergraphs by Random Graph Processes

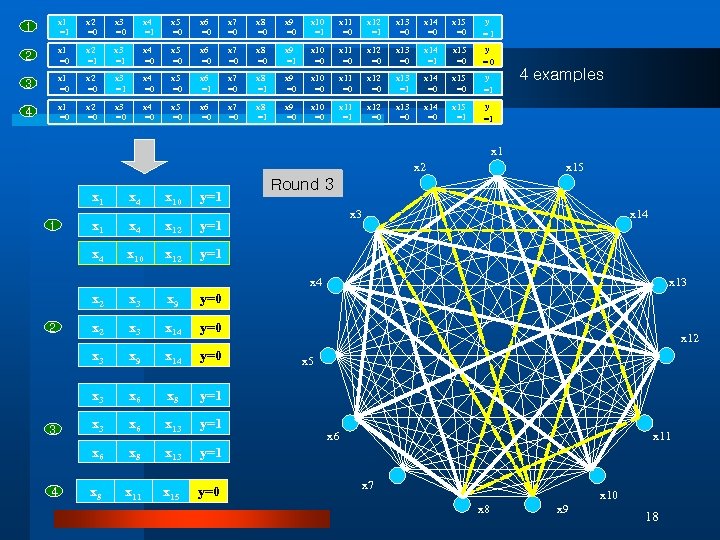
1 x 1 =1 x 2 =0 x 3 =0 x 4 =1 x 5 =0 x 6 =0 x 7 =0 x 8 =0 x 9 =0 x 10 =1 x 11 =0 x 12 =1 x 13 =0 x 14 =0 x 15 =0 y =1 2 x 1 =0 x 2 =1 x 3 =1 x 4 =0 x 5 =0 x 6 =0 x 7 =0 x 8 =0 x 9 =1 x 10 =0 x 11 =0 x 12 =0 x 13 =0 x 14 =1 x 15 =0 y =0 3 x 1 =0 x 2 =0 x 3 =1 x 4 =0 x 5 =0 x 6 =1 x 7 =0 x 8 =1 x 9 =0 x 10 =0 x 11 =0 x 12 =0 x 13 =1 x 14 =0 x 15 =0 y =1 4 x 1 =0 x 2 =0 x 3 =0 x 4 =0 x 5 =0 x 6 =0 x 7 =0 x 8 =1 x 9 =0 x 10 =0 x 11 =1 x 12 =0 x 13 =0 x 14 =0 x 15 =1 y =1 4 examples x 1 x 2 x 10 y=1 x 4 x 12 x 10 x 12 Round 1 3 2 y=1 x 4 x 15 y=1 x 3 x 14 x 2 x 3 x 14 y=0 x 9 x 14 y=0 x 6 x 8 y=1 x 3 x 6 x 13 y=1 x 6 4 y=0 x 3 3 x 9 x 3 2 x 3 x 8 x 13 y=1 x 8 x 11 x 15 y=0 x 13 x 12 x 5 x 6 x 11 x 7 x 10 x 8 x 9 18

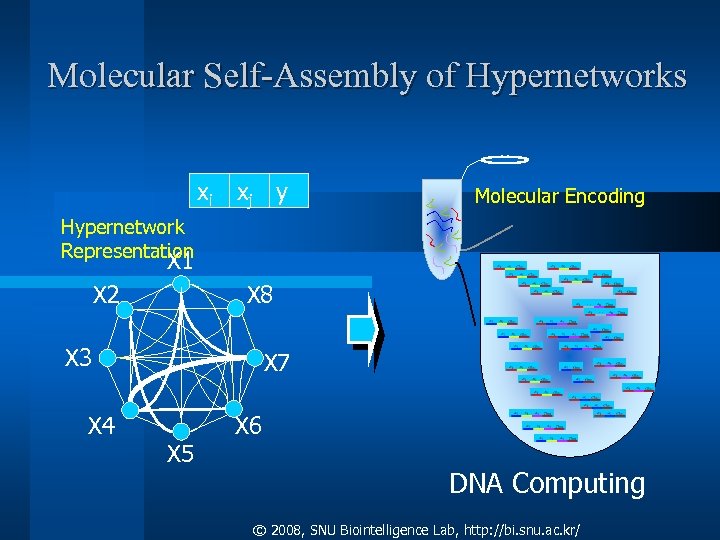
Molecular Self-Assembly of Hypernetworks xi xj y Molecular Encoding Hypernetwork Representation X 1 X

Random Hypergraph Process 1. Start with the initial hypernetwork 2. Get a training sample . Generate a hypernetwork as follows. - Generate hyperedges - x: may include the label y as a special attribute 3. 4. Go to step 2 if not terminated. 20

The Hypernetwork Model of Memory [Zhang, 2006] © 2007, SNU Biointelligence Lab, http: //bi.

Deriving the Learning Rule 22

Derivation of the Learning Rule 23

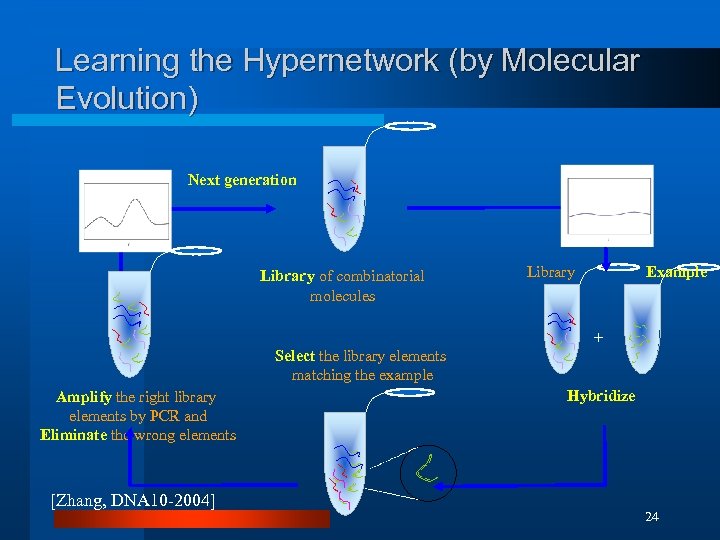
Learning the Hypernetwork (by Molecular Evolution) Next generation Library of combinatorial molecules Library Example + Select the library elements matching the example Amplify the right library elements by PCR and Eliminate the wrong elements [Zhang, DNA 10 -2004] Hybridize 24

Image Recognition

Digit Recognition: Data Set l Original Data ¨ Handwritten digits (0 ~ 9) ¨ Training data: 2, 630 (263 examples for each class) ¨ Test data: 1, 130 (113 examples for each class) l Preprocessing ¨ Each example is 8 x 8 binary matrix. ¨ Each pixel is 0 or 1. 26

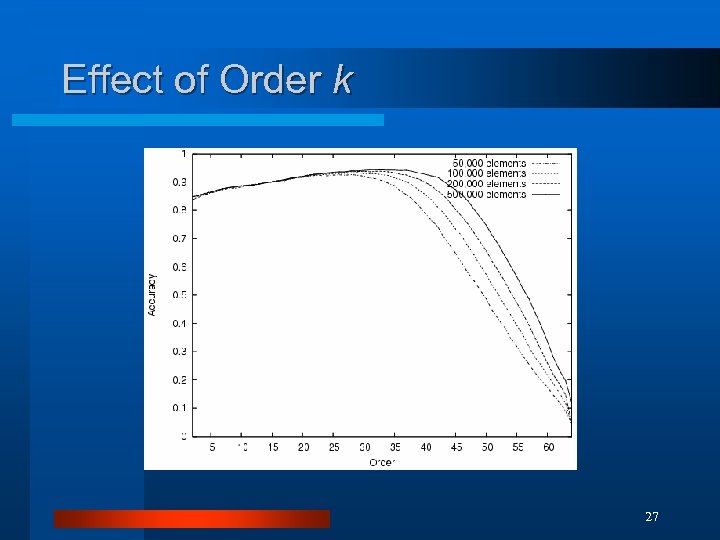
Effect of Order k 27

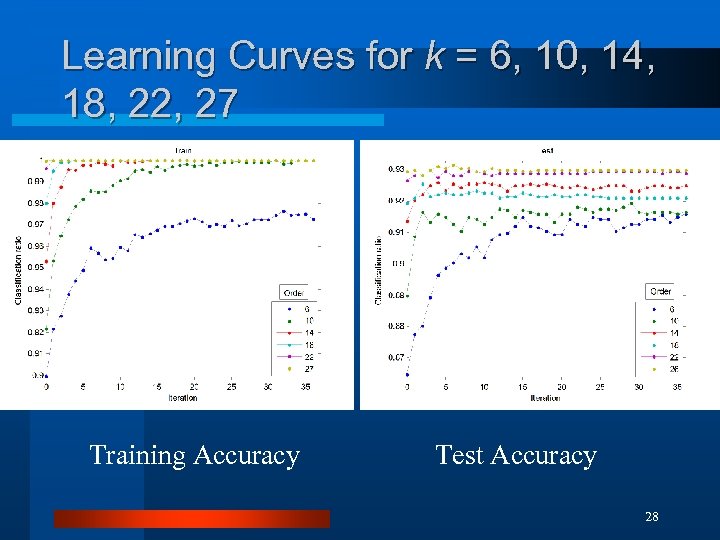
Learning Curves for k = 6, 10, 14, 18, 22, 27 Training Accuracy Test Accuracy 28

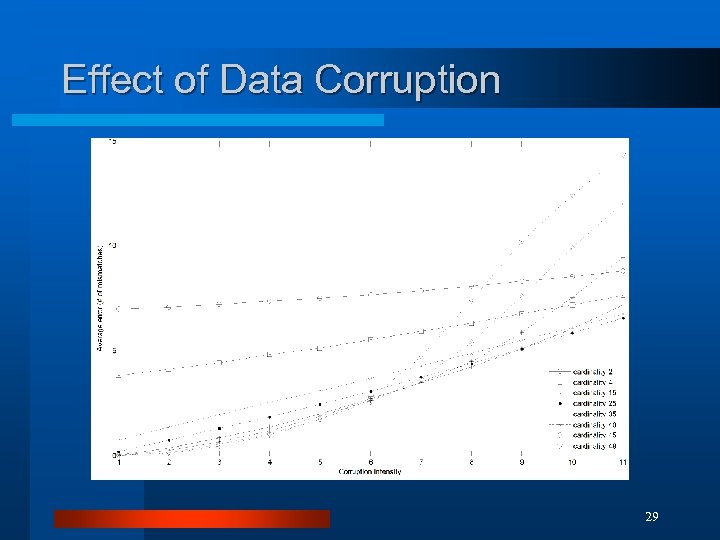
Effect of Data Corruption 29

Face Data Set Yale dataset l 15 people l 11 images person l Total 165 images l 30

Bitmaps for Training Data (Dimensionality = 480) 31

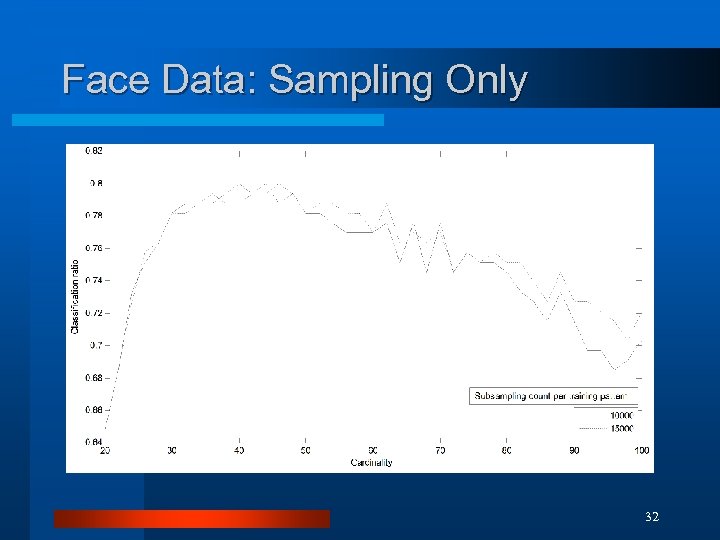
Face Data: Sampling Only 32

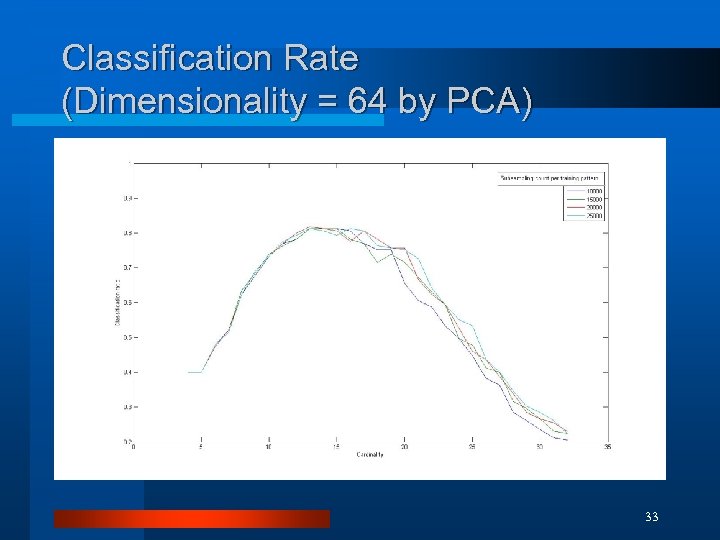
Classification Rate (Dimensionality = 64 by PCA) 33

Image Classification: Data Sets bikes cars persons § Example of objects of Graz 01 dataset: four images of the categories bike, car, person 34

Sampling Strategies [Nowak et al, ECCV 2006] § Examples of multi-scale sampling methods Harris-Laplace (HL) with a large detection threshold Laplacian-of-Gaussian (LOG) HL with threshold zero – note that the sampling is still quite sparse. Random sampling 35

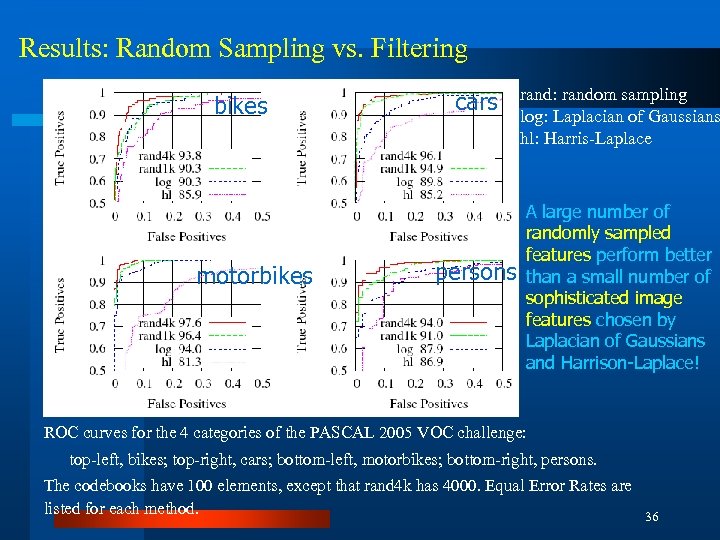
Results: Random Sampling vs. Filtering bikes motorbikes cars persons rand: random sampling log: Laplacian of Gaussians hl: Harris-Laplace A large number of randomly sampled features perform better than a small number of sophisticated image features chosen by Laplacian of Gaussians and Harrison-Laplace! ROC curves for the 4 categories of the PASCAL 2005 VOC challenge: top-left, bikes; top-right, cars; bottom-left, motorbikes; bottom-right, persons. The codebooks have 100 elements, except that rand 4 k has 4000. Equal Error Rates are listed for each method. 36

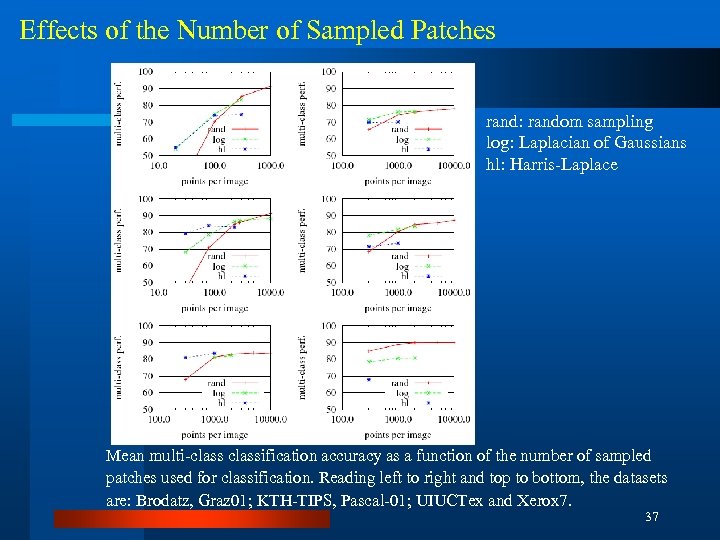
Effects of the Number of Sampled Patches rand: random sampling log: Laplacian of Gaussians hl: Harris-Laplace Mean multi-classification accuracy as a function of the number of sampled patches used for classification. Reading left to right and top to bottom, the datasets are: Brodatz, Graz 01; KTH-TIPS, Pascal-01; UIUCTex and Xerox 7. 37

Sentence Generation

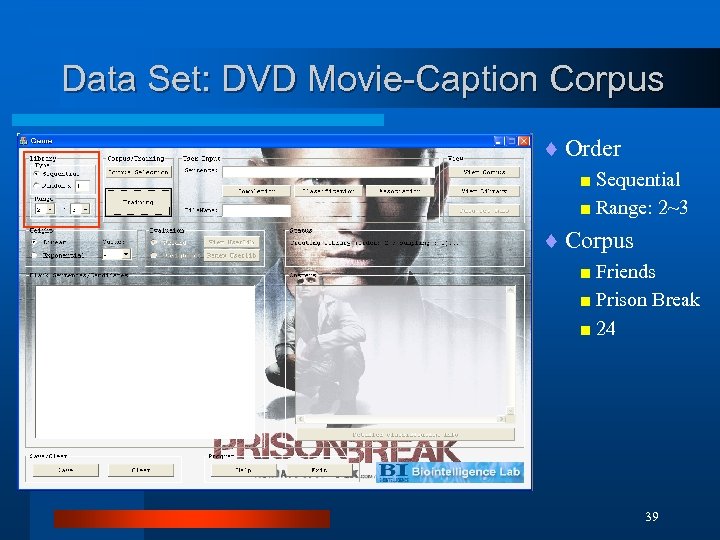
Data Set: DVD Movie-Caption Corpus ¨ Order < Sequential < Range: 2~3 ¨ Corpus < Friends < Prison Break < 24 39

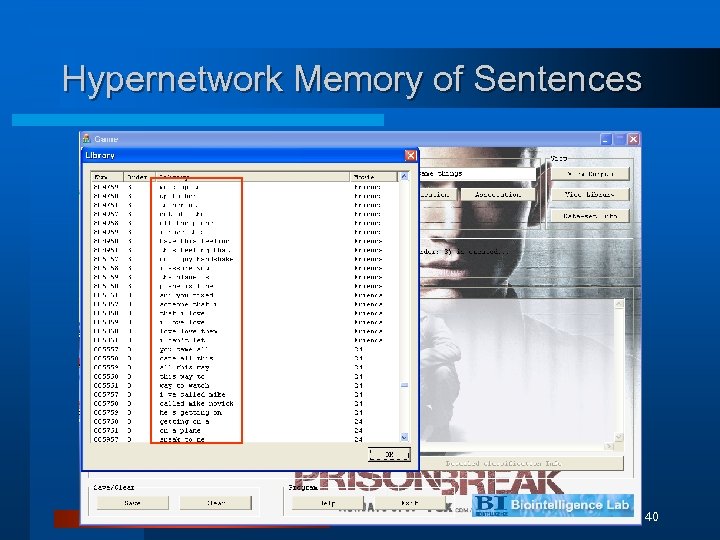
Hypernetwork Memory of Sentences 40

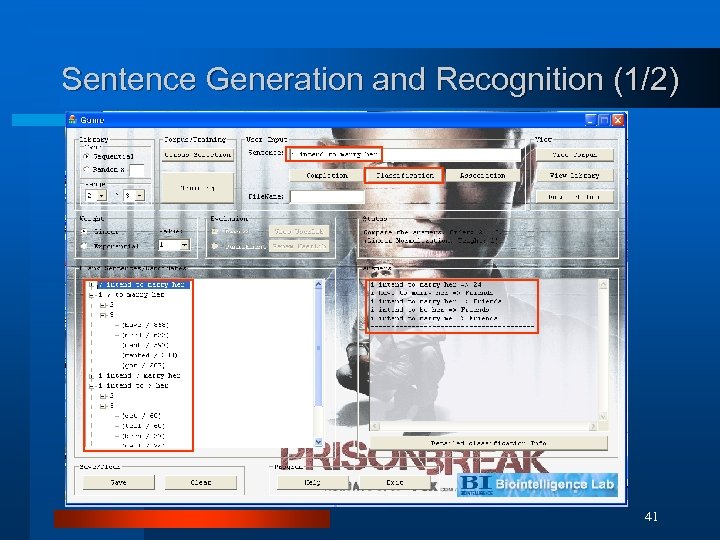
Sentence Generation and Recognition (1/2) 41

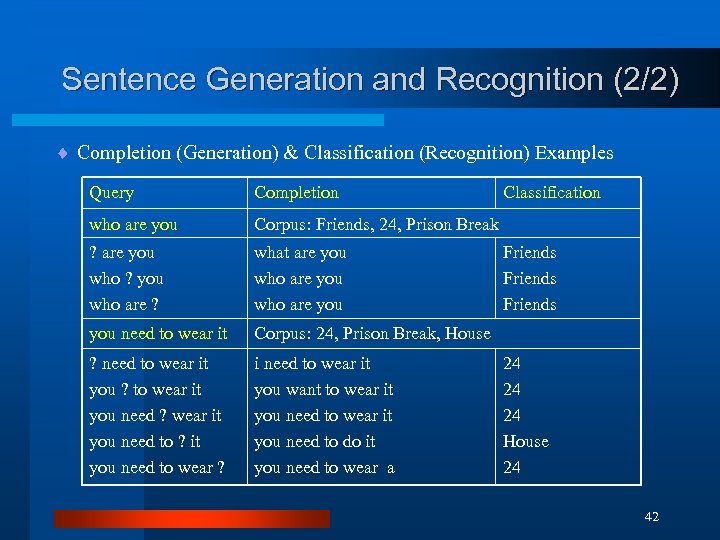
Sentence Generation and Recognition (2/2) ¨ Completion (Generation) & Classification (Recognition) Examples Query Completion who are you Corpus: Friends, 24, Prison Break ? are you who ? you who are ? what are you who are you need to wear it Corpus: 24, Prison Break, House ? need to wear it you ? to wear it you need ? wear it you need to ? it you need to wear ? i need to wear it you want to wear it you need to do it you need to wear a Classification Friends 24 24 24 House 24 42

FPGA Implementation

FPGA Implementation [JKKim et al. , DNA-2007] [JKKim et al. , 2007, in preparation] In collaboration with Inha Univ. 44

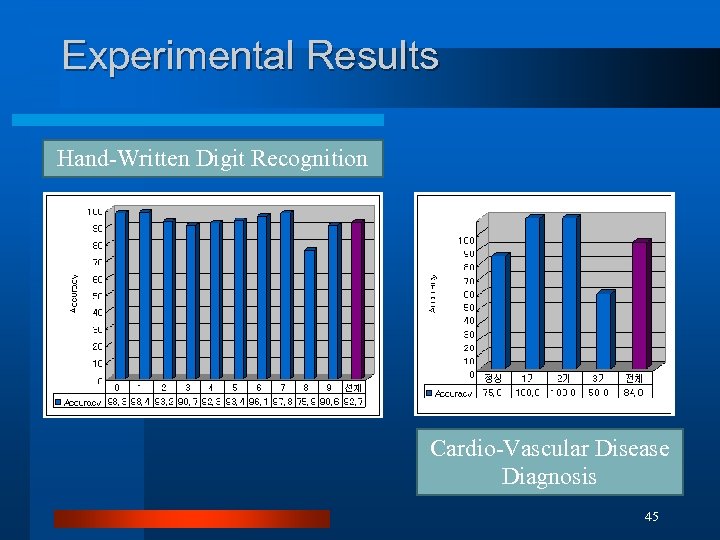
Experimental Results Hand-Written Digit Recognition Cardio-Vascular Disease Diagnosis 45

Promising Application Areas l Stream Data: 학습 데이터가 스트림으로 연속적으로 들어오는 문제 ¨ Video Analysis, UCC Data Analysis l Dynamic Environment: 학습의 목표가 시간에 따라 변화하는 환경 ¨ UI Agents, Dialog Systems l Massive-Scale Learning: 학습 데이터의 양이 너무 커서 모두 보존하 는 것이 불가능한 환경 ¨ Lifelong Camera, Visual Diary l Time Series Prediction: 시간적 변화의 트렌드를 파악하고 추적하는 문제 ¨ Targeting, Tracking l Detection and Discovery: 가끔 발생하는 특이한 상황을 예측하고 발 견하는 문제 ¨ Anomaly Detection 46

Conclusion The hypegraphs and hypernetworks are a useful structure to identify complex interactions among a large number of variables. l We propose to use random graph processes (RGPs) to learn pattern classifiers of hypernetwork structure. l The hypernetworks are successfully evolved to solve digit recognition, face recognition, and sentence recognition and generation problems. l The RGP-based learning algorithm was originally designed to be naturally implemented chemically (in vitro) using DNA computing technology, but it can also be easily implemented electronically (in silico) using CMOS memory technology. l 47