Learning How to Learn Mathematics Wade Ellis Jr

Learning How to Learn Mathematics Wade Ellis, Jr. West Valley College (retired) wade 25@sbcglobal. net

The Ability of Students to Learn We are all trying to improve student performance. We spend lots of time and effort on improving the material we present (textbooks, handouts) and our ability to present it using modern approaches. These efforts are valuable and should continue. However, we do not spend much time working on improving students’ ability or capacity to learn mathematics. That’s what I’d like to talk about today.

Introduction Outline – Jim Stigler: students need to be engaged in Productive Struggle, Explicit Connections, Deliberate Practice Learning is a Process Mathematics Classroom Culture – 14 Aspects Developmental Math Learning Risk Factors Key Learner Characteristics for Math Success The Learning Process Methodology for Math – An example: Analyzing a Function L 2 L Math Camp/Course – Recovery Course Questions and Comments

Learning is a Process Anyone’s learning process can be improved How can we help students improve their learning process? Purpose of Assessment vs. Evaluation Feedback Assessment is to improve performance Evaluation is to judge to punish or reward SII: Strengths, Areas for Improvement, Insights : trengths, Areas for mprovement,

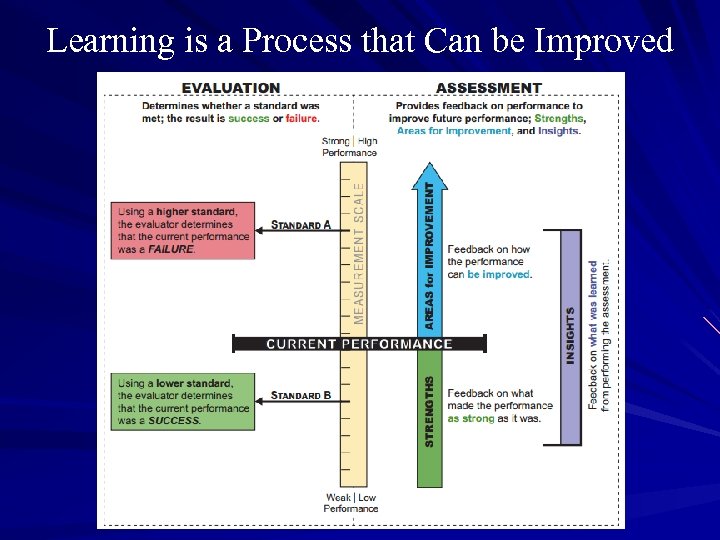Learning is a Process that Can be Improved

Major Areas of Process Education

Mathematics Classroom Culture – 14 Aspects (pages 2 -5) Challenge Cognitive Complexity Control Delivery Design Efficacy Feedback Measurement Ownership Relationship Scope of Learning Self-Awareness Social Orientation Transparentcy

Common Risk Factors for All Development Students (first page) Lacks Self-Discipline Afraid of Failure No Sense of Self. Efficacy Unmotivated Fixed Mindset Teacher Pleaser Unchallenged (bored) Memorizes Instead of Thinking Doesn’t Transfer or Generalize Knowledge Highly Judgmental Minimal Meta-cognitive Awareness Insecure Public Speaker

Risk Factors Specific to Development Math Students (first page) Placement in Courses Students’ Current Learning Process Prerequisite Knowledge Reading Mathematics Critical Thinking Skills Willingness to Struggle Problem Solving Misconceptions

Classroom Practices Assessment: SII – Strengths, Areas for Improvement, Insights Reading logs and how to use them Questions at the beginning of class Ask students to give reasons for the steps you do at the board

Steps Say your becauses.

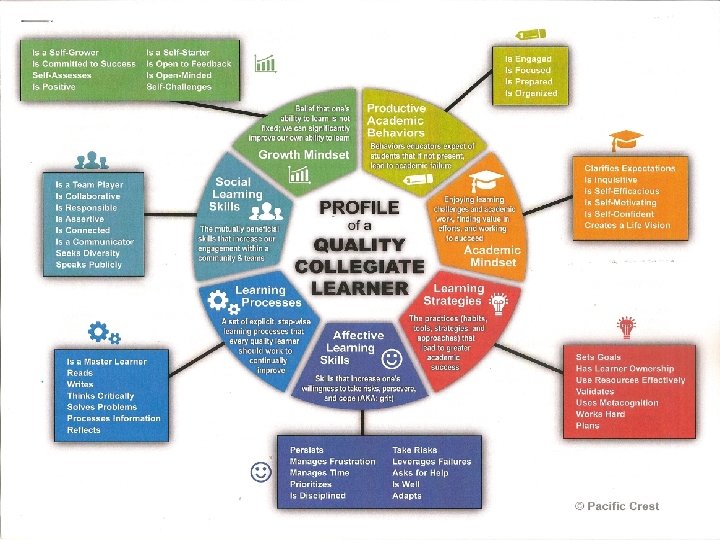
Common Key Characteristics for Academic and Math Success Thinks Critically Validates Generalizes Persists Speaks Publicly Focuses Uses Meta-cognition

Characteristics of a Profile of a Quality Mathematical Collegiate Learner (p 6) Mindset Reasoning Thinking Modeling Learning Problem Solving Communications

Mindset Are Skeptical Are Precise Enjoy Productive Struggle Are Self-reliant Reasoning Make Conjectures Seek Counter Examples Are Logical Identify Dead Ends

Thinking Abstract Visualize Use Multiple Representations Make Connects Modeling Build Models Are Tool Users Innovate Manipulate Data

Learning Interpret Notation Analyze Examples Think Analytically Transfer Knowledge Problem Solving Identify & Define Problems Identify Key Issues Identify Assumptions Reuse Solutions

Communicating Translate Teach Think on Your Feet Build Vocabulary

Learning Process Methodology

Importance of LPM Authors: design of materials Faculty: facilitation of learning Students: learning process Course assessors: measurement to improve – Learning of content – Improvement of learning skills

Learning Process Methodology (LPM) Why Orientation Prerequisites Learning Objectives Performance Criteria Vocabulary Information Plan Models/Examples Critical Thinking Q’s Applications Problem Solving Self-assessment Research

LPM 1. Why 8. Plan 2. Orientation 9. Models 3. Prerequisites 10. CTQs 4. Learning Objectives 11. Applications 5. Performance Criteria 12. Problem Solving 6. Vocabulary 7. Information 13. Self-assessment 14. Research

LPM Adapted for Mathematics (p 8) 1. Why 1. 2. Orientation 2. 3. Prerequisites 3. 4. Learning Objectives 4. 5. Performance Criteria 5. 6. 6. Vocabulary 7. Information 7. Purpose Discovery Expectations for Learning What do you already know? Required math language Information needed for learning Learning Resources (data sets, software tools, simulations, etc. )

LPM Adapted for Math (cont’d) 8. Plan 8. Classroom Activity • • • 9. Models 10. CTQs 11. Applications 12. Problem Solving Summarize and Review Steps 1 -7 Plan Models Critical Thinking Questions Performance Criteria Demonstrate Your Understanding 10. Hardest Problem – Generalize Knowledge 11. Making it Matter – Problem Solving 9. 13. Self-assessment 14. Research 12. Identify and Correct the Errors - Content 13. Learning to Learn Mathematics – Discipline 14. Assess Learning Performance – Learning Process

An Example Analyzing a Function Section 2. 5 of Quantitative Reasoning and Problem Solving Companion Website

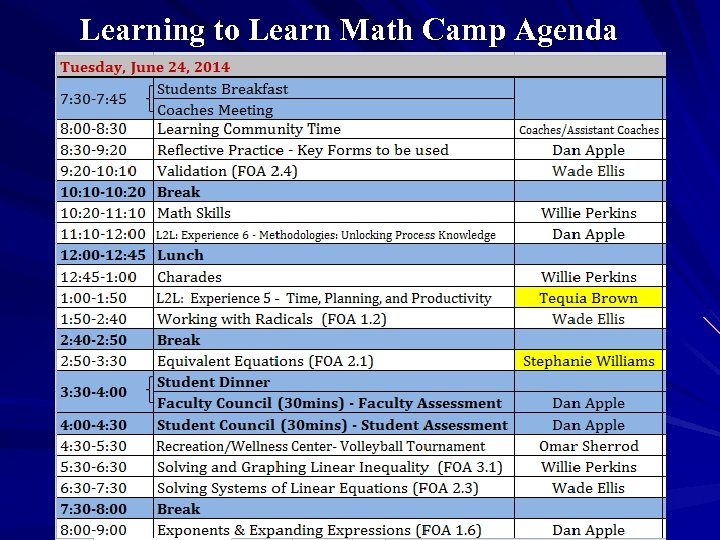Learning to Learn Math Camp Agenda

L 2 L Experiences

FOA

What are your comments and questions?

http: //www. processeducation. org/peconf/index. html

References and Links Pathfinder for 25 Years of Process Education Scholarship - http: //www. processeducation. org/ijpe/2016/pathfinder/ Risk Factors - http: //www. processeducation. org/ijpe/archive. htm – Seventh Edition (2015) Last article 8 Additional Risk Factors for Math – in handout LPM for Mathematics- in handout Academy of Process Education’s International Journal of Process Education - http: //www. processeducation. org/ijpe/archive. htm

References and Links (cont’d) PQCL diagram - http: //www. pcrest. com/PC/Reflections/issue 28/graphic 2 a. jpg Key Characteristics for Academic Success paper, including PQCL http: //www. processeducation. org/ijpe/2016_2/2016_success 2. pdf Learning to Learn Camp – http: //www. learningtolearncamp. com/ Recovery Course - http: //pcrest. com/recovery/

References and Links (cont’d) Transformation of Education Learning Object – http: //www. transformation-of-education. com/ http: //www. processeducation. org/ijpe/2011/transformationh. pdf Timeline for PE Scholarship – http: //www. processeducation. org/ijpe/25/timeline/ Learning to Learn: Becoming a Self-Grower – http: //www. pcrest. com/L 2 L_flyer 2. pdf Quantitative Reasoning and Problem Solving – http: //pcrest. com/PC/pub/2014/QRPS_course_design. pdf

Additional Slides Here a set of slides on the description of each aspect of the Transformation of Education, but not presented during the talk.

What is a Mathematics Education Culture? Challenge: The degree to which increasing the level of difficulty is used in order to grow capacity for learning and performing Cognitive Complexity: The degree to which training and doing is elevated to problem solving & research Control: The locus of power/authority for the learning situation or experience

Math Culture (cont’d) Delivery: The means by which information/knowledge is obtained by learners Design: The purposeful arrangement of instructional environment, materials, and experiences to support learning Efficacy: The well-founded belief in one's capacity to change and to make a difference Feedback: Information about what was observed in a performance or work product

Math Culture (cont’d) Measurement: The process of determining the level of quality surrounding a performance or product Ownership: The degree to which the learner accepts responsibility and accountability for achieving learning outcomes Relationship: The degree of emotional investment an instructor or mentor has in his or her students or mentees

Math Culture (cont’d) Scope of Learning: The contexts across which learning occurs and its application is demonstrated Self-awareness: The degree to which reflective and self-assessment practices are used by the individual to foster the growth of his or her earning skills across the cognitive, affective, and social domains

Math Culture (cont’d) Social Orientation: The investment, interdependence, and responsibility for learning throughout a community Transparency: The degree to which stakeholders can view individual, team or collective performance