Learning etc Spring 2007 Juris Vīksna Major

Learning etc Spring 2007, Juris Vīksna

Major Paradigms of Machine Learning n Rote Learning -- One-to-one mapping from inputs to stored representation. "Learning by memorization. ” Association-based storage and retrieval. n Clustering n Analogue -- Determine correspondence between two different representations n Induction -- Use specific examples to reach general conclusions n Discovery -- Unsupervised, specific goal not given n Genetic Algorithms n Neural Networks n Reinforcement -- Feedback (positive or negative reward) given at end of a sequence of steps. n Assign reward to steps by solving the credit assignment problem--which steps should receive credit or blame for a final result?

Feedback & Prior Knowledge n n Supervised learning: inputs and outputs available Reinforcement learning: evaluation of action Unsupervised learning: no hint of correct outcome Background knowledge is a tremendous help in learning

Supervised Concept Learning n Given a training set of positive and negative examples of a concept n n n Usually each example has a set of features/attributes Construct a description that will accurately classify whether future examples are positive or negative. That is, learn some good estimate of function f given a training set {(x 1, y 1), (x 2, y 2), . . . , (xn, yn)} where each yi is either + (positive) or - (negative). n f is a function of the features/attributes

Inductive Learning Framework n n n Raw input data from sensors are preprocessed to obtain a feature vector, X, that adequately describes all of the relevant features for classifying examples. Each x is a list of (attribute, value) pairs. For example, X = [Person: Sue, Eye. Color: Brown, Age: Young, Sex: Female] The number and names of attributes (aka features) is fixed (positive, finite). Each attribute has a fixed, finite number of possible values. Each example can be interpreted as a point in an ndimensional feature space, where n is the number of attributes.

Inductive Learning n Key idea: n n n To use specific examples to reach general conclusions Given a set of examples, the system tries to approximate the evaluation function. Also called Pure Inductive Inference

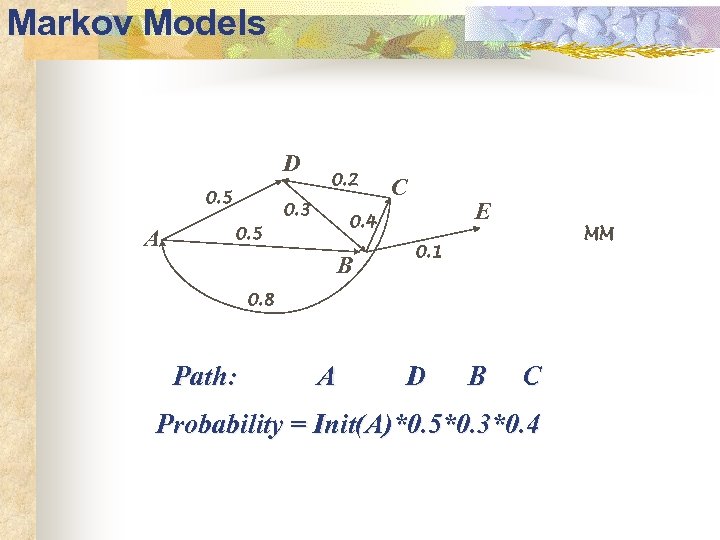Markov Models D 0. 5 A 0. 2 0. 3 C E 0. 4 0. 5 B MM 0. 1 0. 8 Path: A D B C Probability = Init(A)*0. 5*0. 3*0. 4

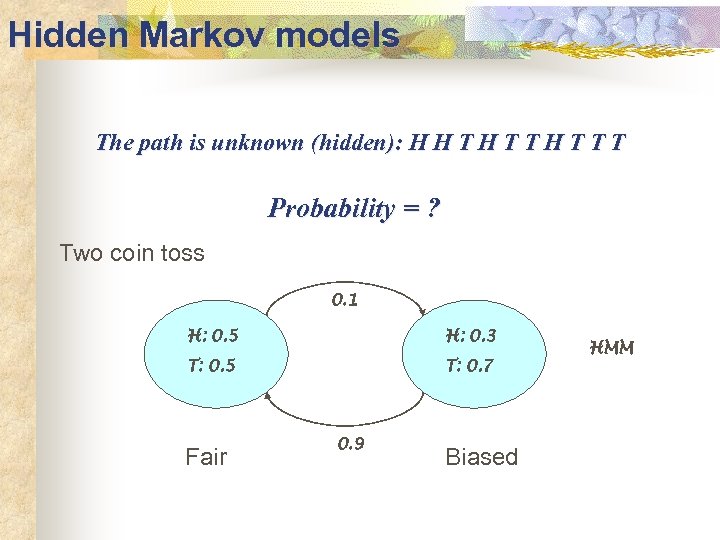Hidden Markov models The path is unknown (hidden): H H T T T Probability = ? Two coin toss 0. 1 H: 0. 5 H: 0. 3 T: 0. 5 T: 0. 7 Fair 0. 9 Biased HMM

Hidden Markov models 0. 21 0. 12 1 0. 13 0. 31 2 0. 32 0. 23 3 0. 37

HMM- Example [Adapted from R. Altman]

Three Basic Problems for HMMs [Adapted from R. Altman]

Example - Problem 2 [Adapted from R. Altman]

Problem 1 [Adapted from R. Altman]

Problem 1 [Adapted from R. Altman]

Problem 2 - Viterbi algorithm [Adapted from R. Altman]

Problem 2 - Viterbi algorithm [Adapted from R. Altman]

Problem 3? [Adapted from R. Altman]

Problem 3? [Adapted from R. Altman]

Problem 3? [Adapted from R. Altman]

Problem 3? [Adapted from R. Altman]

Inductive Learning by Nearest-Neighbor Classification n One simple approach to inductive learning is to save each training example as a point in feature space Classify a new example by giving it the same classification (+ or -) as its nearest neighbor in Feature Space. n A variation involves computing a weighted sum of class of a set of neighbors where the weights correspond to distances n Another variation uses the center of class The problem with this approach is that it doesn't necessarily generalize well if the examples are not well "clustered. "

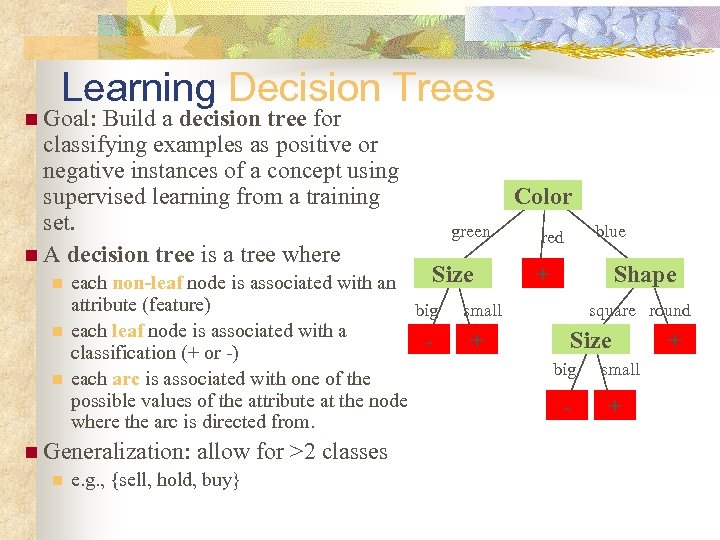Learning Decision Trees n Goal: Build a decision tree for classifying examples as positive or negative instances of a concept using supervised learning from a training set. n A decision tree is a tree where n n n green Size each non-leaf node is associated with an attribute (feature) big small each leaf node is associated with a + classification (+ or -) each arc is associated with one of the possible values of the attribute at the node where the arc is directed from. n Generalization: n Color allow for >2 classes e. g. , {sell, hold, buy} blue red + Shape square round Size big - small + +

Bias n n Bias: any preference for one hypothesis over another, beyond mere consistency with the examples. Since there almost always a large number of possible consistent hypotheses, all learning algorithms exhibit some sort of bias.

Example of Bias Is this a 7 or a 1? Some may be more biased toward 7 and others more biased toward 1.

Preference Bias: Ockham's Razor n n n Aka Occam’s Razor, Law of Economy, or Law of Parsimony Principle stated by William of Ockham (1285 -1347/49), a scholastic, that n “non sunt multiplicanda entia praeter necessitatem” n or, entities are not to be multiplied beyond necessity. The simplest explanation that is consistent with all observations is the best. Therefor, the smallest decision tree that correctly classifies all of the training examples is best. Finding the provably smallest decision tree is NP-Hard, so instead of constructing the absolute smallest tree consistent with the training examples, construct one that is pretty small.

Inductive Learning and Bias n n n Suppose that we want to learn a function f(x) = y and we are given some sample (x, y) pairs, as in figure (a). There are several hypotheses we could make about this function, e. g. : (b), (c) and (d). A preference for one over the others reveals the bias of our learning technique, e. g. : n n n prefer piece-wise functions prefer a smooth function prefer a simple function and treat outliers as noise

ID 3 n. A greedy algorithm for Decision Tree Construction developed by Ross Quinlan, 1987 n Consider a smaller tree a better tree n Top-down construction of the decision tree by recursively selecting the "best attribute" to use at the current node in the tree, based on the examples belonging to this node. n Once the attribute is selected for the current node, generate children nodes, one for each possible value of the selected attribute. n Partition the examples of this node using the possible values of this attribute, and assign these subsets of the examples to the appropriate child node. n Repeat for each child node until all examples associated with a node are either all positive or all negative.

Choosing the Best Attribute n The key problem is choosing which attribute to split a given set of examples. n Some possibilities are: n Random: Select any attribute at random n Least-Values: Choose the attribute with the smallest number of possible values (fewer branches) n Most-Values: Choose the attribute with the largest number of possible values (smaller subsets) n Max-Gain: Choose the attribute that has the largest expected information gain, i. e. select attribute that will result in the smallest expected size of the subtrees rooted at its children. n The ID 3 algorithm uses the Max-Gain method of selecting the best attribute.

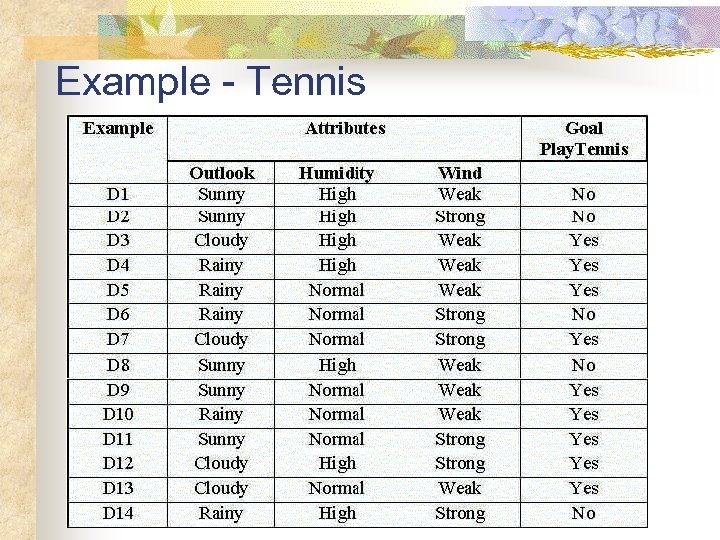Example - Tennis

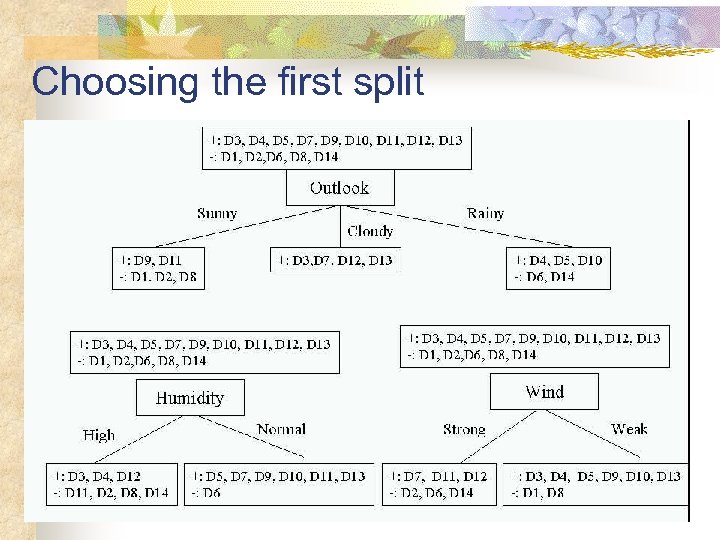Choosing the first split

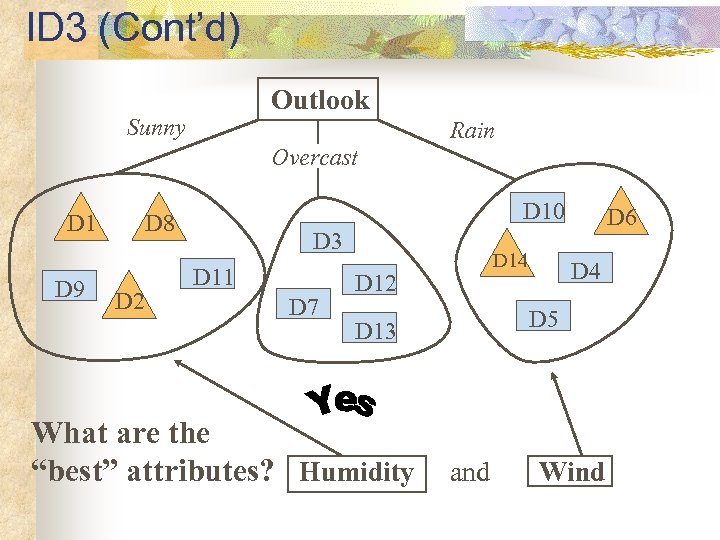ID 3 (Cont’d) Outlook Sunny Rain Overcast D 1 D 9 D 10 D 8 D 2 D 3 D 11 D 7 D 14 D 12 D 4 D 5 D 13 What are the “best” attributes? Humidity D 6 and Wind

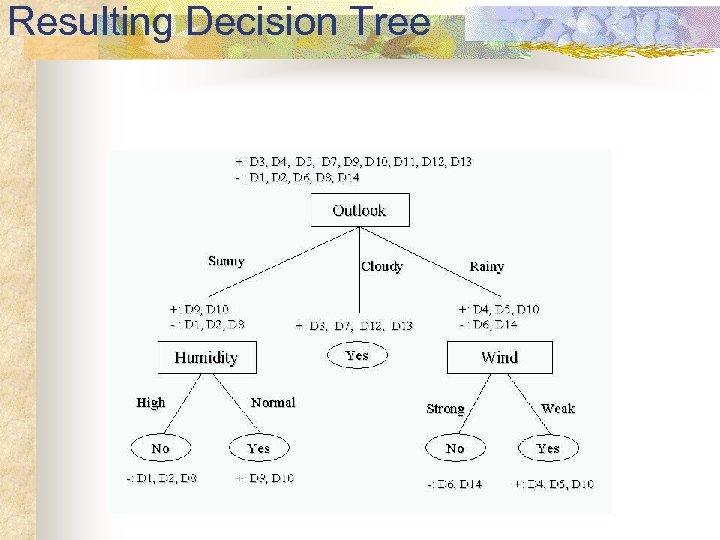Resulting Decision Tree

Information Theory Background n n n If there are n equally probable possible messages, then the probability p of each is 1/n Information conveyed by a message is -log(p) = log(n) Eg, if there are 16 messages, then log(16) = 4 and we need 4 bits to identify/send each message. In general, if we are given a probability distribution P = (p 1, p 2, . . , pn) the information conveyed by distribution (aka Entropy of P) is: I(P) = -(p 1*log(p 1) + p 2*log(p 2) +. . + pn*log(pn))

Information Theory Background n If a set T of records is partitioned into disjoint exhaustive classes (C 1, C 2, . . , Ck) on the basis of the value of the categorical attribute, then the information needed to identify the class of an element of T is Info(T) = I(P) where P is probability distribution of partition (C 1, C 2, . . , Ck): P = (|C 1|/|T|, |C 2|/|T|, . . . , |Ck|/|T|) n If we partition T w. r. t attribute X into sets {T 1, T 2, . . , Tn} then the information needed to identify the class of an element of T becomes the weighted average of the information needed to identify the class of an element of Ti, i. e. the weighted average of Info(Ti): Info(X, T) = |Ti|/|T| * Info(Ti) = |Ti|/|T| * log |Ti|/|T|

Gain n Consider the quantity Gain(X, T) defined as Gain(X, T) = Info(T) - Info(X, T) n This represents the difference between n n information needed to identify an element of T and information needed to identify an element of T after the value of attribute X has been obtained, that is, this is the gain in information due to attribute X. n We can use this to rank attributes and to build decision trees where at each node is located the attribute with greatest gain among the attributes not yet considered in the path from the root. n The intent of this ordering are twofold: n n To create small decision trees so that records can be identified after only a few questions. To match a hoped for minimality of the process represented by the records being considered (Occam's Razor).

Information Theory Background n n n The entropy is the average number of bits/message needed to represent a stream of messages. Examples: n if P is (0. 5, 0. 5) then I(P) is 1 n if P is (0. 67, 0. 33) then I(P) is 0. 92, n if P is (1, 0) then I(P) is 0. The more uniform is the probability distribution, the greater is its information gain/entropy.

Information Theory Background

Information Theory Background

Information Theory Background

Information Theory Background

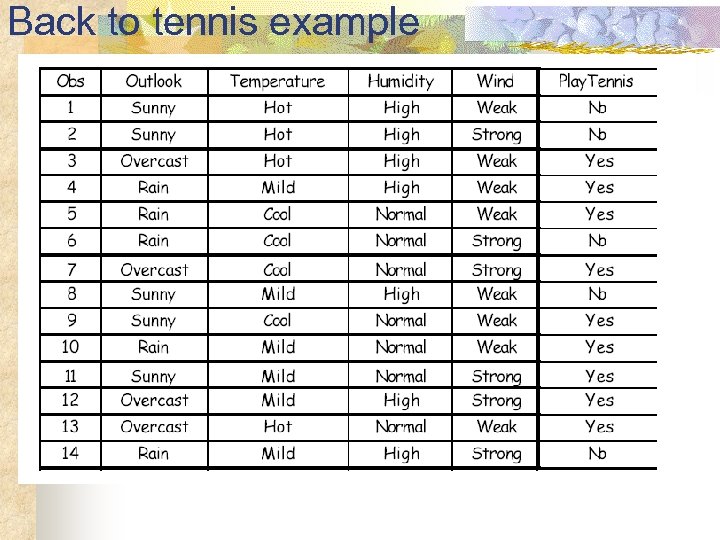Back to tennis example

Back to tennis example

Back to tennis example

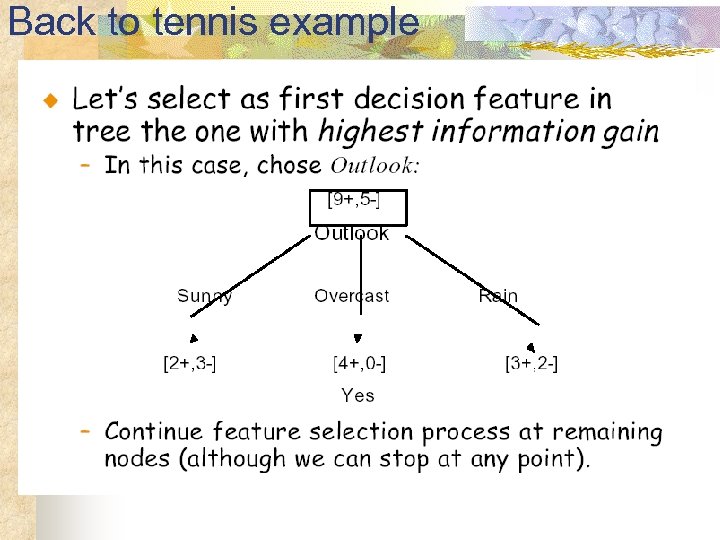Back to tennis example

Example: Huffman code n n In 1952 MIT student David Huffman devised, in the course of doing a homework assignment, an elegant coding scheme which is optimal in the case where all symbols probabilities are integral powers of 1/2. A Huffman code can be built in the following manner: n Rank all symbols in order of probability of occurrence. n Successively combine the two symbols of the lowest probability to form a new composite symbol; eventually we will build a binary tree where each node is the probability of all nodes beneath it. n Trace a path to each leaf, noticing the direction at each node.

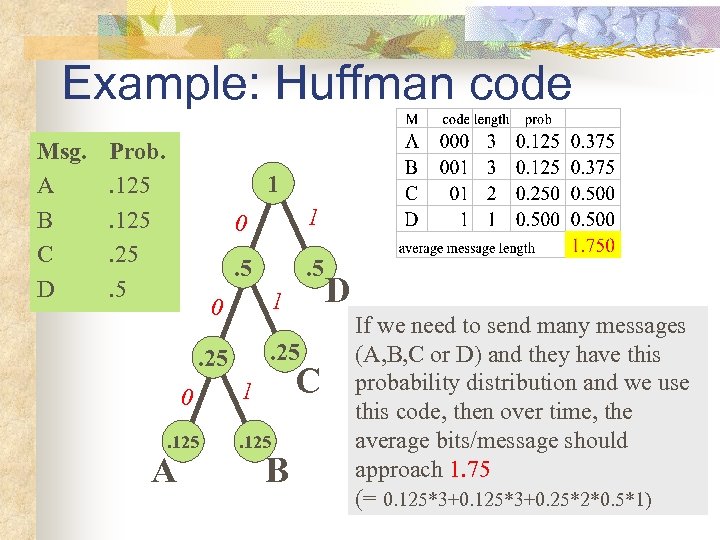Example: Huffman code Msg. A B C D Prob. . 125. 25. 5 1 0 1 . 5 1 0 . 25 0. 125 A C 1. 125 B D If we need to send many messages (A, B, C or D) and they have this probability distribution and we use this code, then over time, the average bits/message should approach 1. 75 (= 0. 125*3+0. 25*2*0. 5*1)

ID 3 algorithm is used to build a decision tree, given a set of non-categorical The ID 3 attributes C 1, C 2, . . , Cn, the categorical attribute C, and a training set T of records. function ID 3 (R: a set of non-categorical attributes, C: the categorical attribute, S: a training set) returns a decision tree; begin If S is empty, return a single node with value Failure; If every example in S has the same value for categorical attribute, return single node with that value; If R is empty, then return a single node with most frequent of the values of the categorical attribute found in examples S; [note: there will be errors, i. e. , improperly classified records]; Let D be attribute with largest Gain(D, S) among R’s attributes; Let {dj| j=1, 2, . . , m} be the values of attribute D; Let {Sj| j=1, 2, . . , m} be the subsets of S consisting respectively of records with value dj for attribute D; Return a tree with root labeled D and arcs labeled d 1, d 2, . . , dm going respectively to the trees ID 3(R-{D}, C, S 1), ID 3(R-{D}, C, S 2) , . . , ID 3(R-{D}, C, Sm); end ID 3;

Expressiveness of Decision Trees n n Any Boolean function can be written as a decision tree Limitations n n Can only describe one object at a time. Some functions require an exponentially large decision tree. n n n E. g. Parity function, majority function Decision trees are good for some kinds of functions, and bad for others. There is no one efficient representation for all kinds of functions.

How well does it work? Many case studies have shown that decision trees are at least as accurate as human experts. n A study for diagnosing breast cancer had humans correctly classifying the examples 65% of the time, and the decision tree classified 72% correct. n British Petroleum designed a decision tree for gasoil separation for offshore oil platforms that replaced an earlier rule-based expert system. n Cessna designed an airplane flight controller using 90, 000 examples and 20 attributes per example.

Extensions of the Decision Tree Learning Algorithm n n n n Using gain ratios Real-valued data Noisy data and Overfitting Generation of rules Setting Parameters Cross-Validation for Experimental Validation of Performance C 4. 5 (and C 5. 0) is an extension of ID 3 that accounts for unavailable values, continuous attribute value ranges, pruning of decision trees, rule derivation, and so on. Incremental learning

Using Gain Ratios n The notion of Gain introduced earlier favors attributes that have a large number of values. n If we have an attribute D that has a distinct value for each record, then Info(D, T) is 0, thus Gain(D, T) is maximal. n To compensate for this Quinlan suggests using the following ratio instead of Gain: Gain. Ratio(D, T) = Gain(D, T) / Split. Info(D, T) n Split. Info(D, T) is the information due to the split of T on the basis of value of categorical attribute D. Split. Info(D, T) = I(|T 1|/|T|, |T 2|/|T|, . . , |Tm|/|T|) where {T 1, T 2, . . Tm} is the partition of T induced by value of D.

Real-valued data n n n Select a set of thresholds defining intervals; each interval becomes a discrete value of the attribute We can use some simple heuristics n n We can use domain knowledge n n always divide into quartiles divide age into infant (0 -2), toddler (3 - 5), and school aged (5 -8) or treat this as another learning problem n try a range of ways to discretize the continuous variable and see which yield “better results” w. r. t. some metric.

Noisy data and Overfitting n Many n n n Two examples have same attribute/value pairs, but different classifications Some values of attributes are incorrect because of errors in the data acquisition process or the preprocessing phase The classification is wrong (e. g. , + instead of -) because of some error n Some n n kinds of "noise" that could occur in the examples: attributes are irrelevant to the decision-making process, e. g. , color of a die is irrelevant to its outcome. Irrelevant attributes can result in overfitting the training data. n Overfitting: n n n learning result fits data (training examples) well but does not hold for unseen data (poor generalization) Often need to compromise fitness to data and generalization power Overfitting is a problem common to all methods that learn from data

Noisy data and Overfitting (b and (c): better fit for data, poor generalization (d): not fit for the outlier (possibly due to noise), but better generalization n Fix n n overfitting/overlearning problem By cross validation (see later) By pruning lower nodes in the decision tree. For example, if Gain of the best attribute at a node is below a threshold, stop and make this node a leaf rather than generating children nodes.

Pruning Decision Trees n Pruning of the decision tree is done by replacing a whole subtree by a leaf node. n The replacement takes place if a decision rule establishes that the expected error rate in the subtree is greater than in the single leaf. E. g. , n n n Training: eg, one training red success and one training blue Failures Test: three red failures and one blue success Consider replacing this subtree by a single Failure node. n After replacement we will have only two errors instead of five failures. Color red 1 success 0 failure blue 0 success 1 failure Color red 1 success 3 failure blue 1 success 1 failure FAILURE 2 success 4 failure

Incremental Learning n. Incremental learning n Change can be made with each training example n Non-incremental learning is also called batch learning n Good for n adaptive n when n Often system (learning while experiencing) environment undergoes changes with n Higher computational cost n Lower quality of learning results n ITI (by U. Mass): incremental DT learning package

Evaluation Methodology n Standard methodology: cross validation 1. Collect a large set of examples (all with correct classifications!). 2. Randomly divide collection into two disjoint sets: training and test. 3. Apply learning algorithm to training set giving hypothesis H 4. Measure performance of H w. r. t. test set n Important: keep the training and test sets disjoint! n Learning is not to minimize training error (wrt data) but the error for test/cross-validation: a way to fix overfitting n To study the efficiency and robustness of an algorithm, repeat steps 2 -4 for different training sets and sizes of training sets. n If you improve your algorithm, start again with step 1 to avoid evolving the algorithm to work well on just this collection.

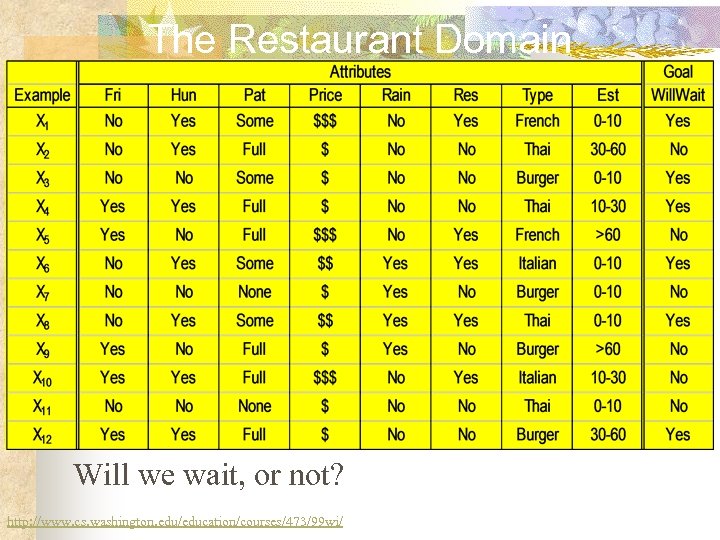The Restaurant Domain Will we wait, or not? http: //www. cs. washington. edu/education/courses/473/99 wi/

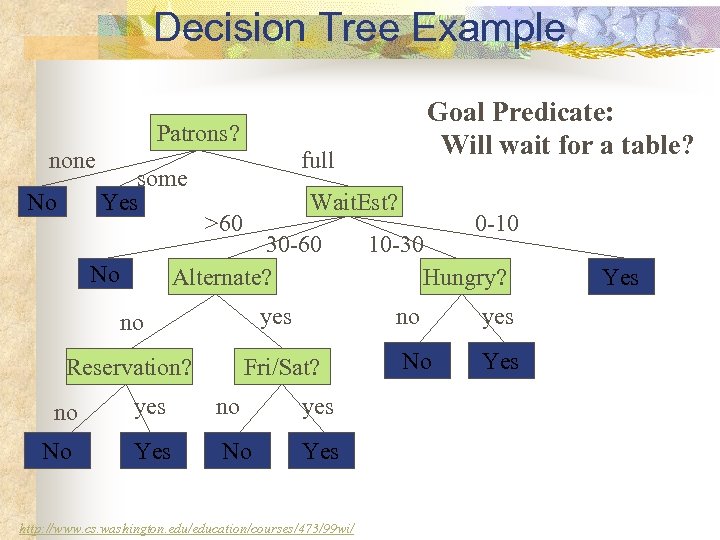Decision Tree Example Goal Predicate: Will wait for a table? Patrons? none No some Yes full Wait. Est? >60 30 -60 Alternate? No no yes Reservation? Fri/Sat? 0 -10 10 -30 Hungry? no no yes No Yes http: //www. cs. washington. edu/education/courses/473/99 wi/ yes No Yes

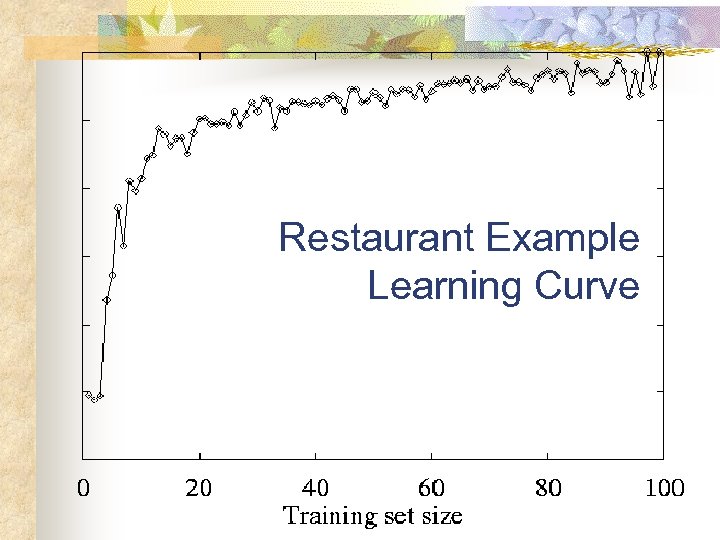Restaurant Example Learning Curve

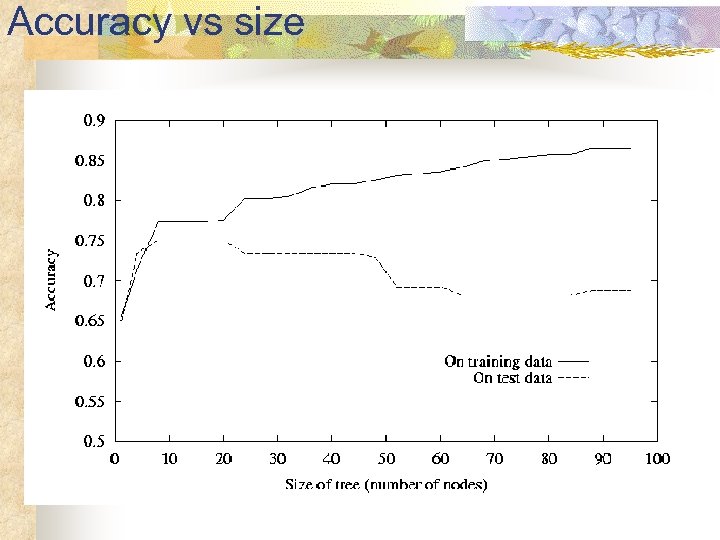Accuracy vs size

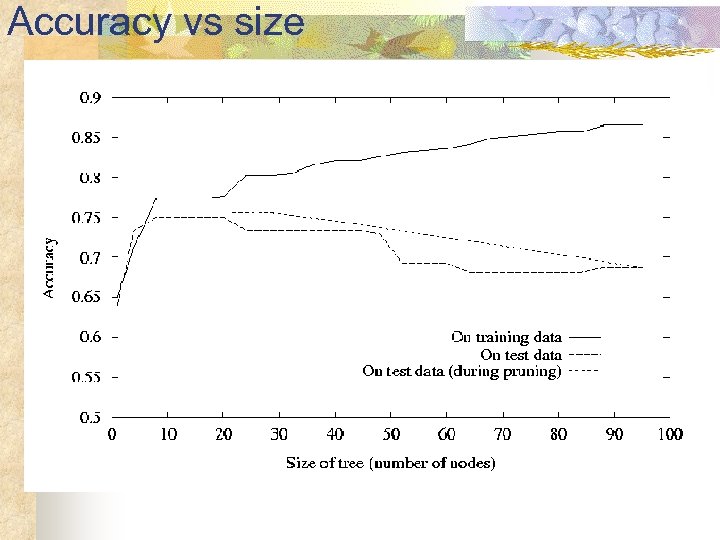Accuracy vs size

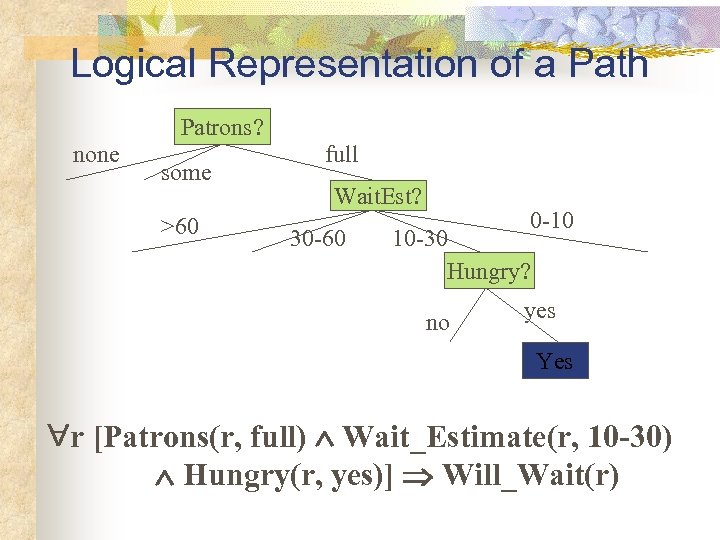Logical Representation of a Path Patrons? none some >60 full Wait. Est? 30 -60 0 -10 10 -30 Hungry? no yes Yes r [Patrons(r, full) Wait_Estimate(r, 10 -30) Hungry(r, yes)] Will_Wait(r)

Decision Trees to Rules n n n It is easy to derive a rule set from a decision tree: write a rule for each path in the decision tree from the root to a leaf. In that rule the left-hand side is easily built from the label of the nodes and the labels of the arcs. The resulting rules set can be simplified: n n Let LHS be the left hand side of a rule. Let LHS' be obtained from LHS by eliminating some conditions. We can certainly replace LHS by LHS' in this rule if the subsets of the training set that satisfy respectively LHS and LHS' are equal. A rule may be eliminated by using metaconditions such as "if no other rule applies".

C 4. 5 n C 4. 5 is an extension of ID 3 that accounts for unavailable values, continuous attribute value ranges, pruning of decision trees, rule derivation, and so on. C 4. 5: Programs for Machine Learning J. Ross Quinlan, The Morgan Kaufmann Series in Machine Learning, Pat Langley, Series Editor. 1993. 302 pages. paperback book & 3. 5" Sun disk. $77. 95. ISBN 1 -55860 -240 -2

Summary of DT Learning n n n Inducing decision trees is one of the most widely used learning methods in practice Can out-perform human experts in many problems Strengths include n n n Fast simple to implement can convert result to a set of easily interpretable rules empirically valid in many commercial products handles noisy data Weaknesses include: n n n "Univariate" splits/partitioning using only one attribute at a time so limits types of possible trees large decision trees may be hard to understand requires fixed-length feature vectors

Genetic Algorithm / Evolutionary Strategy n inspired by theory of biological evolution n n Evolutionary process for optimization n n Search proceeds through maintenance of a population of solutions Reproduction biased in favor of better individuals Diversity obtained by mutation and recombination J. Holland, Adaptation in Natural and Artificial Systems, U of Michigan Press, 1975 improves initial solutions Stochastic Search n n high probability of locating global optimal solution Local minima escape minimum value [Adapted from H. Kim]

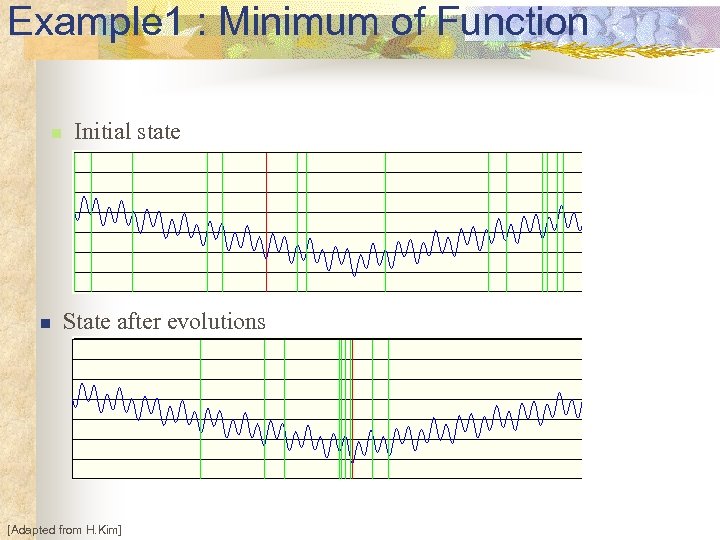Example 1 : Minimum of Function n n Initial state State after evolutions [Adapted from H. Kim]

Applications of GA n Difficult Problems such as NP-class n n n n n [Adapted from H. Kim] Nonlinear dynamical systems - predicting, data analysis Designing neural networks, both architecture and weights Robot Trajectory Planning Evolving LISP programs (genetic programming) Strategy planning Finding shape of protein molecules TSP and sequence scheduling Functions for creating images VLSI layout planning …

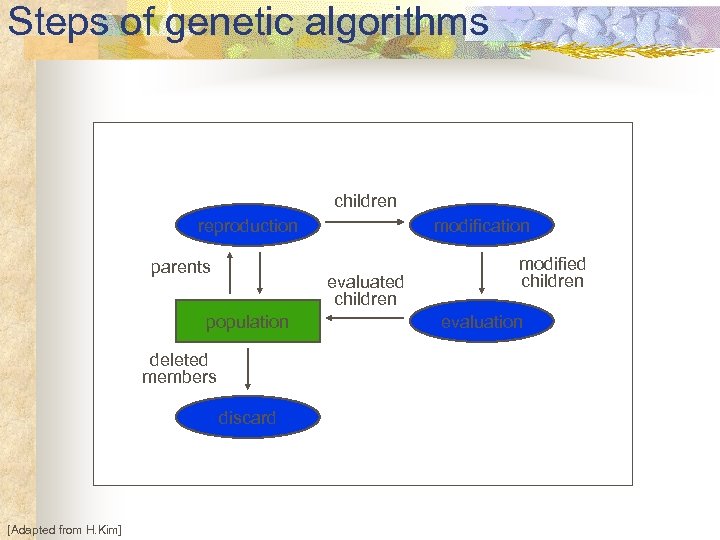Steps of genetic algorithms children reproduction parents evaluated children population deleted members discard [Adapted from H. Kim] modification modified children evaluation

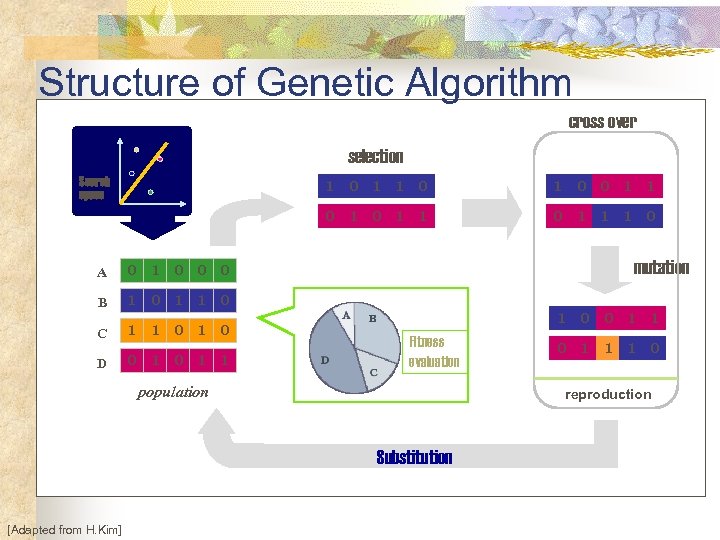Structure of Genetic Algorithm cross over selection Search space 1 0 0 1 1 C 1 0 D 0 1 1 0 0 1 1 1 0 mutation 0 1 1 0 B 1 0 A 0 1 Fitness evaluation population 0 1 1 1 0 reproduction Substitution [Adapted from H. Kim] 0

GA’s Five Decision Points n Encoding technique (“chromosome structure”) n n Evaluation function (“environment”) n n n Fitness function Selection procedure (“creation”) Generating Chromosome diversity (“evolution”) n n Mechanism to encode solution Crossover, mutation Parameter settings (practice and art) n n Termination condition (Random) Initialization of population [Adapted from H. Kim]

Encoding n n chromosome contains information about solution Several encoding schemes n n n n Binary coding K-nary coding Gray coding Real-number coding Locus-based representation vs Order-based representation Single dimensional vs multidimensional representation The most used way of encoding is a binary string Selection of encoding mechanism is based on the problem characteristics [Adapted from H. Kim]

Gray coding n n n A kind of binary coding Adjacent number differ only one bit Similar solution situated near in problem space Binary coding 0000 0001 0010 0011 0100 [Adapted from H. Kim] Gray coding 0000 0001 0010 0110

Locus-based vs Order-based n TSP problem n path representation n n Direct Order representation n [1, 4, 8, 3, 2, 7, 5, 6] = (1, 3, 6, 2, 1, 3, 1, 1) Corner representation n n [14, 48, 38, 23, 27, 56, 16] Nth in remain city list n n Location i contains index of city to visit after city i (4, 7, 2, 8, 6, 1, 5, 3) Undirected Edge Representation n n ind element is the city visited ind [1, 4, 8, 3, 2, 7, 5, 6] [4, 8, 3, 2, 7, 5, 6, 1], [8, 3, 2, 7, 5, 6, 1, 4] … are all same [148, 483, 832, 327, 275, …. ] The representation want to be valid after crossover n Partially matched crossover [Adapted from H. Kim]

Single vs multidimensional representation n n Multidimensional representation may preserve valuable information (eg. neighbor relationship) proper crossover operator required [Adapted from H. Kim]

Fitness Function n A measure of how successful an individual is in the environment n n Given chromosome, the fitness function returns a number n n Problem dependent f: S R Smooth and regular n n [Adapted from H. Kim] Similar chromosomes produce close fitness values Not have too many local extremes and isolated global extreme

Selection Operation n n Chromosomes are selected from population to be parents for crossover fitter solution has more chance of being selected n n Selection Pressure n n Models fitter offspring Difference of the probabilities of being selected between best and worst chromosomes High selection pressure – premature convergence Low selection pressure – slow converge Various Selection Schemes n Roulette Wheel Selection, Ranking Scheme, Tournament Selection, … [Adapted from H. Kim]

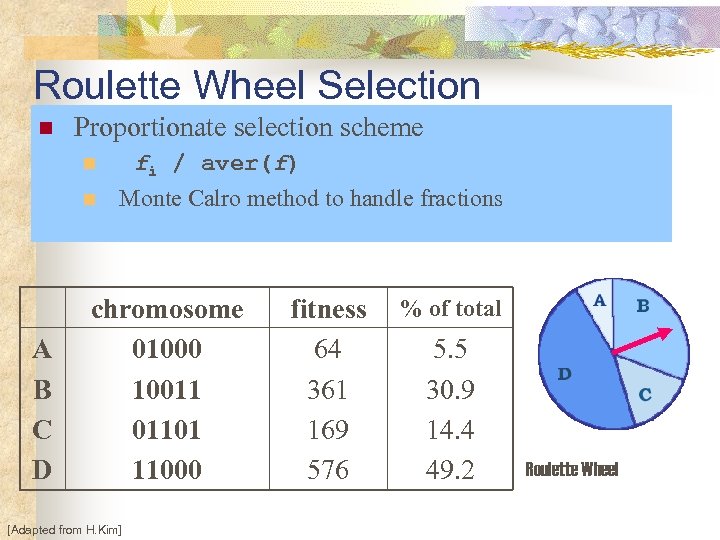Roulette Wheel Selection n Proportionate selection scheme fi / aver(f) n n A B C D Monte Calro method to handle fractions chromosome 01000 10011 01101 11000 [Adapted from H. Kim] fitness 64 361 169 576 % of total 5. 5 30. 9 14. 4 49. 2 Roulette Wheel

Rank Selection n Rank the population first, then chromosome receives fitness value determined by the ranking. n Remedy the problems of Roulette Wheel Selection n Large fitness value dominate too much All the chromosomes have a chance to be selected Slow convergence [Adapted from H. Kim]

Tournament Selection n Select two chromosome, then select better one with probability t, otherwise select worse one. High t means high selection pressure You may extend this idea a tournament to compare 2 chromosomes and select the best n n High r means high selection pressure Less computation [Adapted from H. Kim] r

Selection by Elitism n n When creating a new population, a big chance of loosing the best chromosome Keep copies of the best chromosome (or few best chromosomes) to the new population. n n The rest of the population is constructed as normal Elitism can rapidly increase the performance of GA, because it prevents a loss of the best found solution. [Adapted from H. Kim]

Generate Chromosome Diversity n n n Crossover and Mutation is the basic operation to generate diversity in solutions Crossover and Mutation schemes depends on encoding scheme Triggered stochastically (1) crossover causes recombination n important feature of GA accelerate search in early stage of evolution lead to effective combination of schemata (subsolutions) (2) mutation causes a local modification (0 1 1 0) (0 1 0 0 1 1 0) [Adapted from H. Kim] (2. 67 -49. 3 128. 68 33. 1) (2. 67 -47. 6 128. 69 33. 1)

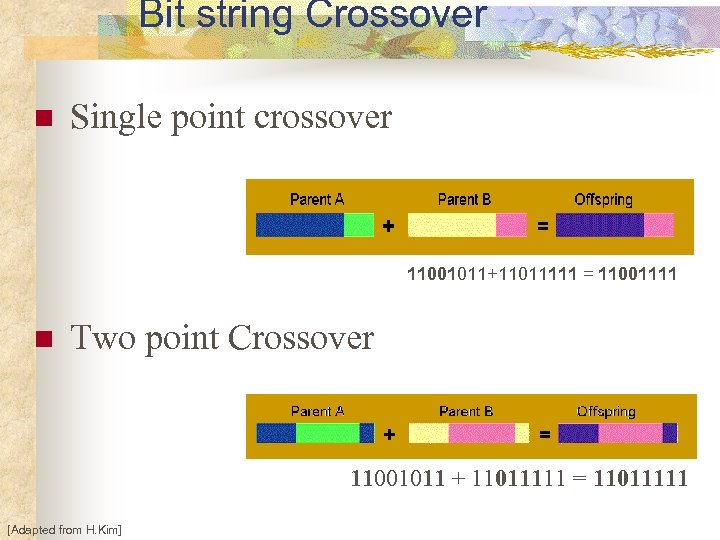Bit string Crossover n Single point crossover 11001011+11011111 = 11001111 n Two point Crossover 11001011 + 11011111 = 11011111 [Adapted from H. Kim]

Bit string Crossover n Uniform crossover : bits are randomly copied from the parents 11001011 + 1101 = 11011111 n Arithmetic crossover - arithmetic operation to make offspring 11001011 + 11011111 = 11001001 (AND) if random-number > Crossover-rate then Crossover otherwise remain unaltered [Adapted from H. Kim]

Mutation n n n (independently) Flipping bits randomly In order to get diversity controlled by Mutation rate, Pm if no mutation, only space governed by initial population is searched If Pm is too large, it becomes a random search Dynamic change of Pm depending on time n n ‘scheduling’ idea of simulated annealing Adaptive mutation n depending on distance of crossover result n [Adapted from H. Kim] near more mutation

Operational Parameters n Discrete generation model n n Continuous generation model n n a few members can be replaced at a time asynchronous operation one-at-the-time model Typical parameter values n n entire population can be replaced at a time population size : 30 -200 crossover rate : 0. 5 -1 mutation rate : 0. 001 - 0. 05 Termination condition n n [Adapted from H. Kim] Number of generations Improvement is small

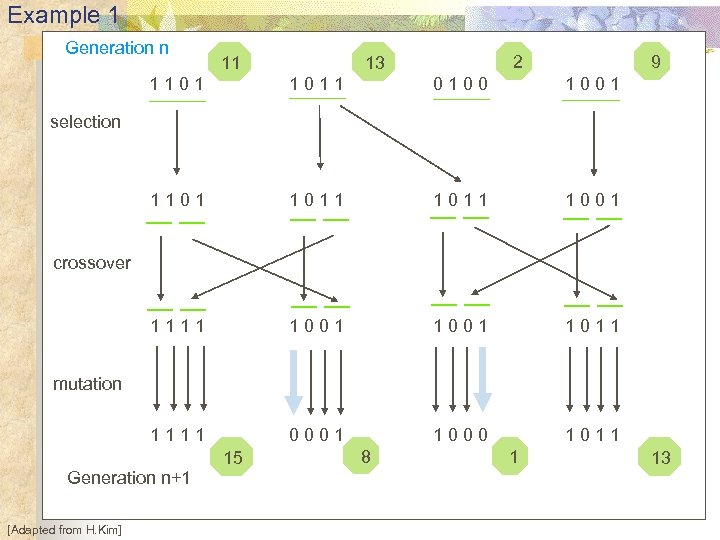Example 1 Generation n 11 2 13 9 1101 1011 0100 1001 1101 1011 1001 1111 1001 1011 1111 0001 1000 1011 selection crossover mutation Generation n+1 [Adapted from H. Kim] 15 8 1 13

Example 2 Fitness function f(x) = x 2 where 0 x 31 – decoding 5 -bit unsigned binary integer ex) 13 = 01101 – initial population (at random) population size = 4 tossing a fair coin 20 times [Adapted from H. Kim]

Example 2 Population 1 2 3 4 sum average max 01101 11000 01000 10011 01101 11000 10011 x 2 x value f(x) value fi / f expected Pselecti count 13 24 8 19 169 576 64 361 0. 14 0. 49 0. 06 0. 31 0. 58 1. 97 0. 22 1. 23 1 2 0 1 1. 00 0. 25 0. 49 mate 2 1 4 2 1170 293 576 crossover 4 4 2 2 4. 00 1. 97 x 12 25 27 16 f(x) 144 625 729 256 011001 11011 10000 sum 1754 average 439 max 729 [Adapted from H. Kim]

TSP Examples n n n Population of 16 chromosomes permutation encoding Crossover n n Single point, two point, none Mutation 1. 2. 3. 4. 5. 6. Normal Random, only improving Systematic, only improving Random improving : 1+2 Systematic improving : 1+3 no mutation [Adapted from H. Kim]

Advantages and Disadvantages of Genetic Algorithm n Parallelism (A) n n Easy to implement. (A) n n n using more individuals so that they are less likely to get stuck in a local extreme write a new chromosome and fitness function to solve a new problem Choosing and implementation of encoding and fitness function can be difficult (D) Computational time, Slower than others (D) [Adapted from H. Kim]

Genetic Algorithms [Adapted from D. Goldberg]

Genetic Algorithms [Adapted from D. Goldberg]

Genetic Algorithms [Adapted from N. Nilsson]

Genetic Algorithms [Adapted from N. Nilsson]

Genetic Algorithms [Adapted from N. Nilsson]

Genetic Algorithms [Adapted from N. Nilsson]

Genetic Algorithms [Adapted from N. Nilsson]