Learning Department of Computer Science Engineering Indian

Learning Department of Computer Science & Engineering Indian Institute of Technology Kharagpur CSE, IIT Kharagpur

Paradigms of learning • Supervised Learning – A situation in which both inputs and outputs are given – Often the outputs are provided by a friendly teacher. • Reinforcement Learning – The agent receives some evaluation of its action (such as a fine for stealing bananas), but is not told the correct action (such as how to buy bananas). • Unsupervised Learning – The agent can learn relationships among its percepts, and the trend with time CSE, IIT Kharagpur 2

Decision Trees • A decision tree takes as input an object or situation described by a set of properties, and outputs a yes/no “decision”. Decision: Whether to wait for a table at a restaurant. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. Alternate: whethere is a suitable alternative restaurant Lounge: whether the restaurant has a lounge for waiting customers Fri/Sat: true on Fridays and Saturdays Hungry: whether we are hungry Patrons: how many people are in it (None, Some, Full) Price: the restaurant’ price range (★, ★★★) Raining: whether it is raining outside Reservation: whether we made a reservation Type: the kind of restaurant (Indian, Chinese, Thai, Fastfood) Wait. Estimate: 0 -10 mins, 10 -30, 30 -60, >60. CSE, IIT Kharagpur 3

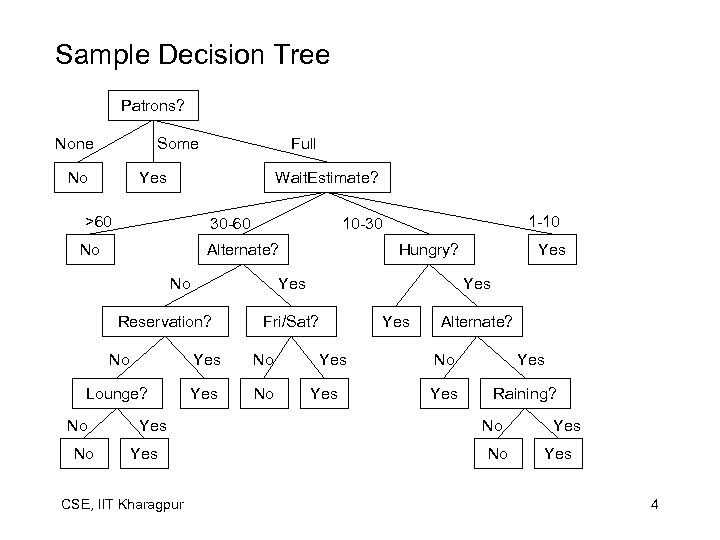Sample Decision Tree Patrons? None Some No Full Yes Wait. Estimate? >60 30 -60 No Alternate? No Yes No Lounge? Yes No No Yes CSE, IIT Kharagpur Yes Fri/Sat? No Yes Hungry? Yes Reservation? No 1 -10 10 -30 Yes Yes Alternate? No Yes Raining? No No Yes 4

Decision Tree Learning Algorithm Function Decision-Tree-Learning( examples, attributes, default ) if examples is empty then return default else if all examples have the same classification then return the classification else if attributes is empty then return Majority-Value( examples ) else best Choose-Attribute( attributes, examples ) tree a new decision tree with root test best for each value vi of best do examplesi { elements of examples with best = vi } subtree Decision-Tree-Learning( examplesi, attributes – best, Majority-Value( examples )) add a branch to tree with label vi and subtree end return tree CSE, IIT Kharagpur 5

Neural Networks • A neural network consists of a set of nodes (neurons/units) connected by links – Each link has a numeric weight associated with it • Each unit has: – – a set of input links from other units, a set of output links to other units, a current activation level, and an activation function to compute the activation level in the next time step. CSE, IIT Kharagpur 6

Basic definitions aj Wj, i Input Links ai = g( ini ) ini g S Input Activation Function ai Output Links Output • The total weighted input is the sum of the input activations times their respective weights: • In each step, we compute: CSE, IIT Kharagpur 7

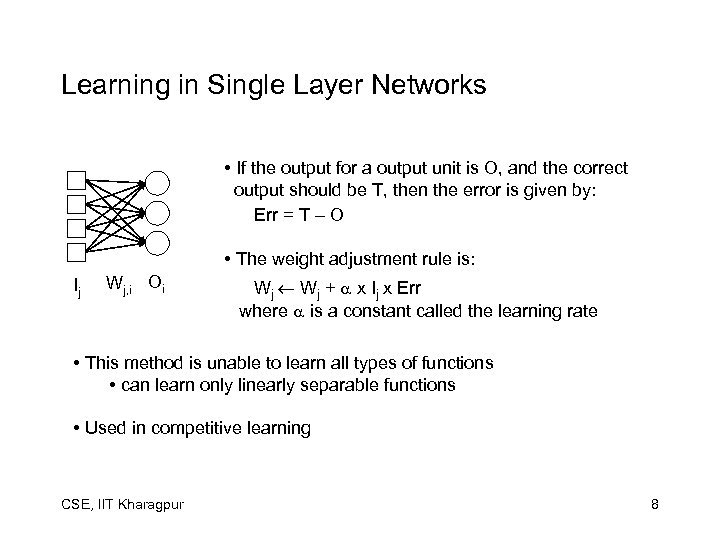Learning in Single Layer Networks • If the output for a output unit is O, and the correct output should be T, then the error is given by: Err = T – O • The weight adjustment rule is: Ij Wj, i Oi Wj + x Ij x Err where is a constant called the learning rate • This method is unable to learn all types of functions • can learn only linearly separable functions • Used in competitive learning CSE, IIT Kharagpur 8

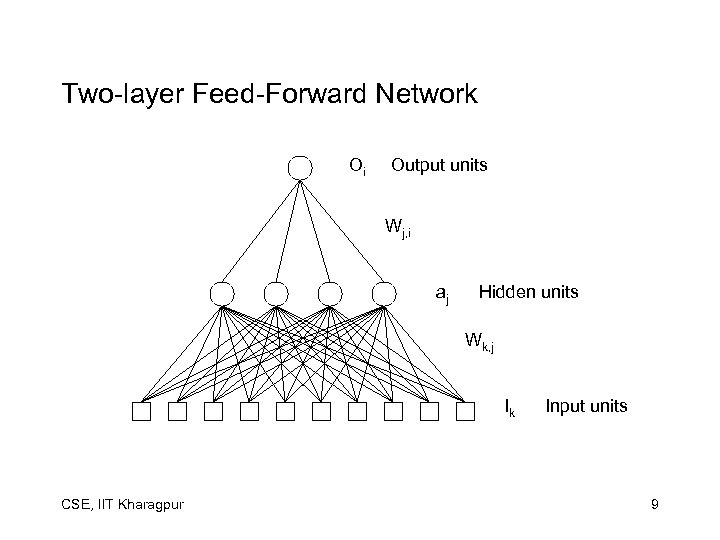Two-layer Feed-Forward Network Oi Output units Wj, i aj Hidden units Wk, j Ik CSE, IIT Kharagpur Input units 9

Back-Propagation Learning • Erri = (Ti – Oi) is the error at the output node • The weight update rule for the link from unit j to output unit i is: Wj, i + x aj x Erri x g'(ini) where g' is the derivative of the activation function g. • Let i = Erri g'(ini). Then we have: Wj, i + x aj x i CSE, IIT Kharagpur 10

Error Back-Propagation • For updating the connections between the inputs and the hidden units, we need to define a quantity analogous to the error term for the output nodes – Hidden node j is responsible for some fraction of the error i each of the output nodes to which it connects – So, the i values are divided according to the strength of the connection between the hidden node and the output node, and propagated back to provide the j values for the hidden layer • The weight update rule for weights between the inputs and the hidden layer is: Wk, j + x Ik x j CSE, IIT Kharagpur 11

The theory • The total error is given by: • Only one of the terms in the summation over i and j depends on a particular Wj, i, so all other terms are treated as constants with respect to Wj, i • Similarly: CSE, IIT Kharagpur 12