f3923e4ea1e6c63a03fc0de37b3951ac.ppt
- Количество слайдов: 58
 Learning Data Representations with “Partial. Supervision ” Ariadna Quattoni
Learning Data Representations with “Partial. Supervision ” Ariadna Quattoni
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
 Semi-Supervised Learning “Raw” Feature Space Output Space Core Task: Learn a function from X to Y Labeled Dataset (Small) Classical Setting Unlabeled Dataset (Large) Partial Supervision Setting Partially Labeled Dataset (Large)
Semi-Supervised Learning “Raw” Feature Space Output Space Core Task: Learn a function from X to Y Labeled Dataset (Small) Classical Setting Unlabeled Dataset (Large) Partial Supervision Setting Partially Labeled Dataset (Large)
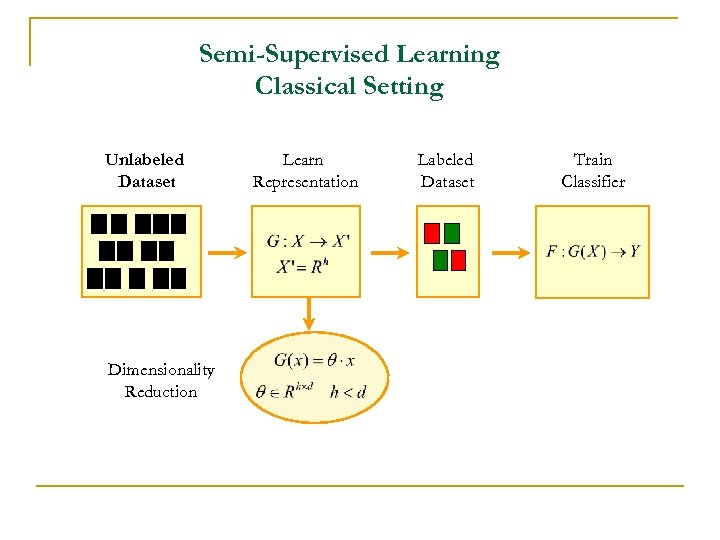 Semi-Supervised Learning Classical Setting Unlabeled Dataset Dimensionality Reduction Learn Representation Labeled Dataset Train Classifier
Semi-Supervised Learning Classical Setting Unlabeled Dataset Dimensionality Reduction Learn Representation Labeled Dataset Train Classifier
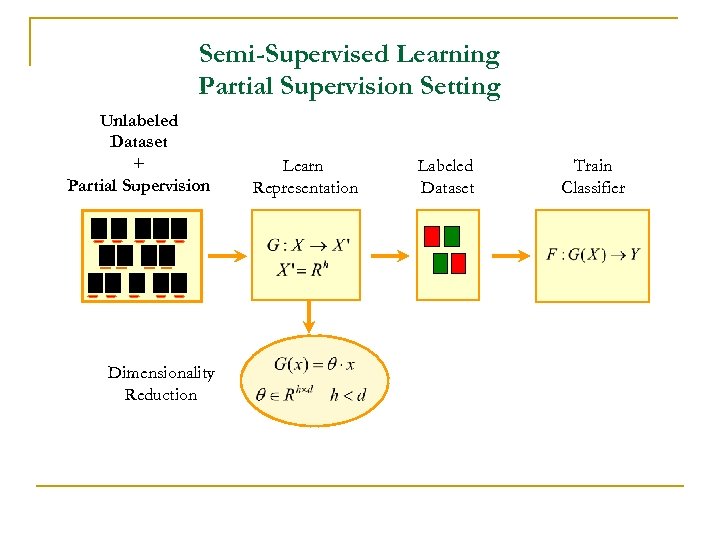 Semi-Supervised Learning Partial Supervision Setting Unlabeled Dataset + Partial Supervision Dimensionality Reduction Learn Representation Labeled Dataset Train Classifier
Semi-Supervised Learning Partial Supervision Setting Unlabeled Dataset + Partial Supervision Dimensionality Reduction Learn Representation Labeled Dataset Train Classifier
 Why is “learning representations” useful? q Infer the intrinsic dimensionality of the data. q Learn the “relevant” dimensions. q Infer the hidden structure.
Why is “learning representations” useful? q Infer the intrinsic dimensionality of the data. q Learn the “relevant” dimensions. q Infer the hidden structure.
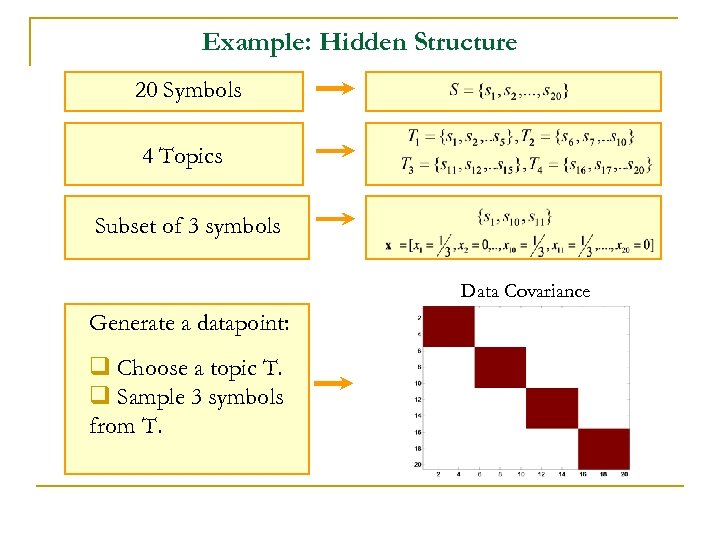 Example: Hidden Structure 20 Symbols 4 Topics Subset of 3 symbols Data Covariance Generate a datapoint: q Choose a topic T. q Sample 3 symbols from T.
Example: Hidden Structure 20 Symbols 4 Topics Subset of 3 symbols Data Covariance Generate a datapoint: q Choose a topic T. q Sample 3 symbols from T.
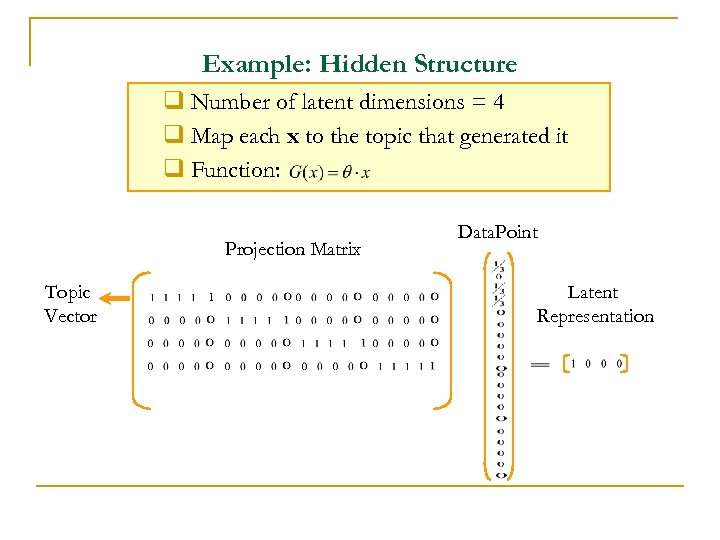 Example: Hidden Structure q Number of latent dimensions = 4 q Map each x to the topic that generated it q Function: Projection Matrix Topic Vector 1 Data. Point Latent Representation
Example: Hidden Structure q Number of latent dimensions = 4 q Map each x to the topic that generated it q Function: Projection Matrix Topic Vector 1 Data. Point Latent Representation
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
 Classical Setting Principal Components Analysis q Rows of theta as a ‘basis’: q Example generated by: T 1 T 2 T 3 T 4 q Low Reconstruction Error:
Classical Setting Principal Components Analysis q Rows of theta as a ‘basis’: q Example generated by: T 1 T 2 T 3 T 4 q Low Reconstruction Error:
 Minimum Error Formulation Approximate high dimensional x with low dimensional x‘ Orthonormal basis Error: Solution Data covariance Distorsion
Minimum Error Formulation Approximate high dimensional x with low dimensional x‘ Orthonormal basis Error: Solution Data covariance Distorsion
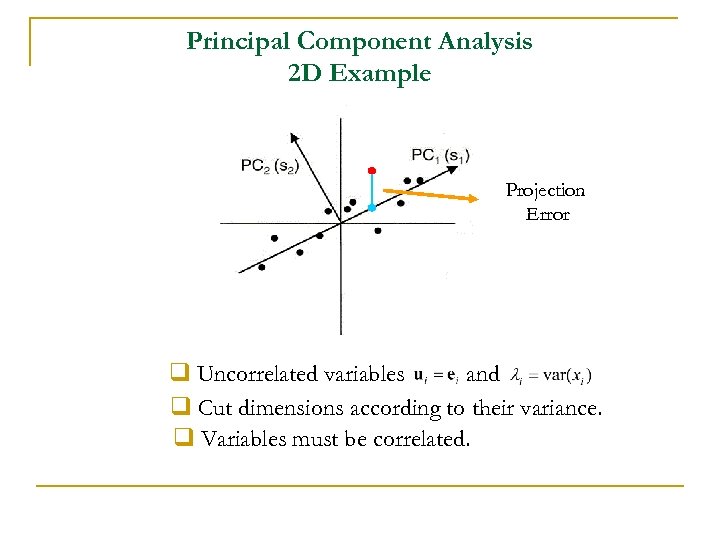 Principal Component Analysis 2 D Example Projection Error q Uncorrelated variables and q Cut dimensions according to their variance. q Variables must be correlated.
Principal Component Analysis 2 D Example Projection Error q Uncorrelated variables and q Cut dimensions according to their variance. q Variables must be correlated.
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
![Partial Supervision Setting [Ando & Zhang JMLR 2005] Unlabeled Dataset + Partial Supervision Create Partial Supervision Setting [Ando & Zhang JMLR 2005] Unlabeled Dataset + Partial Supervision Create](https://present5.com/presentation/f3923e4ea1e6c63a03fc0de37b3951ac/image-15.jpg) Partial Supervision Setting [Ando & Zhang JMLR 2005] Unlabeled Dataset + Partial Supervision Create Auxiliary Tasks Structure Learning
Partial Supervision Setting [Ando & Zhang JMLR 2005] Unlabeled Dataset + Partial Supervision Create Auxiliary Tasks Structure Learning
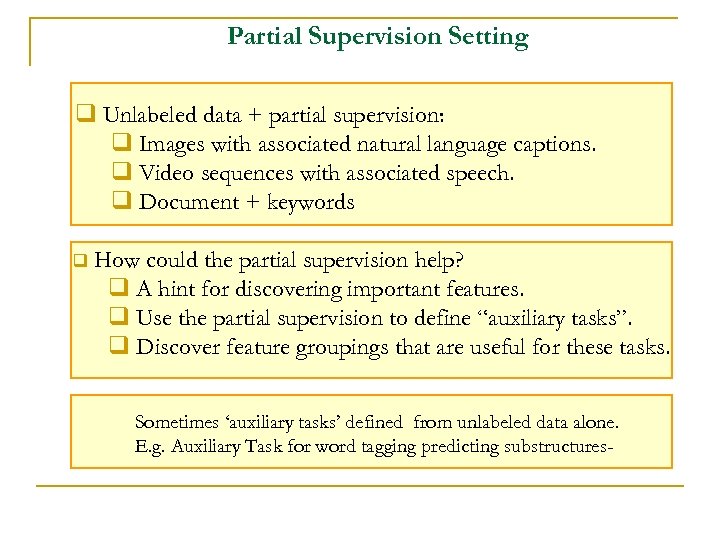 Partial Supervision Setting q Unlabeled data + partial supervision: q Images with associated natural language captions. q Video sequences with associated speech. q Document + keywords q How could the partial supervision help? q A hint for discovering important features. q Use the partial supervision to define “auxiliary tasks”. q Discover feature groupings that are useful for these tasks. Sometimes ‘auxiliary tasks’ defined from unlabeled data alone. E. g. Auxiliary Task for word tagging predicting substructures-
Partial Supervision Setting q Unlabeled data + partial supervision: q Images with associated natural language captions. q Video sequences with associated speech. q Document + keywords q How could the partial supervision help? q A hint for discovering important features. q Use the partial supervision to define “auxiliary tasks”. q Discover feature groupings that are useful for these tasks. Sometimes ‘auxiliary tasks’ defined from unlabeled data alone. E. g. Auxiliary Task for word tagging predicting substructures-
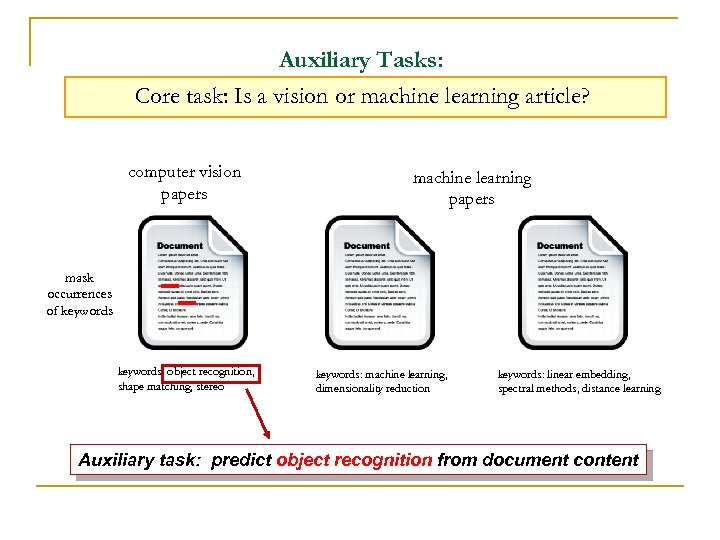 Auxiliary Tasks: Core task: Is a vision or machine learning article? computer vision papers machine learning papers mask occurrences of keywords: object recognition, shape matching, stereo keywords: machine learning, dimensionality reduction keywords: linear embedding, spectral methods, distance learning Auxiliary task: predict object recognition from document content
Auxiliary Tasks: Core task: Is a vision or machine learning article? computer vision papers machine learning papers mask occurrences of keywords: object recognition, shape matching, stereo keywords: machine learning, dimensionality reduction keywords: linear embedding, spectral methods, distance learning Auxiliary task: predict object recognition from document content
 Auxiliary Tasks
Auxiliary Tasks
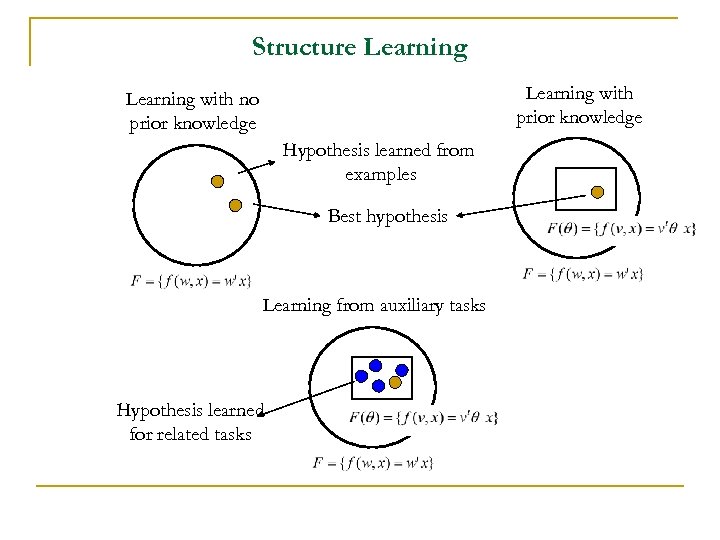 Structure Learning with prior knowledge Learning with no prior knowledge Hypothesis learned from examples Best hypothesis Learning from auxiliary tasks Hypothesis learned for related tasks
Structure Learning with prior knowledge Learning with no prior knowledge Hypothesis learned from examples Best hypothesis Learning from auxiliary tasks Hypothesis learned for related tasks
 Learning Good Hypothesis Spaces n n n Class of linear predictors: is an h by d matrix of structural parameters. Goal: Find the parameters and shared that minimizes the joint loss. Shared Class of linear predictors: parameters Problem specific parameters is an h by d matrix of structural parameters. Goal: Find the parameters and shared that minimizes the joint loss. Loss on training set
Learning Good Hypothesis Spaces n n n Class of linear predictors: is an h by d matrix of structural parameters. Goal: Find the parameters and shared that minimizes the joint loss. Shared Class of linear predictors: parameters Problem specific parameters is an h by d matrix of structural parameters. Goal: Find the parameters and shared that minimizes the joint loss. Loss on training set
 Algorithm Step 1: Train classifiers for auxiliary tasks.
Algorithm Step 1: Train classifiers for auxiliary tasks.
 by taking the first h eigenvectors of Covariance Matrix: Linear subspace of dimension h; a good low dimensional approximation to the space of coefficients.
by taking the first h eigenvectors of Covariance Matrix: Linear subspace of dimension h; a good low dimensional approximation to the space of coefficients.
 Algorithm Step 3: Training on the core task Project data: Equivalent to training core task on the original d dimensional space with parameters constraints:
Algorithm Step 3: Training on the core task Project data: Equivalent to training core task on the original d dimensional space with parameters constraints:
 Example Object = { letter, letter } n An object ab. C
Example Object = { letter, letter } n An object ab. C
 Example n The same object seen in a different font Abc
Example n The same object seen in a different font Abc
 Example n The same object seen in a different font ABc
Example n The same object seen in a different font ABc
 Example n The same object seen in a different font ab. C
Example n The same object seen in a different font ab. C
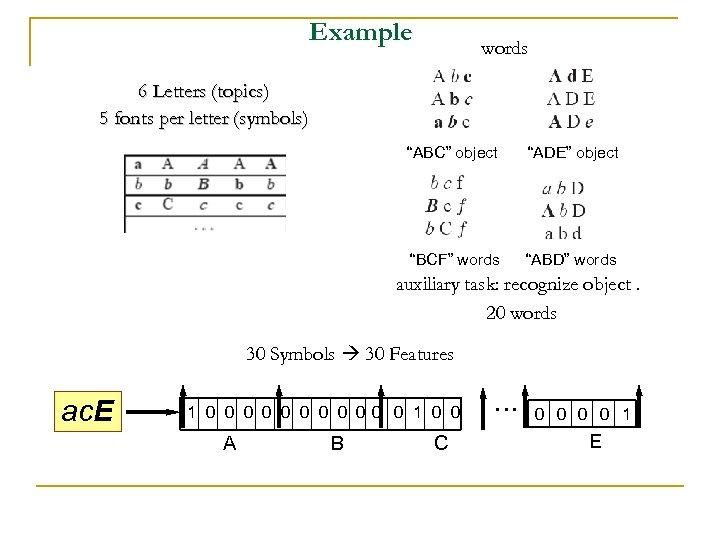 Example words 6 Letters (topics) 5 fonts per letter (symbols) “ABC” object “ADE” object “BCF” words “ABD” words auxiliary task: recognize object. 20 words 30 Symbols 30 Features ac. E 1 0 0 0 0 00 0 1 0 0 A B C . . . 0 0 1 E
Example words 6 Letters (topics) 5 fonts per letter (symbols) “ABC” object “ADE” object “BCF” words “ABD” words auxiliary task: recognize object. 20 words 30 Symbols 30 Features ac. E 1 0 0 0 0 00 0 1 0 0 A B C . . . 0 0 1 E
 PCA on Data can not recover lantent structure Covariance DATA
PCA on Data can not recover lantent structure Covariance DATA
 PCA on Coefficients can recover latent structure Auxiliary Tasks W Features i. e. fonts Topics i. e Letters Parameters for object BCD
PCA on Coefficients can recover latent structure Auxiliary Tasks W Features i. e. fonts Topics i. e Letters Parameters for object BCD
 PCA on Coefficients can recover latent structure Features i. e. fonts Covariance W Features i. e. fonts Each Block of Correlated Variables corresponds to a Latent Topic
PCA on Coefficients can recover latent structure Features i. e. fonts Covariance W Features i. e. fonts Each Block of Correlated Variables corresponds to a Latent Topic
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
 News domain figure skating ice hockey golden globes grammys Dataset: News images from Reuters web-site. Problem: Predicting news topics from images.
News domain figure skating ice hockey golden globes grammys Dataset: News images from Reuters web-site. Problem: Predicting news topics from images.
 Learning visual representations using images with captions The Italian team celebrate their gold medal win during the flower ceremony after the final round of the men's team pursuit speedskating at Oval Lingotto during the 2006 Winter Olympics. Former U. S. President Bill Clinton speaks during a joint news conference with Pakistan's Prime Minister Shaukat Aziz at Prime Minister house in Islamabad. Diana and Marshall Reed leave the funeral of miner David Lewis in Philippi, West Virginia on January 8, 2006. Lewis was one of 12 miners who died in the Sago Mine. Auxiliary task: predict “ team ” from image content Jim Scherr, the US Olympic Committee's chief executive officer seen here in 2004, said his group is watching the growing scandal and keeping informed about the NHL's investigation into Rick Tocchet, U. S. director Stephen Gaghan and his girlfriend Daniela Unruh arrive on the red carpet for the screening of his film 'Syriana' which runs out of competition at the 56 th Berlinale International Film Festival. Senior Hamas leader Khaled Meshaal (2 nd-R), is surrounded by his bodyguards after a news conference in Cairo February 8, 2006.
Learning visual representations using images with captions The Italian team celebrate their gold medal win during the flower ceremony after the final round of the men's team pursuit speedskating at Oval Lingotto during the 2006 Winter Olympics. Former U. S. President Bill Clinton speaks during a joint news conference with Pakistan's Prime Minister Shaukat Aziz at Prime Minister house in Islamabad. Diana and Marshall Reed leave the funeral of miner David Lewis in Philippi, West Virginia on January 8, 2006. Lewis was one of 12 miners who died in the Sago Mine. Auxiliary task: predict “ team ” from image content Jim Scherr, the US Olympic Committee's chief executive officer seen here in 2004, said his group is watching the growing scandal and keeping informed about the NHL's investigation into Rick Tocchet, U. S. director Stephen Gaghan and his girlfriend Daniela Unruh arrive on the red carpet for the screening of his film 'Syriana' which runs out of competition at the 56 th Berlinale International Film Festival. Senior Hamas leader Khaled Meshaal (2 nd-R), is surrounded by his bodyguards after a news conference in Cairo February 8, 2006.
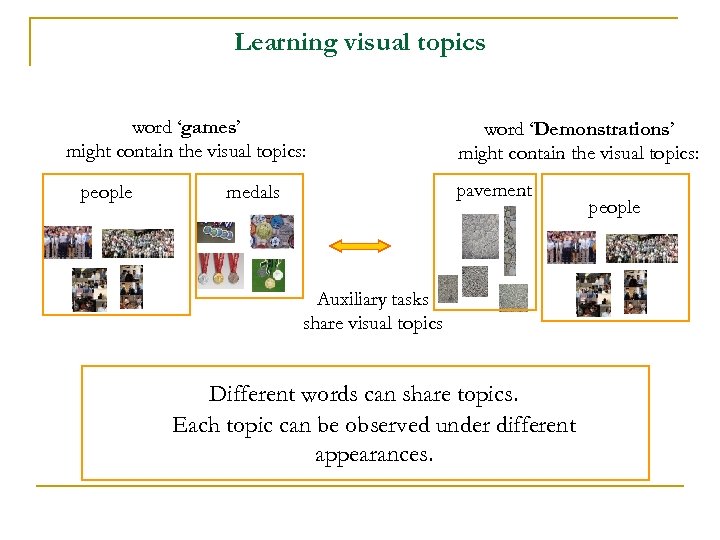 Learning visual topics word ‘games’ might contain the visual topics: people word ‘Demonstrations’ might contain the visual topics: pavement medals Auxiliary tasks share visual topics Different words can share topics. Each topic can be observed under different appearances. people
Learning visual topics word ‘games’ might contain the visual topics: people word ‘Demonstrations’ might contain the visual topics: pavement medals Auxiliary tasks share visual topics Different words can share topics. Each topic can be observed under different appearances. people
 Experiments Results
Experiments Results
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
 Chunking • Named entity chunking Jane lives in New York and works for Bank of New PER LOC ORG • Syntactic chunking But economists in Europe failed to predict that … NP PP NP VP SBAR Data points: word occurrences Labels: Begin-PER, Inside-PER, Begin-LOC, …, Out
Chunking • Named entity chunking Jane lives in New York and works for Bank of New PER LOC ORG • Syntactic chunking But economists in Europe failed to predict that … NP PP NP VP SBAR Data points: word occurrences Labels: Begin-PER, Inside-PER, Begin-LOC, …, Out
 Example input vector representation … lives in New York … 1 curr-“New” 1 curr-“in” left-“in” 1 left-“lives” 1 1 right-“New” 1 right-“York” input vector X • High-dimensional vectors. • Most entries are 0.
Example input vector representation … lives in New York … 1 curr-“New” 1 curr-“in” left-“in” 1 left-“lives” 1 1 right-“New” 1 right-“York” input vector X • High-dimensional vectors. • Most entries are 0.
 Algorithmic Procedure 1. Create m auxiliary problems. 2. Assign auxiliary labels to unlabeled data. 3. Compute (shared structure) by joint empirical risk minimization over all the auxiliary problems. 4. Fix , and minimize empirical risk on the labeled data for the target task. Predictor: Additiona l features
Algorithmic Procedure 1. Create m auxiliary problems. 2. Assign auxiliary labels to unlabeled data. 3. Compute (shared structure) by joint empirical risk minimization over all the auxiliary problems. 4. Fix , and minimize empirical risk on the labeled data for the target task. Predictor: Additiona l features
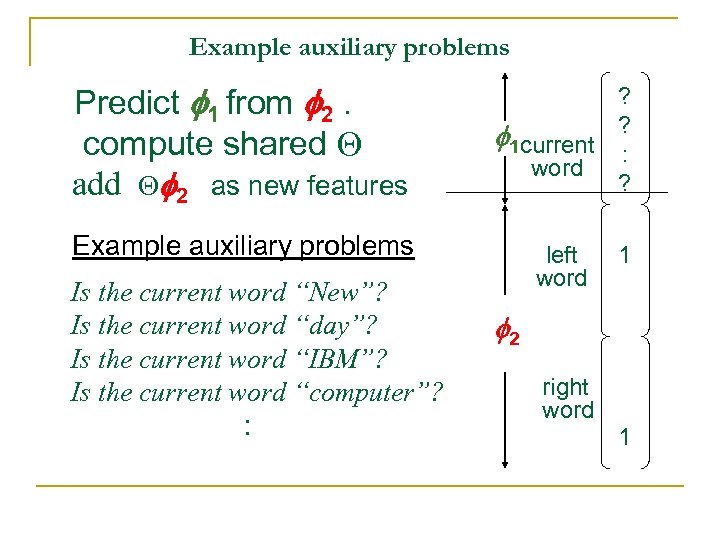 Example auxiliary problems Predict 1 from 2. compute shared Q add Q 2 as new features ? 1 current ? : word ? Example auxiliary problems left word Is the current word “New”? Is the current word “day”? Is the current word “IBM”? Is the current word “computer”? : 1 2 right word 1
Example auxiliary problems Predict 1 from 2. compute shared Q add Q 2 as new features ? 1 current ? : word ? Example auxiliary problems left word Is the current word “New”? Is the current word “day”? Is the current word “IBM”? Is the current word “computer”? : 1 2 right word 1
 Experiments (Co. NLL-03 named entity) n n 4 classes: LOC, ORG, PER, MISC Labeled data: News documents. 204 K words (English), 206 K words (German) Unlabeled data: 27 M words (English), 35 M words (German) Features: A slight modification of ZJ 03. Words, POS, char types, 4 chars at the beginning/ending in a 5 word window; words in a 3 -chunk window; labels assigned to two words on the left, bi-gram of the current word and left label; labels assigned to previous occurrences of the current word. No gazetteer. No hand-crafted resources.
Experiments (Co. NLL-03 named entity) n n 4 classes: LOC, ORG, PER, MISC Labeled data: News documents. 204 K words (English), 206 K words (German) Unlabeled data: 27 M words (English), 35 M words (German) Features: A slight modification of ZJ 03. Words, POS, char types, 4 chars at the beginning/ending in a 5 word window; words in a 3 -chunk window; labels assigned to two words on the left, bi-gram of the current word and left label; labels assigned to previous occurrences of the current word. No gazetteer. No hand-crafted resources.
 Auxiliary problems # of aux. Auxiliary labels problem s 1000 Previous words 1000 Current words 1000 Next words Features used for learning auxiliary problems All but previous words All but current words All but next words 300 auxiliary problems.
Auxiliary problems # of aux. Auxiliary labels problem s 1000 Previous words 1000 Current words 1000 Next words Features used for learning auxiliary problems All but previous words All but current words All but next words 300 auxiliary problems.
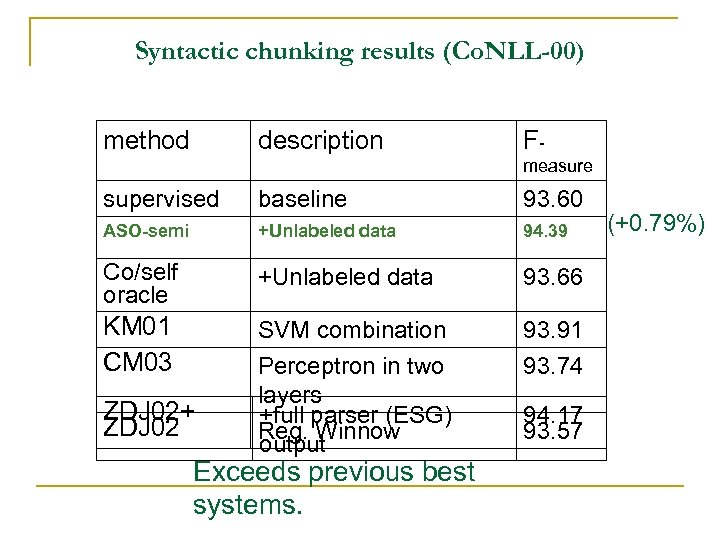 Syntactic chunking results (Co. NLL-00) method description Fmeasure supervised baseline 93. 60 ASO-semi +Unlabeled data 94. 39 Co/self oracle +Unlabeled data 93. 66 KM 01 CM 03 SVM combination Perceptron in two layers +full parser (ESG) Reg. Winnow output 93. 91 93. 74 ZDJ 02+ ZDJ 02 Exceeds previous best systems. 94. 17 93. 57 (+0. 79%)
Syntactic chunking results (Co. NLL-00) method description Fmeasure supervised baseline 93. 60 ASO-semi +Unlabeled data 94. 39 Co/self oracle +Unlabeled data 93. 66 KM 01 CM 03 SVM combination Perceptron in two layers +full parser (ESG) Reg. Winnow output 93. 91 93. 74 ZDJ 02+ ZDJ 02 Exceeds previous best systems. 94. 17 93. 57 (+0. 79%)
 Other experiments Confirmed effectiveness on: n n POS tagging Text categorization (2 standard corpora)
Other experiments Confirmed effectiveness on: n n POS tagging Text categorization (2 standard corpora)
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
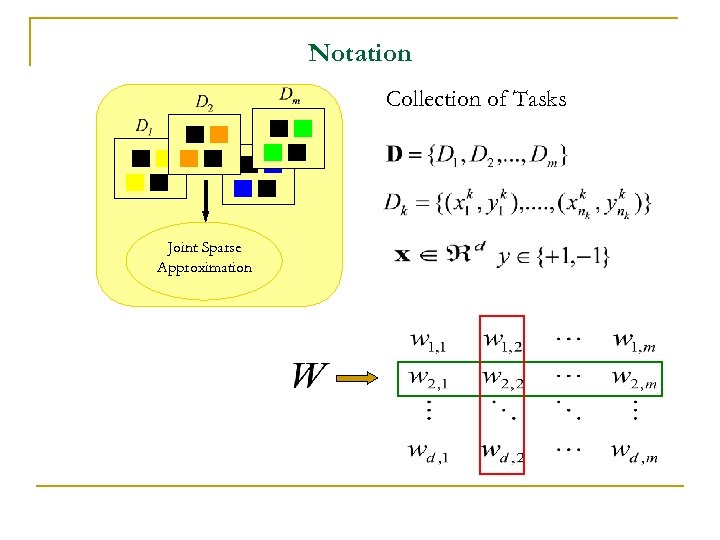 Notation Collection of Tasks Joint Sparse Approximation
Notation Collection of Tasks Joint Sparse Approximation
 Single Task Sparse Approximation q Consider learning a single sparse linear classifier of the form: q We want a few features with non-zero coefficients q Recent work suggests to use L 1 regularization: Classification error L 1 penalizes non-sparse solutions q Donoho [2004] proved (in a regression setting) that the solution with smallest L 1 norm is also the sparsest solution.
Single Task Sparse Approximation q Consider learning a single sparse linear classifier of the form: q We want a few features with non-zero coefficients q Recent work suggests to use L 1 regularization: Classification error L 1 penalizes non-sparse solutions q Donoho [2004] proved (in a regression setting) that the solution with smallest L 1 norm is also the sparsest solution.
 Joint Sparse Approximation q Setting : Joint Sparse Approximation Average Loss on training set k penalizes solutions that utilize too many features
Joint Sparse Approximation q Setting : Joint Sparse Approximation Average Loss on training set k penalizes solutions that utilize too many features
 Joint Regularization Penalty q How do we penalize solutions that use too many features? Coefficients for feature 2 Coefficients for classifier 2 q Would lead to a hard combinatorial problem.
Joint Regularization Penalty q How do we penalize solutions that use too many features? Coefficients for feature 2 Coefficients for classifier 2 q Would lead to a hard combinatorial problem.
![Joint Regularization Penalty q We will use a L 1 -∞ norm [Tropp 2006] Joint Regularization Penalty q We will use a L 1 -∞ norm [Tropp 2006]](https://present5.com/presentation/f3923e4ea1e6c63a03fc0de37b3951ac/image-51.jpg) Joint Regularization Penalty q We will use a L 1 -∞ norm [Tropp 2006] q This norm combines: The L∞ norm on each row promotes non-sparsity on the rows. An L 1 norm on the maximum absolute values of the coefficients across tasks promotes sparsity. Share features Use few features q The combination of the two norms results in a solution where only a few features are used but the features used will contribute in solving many classification problems.
Joint Regularization Penalty q We will use a L 1 -∞ norm [Tropp 2006] q This norm combines: The L∞ norm on each row promotes non-sparsity on the rows. An L 1 norm on the maximum absolute values of the coefficients across tasks promotes sparsity. Share features Use few features q The combination of the two norms results in a solution where only a few features are used but the features used will contribute in solving many classification problems.
 Joint Sparse Approximation q Using the L 1 -∞ norm we can rewrite our objective function as: q For any convex loss this is a convex objective. q For the hinge loss: the optimization problem can be expressed as a linear program.
Joint Sparse Approximation q Using the L 1 -∞ norm we can rewrite our objective function as: q For any convex loss this is a convex objective. q For the hinge loss: the optimization problem can be expressed as a linear program.
 Joint Sparse Approximation q Linear program formulation (hinge loss): q Objective: q Max value constraints: and q Slack variables constraints: and
Joint Sparse Approximation q Linear program formulation (hinge loss): q Objective: q Max value constraints: and q Slack variables constraints: and
 An efficient training algorithm q The LP formulation can be optimized using standard LP solvers. q The LP formulation is feasible for small problems but becomes intractable for larger data-sets with thousands of examples and dimensions. q We might want a more general optimization algorithm that can handle arbitrary convex losses. q We developed a simple an efficient global optimization algorithm for training joint models with L 1−∞ constraints. q The total cost is in the order of:
An efficient training algorithm q The LP formulation can be optimized using standard LP solvers. q The LP formulation is feasible for small problems but becomes intractable for larger data-sets with thousands of examples and dimensions. q We might want a more general optimization algorithm that can handle arbitrary convex losses. q We developed a simple an efficient global optimization algorithm for training joint models with L 1−∞ constraints. q The total cost is in the order of:
 Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
Outline Motivation: Low dimensional representations. q Principal Component Analysis. q Structural Learning. q Vision Applications. q NLP Applications. q Joint Sparsity. q Vision Applications. q
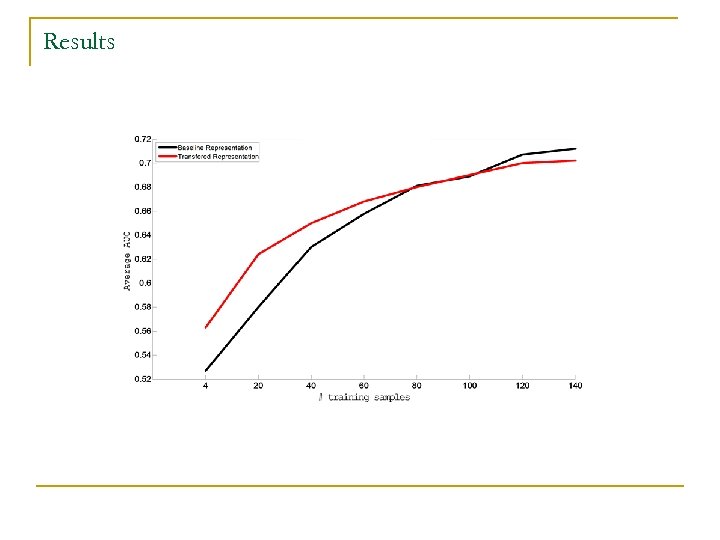
 Super. Bowl Sharon Danish Cartoons Academy Awards Australian Open Grammys Trapped Miners Figure Skating Golden globes Iraq q Train a classifier for the 10 th held out topic using the relevant features R only. q Learn a representation using labeled data from 9 topics. q Learn the matrix W using our transfer algorithm. q Define the set of relevant features to be:
Super. Bowl Sharon Danish Cartoons Academy Awards Australian Open Grammys Trapped Miners Figure Skating Golden globes Iraq q Train a classifier for the 10 th held out topic using the relevant features R only. q Learn a representation using labeled data from 9 topics. q Learn the matrix W using our transfer algorithm. q Define the set of relevant features to be:
 Results
Results
 Future Directions Joint Sparsity Regularization to control inference time. Learning representations for ranking problems.
Future Directions Joint Sparsity Regularization to control inference time. Learning representations for ranking problems.


