Laws of Diminishing returns Numerical example Factor

Laws of Diminishing returns Numerical example

Factor Costs: l l Labour – wages/salaries Land – rent Capital – interest Enterprise - profit

Short and Long run: l Short run – some factors fixed and cannot be increased/reduced l Long Run – time taken to vary all factors of production l Short and long run vary in all industries:

How can these ‘businesses’ increase productivity in the short run? Railways Supermarkets Local Builder

How can these ‘businesses’ increase productivity in the short run? Railways ‘easy’ to increase labour Supermarkets can buy new shelving, hire staff How can they Local Builder increase production in the Long run? new tools, hires assistant And how long is a long run?

How can they increase production in the Long run and how long is a long run? Railways long lead times for new rolling stock – 5 years Supermarkets Open new stores - takes several years Local Builder purchase a new van – takes a couple of months

Diminishing Marginal Returns l Assumptions – some factors fixed (e. g. capital and land) l Adding variable factor –labour Total Product Average Product = TP / Qv (variable factor) Marginal Product = ΔTP/ΔQv l l l

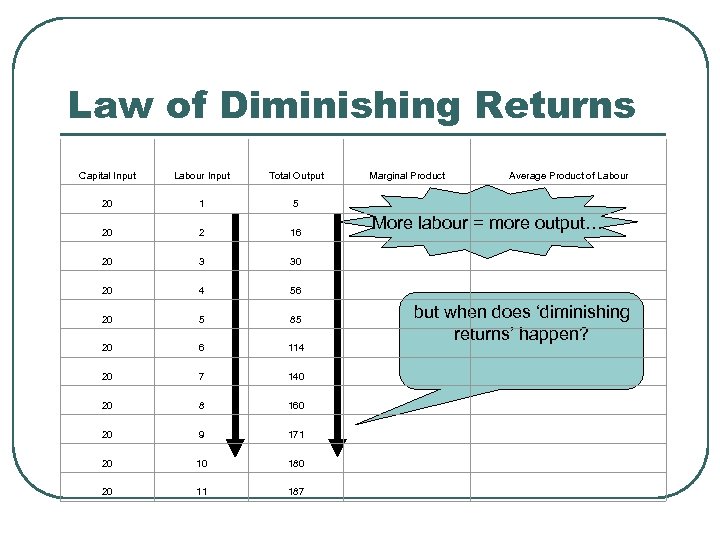Law of Diminishing Returns Capital Input Labour Input Total Output Marginal Product 20 1 5 20 2 16 20 3 30 20 4 56 20 5 85 20 6 114 20 7 140 20 8 160 20 9 171 20 10 180 20 11 187 Average Product of Labour More labour = more output… but when does ‘diminishing returns’ happen?

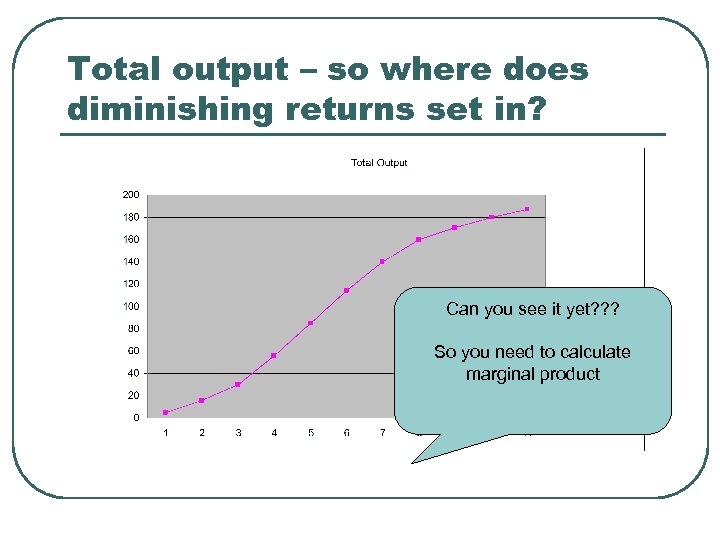Total output – so where does diminishing returns set in? Can you see it yet? ? ? So you need to calculate marginal product

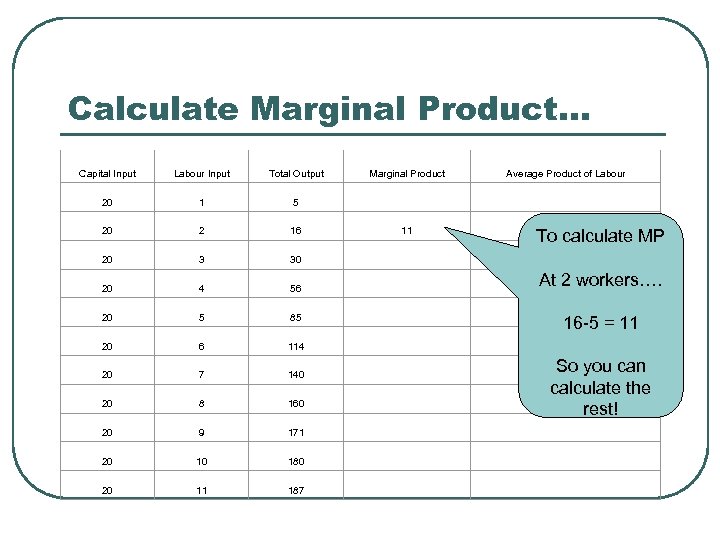Calculate Marginal Product… Capital Input Labour Input Total Output Marginal Product 20 1 5 20 2 16 11 20 3 30 20 4 56 20 5 85 20 6 114 20 7 140 20 8 160 20 9 171 20 10 180 20 11 187 Average Product of Labour To calculate MP At 2 workers…. 16 -5 = 11 So you can calculate the rest!

So where are the increasing returns? Optimal returns? and diminishing returns? Marginal product results… Capital Input Labour Input Total Output Marginal Product 20 1 5 20 2 16 11 20 3 30 14 20 4 56 26 20 5 85 28 20 6 114 29 20 7 140 26 20 8 160 20 20 9 171 11 20 10 180 9 20 11 187 7 Average Product of Labour At low levels of labour input, the fixed factors of production - land capital, tend to be under-utilised which means that each additional worker will have plenty of capital to use and, as a result, marginal product may rise. Beyond a certain point however, the fixed factors of production become scarcer and new workers will not have as much capital to work with so that the capital input becomes diluted among a larger workforce. As a result, the marginal productivity of each worker tends to fall – this is known as the principle of diminishing returns.

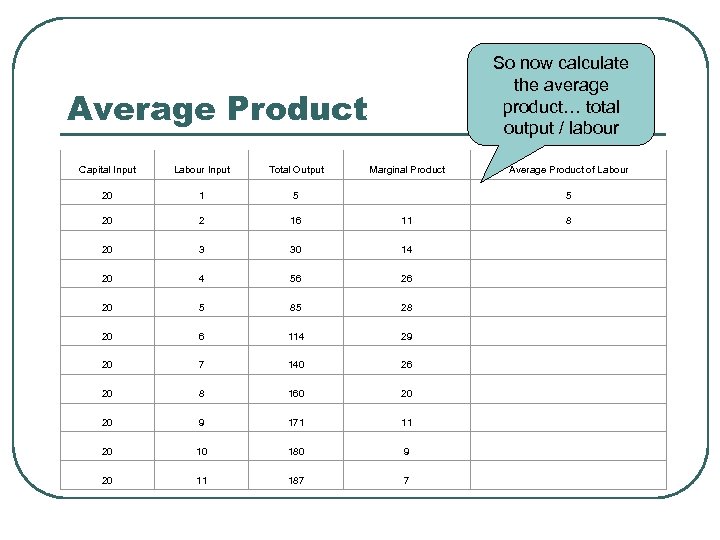So now calculate the average product… total output / labour Average Product Capital Input Labour Input Total Output Marginal Product Average Product of Labour 20 1 5 5 20 2 16 11 8 20 3 30 14 20 4 56 26 20 5 85 28 20 6 114 29 20 7 140 26 20 8 160 20 20 9 171 11 20 10 180 9 20 11 187 7

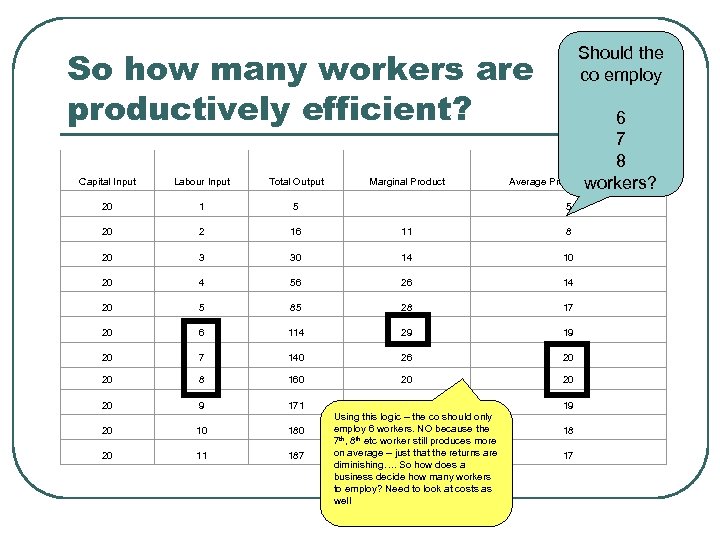Should the co employ So how many workers are productively efficient? 6 7 8 Average Product of Labour workers? Capital Input Labour Input Total Output Marginal Product 20 1 5 5 20 2 16 11 8 20 3 30 14 10 20 4 56 26 14 20 5 85 28 17 20 6 114 29 19 20 7 140 26 20 20 8 160 20 20 20 9 171 20 10 180 20 11 187 11 Using this logic – the co should only employ 6 workers. NO because the 9 7 th, 8 th etc worker still produces more on average – just that the returns are 7 diminishing…. So how does a business decide how many workers to employ? Need to look at costs as well 19 18 17

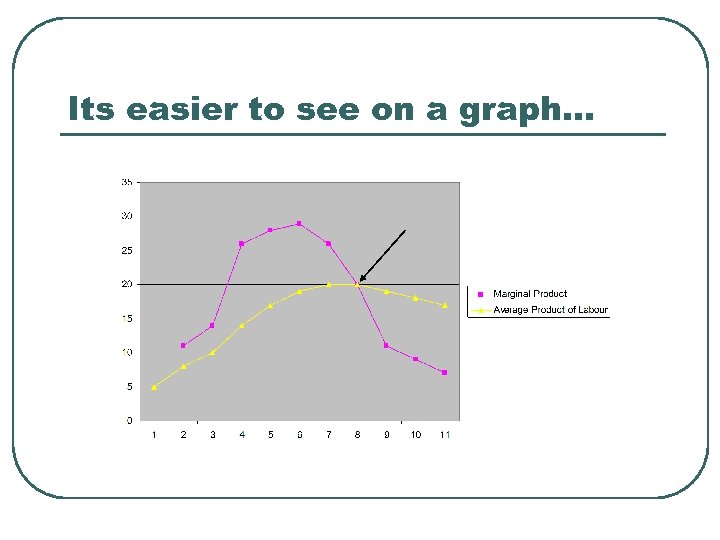Its easier to see on a graph…

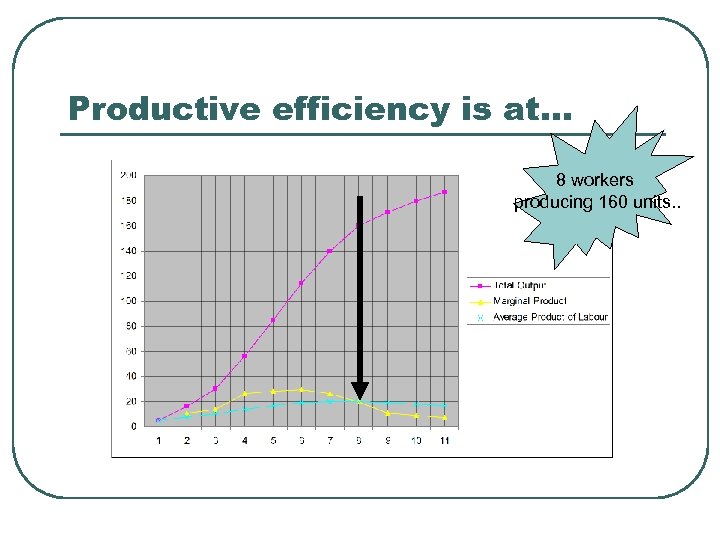Productive efficiency is at… 8 workers producing 160 units. .

So now try an exercise yourself l Don’t panic – this isn’t part of a DR or an essay…… l However, it is the fundamental foundations of what you MUST KNOW for Marginal Costs, productive efficiency and economies of scale…i. e. unit 5!