Lattice Quasi-continuum Phase Transitions Slava Sorkin Department

Lattice, Quasi-continuum & Phase Transitions Slava Sorkin Department of Aerospace Engineering and Mechanics, University of Minnesota

Acknowledgements ● Ellad B. Tadmor, University of Minnesota, Aerospace Engineering and Mechanics ● Ryan Elliot, University of Minnesota, Aerospace Engineering and Mechanics ● Emil Polturak, Physics Department, Technion ● Joan Adler, Physics Department, Technion ● Noam Bernstein, Center for Computational Materials Science and Technology Division Naval Research Laboratory Washington ● Gábor Csányi, University of Cambridge, Engineering Laboratory ● Mitchell Luskin, University of Minnesota, School of Mathematics ● David Ceperley, National Center for Supercomputing Applications at Illinois ● Matteo Cococcioni, University of Minnesota, Chemical Engineering and Materials Science ● David Landau, UGA Physics and Astronomy School

Part I: Multi-scale modelling of materials ● The object of multi-scale modelling is to predict behaviour of materials using theoretical and computational techniques that link across spatial and temporal scales. ● This approach can be considered as an alternative to the empirical methods of today. It offers great opportunities for tomorrow The series of images shows details of the crack tip at the different scales. The atomic-scale mechanism leads to fracture can be seen. This picture compliments of the Naval Research Lab Washington, DC technological advances.

Quasicontinuum (QC) method ● The QC method is one of the best possible strategies devised to couple concurrently micro and macro scales. ● This techniques is a mixed continuum and atomistic approach for simulating the mechanical response of crystalline materials. With QC one can reproduce the results of full atomistic calculation at a fraction of computational cost. A crack tip approaching a grain boundary in a nickel bi-crystal. For frames are shown at increasing level of external load. The snapshots show dislocation emission from the grain boundary, followed by crack extension, and, finally, grain boundary migration toward the crack tip. Taken from www. qcmethod. com

Selection of representative atoms from Quasicontinuum method all the atoms near a dislocation core. Taken from: ”The QC method: overview, application and current directions”, by R. Miller and E. B. Tadmor, JCAMD, 9, 203 ● The main idea of the QC approach is a selective representation of atomic degrees of freedom. A small relevant subset of all atoms is chosen to represent, by proper waiting, the total energy of the system as whole. ● The density of 'representative' atoms is significant in highly deformed regions (dislocation core, crack tip, free surfaces, grain boundaries), and significantly reduced in less deformed regions further away. The fully atomistic regions can evolve with the deformation, during the simulation.

Quasicontinuum method ● The energies of the 'representative' atoms are calculated based on their environment: either by using atomistic methodology, or as befitting to a continuum model. The total energy is calculated without any assumptions beyond the form of inter-atomic potentials. ● With a knowledge of the total energy one can study mechanical response of crystalline material to external load. This can be done by minimizing the total energy with respect to the displacements of the 'representative' atoms. ● Currently, one of the most important direction for our research is to extend the QC method from simple to complex lattices.

Complex lattices ● ● Adapted from http: //www. molecularexpression. com The extension of the QC method to complex lattices permits the study of many technologically important materials such as semiconductors, ferroelectrics, and shape-memory materials. Unit cell of complex lattices contains more than one basis atom per Bravais lattice site. In general, complex lattice can be described as a set of inter-penetrating sub-lattices with the same lattice vectors, but different origin positions.

Complex Lattices ● When a uniform macroscopic deformation is applied, all the sub-lattices undergo the same uniform deformation, but in addition they can slide relative each other. Therefore, to describe complex lattices we increase the number of degrees of freedom to include sub-lattice displacements into account. ● The equilibrium configuration is now obtained by minimizing the total energy with respect to the node and sub-lattice displacements concurrently.

non-essential unit cells Complex Lattices ● To run a QC simulation one has to specify the lattice description by choosing a unit cell. Although this unit cell can be selected in many possible ways, the smallest (essential) unit cell is the typical choice. ● This choice can sometimes be too restrictive: some configurations cannot be described by deforming this essential unit cell. ● To overcome the restriction we decided to replace the essential unit cell by a non-essential one 'on-fly', if necessary. ● During the simulation the phonon spectrum is calculated, and if at least one negative frequency is detected we select a new unit cell.

Uni-axial Stress ● To test the new approach we applied uniaxial stress to the Ni. Ti crystal with a cubic lattice structure. An essential unit cell containing two basis atoms was initially chosen. ● The external load was gradually incremented until the first phonon instability was detected. At this point the two basis atom unit cell was replaced by a four basis atom unit cell. The subsequent minimization led to a drastic increase in the nominal strain; new stable Ir. V phase was identified. The old approach failed to reproduce the proper transition. ● This simple test illustrates necessity of flexible description of the underlying lattice for correct modelling of solid-to-solid transformations. α-

Application ● Using the extended QC method we study properties of Ni. Ti shape-memory alloy. The shape memory alloy 'remembers' its shape: it can be returned to that shape after being deformed, by applying heat to the alloy. ● The shape-memory effect is due to temperature-dependent phase transformation from a low-symmetry martensite to a highsymmetry austenite. ● In order to validate the capability of the QC method to reproduce the shape memory effect http: //everythang. wordpress. com we decided to simulate the shape memory cycle: cooling – deformation - heating.

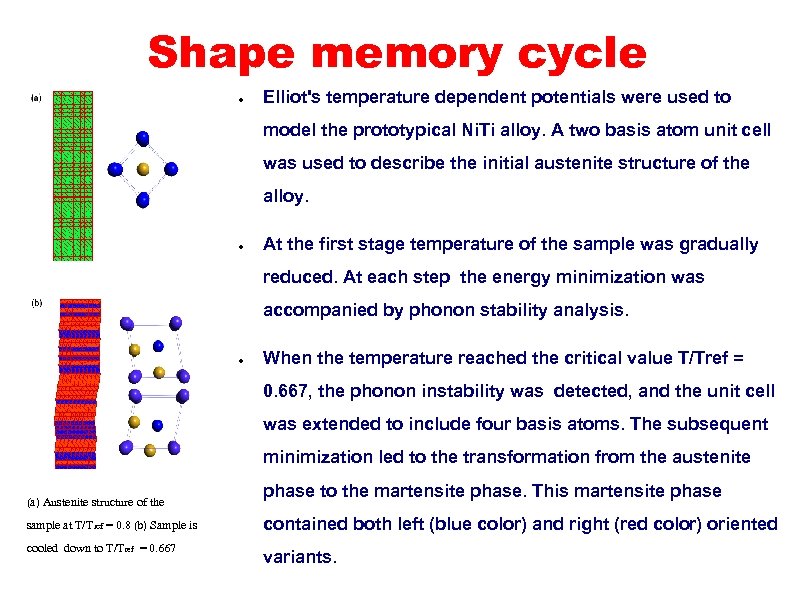Shape memory cycle ● Elliot's temperature dependent potentials were used to model the prototypical Ni. Ti alloy. A two basis atom unit cell was used to describe the initial austenite structure of the alloy. ● At the first stage temperature of the sample was gradually reduced. At each step the energy minimization was accompanied by phonon stability analysis. ● When the temperature reached the critical value T/Tref = 0. 667, the phonon instability was detected, and the unit cell was extended to include four basis atoms. The subsequent minimization led to the transformation from the austenite (a) Austenite structure of the phase to the martensite phase. This martensite phase sample at T/T ref = 0. 8 (b) Sample is contained both left (blue color) and right (red color) oriented cooled down to T/Tref = 0. 667 variants.

Shape memory cycle ● Next, we sheared the sample by displacing the top row nodes to the right. The sample temperature was kept constant: T/Tref = 0. 65 at this stage. ● As the shear progressed all left-oriented martensite elements reversed their orientation. The process started at the bottom and propagated upward. The simulation was terminated when all elements are right-oriented. ● Finally, we heated up the sample to T/Tref = 1. 1; at this temperature a reverse martensite-to-austenite transformation occurred and the original shape of the sample was recovered. (c) The sample is deformed at T/Tref = 0. 65 (d) The sample is heated up to T/T ref = 1. 1 and then cooled down to T/Tref = 0. 8 ● In conclusion, we demonstrated the capability of the extended QC method to simulate shape-memory cycle.

Part II: Mechanical Melting ● Melting is a fundamental process, but despite its common occurrence, understanding this process is still a challenge. ● Over the years, several theories explaining the mechanism of melting have been proposed. This research has evolved to a state where two possible scenarios exist: the first scenario of mechanical melting resulting from lattice instability, and the second scenario of thermodynamic melting which begins at a free surface or at an internal interface (grain boundary, void).

Mechanical Melting ● Mechanical melting occurs when the crystal loses its ability to resist shear. This rigidity catastrophe is caused by vanishing one of the elastic shear moduli. At this point the crystal expands up to a critical specific volume, which is close to that of the melt. This condition determines the mechanical melting temperature Ts of a bulk crystal as it was confirmed in extensive studies of FCC metals. ● The critical volume at which FCC metals melt is independent of the path through phase space by which it is reached: whether one heats the perfect crystal or adds point defects to expand the solid at a constant temperature. ● Our aim was to verify whether this scenario of mechanical melting developed for FCC crystals is also applicable to crystals with BCC lattice structure.

Method and Model ● Mechanical melting transition of vanadium was modeled using molecular dynamics (MD) simulations. ● Since we are interested in the generic features of metallic solids with a BCC structure, the choice of vanadium has no special significance. ● The many-body interaction potential developed by Finnis and Sinclair (FS) was chosen to simulate vanadium: http: //www. neyco. fr/images/vanadium. jpg

Geometry and Boundary Conditions ● ● ● The samples used for the simulations contained 2000 atoms, initially arranged as a perfect BCC crystal. We introduced point defects to the samples either by insertion of extra atoms (self – interstitials) or by removal of atoms from the lattice (vacancies). Since solids can undergo mechanical melting only if they have no free surfaces, periodic boundary conditions were applied in all three directions.

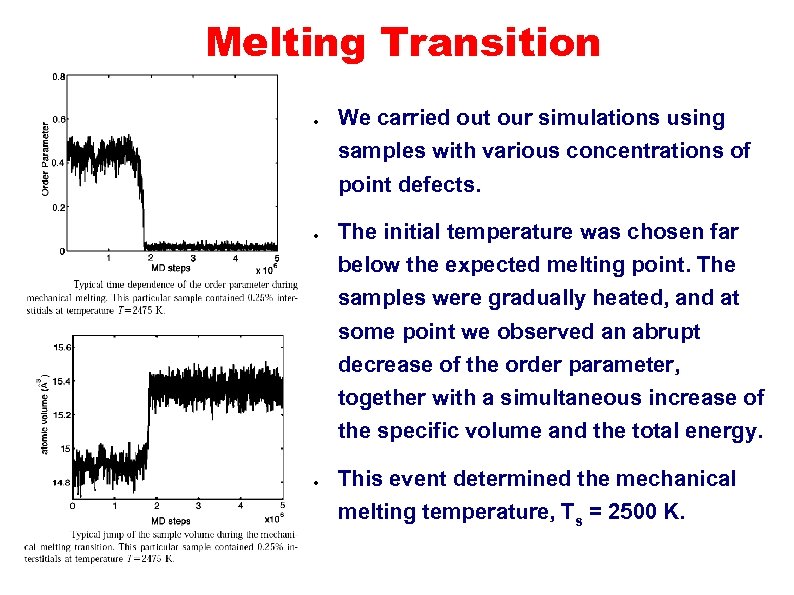Melting Transition ● We carried out our simulations using samples with various concentrations of point defects. ● The initial temperature was chosen far below the expected melting point. The samples were gradually heated, and at some point we observed an abrupt decrease of the order parameter, together with a simultaneous increase of the specific volume and the total energy. ● This event determined the mechanical melting temperature, Ts = 2500 K.

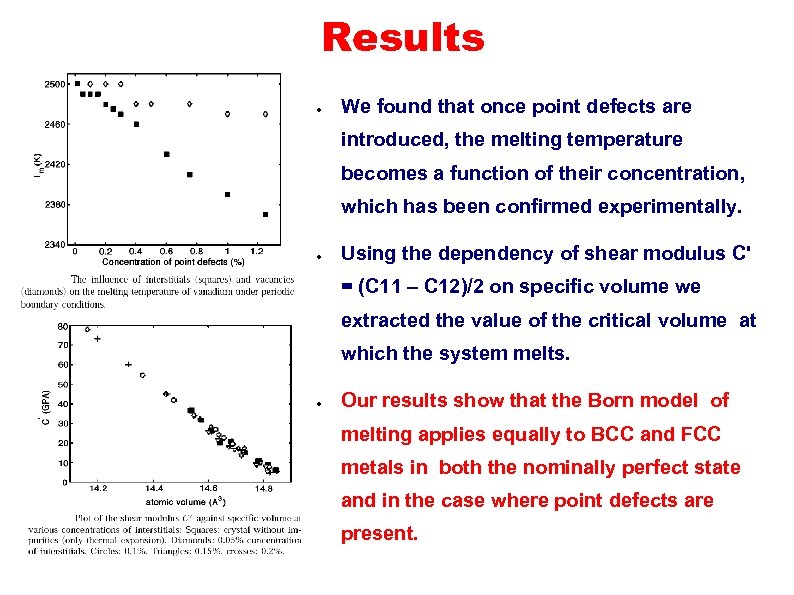Results ● We found that once point defects are introduced, the melting temperature becomes a function of their concentration, which has been confirmed experimentally. ● Using the dependency of shear modulus C' = (C 11 – C 12)/2 on specific volume we extracted the value of the critical volume at which the system melts. ● Our results show that the Born model of melting applies equally to BCC and FCC metals in both the nominally perfect state and in the case where point defects are present.

Part III: Thermodynamic melting

Thermodynamic melting ● The mechanical melting transition cannot be observed in the laboratory since it is preempted by thermodynamic melting transition. Long before the melting temperature is reached a thin quasiliquid layer appears at the free surface. Numerous experiments and computer simulations confirm that FCC metals start to melt from the surface. ● Our primary motivation was to answer the question whether premelting phenomena, extensively studied for FCC metals, are also present in BCC metals. In addition, our goal was to calculate thermodynamic melting temperature, since the temperature Ts = 2500 K at which mechanical melting occurs is far above the experimental value Tm = 2183 K.

Simulation details ● We modelled thermodynamic melting transition of vanadium with a free surface using MD simulations in canonical ensemble. The same FS many-body potential was applied for vanadium. ● A crystal with a surface was modelled as a thick slab with the fixed bottom layers to mimic the presence of the infinite bulk. On top of those layers there were 24 layers in which atoms are free to move. Periodic boundary conditions were imposed along the in-plane (x and y) directions.

Simulation Details ● Three different samples with various low-index surfaces were constructed: V(001), V(011) and V(111). All the samples contained about 3000 atoms initially arranged a perfect BCC crystal. ● Each simulations started from a low-temperature solid, and then the temperature was gradually raised up to a specific value. At this temperature the samples were equilibrated. ● The structural, transport, and energetic properties were measured in thermal equilibrium at various temperatures up to the melting point.

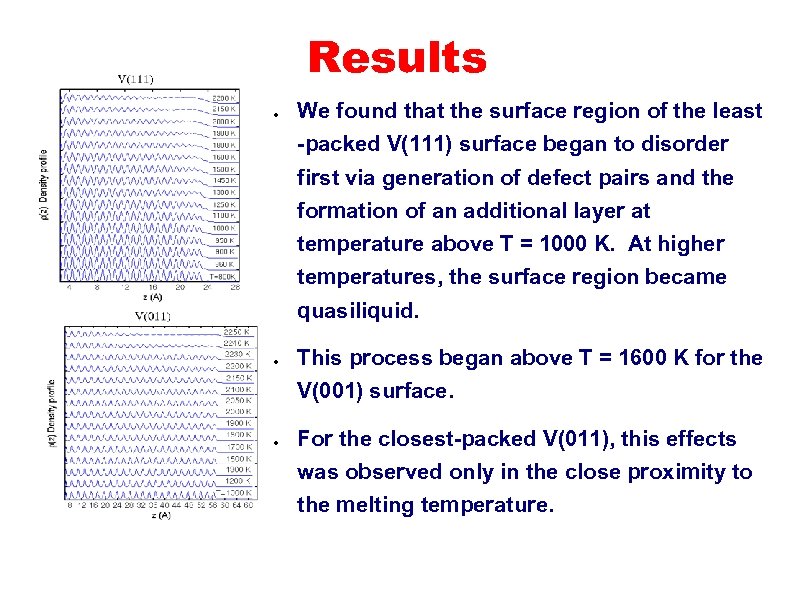Results ● We found that the surface region of the least -packed V(111) surface began to disorder first via generation of defect pairs and the formation of an additional layer at temperature above T = 1000 K. At higher temperatures, the surface region became quasiliquid. ● This process began above T = 1600 K for the V(001) surface. ● For the closest-packed V(011), this effects was observed only in the close proximity to the melting temperature.

Results ● We determined thermodynamic melting temperature of vanadium as Tm = 2220 K, in a good agreement with experimental value Tm = 2183 K. ● The results of our simulations of surface premelting of the BCC metal, vanadium, are similar to the results obtained for various FCC metals, in the sense that the onset of disorder is seen first at the surface with the lowest density.

The End ● For help on the Israel Inter. University Computation Center supercomputers thanks to Dr. Moshe Goldberg, Dr. Anne Weill, Gabi Koren and Jonathan Tal ● For help on the Minnesota Supercomputing Institute machines thanks to Dr. Haoyu Yu, Dr. Shuxia Zhang and Dr. Benjamin Lynch.