Latching forward The statistical modular perspective The Braitenberg

Latching forward

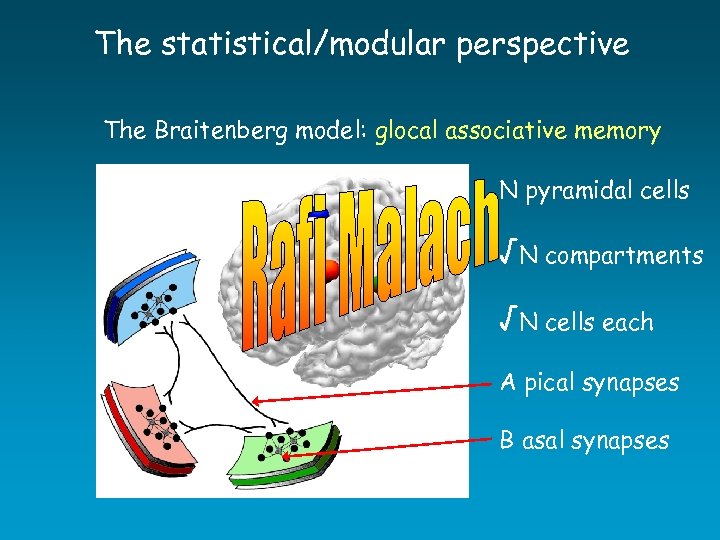
The statistical/modular perspective The Braitenberg model: glocal associative memory N pyramidal cells √N compartments √N cells each A pical synapses B asal synapses

word

A simple a Potts the Reduced to removenetwork updated semantic model (O’Kane glass’ problem (Kropff & Treves, 2005) ‘memory & Treves, 1992) (Fulvi Mari & Treves, 1998) Cortical modules Potts units with dilute Structured long-range connectivity . . but all cortical modules share the same organization… Local attractor S+1 state included “ 0” Potts states (=S) Global global patterns Sparse activitypatterns Sparse Potts patterns p S 2 !! pcc C S? !? !

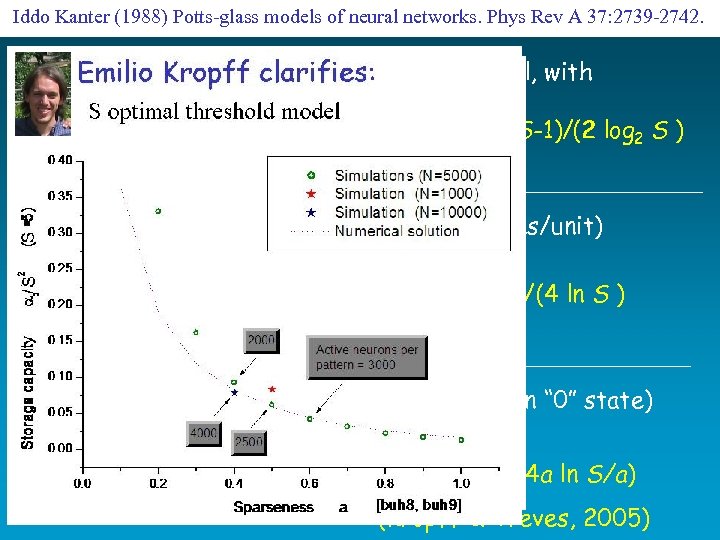
Iddo Kanter (1988) Potts-glass models of neural networks. Phys Rev A 37: 2739 -2742. Potts version of the Hopfield model, with N units S states pc 0. 138 N S (S-1)/(2 log 2 S ) 2 p patterns + dilute connectivity (C connections/unit) I /p = N log 2 S pc C S (S-1)/(4 ln S ) + sparse coding (fraction 1 -a of units in “ 0” state) I /p Na log 2 S/a pc C S (S-1)/(4 a ln S/a) (Kropff & Treves, 2005)

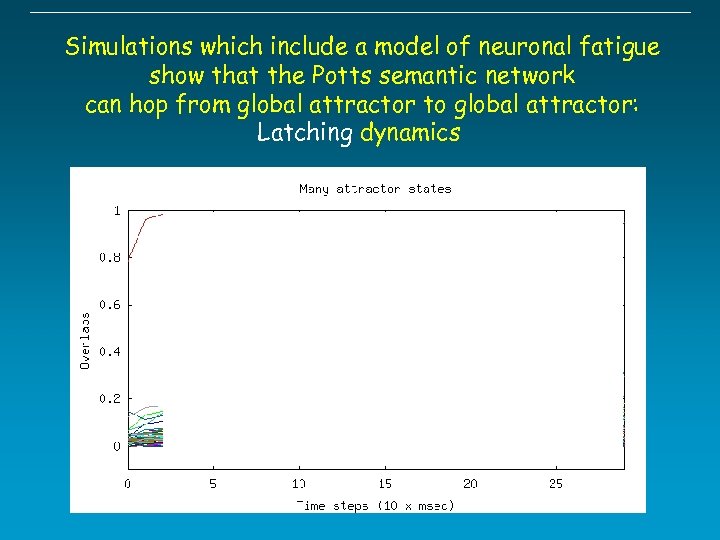
Simulations which include a model of neuronal fatigue show that the Potts semantic network can hop from global attractor to global attractor: Latching dynamics

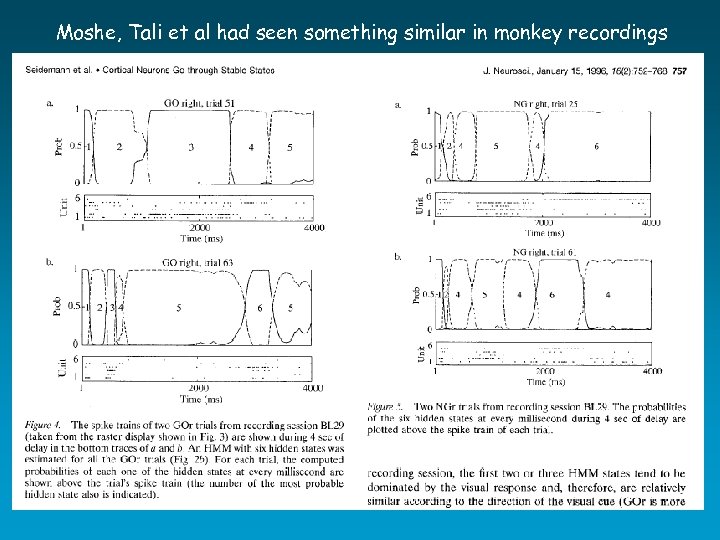
Moshe, Tali et al had seen something similar in monkey recordings

May latching dynamics model a train of thoughts ? (cited by Alistair Knott in his Ph. D Thesis, 1996)

Infinite recursion hypothesis by Hauser, Chomsky & Fitch

Embeddings: . . that John saw Peter help Mary make the children swim… N 1 V 1 N 2 V 2 N 3 V 3 N 4 V 4 . . the realization that the talk they attend has not yet finished makes them weep… N 1 N 2 N 3 V 3 V 2 V 1 (palindrome, or stack memory). . dat Jan Piet Marie de kinderen zag helpen laten zwemmen… N 1 N 2 N 3 N 4 V 1 V 2 V 3 V 4 (interleaving, or queue memory) Finite recursion, it seems… Language is therefore based on a recursive generative procedure that takes elementary word-like elements from some store, call it the lexicon, and applies repeatedly to yield structured expressions, without bound […] Notice that there is no room in this picture for any precursors to language – say a language-like system with only short sentences. There is no rationale for postulation of such a system: to go from seven-word sentences to the discrete infinity of human language requires emergence of the same recursive procedure as to go from zero to infinity, and there is of course no direct evidence for such “protolanguages. ” NC, May 14, 2008

The fluctuation-dissipation theorem applied to working memory correlations among memories fluctuate memory dissipates max embedding depth P(cμν)≈[1/√(2π)]exp-(cμν/σ)2/2 digit span (with a multivariate Gaussian distribution) ? ( 3 or 4 ) x 2 ≈ 7 ± 2 ≈ √ 2 ________________ σ ln(p/√ 2π) assuming binding by synaptic facilitation

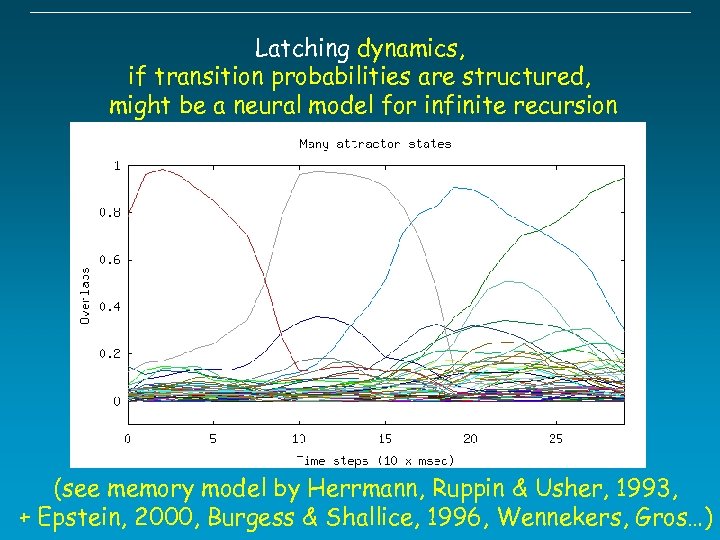
Latching dynamics, if transition probabilities are structured, might be a neural model for infinite recursion (see memory model by Herrmann, Ruppin & Usher, 1993, + Epstein, 2000, Burgess & Shallice, 1996, Wennekers, Gros…)

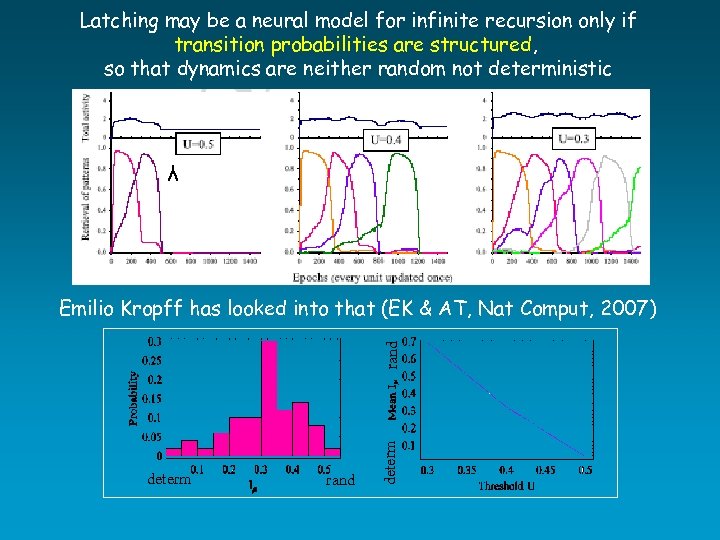
Latching may be a neural model for infinite recursion only if transition probabilities are structured, so that dynamics are neither random not deterministic λ determ rand Emilio Kropff has looked into that (EK & AT, Nat Comput, 2007)

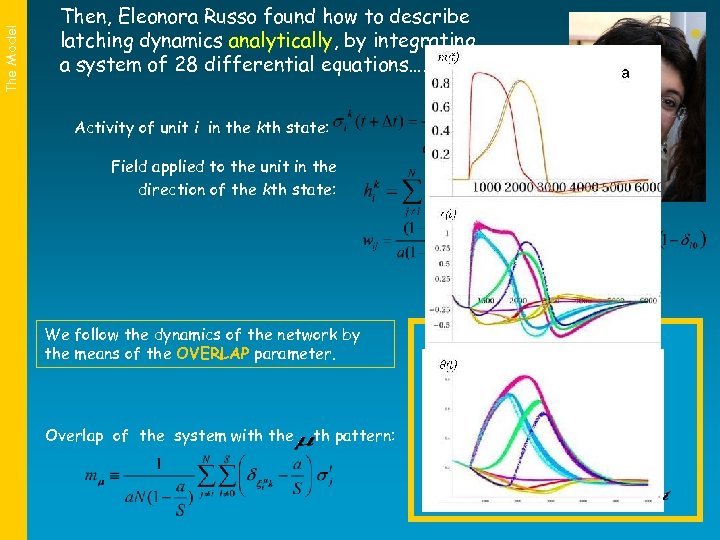
The Model Then, Eleonora Russo found how to describe latching dynamics analytically, by integrating a system of 28 differential equations…. Activity of unit i in the kth state: Field applied to the unit in the direction of the kth state: We follow the dynamics of the network by the means of the OVERLAP parameter. Overlap of the system with the th pattern:

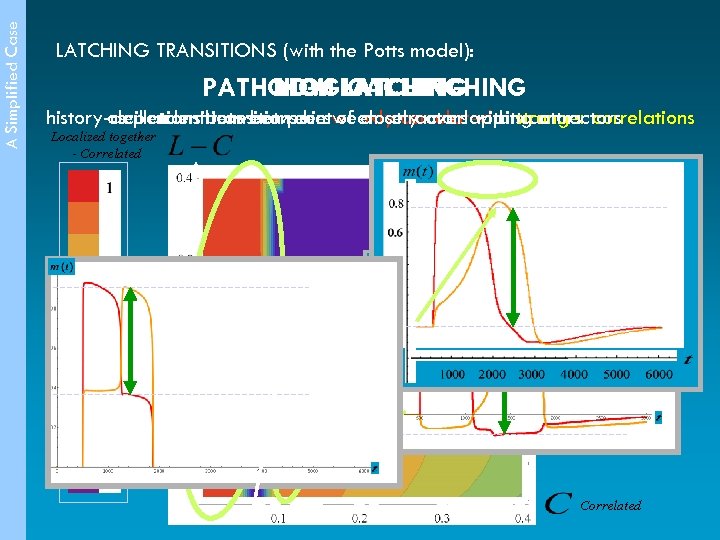
A Simplified Case LATCHING TRANSITIONS (with the Potts model): HIGH LATCHING PATHOLOGICAL LATCHING LOW LATCHING history-dependentbetween pairs weakly correlated attractors correlations oscillations transitions between attractors with stronger transitions between of closely overlapping attractors Localized together - Correlated C ≈ a/S Correlated

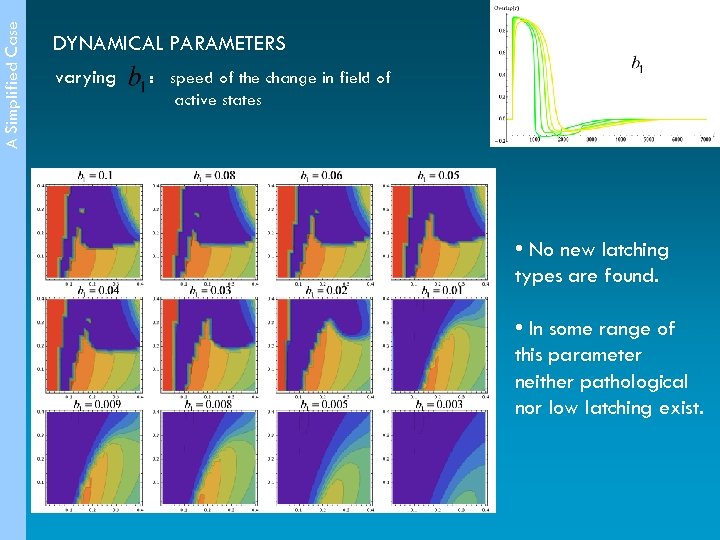
A Simplified Case DYNAMICAL PARAMETERS varying : speed of the change in field of active states • No new latching types are found. • In some range of this parameter neither pathological nor low latching exist.

A Simplified Case A First Conclusion: § three types of latching transitions are present for different correlation levels: • transitions between weakly correlated attractors, • history-dependent transitions between attractors with a stronger correlation, • oscillations between pairs of closely overlapping attractors. § in some regions of the dynamical parameter space not all the three transition types are present.

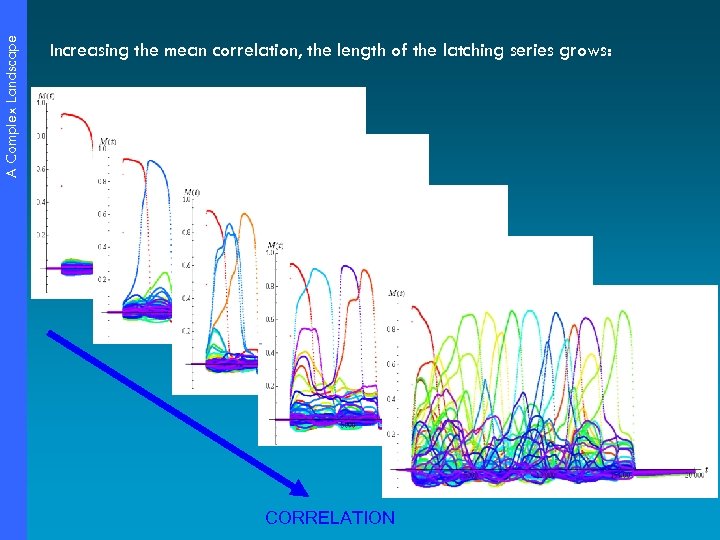
A Complex Landscape Increasing the mean correlation, the length of the latching series grows: CORRELATION

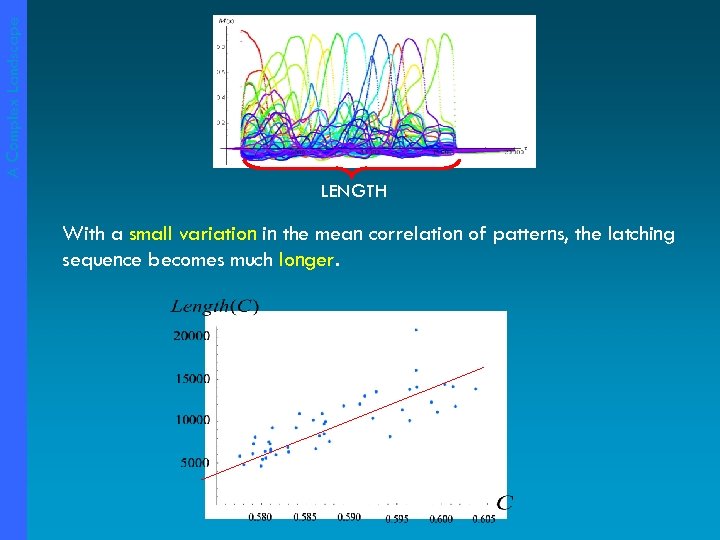
A Complex Landscape LENGTH With a small variation in the mean correlation of patterns, the latching sequence becomes much longer.

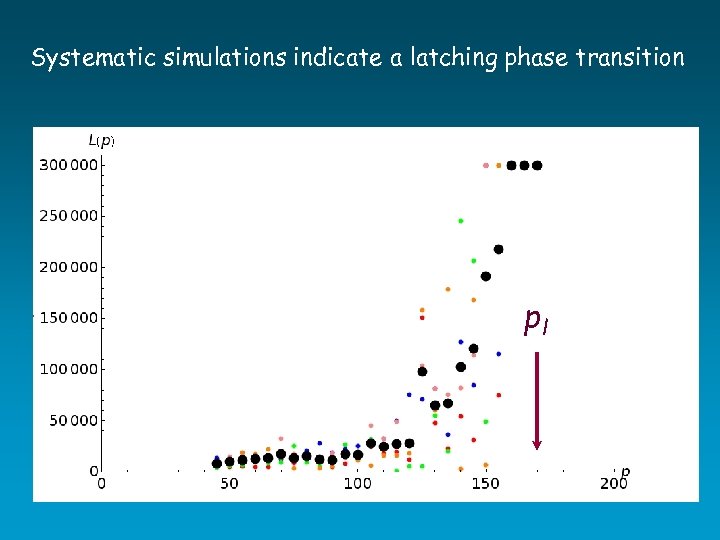
Systematic simulations indicate a latching phase transition pl pl

Back to the analysis, to confirm the crucial quantitative relationships, e. g. that in a multi-factor coding model (with correlated patterns) pc C S 2 ? + pl S ? (see EK & AT, HFSP Journal, 2007)

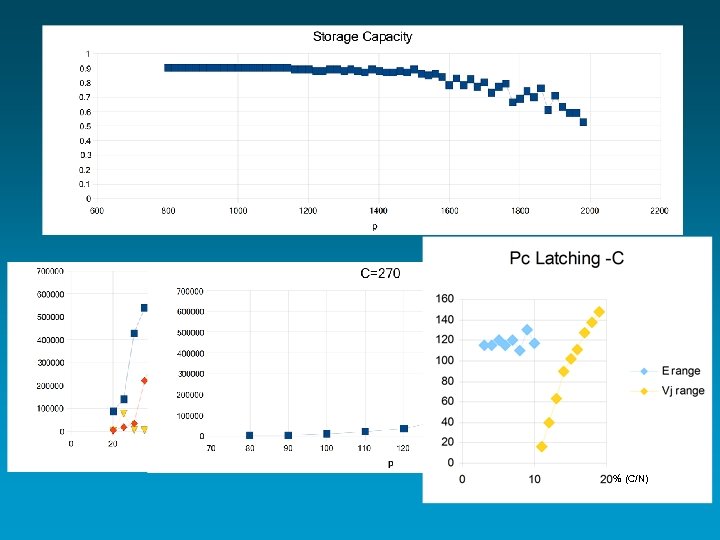
% (C/N)

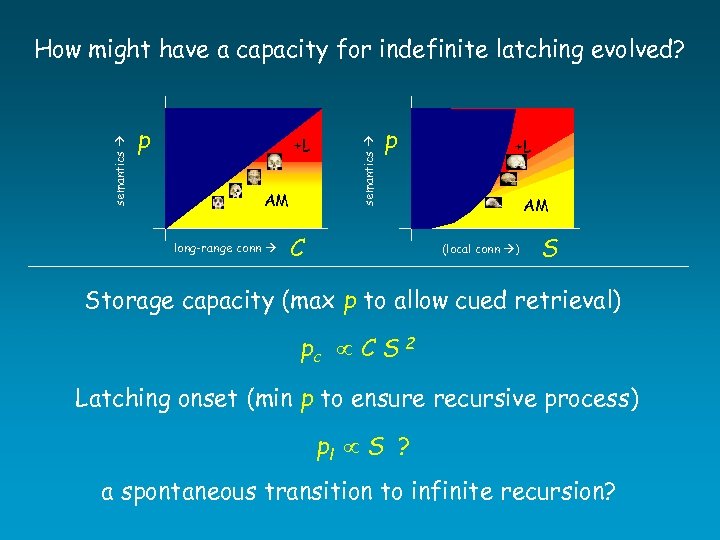
p +L AM long-range conn semantics How might have a capacity for indefinite latching evolved? p C +L AM (local conn ) S Storage capacity (max p to allow cued retrieval) pc C S 2 Latching onset (min p to ensure recursive process) pl S ? a spontaneous transition to infinite recursion?

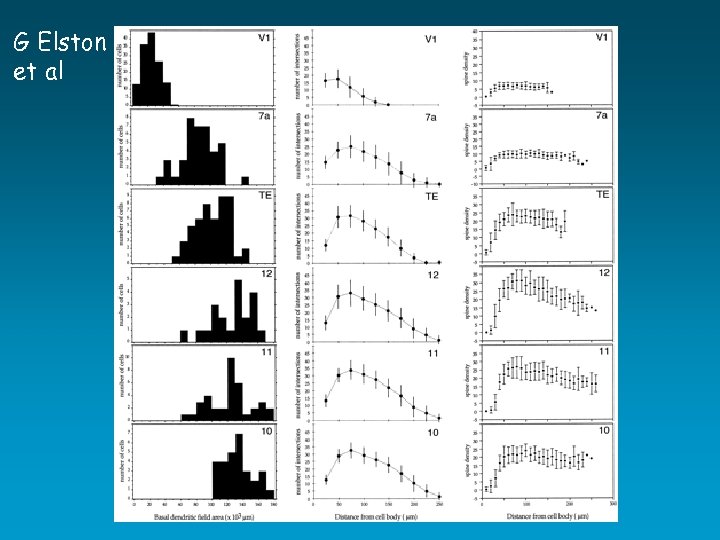
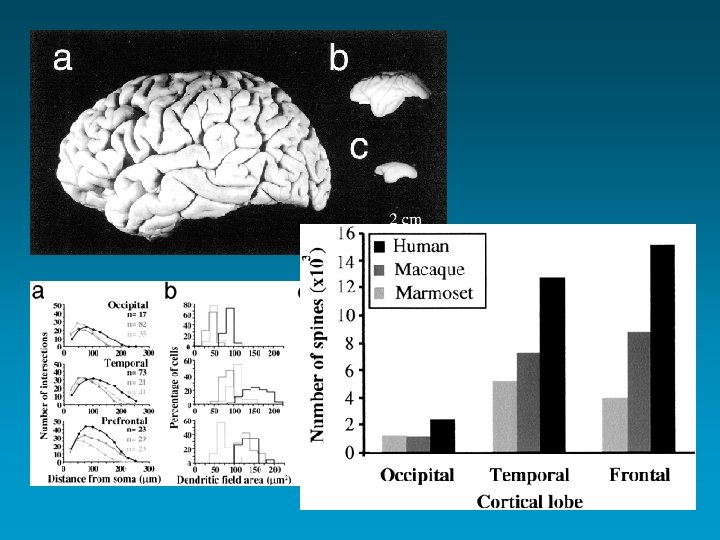
G Elston et al

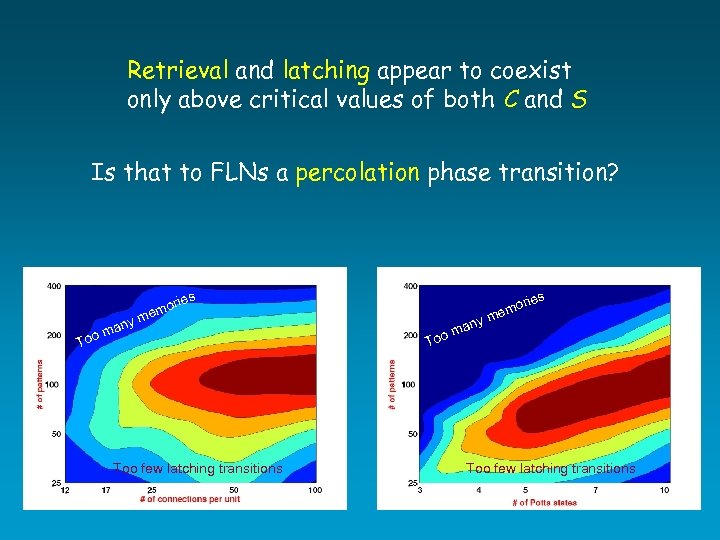
Retrieval and latching appear to coexist only above critical values of both C and S Is that to FLNs a percolation phase transition? s ny ma o m orie em To Too few latching transitions Too ny ma ries m o em Too few latching transitions

To go beyond statistics into syntax, a binding operation is required, with working memory differentiation implies multiple scaling relations “operators” r lf-o se d nize a g “fillers” pc C S 2 “fillers” input driven pl S ? nc ≈ √ 2 ________________ σ ln(p/√ 2π) (see Battaglia et al, Eliasmith et al, Fusi et al, Huyck, Hashimoto, . . )

Medium Term: to assess how any model can learn, one first needs a toy: (w/ E Kropff, a basic language including both syntax and A Grüning, M Katran semantics BLISS with mild guidance by G Longobardi) + semantic correlations Syntactic structure S DP I’ (singular/plural) I’ I VP I (singular or plural form) VP (Neg) (Adv. P) V’ V’ V DP | V S’ | V PP PP Prep DP S’ Compl S DP Det NP | Prop. N NP (Adj. P) N” N” (Adj. P) N’ N’ N (PP) | N S’ Det Art | Dem ? ≠ N boy | girl | cat | dog | tiger | jackal | horse | cow | meat | hay | milk | wood | meadow | stick | fork | bowl | cart | table | house || boys | girls | cats | dogs | tigers | jackals | horses | cows | stables | sticks | forks | bowls | carts | tables | houses Prop. N John | Mary || John and Mary V chases | feeds | sees | hears | walks | lives | eats | dies | kills | brings | pulls | is || chase | feed | see | hear | walk | live | eat | die | kill | bring | pull | are | Compl that | whether Prep in | with | to | of | under Neg does not || do not sing inflection of verb) (note singular negation removes Art the | a(an) Adj. P red | blue | green | black | brown | white | yellow | slow | fast | rotten | fresh | cold | warm | hot Adv. P slowly | rapidly | close | far Dem this | that || these | those

Hope for a simplified abstract formulation: G. Longobardi et al reduce 49 DP-internal parameters to just 4 parameter schemata:

the red paper sits with hot cats on the strong windows wonderful friends don't sit for a short kitchen the hot houses on cows don't find John teachers find a horse those rotten pens in the cow live in a meat the dogs don't wonder whether pens of the meat of that girl of the house w strong mothers give tables in that black meat to the red carts good boys hear Phoebe girls die for a strange dog kitchens with Mary give great husbands to the good houses these papers in mothers send the mother on the bed to the dogs in houses short dogs on farms of the hotels give Phoebe to the parents a cold lady with the women wonders whether Joe returns in a strange woman teachers of the man know whether these trees sit in the wonderful cat with the husbands come in friends girls with John find Joe uses a old fork of the great beds of the parents in the strange bed of c John wonders whether the parents on trees with the bowls don't give a cart strange wives run in tables John sends Mary to Phoebe men send the hot dog to the horse

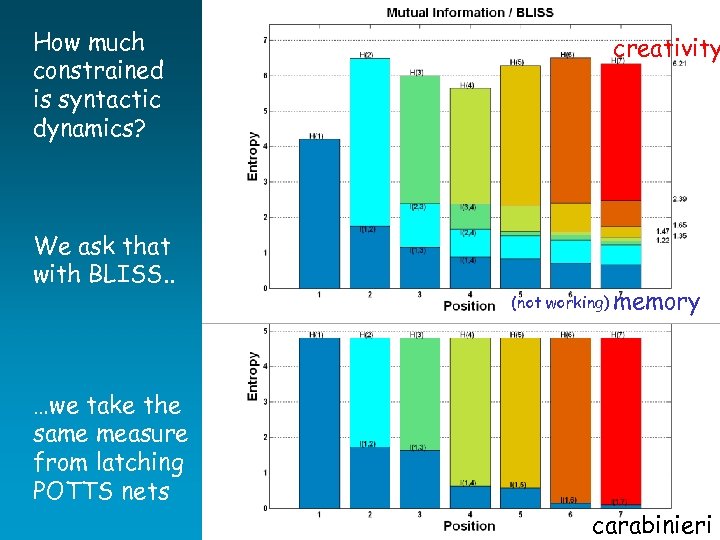
How much constrained is syntactic dynamics? We ask that with BLISS. . creativity (not working) memory …we take the same measure from latching POTTS nets carabinieri