Last time Basics of financial analysis

Last time…. • Basics of financial analysis • Estimating revenues and expenses is crucial • Time value of money concept • The significance of present value comparisons • Conversion of cash flows to present values

Profit Revisited • Profit = Revenues - Expenses • Expenses should include loss of value of equipment with time due to • Wear and Tear • Obsolescence • Loss of value (“expiration of assets”) is the basis of DEPRECIATION

Depreciation and Taxes • Suppose a company has $10 million in profits on December 31, i. e. Profits = Revenues - Expenses = $10, 000 • Corporate taxes are, in simplest terms, based on a a percentage of profits • Suppose that as a way of “beating taxes” the company purchases $10 million worth of new equipment on December 31 • Is the profit = 0?

No! Profit is not zero • The company has merely converted one asset (cash) to another (equipment). This is why Uncle Sam controls how equipment is “expensed”-- i. e. you cannot declare items of capital equipment as expenses when purchased. Instead, they are depreciated.

Depreciation Calculations. Information Needed We need: • Price originally paid for the equipment or asset • Estimate of lifetime (IRS) • Salvage Value at the end of lifetime • Calculations to be shown neglect special circumstances, e. g. investment tax credits, additional first year allowances

Depreciation • A new machine is not as good as an old machine • Depreciation is a way to account for the expiration of the machine, or any asset • Many methods: straight line versus accelerated • Has important tax consequences, which need to be considered in present value calculations

Mmmm…. Math Ci = Initial cost of an asset Cs = Final salvage value of an asset Cd =Depreciable cost =(Ci- Cs) m = lifetime for tax purposes (often differs from actual lifetime) dk = fractional depreciation in year k Dk = Dollar amount of depreciation, year k Dk = dk Cd , Book Value = Ci- Cd dk Book Value is often not true asset value.

Depreciation Methods • Straight Line Dk = Cd/m (same over lifetime) • Accelerated Depreciation – Double Declining Balance D 1 = Ci (2/m) B 1 = Ci - D 1 D 2 = B 1 (2/m) = [Ci (1 -2/m)](2/m)], etc. Link to Summary of Depreciation Methods

After-Tax Interest Rate • If we have an investment of $P yielding i interest per year, at the end of one year we have: P(1 + i) • We have to pay taxes on earnings Earnings = P(1 + i) - P = P i • Tax rate is T • Taxes = P i T • Real Earnings = Pi - P i T = Pi (1 - T) • Define after tax interest rate i. T = i(1 - T) • So, real after tax earnings = Pi. T • We will use i. T in after-tax comparisons

Consider the Effect of Depreciation and Taxes on Present Value (P) • If no depreciation & taxes, the decision to invest $Ci in a piece of equipment at time zero is worth P = -Ci • Reflects that Ci of cash of unavailable for other investments • Now, we need to consider the fact that depreciation gives us a tax savings each year

Cash Flow Time Line for Investments 0 D 1 T 1 D 2 T 2 D 3 T 3 D 4 T 4 • • • CS DNT N Ci • Cash outflow is shown below the line • Savings and/or revenues above the line • Cs is salvage value

Cash Flow Time Line for Investments 0 D 1 T 1 Ci = Ci D 2 T 2 D 3 T 3 D 4 T 4 • • • CS DNT N

After-Tax Cost Comparison Formulae Link to After-Tax Cost Comparison Formulae

Effect of Revenues in After Tax Comparisons • For every $R of revenue, a profit making firm pays $RT in tax where T = fractional tax rate • Thus, the firm actually keeps ($R - $RT) = $R(1 - T) • An after-tax cash flow time line would therefore have amounts as shown R(1 - T) 0 R(1 - T) 1 R(1 - T) 2 R(1 - T) 3 R(1 - T) 4 . . .

Expenses in After-Tax Comparisons • An expense of X in a particular tax year has two effects on cash flow -the actual out-of-pocket payment of X -the reduction of taxes as a result of the expense (XT) • Profit Before Expense (p) - Expense (X) = Profit After Expense (px) • Tax = px. T = p. T - XT • Profit after Taxes = px - px. T = px(1 - T) • Therefore, Effect of Expense = -X(1 - T)

After-Tax Cash Flow Time Line Showing Revenues, Expenses and Depreciation DT R(1 - T) 0 Ci 1 X(1 - T) DT DT CS DT R(1 - T) 2 3 X(1 - T) 4 X(1 - T) Note! Depreciation is not a real cash flow into company. It has the effect of reducing taxes. Note! No taxes associated with Ci or Cs terms.

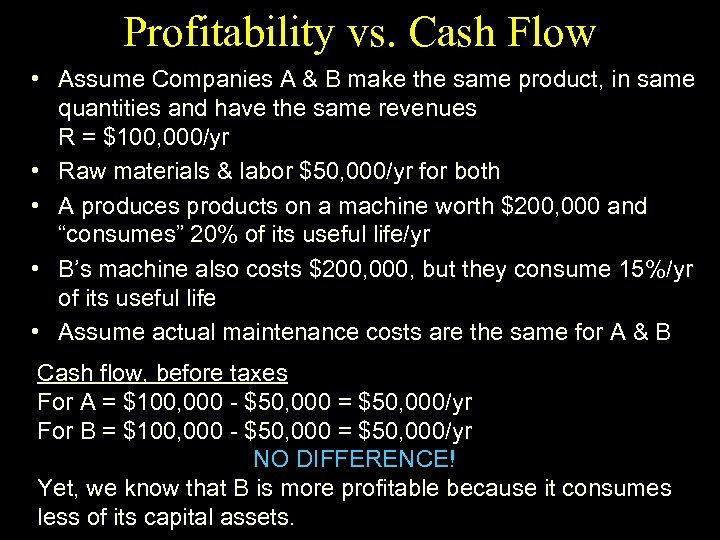
Profitability vs. Cash Flow • Assume Companies A & B make the same product, in same quantities and have the same revenues R = $100, 000/yr • Raw materials & labor $50, 000/yr for both • A produces products on a machine worth $200, 000 and “consumes” 20% of its useful life/yr • B’s machine also costs $200, 000, but they consume 15%/yr of its useful life • Assume actual maintenance costs are the same for A & B Cash flow, before taxes For A = $100, 000 - $50, 000 = $50, 000/yr For B = $100, 000 - $50, 000 = $50, 000/yr NO DIFFERENCE! Yet, we know that B is more profitable because it consumes less of its capital assets.

Profits (Including Depreciation) before Taxes • For A = $100, 000 - $50, 000 - (0. 20)(200, 000) = $10, 000/yr For B = $100, 000 - $50, 000 - (0. 15)(200, 000) = $20, 000/yr B shows itself to be better! • Taxes @ (50%) A = 0. 50($10, 000) = $5000 B = 0. 50($20, 000) = $10, 000 • After-Tax Income (Before Tax Profit) - (Taxes) A = 10, 000 - 5000 = $5000 B = 20, 000 - 10, 000 = $10, 000 • But after tax cash flow [R - X - Taxes] A = $100, 000 - $5000 = $45, 000 B = $100, 000 - $50, 000 - $10, 000 = $40, 000 Which company is better?

Which company is better? • B is the better company! • A has “turned” more of its assets into cash, but is using its assets less efficiently than B, as profit illustrates • Therefore, profitability = cash flow

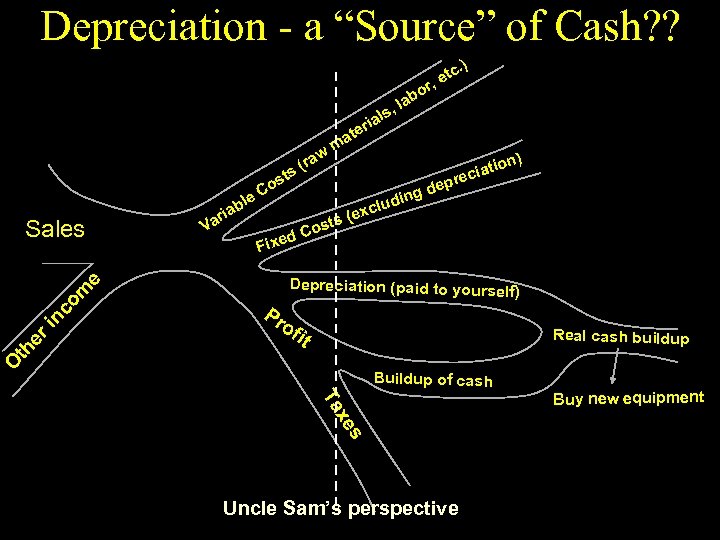
Depreciation - a “Source” of Cash? ? r, , ls ria w (ra s o lab te ma t le ts Cos ed om in c dep (e Depreciation (paid to yourself) Pr of it Real cash buildup O th er ng ludi xc ) tion a reci Fix e Sales Va b ria s Co ) tc. e Buildup of cash s xe Ta Uncle Sam’s perspective Buy new equipment

Profitability Measures Payout time / Payback period - Many definitions of this - Generally Payback Period (N, in years) = • Initial investment is Ci total investment for some people, only Cd (depreciable investment) for others • Income/yr for some is average profit/yr, excluding depreciation and taxes, but some include depreciation and taxes • Basic question addressed How soon do I recoup my original investment?

ROI (Return on Original Investment) ROI = • Neither payback period nor ROI explicitly considers the time value of money!

Preferred Methods • Net Present Value (NPV) Also known as Venture Worth (VW) • Discounted Cash Flow Rate of Return (DCFRR) Same as NPV = 0, solve for i. T • Iw = working capital (similar to initial investment in treatment)

Which Method is “Better”? • Net Present Value – Requires setting a value of i. T before you start – Any NPV > 0 means a worthwhile project – In choosing between alternatives with unequal lifetimes, need to choose on an annualized income basis (i. e. convert P X at end) • DCFRR – No need to have same time basis or to choose i. T a priori – Go down list from highest i. T to lowest (down to a minimum acceptable i. T)

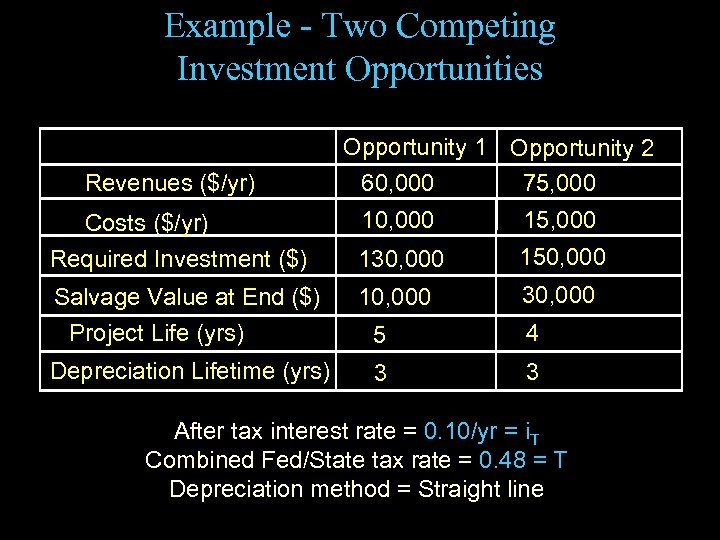
Example - Two Competing Investment Opportunities Revenues ($/yr) Costs ($/yr) Required Investment ($) Salvage Value at End ($) Project Life (yrs) Depreciation Lifetime (yrs) Opportunity 1 Opportunity 2 75, 000 60, 000 15, 000 130, 000 150, 000 10, 000 30, 000 5 4 3 3 After tax interest rate = 0. 10/yr = i. T Combined Fed/State tax rate = 0. 48 = T Depreciation method = Straight line

Cash Flow Time Lines (Amounts in 1000’s) • Opportunity 1 40 T 40 T 10 60(1 - T) 0 130 60(1 - T) 1 2 3 4 5 10(1 - T) 10(1 - T) Note: ND = depreciation lifetime = N = Project Lifetime

Cash Flow Time Lines (Amounts in 1000’s) • Opportunity 2 40 T 75(1 - T) 0 150 40 T 30 75(1 - T) 1 2 3 4 15(1 - T) Note: D =

Present Value Calculations

Present Value Calculations con’t • Since P 1 > 0 and P 2 > 0, do both projects, if possible • If can only choose one or the other • Choose Opportunity 1 over Opportunity 2 (X 1 > X 2) Note, if P 1 had been just a bit less, could have had P 1 > P 2 but X 1 < X 2. In this case, would choose Opportunity 2 instead. •

DCFRR • Let P 1 = 0 and solve for i. T • Need a root finding technique Know i. T > 0. 1 / yr • In this case (i. T)1 from (i. T)2 from • Choose projects based on i. T, highest to lowest until you run out of money to invest (Here, choose 1 over 2) • Use a graphical or numerical approach to solve for i. T

Continuous Interest and Discounting • Treats compounding in a continuous manner, as if in every infinitesimal time period, interest accrues (instead of only at year end): 1+ iannual = (1 + icont/k)k where there are k compounding periods per year. Now let k , (1 + icont/k)k e icont

Continuous Discounting Thus iannual = e icont -1 and S = P (1 + iannual )n = P (1 + e icont -1)n = P ein where it is now understood that in these types of calculations, i = icont Link to Continuous Interest Formulae