0251c27f5c2ea6ec21e4a5a45fc0107b.ppt
- Количество слайдов: 18
 Last lecture The electric dipole Electric field due to a dipole Electric dipole moment This lecture Continuous charge distributions Matter in electric fields
Last lecture The electric dipole Electric field due to a dipole Electric dipole moment This lecture Continuous charge distributions Matter in electric fields
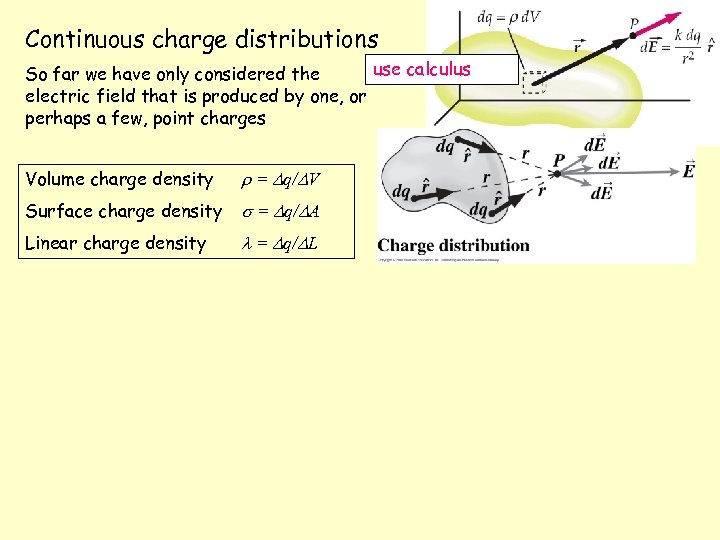 Continuous charge distributions use calculus So far we have only considered the electric field that is produced by one, or perhaps a few, point charges Volume charge density = q/ V Surface charge density = q/ A Linear charge density = q/ L
Continuous charge distributions use calculus So far we have only considered the electric field that is produced by one, or perhaps a few, point charges Volume charge density = q/ V Surface charge density = q/ A Linear charge density = q/ L
 Continuous charge distributions Here dq = d. V and the integration is over a volume. If the charge is distributed on a surface or a line, we use dq = d. A or dq = d. L Volume charge density = dq/d. V Surface charge density =dq/d. A Linear charge density = dq/d. L
Continuous charge distributions Here dq = d. V and the integration is over a volume. If the charge is distributed on a surface or a line, we use dq = d. A or dq = d. L Volume charge density = dq/d. V Surface charge density =dq/d. A Linear charge density = dq/d. L
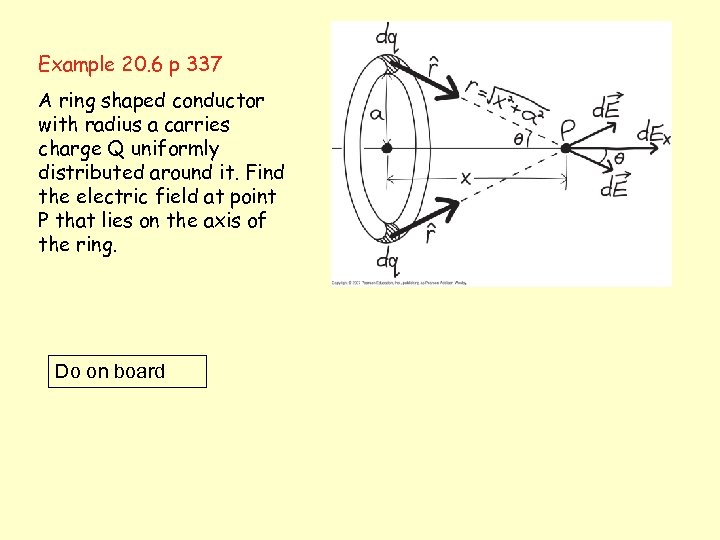 Example 20. 6 p 337 A ring shaped conductor with radius a carries charge Q uniformly distributed around it. Find the electric field at point P that lies on the axis of the ring. Do on board
Example 20. 6 p 337 A ring shaped conductor with radius a carries charge Q uniformly distributed around it. Find the electric field at point P that lies on the axis of the ring. Do on board
 Example 20. 7 p 337 Line Charge: a power line’s field A long, straight electric power line coincides with the x axis and carries a uniform line charge density λ (unit: C/m). Find the electric field on the y axis using the approximation that the wire is infinitely long. sinθ Please read through this example in the textbook. We will do a similar one in Wednesday’s workshop. θ
Example 20. 7 p 337 Line Charge: a power line’s field A long, straight electric power line coincides with the x axis and carries a uniform line charge density λ (unit: C/m). Find the electric field on the y axis using the approximation that the wire is infinitely long. sinθ Please read through this example in the textbook. We will do a similar one in Wednesday’s workshop. θ
 20. 5 Matter in electric fields To study the role of electric fields we need to separate two different tasks: 1) calculating the electric field produced by a given distribution of charge 2) calculating the force that a given field exerts on a charge placed in it. We have so far considered 1) with the electric field (from Coulomb’s Law) due to • • a point charge (done last lecture) Now we will consider 2) – what happens to an electric dipole charges placed in an a line of charge existing (external) a charged disk (in Wed Workshop) field.
20. 5 Matter in electric fields To study the role of electric fields we need to separate two different tasks: 1) calculating the electric field produced by a given distribution of charge 2) calculating the force that a given field exerts on a charge placed in it. We have so far considered 1) with the electric field (from Coulomb’s Law) due to • • a point charge (done last lecture) Now we will consider 2) – what happens to an electric dipole charges placed in an a line of charge existing (external) a charged disk (in Wed Workshop) field.
 20. 5 Matter in electric fields What happens to a charged particle when it is in an electric field produced by other stationary or slowly moving charges? An electrostatic force acts on the particle F=q. E in which q is the charge of the particle (including its sign) and E is the electric field that the other particles have produced at the position of the particle (an external field).
20. 5 Matter in electric fields What happens to a charged particle when it is in an electric field produced by other stationary or slowly moving charges? An electrostatic force acts on the particle F=q. E in which q is the charge of the particle (including its sign) and E is the electric field that the other particles have produced at the position of the particle (an external field).
 A positive charge that is free to move but is at rest in an electric field E will A. accelerate in the direction perpendicular to E B. remain at rest C. accelerate in the direction opposite to E D. accelerate in the same direction as E E. do none of the above Answer: D
A positive charge that is free to move but is at rest in an electric field E will A. accelerate in the direction perpendicular to E B. remain at rest C. accelerate in the direction opposite to E D. accelerate in the same direction as E E. do none of the above Answer: D
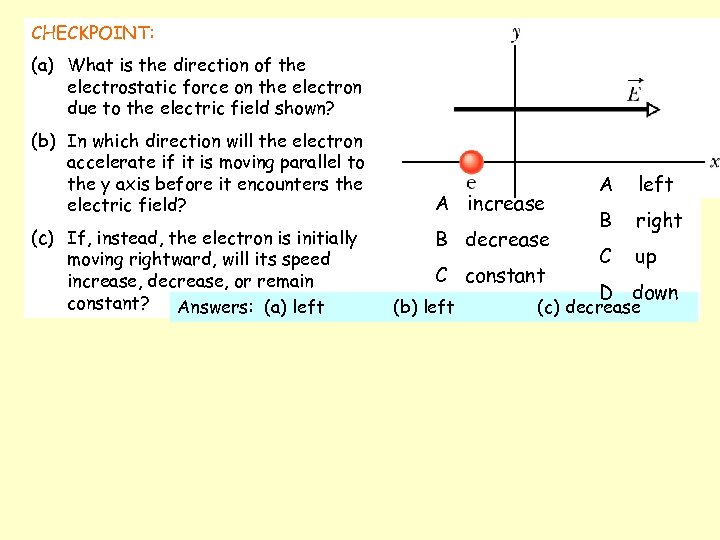 CHECKPOINT: (a) What is the direction of the electrostatic force on the electron due to the electric field shown? (b) In which direction will the electron accelerate if it is moving parallel to the y axis before it encounters the electric field? (c) If, instead, the electron is initially moving rightward, will its speed increase, decrease, or remain constant? Answers: (a) left A increase B decrease C constant (b) left A left B right C up D down (c) decrease
CHECKPOINT: (a) What is the direction of the electrostatic force on the electron due to the electric field shown? (b) In which direction will the electron accelerate if it is moving parallel to the y axis before it encounters the electric field? (c) If, instead, the electron is initially moving rightward, will its speed increase, decrease, or remain constant? Answers: (a) left A increase B decrease C constant (b) left A left B right C up D down (c) decrease
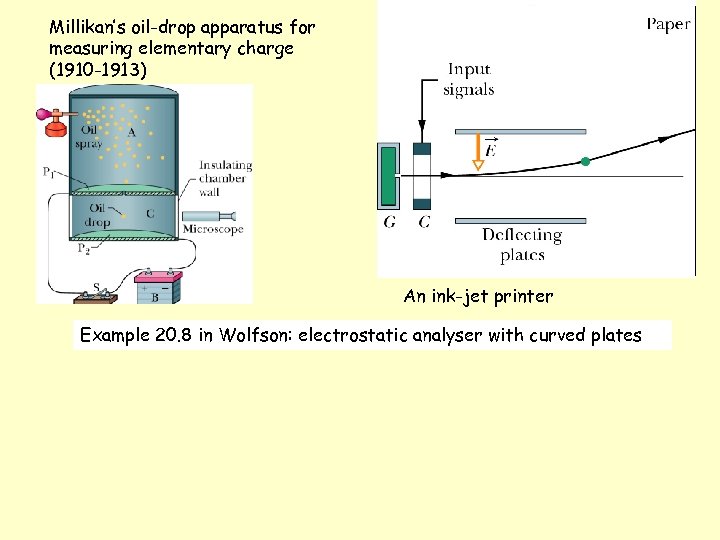 Millikan’s oil-drop apparatus for measuring elementary charge (1910 -1913) An ink-jet printer Example 20. 8 in Wolfson: electrostatic analyser with curved plates
Millikan’s oil-drop apparatus for measuring elementary charge (1910 -1913) An ink-jet printer Example 20. 8 in Wolfson: electrostatic analyser with curved plates
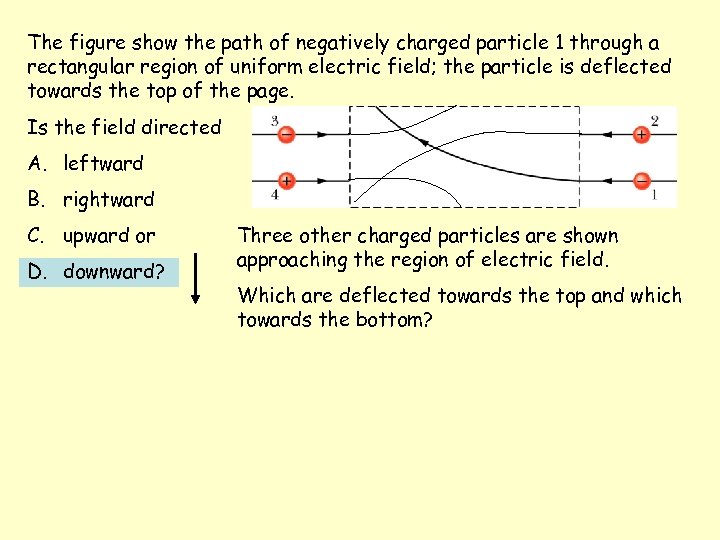 The figure show the path of negatively charged particle 1 through a rectangular region of uniform electric field; the particle is deflected towards the top of the page. Is the field directed A. leftward B. rightward C. upward or D. downward? Three other charged particles are shown approaching the region of electric field. Which are deflected towards the top and which towards the bottom?
The figure show the path of negatively charged particle 1 through a rectangular region of uniform electric field; the particle is deflected towards the top of the page. Is the field directed A. leftward B. rightward C. upward or D. downward? Three other charged particles are shown approaching the region of electric field. Which are deflected towards the top and which towards the bottom?
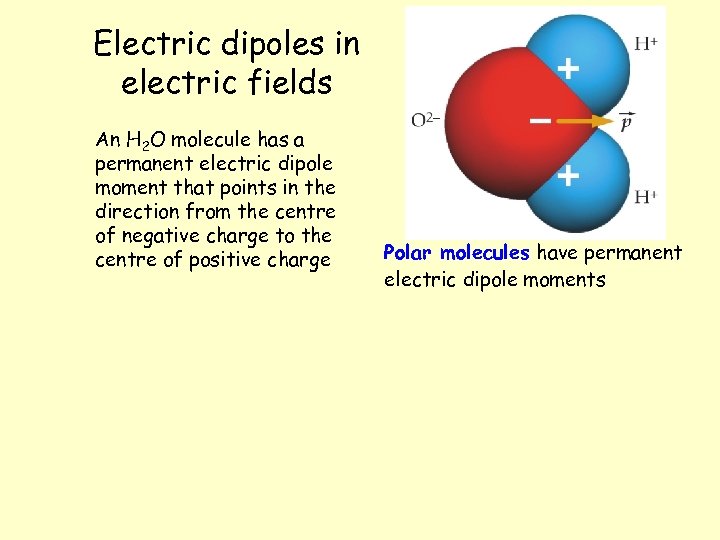 Electric dipoles in electric fields An H 2 O molecule has a permanent electric dipole moment that points in the direction from the centre of negative charge to the centre of positive charge Polar molecules have permanent electric dipole moments
Electric dipoles in electric fields An H 2 O molecule has a permanent electric dipole moment that points in the direction from the centre of negative charge to the centre of positive charge Polar molecules have permanent electric dipole moments
 A dipole in a uniform electric field experiences equal and opposite forces that tend to rotate the dipole so that its dipole moment is aligned with the electric field (torque). Field E causes a torque on the dipole. The direction of the torque is into the page, which we show by the symbol . This defines the direction of rotation. = p x E See more on torques in Wolfson 10. 2, p 158
A dipole in a uniform electric field experiences equal and opposite forces that tend to rotate the dipole so that its dipole moment is aligned with the electric field (torque). Field E causes a torque on the dipole. The direction of the torque is into the page, which we show by the symbol . This defines the direction of rotation. = p x E See more on torques in Wolfson 10. 2, p 158
 Nonpolar molecules have no permanent dipole moment. In an external electric field, E, the charges within the molecule become separated in space……it acquires an induced dipole moment parallel to E. It is said to be polarised.
Nonpolar molecules have no permanent dipole moment. In an external electric field, E, the charges within the molecule become separated in space……it acquires an induced dipole moment parallel to E. It is said to be polarised.
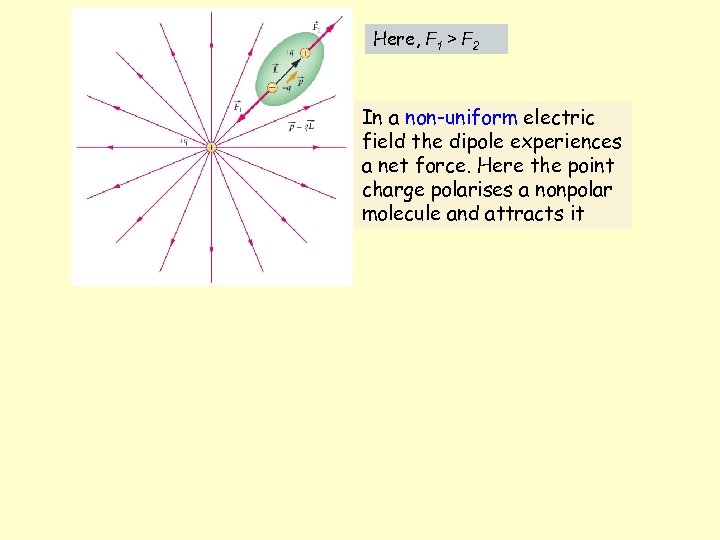 Here, F 1 > F 2 In a non-uniform electric field the dipole experiences a net force. Here the point charge polarises a nonpolar molecule and attracts it
Here, F 1 > F 2 In a non-uniform electric field the dipole experiences a net force. Here the point charge polarises a nonpolar molecule and attracts it
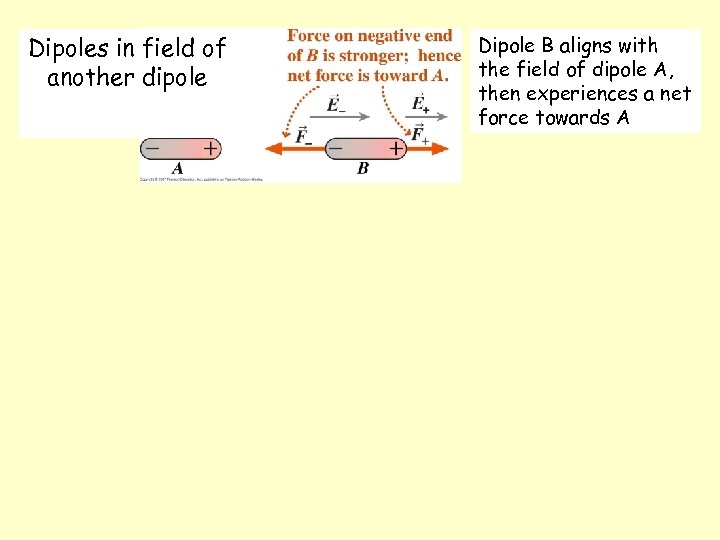 Dipoles in field of another dipole Dipole B aligns with the field of dipole A, then experiences a net force towards A
Dipoles in field of another dipole Dipole B aligns with the field of dipole A, then experiences a net force towards A
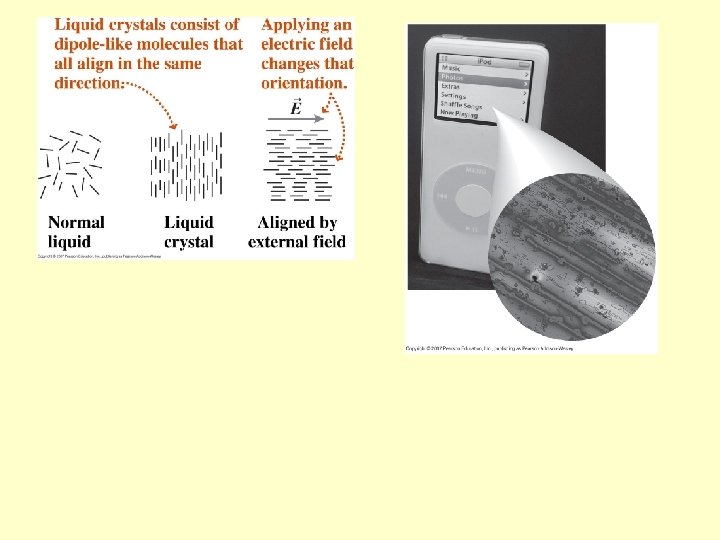
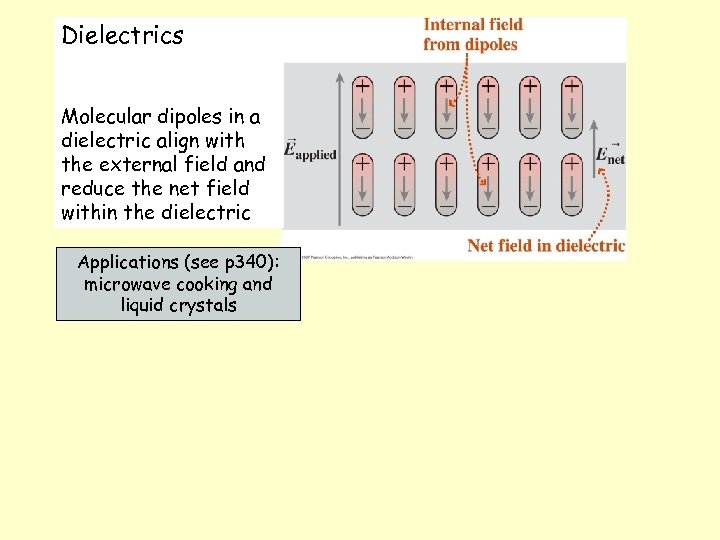 Dielectrics Molecular dipoles in a dielectric align with the external field and reduce the net field within the dielectric Applications (see p 340): microwave cooking and liquid crystals
Dielectrics Molecular dipoles in a dielectric align with the external field and reduce the net field within the dielectric Applications (see p 340): microwave cooking and liquid crystals