Laser Induced Control of Condensed Phase Electron Transfer Rob

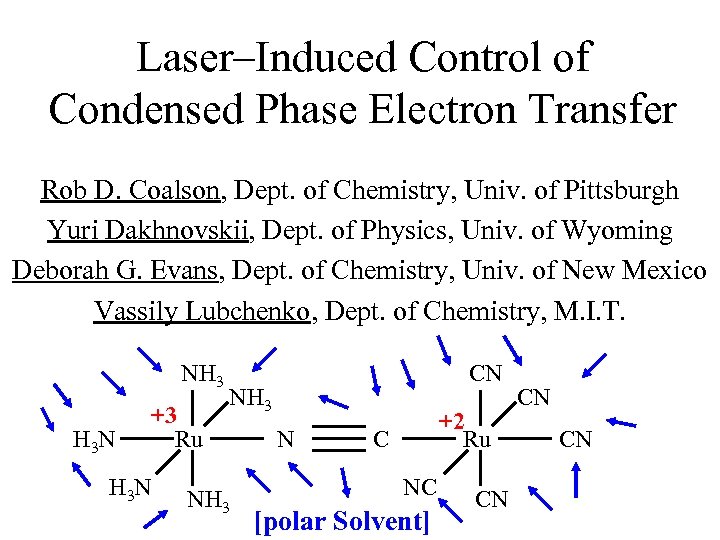
Laser–Induced Control of Condensed Phase Electron Transfer Rob D. Coalson, Dept. of Chemistry, Univ. of Pittsburgh Yuri Dakhnovskii, Dept. of Physics, Univ. of Wyoming Deborah G. Evans, Dept. of Chemistry, Univ. of New Mexico Vassily Lubchenko, Dept. of Chemistry, M. I. T. NH 3 H 3 N +3 Ru H 3 N CN NH 3 N +2 Ru C NC [polar Solvent] CN CN CN

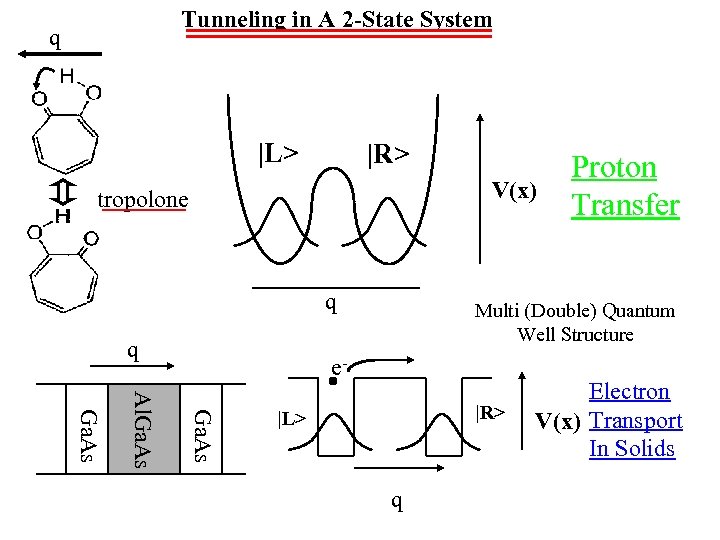
Tunneling in A 2 -State System q |L> |R> V(x) tropolone q q Proton Transfer Multi (Double) Quantum Well Structure e. Ga. As Al. Ga. As |R> |L> q Electron V(x) Transport In Solids

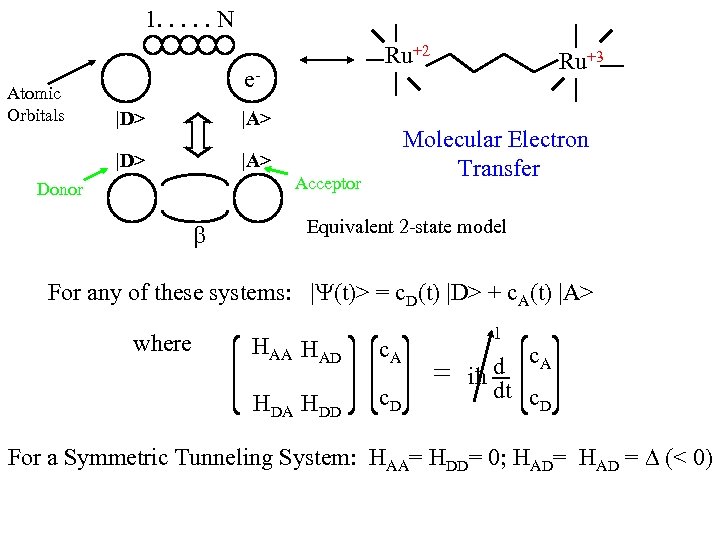
1. . . N Atomic Orbitals Ru+2 e|D> |A> Molecular Electron Transfer Acceptor Donor Ru+3 Equivalent 2 -state model For any of these systems: | (t)> = c. D(t) |D> + c. A(t) |A> where HAA HAD c. A HDD c. D 1 = d c. A iħ dt c D For a Symmetric Tunneling System: HAA= HDD= 0; HAD= HAD = (< 0)

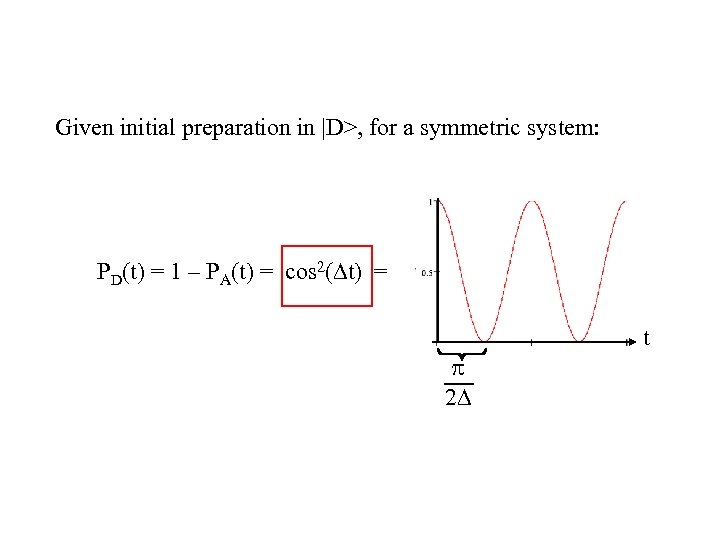
Given initial preparation in |D>, for a symmetric system: PD(t) = 1 – PA(t) = cos 2( t) = t 2

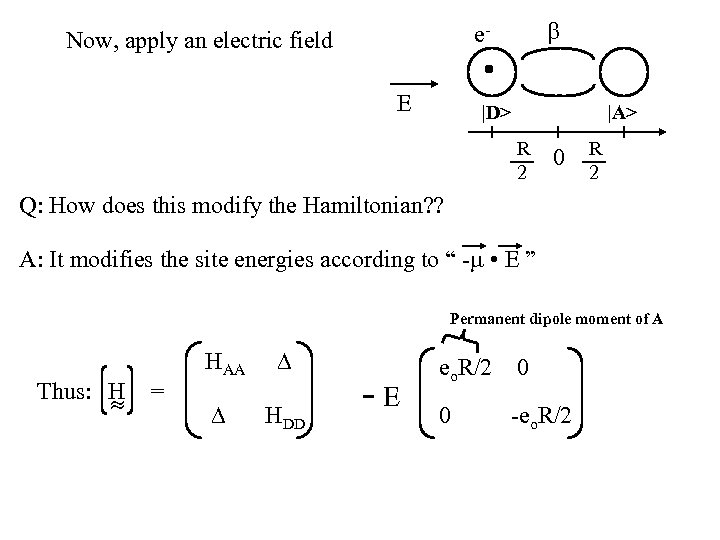
e- Now, apply an electric field E |D> |A> R 2 0 R 2 Q: How does this modify the Hamiltonian? ? A: It modifies the site energies according to “ - • E ” Permanent dipole moment of A Thus: H = HAA HDD -E eo. R/2 0 0 -eo. R/2

Analysis in the case of time-dependent E(t) = Eocos ot Consider first the symmetric case: i d c. A dt c. D 0 = 0 1 o o c. A 0 -1 - E cos t 0 c. D Permanent dipole moment difference Letting: c. A(t) = e i a sin ot c. AI(t) ; c. D(t) = e i a sin ot c. DI(t) Eo Where: a = (ħ) o t [ N. B. : E cos t'dt' = 0 o o Eo sin ot ] o Thus, Interaction Picture S. E. reads: I d c. A i = dt I c. D 0 e 2 i a sin ot e-2 i a sin ot 0 c AI c DI

Now note: So: e i b sin t = m=- Jm(b) e i m t e 2 i a sin ot = m=- Jm(2 a) e i m ot ·Jo(2 a) , for / o << 1 RWA Thus, the shuttle frequency is renormalized to |Jo(2 a)| NB: Trapping or localization occurs at certain Eo values! 0 [ 0 2. 5 <<1 ] 5. 5 a [Grossman - Hänggi, Dakhnovskii – Metiu]

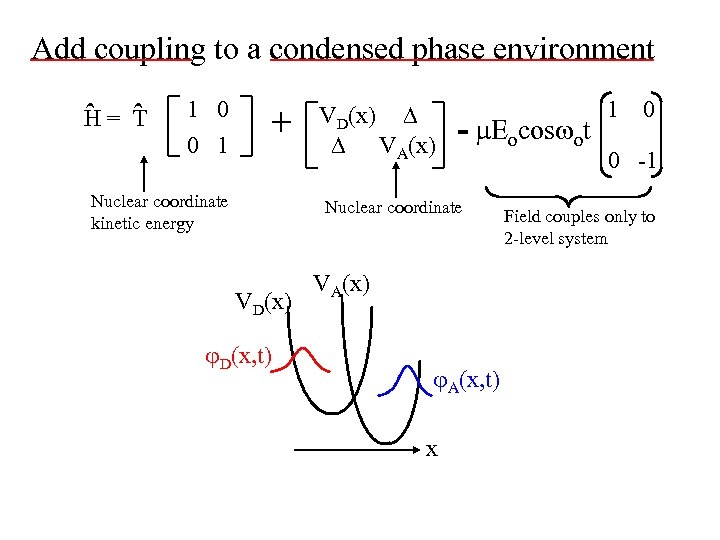
Add coupling to a condensed phase environment ˆ ˆ H= T 1 0 0 1 + Nuclear coordinate kinetic energy VD(x) VA(x) - Eocos ot Nuclear coordinate VD(x) D(x, t) VA(x) A(x, t) x 1 0 0 -1 Field couples only to 2 -level system

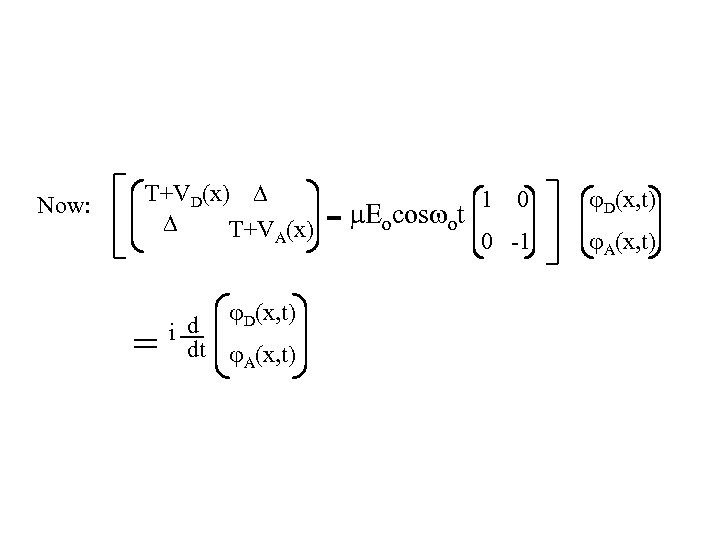
Now: T+VD(x) T+VA(x) = D(x, t) d i dt A(x, t) - E cos t 0 1 o o 0 D(x, t) -1 A(x, t)

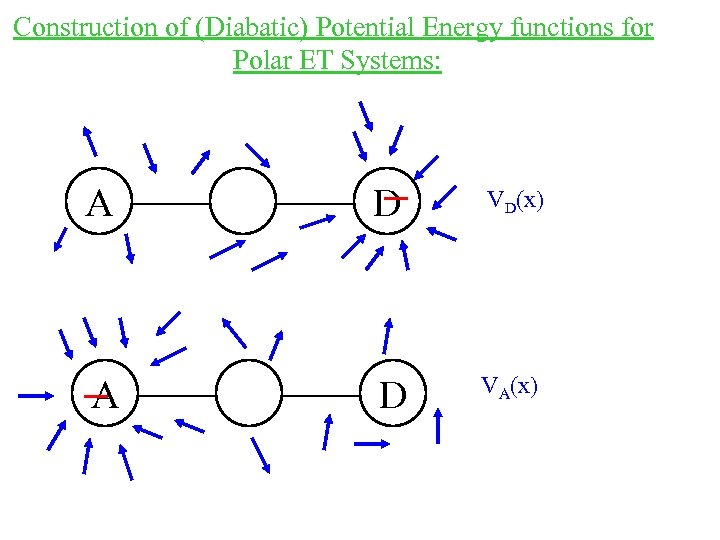
Construction of (Diabatic) Potential Energy functions for Polar ET Systems: A D VD(x) A D VA(x)

A few features of classical Nonadiabatic ET Theory [Marcus, Levich-Doganadze…] ˆ H = ˆ 1(x) T+V non-adiabatic coupling matrix element ˆ 2(x) T+V Hamiltonian kinetic E of nuclear coordinates | (t)> = 1(x, t) 2(x, t) (diabatic) nuclear coord. potential for electronic state 2 States

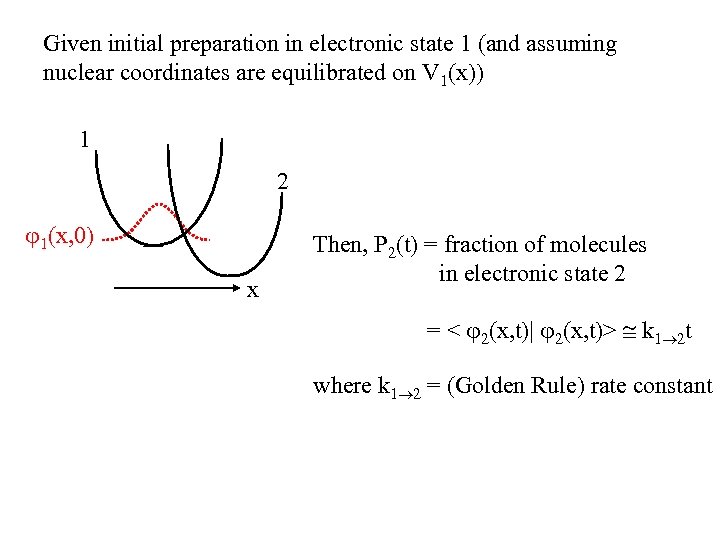
Given initial preparation in electronic state 1 (and assuming nuclear coordinates are equilibrated on V 1(x)) 1 2 1(x, 0) x Then, P 2(t) = fraction of molecules in electronic state 2 = < 2(x, t)| 2(x, t)> k 1 2 t where k 1 2 = (Golden Rule) rate constant

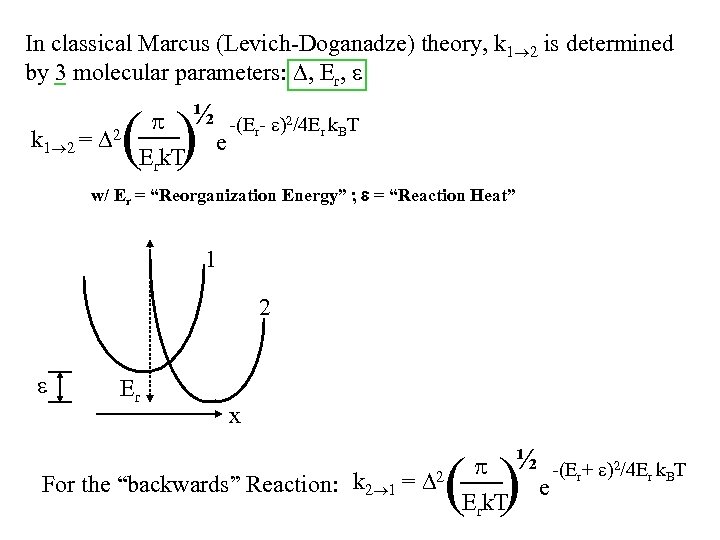
In classical Marcus (Levich-Doganadze) theory, k 1 2 is determined by 3 molecular parameters: , Er, k 1 2 = 2 ½ -(Er- )2/4 Er k. BT e Erk. T ( ) w/ Er = “Reorganization Energy” ; = “Reaction Heat” 1 2 Er x ½ -(Er+ )2/4 Er k. BT e Erk. T ( ) For the “backwards” Reaction: k 2 1 = 2

To obtain electronic state populations at arbitrary times, solve kinetic [“Master”] Eqns. : d. P 1(t)/dt = - k 1 2 P 1(t) + k 2 1 P 2(t) d. P 2(t)/dt = k 1 2 P 1(t) - k 2 1 P 2(t) Note that long-time asymptotic [“Equilibrium”] distributions are then given by: Keq P 2( ) k 1 2 = = P 1( ) k 2 1 = e /k. BT for Marcus formula rate constants N. B. Marcus theory for nonadiabatic ET reactions works experimentally. See: Closs & Miller, Science 240, 440 (1988)

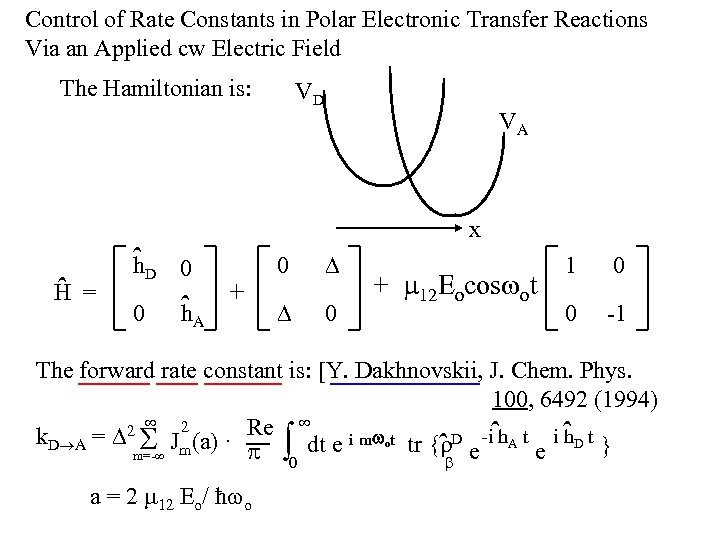
Control of Rate Constants in Polar Electronic Transfer Reactions Via an Applied cw Electric Field The Hamiltonian is: ˆ H = VD VA x ˆD h 0 0 ˆA h + 0 0 + 12 Eocos ot 1 0 0 -1 The forward rate constant is: [Y. Dakhnovskii, J. Chem. Phys. 100, 6492 (1994) 2 Re 2 h k. D A = Jm(a) · dt e i m ot tr { D e -iˆh. A t e i ˆ D t } ˆ 0 m=- a = 2 12 Eo/ ħ o

2 k. D A = 4 A D ½ Erk. T ( ) m=- 2 Jm(2 12 Eo/ħ o) • e + -(Er – + ħm o)2/4 Er k. BT Rate constants in presence of cw E-field

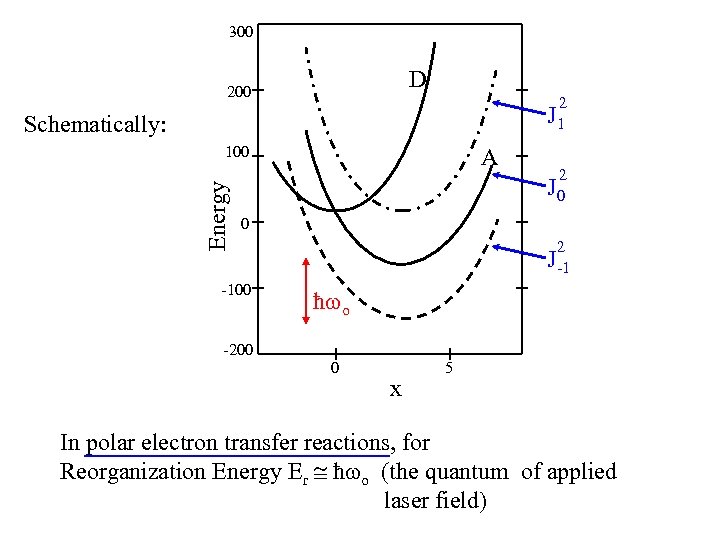
300 D 200 2 J 1 Schematically: Energy 100 A 2 J 0 0 -100 2 J-1 ħ o -200 0 x 5 In polar electron transfer reactions, for Reorganization Energy Er ħ o (the quantum of applied laser field)

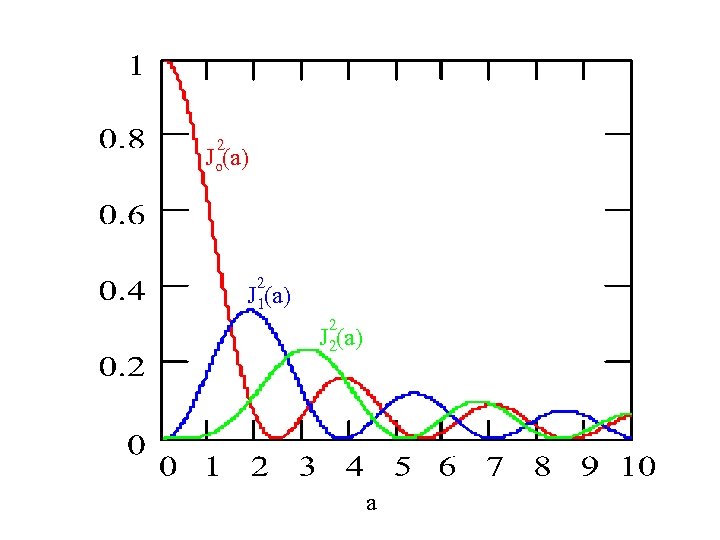
2 Jo(a) 2 J 1(a) 2 J 2(a) a

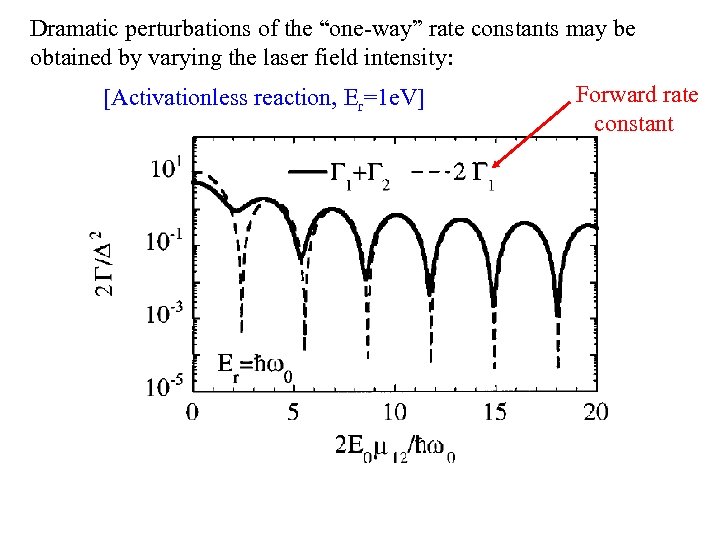
Dramatic perturbations of the “one-way” rate constants may be obtained by varying the laser field intensity: [Activationless reaction, Er=1 e. V] Forward rate constant

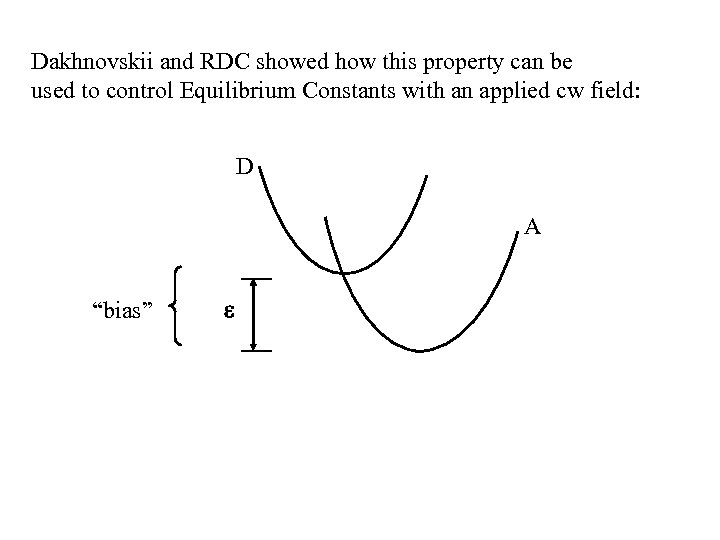
Dakhnovskii and RDC showed how this property can be used to control Equilibrium Constants with an applied cw field: D A “bias”

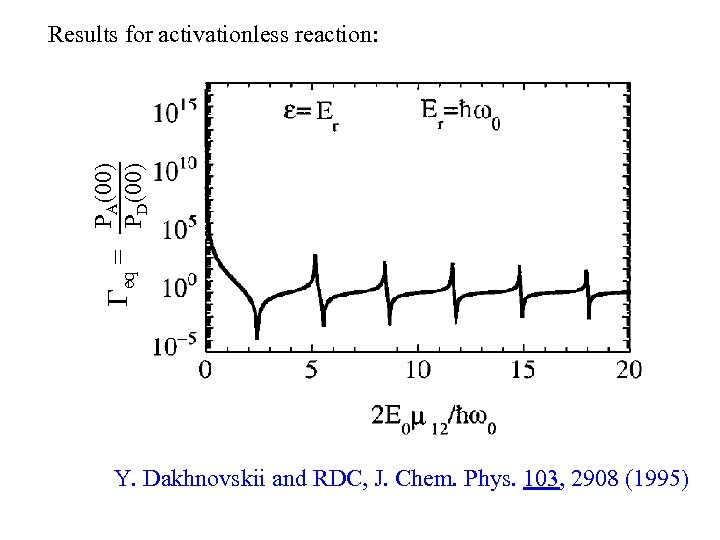
PA(00) eq = PD(00) Results for activationless reaction: Y. Dakhnovskii and RDC, J. Chem. Phys. 103, 2908 (1995)

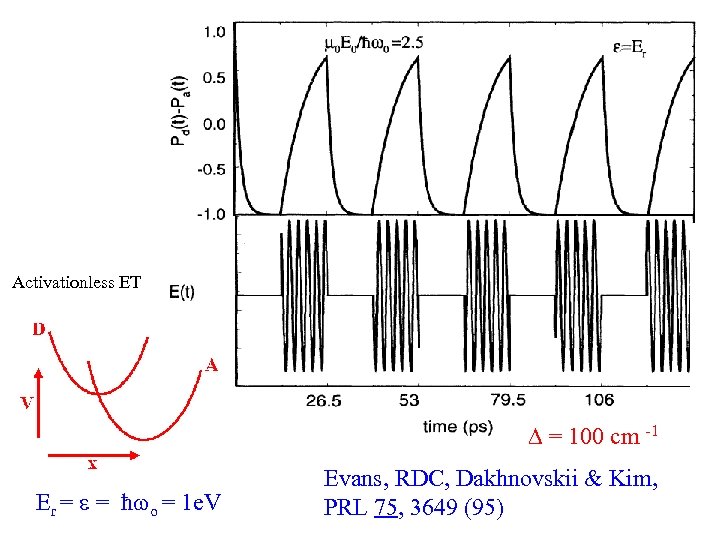
Activationless ET = 100 cm -1 Er = = ħ o = 1 e. V Evans, RDC, Dakhnovskii & Kim, PRL 75, 3649 (95)

REALITY CHECK on coherent control of mixed valence ET reactions in polar media (1) “ ·E” E Orientational averaging will reduce magnitude of desired effects [Lock ET system in place w/ thin polymer films]

(2) Dielectric breakdown of medium? To achieve resonance effects for = 34 D Er = ħ o = 1 e. V Electric field 107 V/cm Giant dipole ET complex, solvent w/ reduced Er, pulsed laser reduce likelihood of catastrophe] (3) Direct coupling of E(t) to polar solvent [Dipole moment of solvent molecules << Dipole moment of giant ET complex]

(4) ħ 0 1 e. V ; intense fields (multiphoton) excitation to higher energy states in the ET molecule, which are not considered in the present 2 -state model. ħ 1 e. V

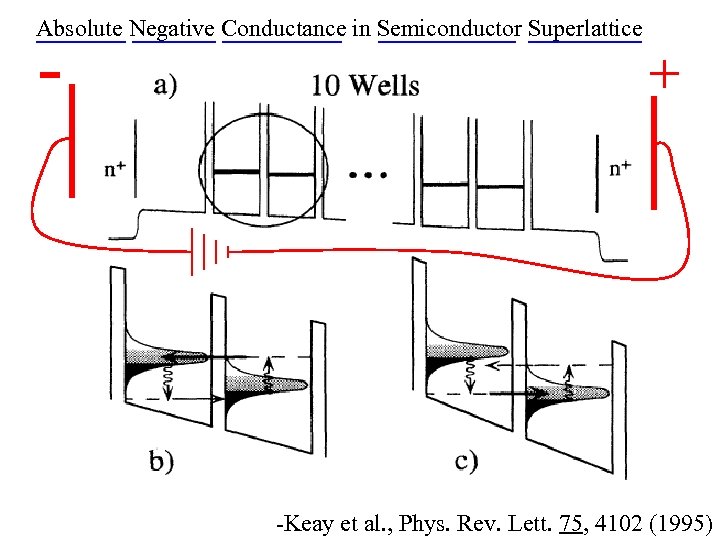
Absolute Negative Conductance in Semiconductor Superlattice - + -Keay et al. , Phys. Rev. Lett. 75, 4102 (1995)

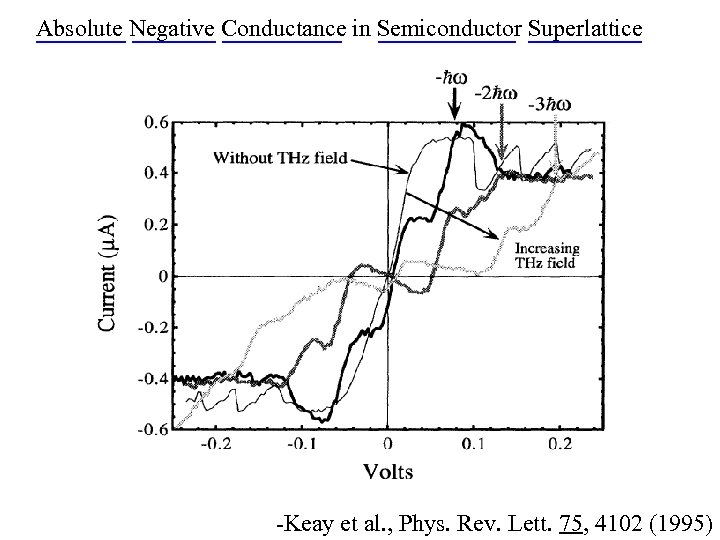
Absolute Negative Conductance in Semiconductor Superlattice -Keay et al. , Phys. Rev. Lett. 75, 4102 (1995)

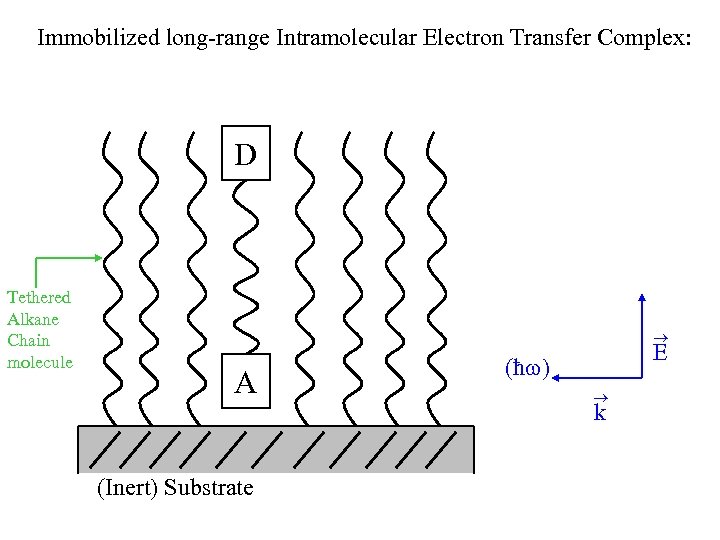
Immobilized long-range Intramolecular Electron Transfer Complex: D Tethered Alkane Chain molecule A (Inert) Substrate E (ħ ) k

ħ ħ Light Absorption by Mixed Valence ET Complexes in Polar Solvents: Ru+3 Ru+2 ħ ħ Incident Photons Solvent Transmitted Photons

Absorption Cross Section Formula:

Marcus Gaussian Δ permanent dipole moment difference

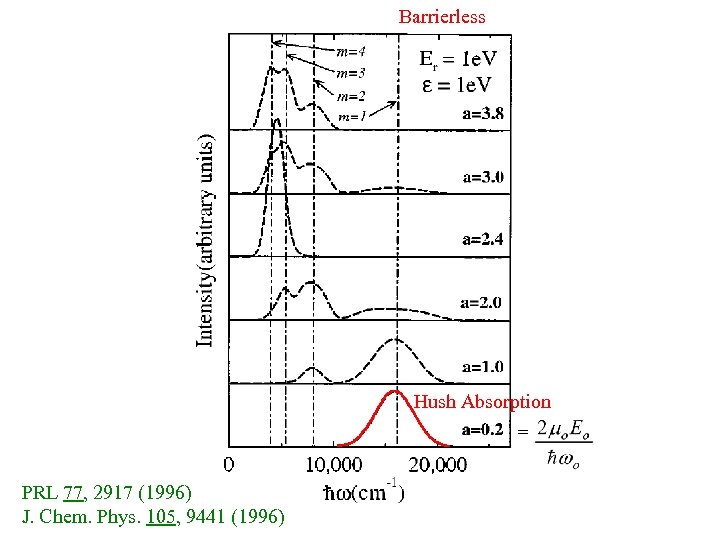
Barrierless Hush Absorption = PRL 77, 2917 (1996) J. Chem. Phys. 105, 9441 (1996)

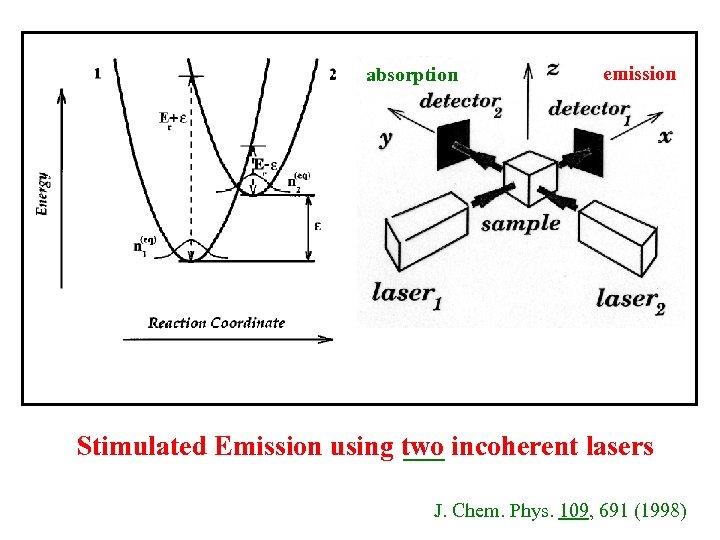
absorption emission Stimulated Emission using two incoherent lasers J. Chem. Phys. 109, 691 (1998)

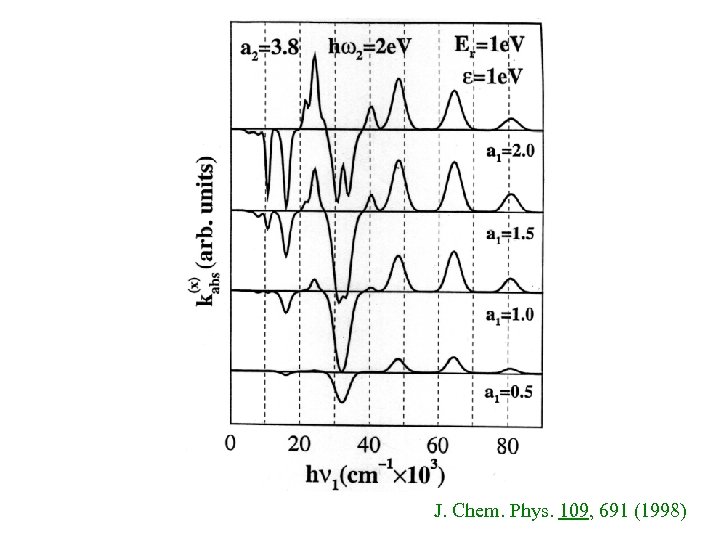
J. Chem. Phys. 109, 691 (1998)