Land Use in Monocentric City Chapter 8 O Sullivan

Land Use in Monocentric City Chapter 8 O’Sullivan

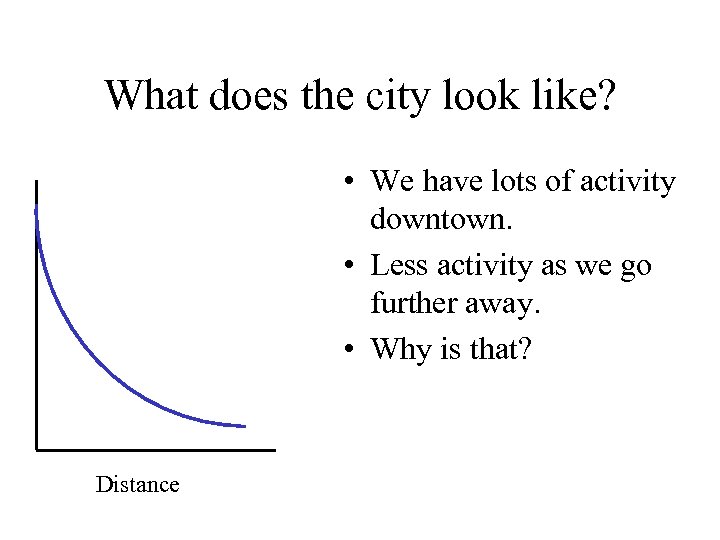What does the city look like? • We have lots of activity downtown. • Less activity as we go further away. • Why is that? Distance

Answers • Transportation technologies lead to nodes from which we ship items. • Scale economies imply that we are likely to see clustering around activities that are subject to economies of scale. • There are informational and shopping externalities.

Who locates where? • The fundamental story is one that we’ve seen before. • Firms maximize profits. The profits come from a function that looks like this: • = Rev - Costs - transportation costs - rent • If there is perfect competition, = 0. • So:

Who locates where? • 0 = Rev - Costs - transportation costs - rent • rent = Rev. - Costs - t. Xu – where X is what is shipped, t is the cost per unit to ship it, and u is the distance shipped. • So: – Rent is inversely related to distance.

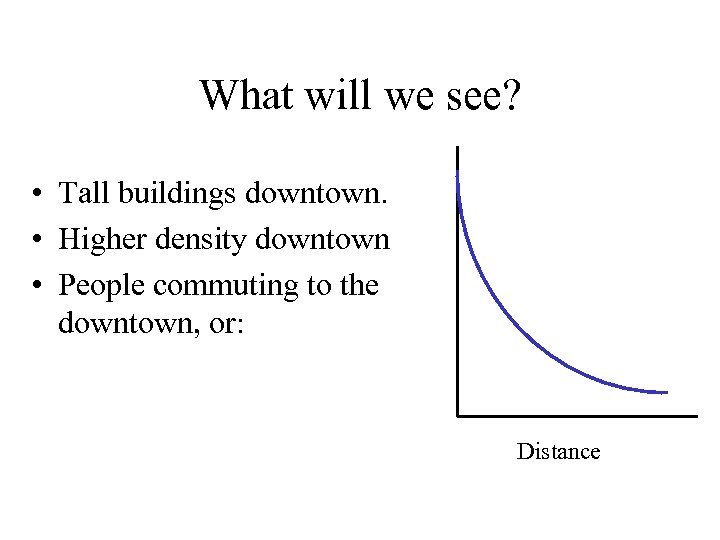What will we see? • Tall buildings downtown. • Higher density downtown • People commuting to the downtown, or: Distance

Is this efficient? • What is efficient? Answer -- Since production is usually taken as fixed, the efficient allocation minimizes transportation costs. Those with the highest transportation costs are locating the closest, so the allocation is efficient.

What about households? • Households don’t maximize profits, so let’s look, first, at their budgets, but then look at their utility. • Households, in this model, eat chicken, rent housing, and commute to work. So: • Income = Chick. Exp. + House Exp. + trav. • y = 1 * c + p * h + tu

Household expenditures • y = 1 * c + p * h + tu – where c = pounds of chicken at $1/pound – h = housing, at price p – u = distance commuting at price t/mile • As the household moves further away from downtown, what MUST change? A> Commuting cost . Then what?

Household expenditures Then what? • Does the price of chicken change? • OK, transportation costs go up by $t. So, the price of housing must fall in order to make up for the transportation costs. • If tu increases, ph must decrease, or else income rises.

Household expenditures • So if we move 1 mile further, transportation cost increases by $t. Thus: • t = - h p, or: • p = -t / h. • Let’s look at a spreadsheet (EXCEL).

What does this say about the rents? • p = -t / h. • This is a straight line, just like we saw before. • What kinds of substitutions might we see? • A picture!

Indifference curves • Suppose Clyde takes home $2, 000 per month. Clyde lives on chicken and housing, and commutes to work. • Chicken costs $1/pound. • Housing costs $0. 50/sq. ft. • Commuting costs $100. • All are per month.

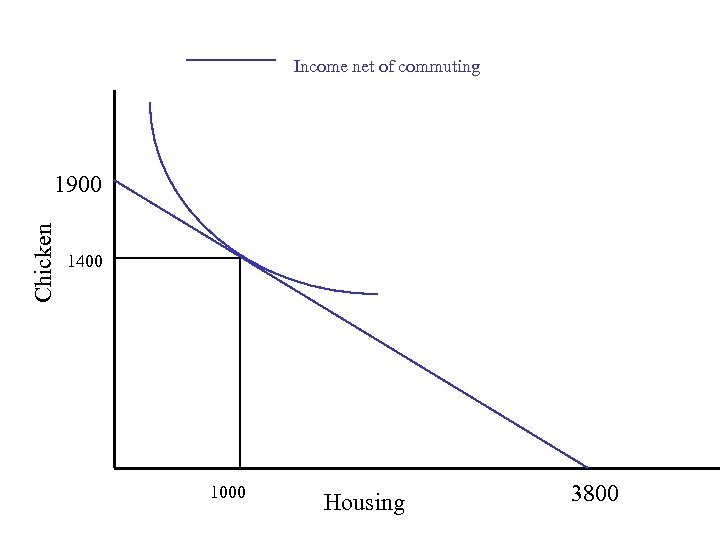Income net of commuting Chicken 1900 1400 1000 Housing 3800

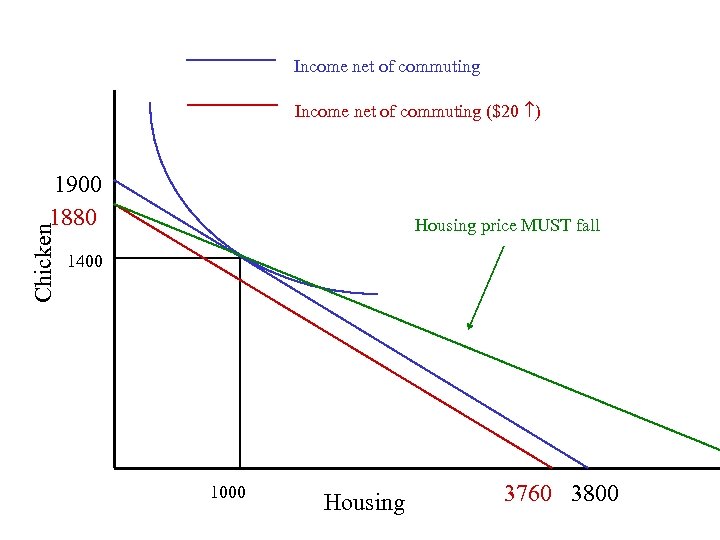Income net of commuting ($20 ) Chicken 1900 1880 Housing price MUST fall 1400 1000 Housing 3760 3800

Housing price falls • People must stay on same indifference curve! • As price of housing falls, people substitute away from chicken. Utility rises. • To keep utility the same, price of housing is bid up a little more than the transportation costs would indicate. This makes it convex.

Rich and poor • Let’s compare the rich and the poor. • Look at the equation: • p = -t / h. What changes between the rich and the poor? A> The rich buy more h than the poor. So, the denominator of the equation is bigger. The price of housing must fall LESS per square foot per mile for the rich than for the poor.

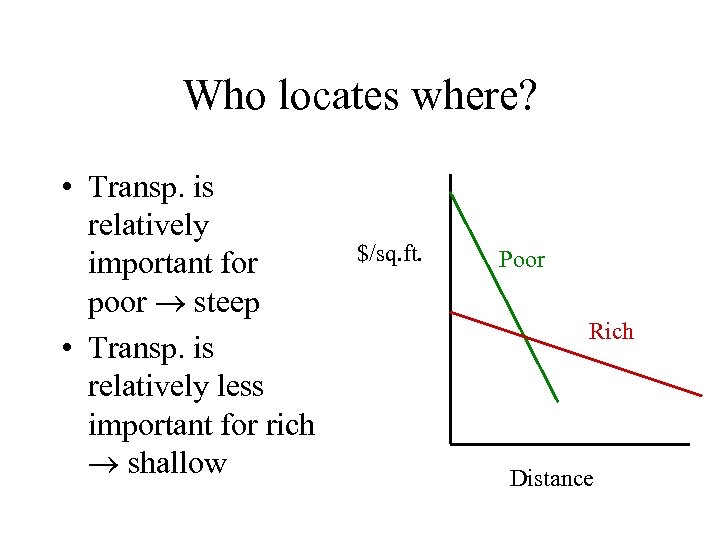Who locates where? • Transp. is relatively important for poor steep • Transp. is relatively less important for rich shallow $/sq. ft. Poor Rich Distance

Who locates where? • Poor in central city, rich further out. Why? • Look at EXCEL spreadsheet and discuss. • Next time: – Density – Segregation