7.ppt
- Количество слайдов: 11

ЛАБОРАТОРНАЯ РАБОТА № 7 Тема: Решение граничных задач для обыкновенных дифференциальных уравнений

1. ПОСТАНОВКА ЗАДАЧИ В граничных задачах для обыкновенных дифференциальных уравнений дополнительные условия, присоединяемые к дифференциальным уравнениям, задаются в виде уравнений, содержащих комбинации значений решения и его производных, взятых в нескольких точках отрезка, на котором разыскивается решение. Пусть дано уравнение (1) Двухточечная граничная задача для уравнения (1) ставится следующим образом: найти функцию , которая на отрезке удовлетворяет (1), а на концах отрезка – граничным условиям: (2) (3) 2

Если уравнения (1) – (3) линейные относительно то граничная задача (1) – (3) называется линейной. Для простоты ограничимся случаем линейной граничной задачи при. Тогда дифференциальное уравнение и условия записываются в виде , (4) (5) (6) где известные функции; заданные постоянные. Будем предполагать, что существует, единственна и существуют производные от достаточно высокого порядка. Для этого необходимо выполнение условий. 3

2. МЕТОД СЕТОК РЕШЕНИЯ ГРАНИЧНЫХ ЗАДАЧ ДЛЯ ОБЫКНОВЕННЫХ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ Рассмотрим метод сеток на примере простейших граничных задач для дифференциальных уравнений второго порядка (4) – (6). 1. На отрезке выбирается конечное множество точек Совокупность этих точек называют сеткой, каждую из точек узлом сетки. Если сетка равномерная, то (7) 2. Граничная задача (4) – (6) заменяется системой алгебраических уравнений, неизвестными в которых являются величины, «близкие» к решению граничной задачи в точках. 3. Система алгебраических уравнений решается по какому-либо численному алгоритму и тем самым находится приближенное решение граничной задачи. 4

Для построения системы алгебраических уравнений можно использовать замену производных через значения функции. Замена может быть получена различными способами. Например, воспользовавшись разложением в ряд Тейлора, в случае сетки (7) можно записать: (8) (9) (10) (11) Предполагаем, что имеет непрерывные производные до четвертого порядка включительно. Используя (8) – (11), из уравнений (4), (5) и (6) получаем систему (12)– (14). 5

3. МЕТОД ПРОГОНКИ Система линейных алгебраических уравнений, аппроксимирующая граничную задачу (4)–(6) для линейных дифференциальных уравнений второго порядка, имеет вид: где (12) (13) (14) – некоторые числа. Решение системы (12) – (14) по методу правой прогонки состоит в следующем: 1) находим значения 2) по рекуррентным формулам последовательно вычисляем 3) находим 4) по формуле вычисляем . 6

Первые два этапа называют прямой прогонкой, два последующие – обратной прогонкой. Они выполнены при условии, что. Метод правой прогонки будет устойчив к погрешностям округления при выполнении условий: (15) При выполнении этих условий погрешность решения системы (12) – (14) по описанному алгоритму может быть значительной. Если выполняются условия: (16) можно применить метод левой прогонки, который в этом случае будет устойчив к погрешностям округлений. Он состоит в следующем: 1) находим значения 2) по рекуррентным формулам вычисляем 7

3) находим 4) по рекуррентным соотношениям определяем . Отметим, что при выполнении ограничений (15) и (16) будут выполняться условия: или Условия или в этом случае будут выполняться, если система (12) – (14) имеет единственное решение. 8

Пример. Найти решение граничной задачи в точках по методу сеток. Решение. Граничная задача аппроксимируется на сетке разностной схемой: , Для решения полученной системы будем использовать метод правой прогонки. Вначале находим прогоночные коэффициенты по соотношениям После этого значения вычисляем по соотношениям: 9
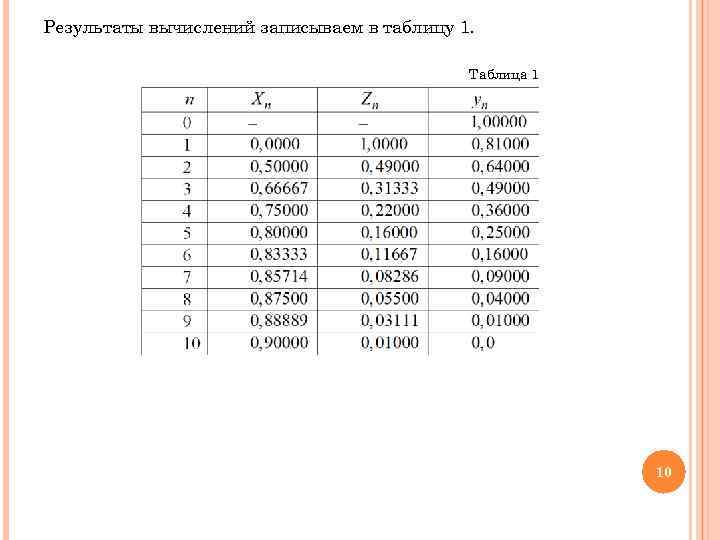
Результаты вычислений записываем в таблицу 1. Таблица 1 10

ЗАДАНИЕ № 7 Тема: Решение дифференциальных уравнений методом прогонки Методом сеток с использованием метода прогонки найти решение граничных задач в точках. v 11
7.ppt