Лабораторная работа № 2 Тема:

Лабораторная работа № 2 Тема: Приближенное решение алгебраических уравнений

1. Отделение корней Рассмотрим уравнение , (1) где определена и непрерывна на некотором конечном или бесконечном интервале . Всякое значение , обращающее функцию в нуль, т. е. такое, что , называется корнем уравнения (1) или нулем функции . Теорема 1. Если непрерывная функция принимает значения разных знаков на концах отрезка , т. е. , то внутри этого отрезка содержится, по меньшей мере, один корень уравнения (1). Корень заведомо будет единственным, если производная существует и сохраняет постоянный знак внутри интервала . Процесс отделения корней начинается с установления знаков функции в граничных точках области ее существования. Затем определяют знаки функции в ряде промежуточных точек. 2

Пример 1. Отделить корни уравнения . Решение. Составим следующую таблицу: Таким образом, уравнение имеет три действительных корня, лежащих в интервалах 3

Если существует непрерывная производная и корни уравнения легко вычисляются, то для отделения корней уравнения (1) достаточно подсчитать знаки функции в точках нулей ее производной и в граничных точках. Пример 2. Отделить корни уравнения . Решение. при . Определим знаки функции: Следовательно, уравнение имеет три действительных корня, которые лежат в интервалах: 4

2. Оценка погрешности приближенного корня Теорема 2. Пусть – точный, а – приближенный корни уравнения (1), находящиеся на отрезке , причем при . В данном случае справедлива оценка: (2) Замечание 1. За можно взять наименьшее значение при . Замечание 2. Чтобы формула (2) давала более точные результаты, обычно сужают общий интервал , содержащий корень и его приближенное значение , и полагают . 5

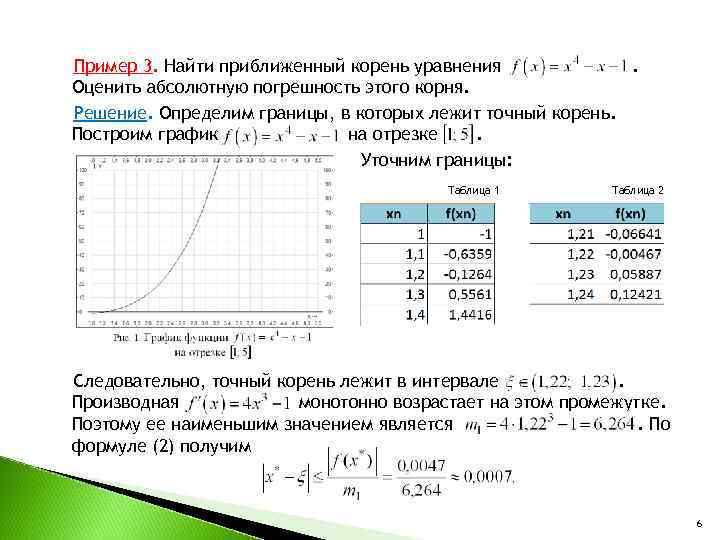
Пример 3. Найти приближенный корень уравнения . Оценить абсолютную погрешность этого корня. Решение. Определим границы, в которых лежит точный корень. Построим график на отрезке . Уточним границы: Таблица 1 Таблица 2 Следовательно, точный корень лежит в интервале . Производная монотонно возрастает на этом промежутке. Поэтому ее наименьшим значением является . По формуле (2) получим 6

3. Методы уточнения приближенного корня 3. 1. Метод хорд Рассмотрим более быстрый способ нахождения корня уравнения , лежащего на заданном отрезке , таком, что . Предполагаем, что непрерывна на . Пусть для определенности и . Тогда более рационально разделить отрезок в отношении . Это дает приближенное значение корня (3) где (4) Далее, применяя этот метод к тому из отрезков или , на концах которого функция имеет противоположные знаки, получим второе приближение корня и т. д. 7

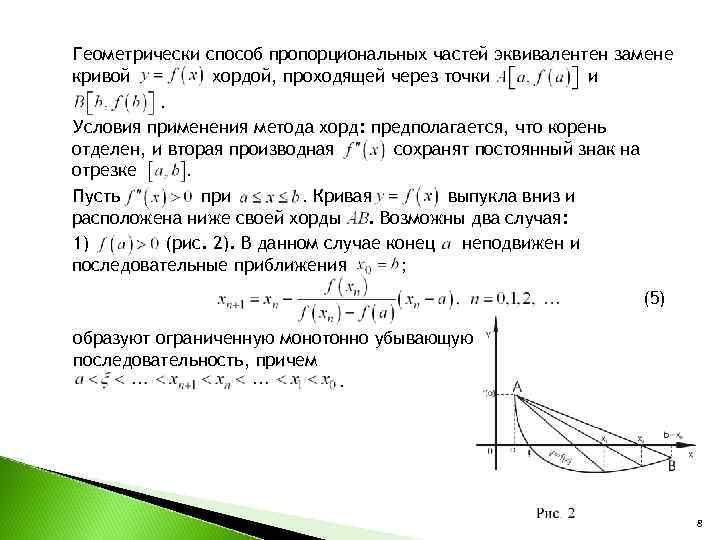
Геометрически способ пропорциональных частей эквивалентен замене кривой хордой, проходящей через точки . Условия применения метода хорд: предполагается, что корень отделен, и вторая производная сохранят постоянный знак на отрезке . Пусть при . Кривая выпукла вниз и расположена ниже своей хорды . Возможны два случая: 1) (рис. 2). В данном случае конец неподвижен и последовательные приближения ; (5) образуют ограниченную монотонно убывающую последовательность, причем 8

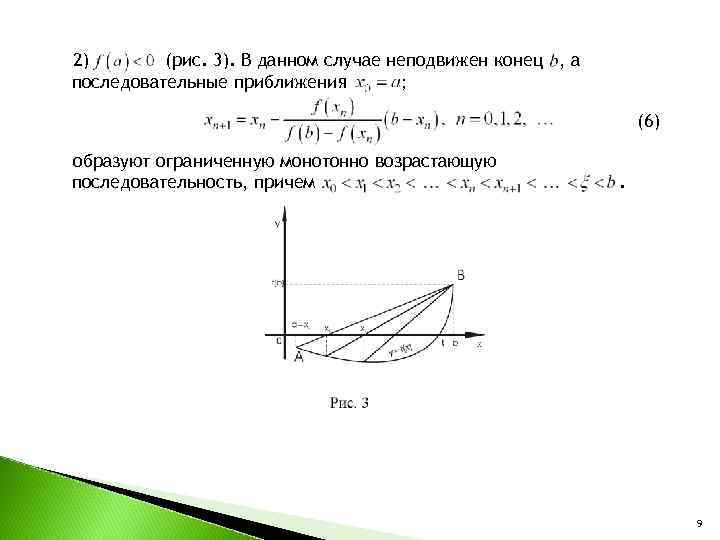
2) (рис. 3). В данном случае неподвижен конец , а последовательные приближения ; (6) образуют ограниченную монотонно возрастающую последовательность, причем 9

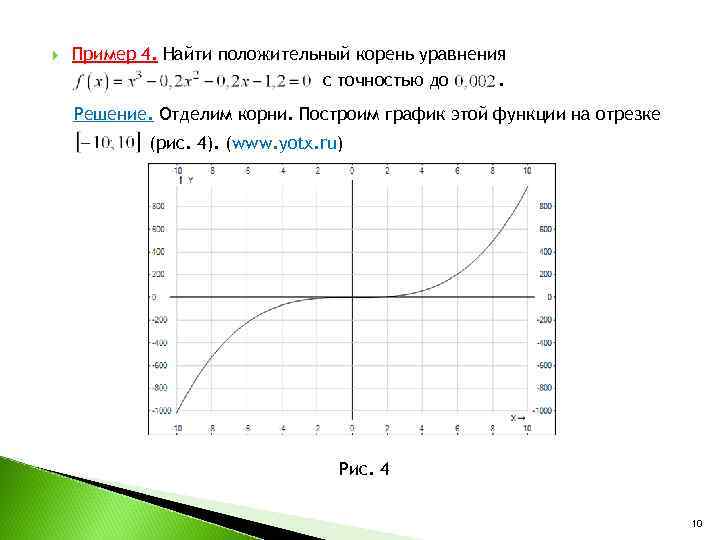
Пример 4. Найти положительный корень уравнения с точностью до . Решение. Отделим корни. Построим график этой функции на отрезке (рис. 4). (www. yotx. ru) Рис. 4 10

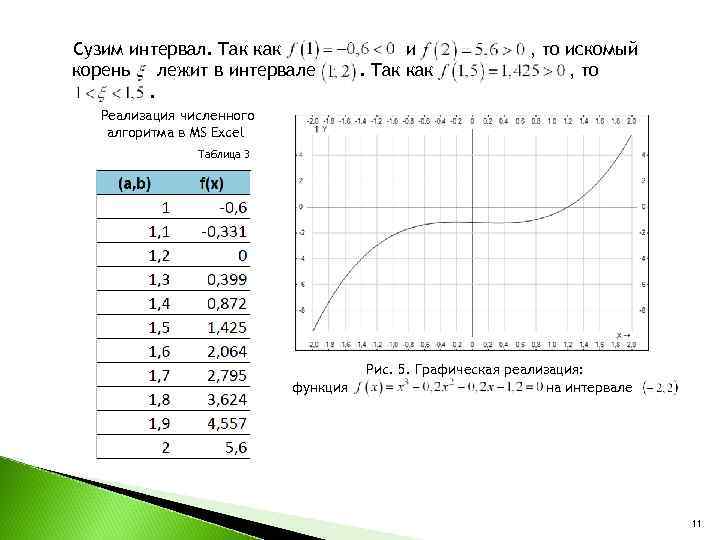
Сузим интервал. Так как и , то искомый корень лежит в интервале . Так как , то . Реализация численного алгоритма в MS Excel Таблица 3 Рис. 5. Графическая реализация: функция на интервале . 11

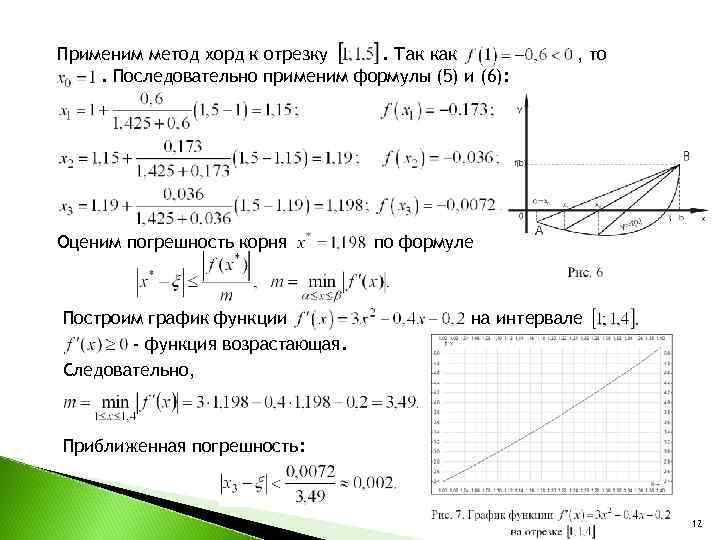
Применим метод хорд к отрезку . Так как , то . Последовательно применим формулы (5) и (6): Оценим погрешность корня по формуле Построим график функции на интервале - функция возрастающая. Следовательно, Приближенная погрешность: 12

Реализация метода хорд в MS Excel. Таблица 4 13

3. 2. Метод Ньютона Пусть – корень уравнения (1) отделен на отрезке , причем и непрерывны и сохраняют определенные знаки при . - --ое приближенное значение корня Уточнение корня осуществляется по методу Ньютона: (7) где Тогда, (8) 14

Теорема 3. Если , причем и отличны от нуля и сохраняют определенные знаки при , то, исходя из начального приближения , удовлетворяющего неравенству , можно вычислить методом Ньютона (формула (8)) единственный корень уравнения (1) с любой степенью точности. Замечание. При использовании метода Ньютона в качестве точки выбирается тот конец интервала , которому отвечает ордината того же знака, что и знак . Для оценки погрешности -го приближения корня можно воспользоваться общей формулой (2): 15

Пример 5. Вычислить методом Ньютона отрицательный корень уравнения с -ю верными знаками. Решение. Определим интервал, в котором находится корень. Реализация численного Графический способ алгоритма в MS Excel нахождения интервала Таблица 5 16

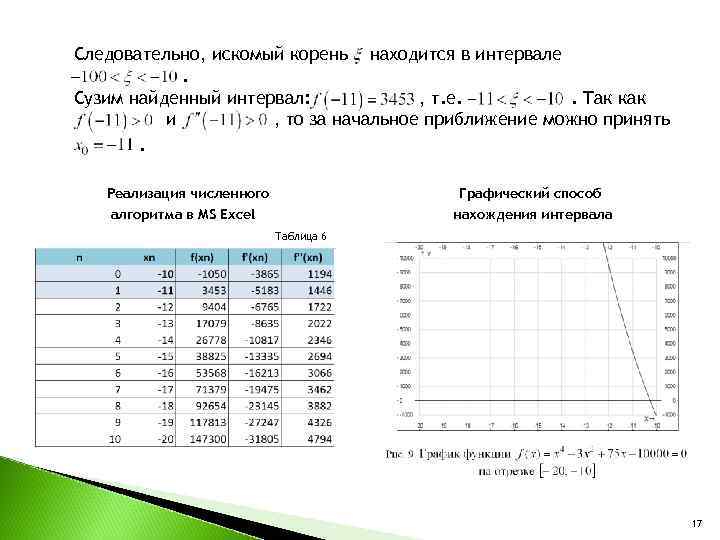
Следовательно, искомый корень находится в интервале . Сузим найденный интервал: , т. е. . Так как и , то за начальное приближение можно принять . Реализация численного Графический способ алгоритма в MS Excel нахождения интервала Таблица 6 17

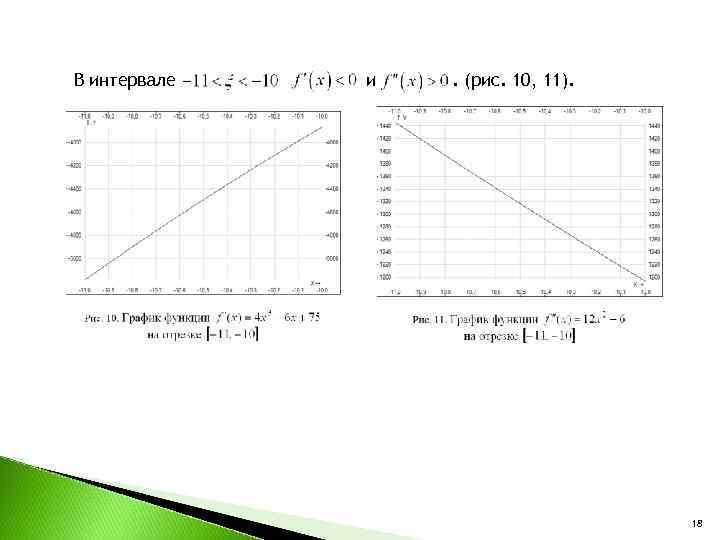
В интервале и . (рис. 10, 11). 18

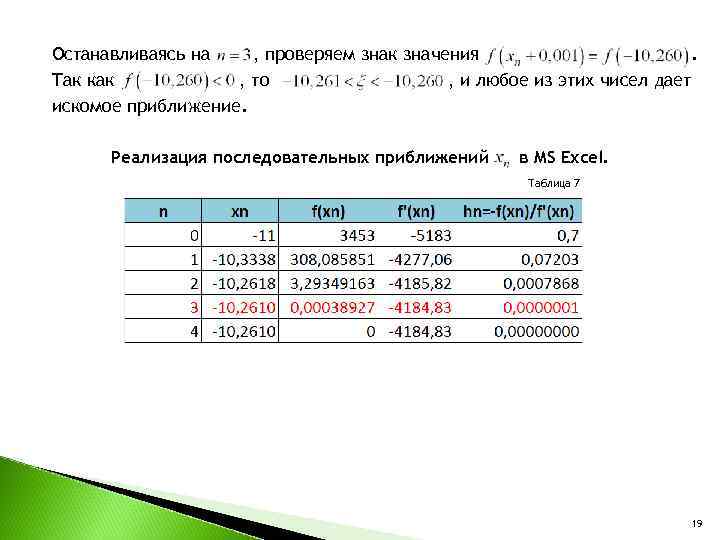
Останавливаясь на , проверяем знак значения . Так как , то , и любое из этих чисел дает искомое приближение. Реализация последовательных приближений в MS Excel. Таблица 7 19

Задание № 2 Тема: Приближенное решение алгебраических уравнений 1. Отделить корни уравнения (графически или аналитически), найти отрезок, на котором лежит один из корней. 2. Найти отличный от нуля корень уравнения с четырьмя верными знаками после запятой методом хорд и методом Ньютона. 20