Лабораторная работа 2 19 вариант Задание

Зарегистрируйтесь, чтобы просмотреть полный документ!

РЕГИСТРАЦИЯ

Лабораторная работа 2 19 вариант

Задание

Алгоритм к решению задачи

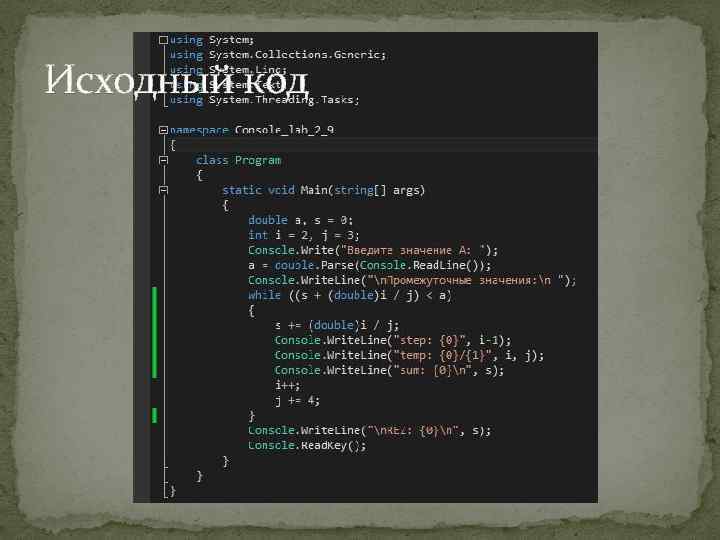
Исходный код

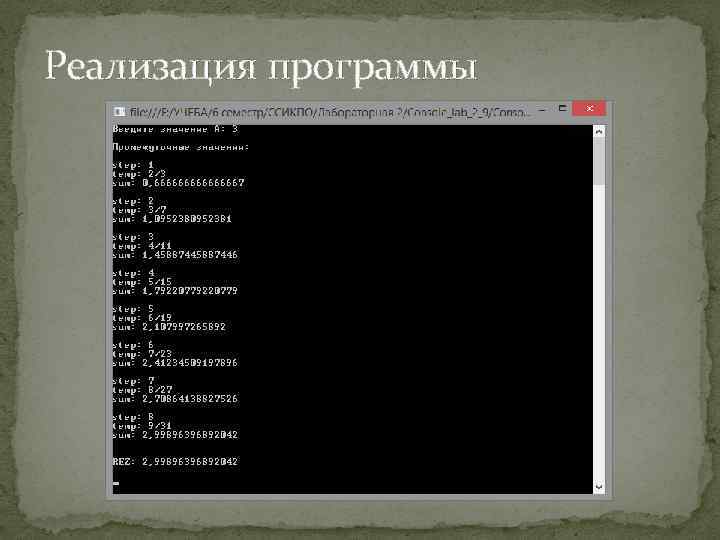
Реализация программы

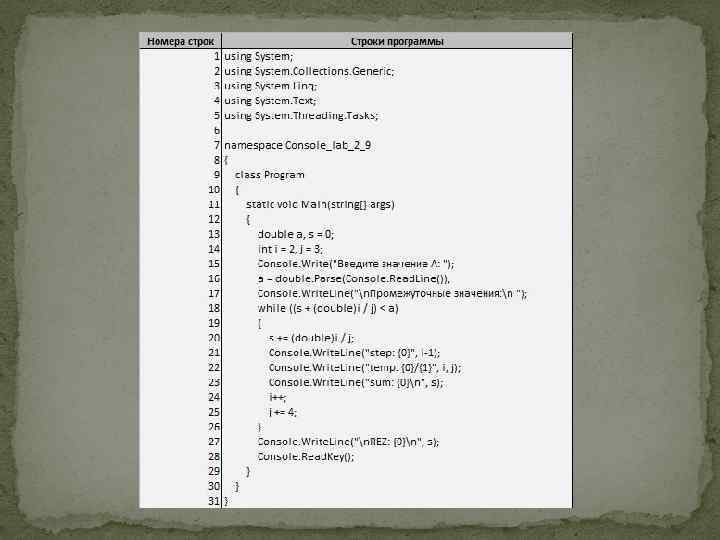
Объединение участков программы

Граф управления программой Количество дуг m = 4 Количество вершин n = 4 Цикломатическое число Маккейба: Z=m–n+2=4– 4+2=2

Оценка структурной сложности Критерий 1 Для составленного управляющего графа можно выделить 2 маршрута: M 1 = 1 -2 -3 -4 (P 1 = 2) M 2 = 1 -2 -3 -4 (P 2 = 1) Результат критерия: S 1 = 2 + 1 = 3

Критерий 2 Число вершин ветвления составляет 1, отсюда: Z = 1 + 1 = 2 (маршрута на графе) Выделяем эти маршруты: Ациклический маршрут: M 1 = 1 -2 -3 -4 (P 1 = 1) Циклический маршрут: M 2 = 3 -2 -3 (P 2 = 2) Результат критерия: S 2 = 1 + 2 = 3

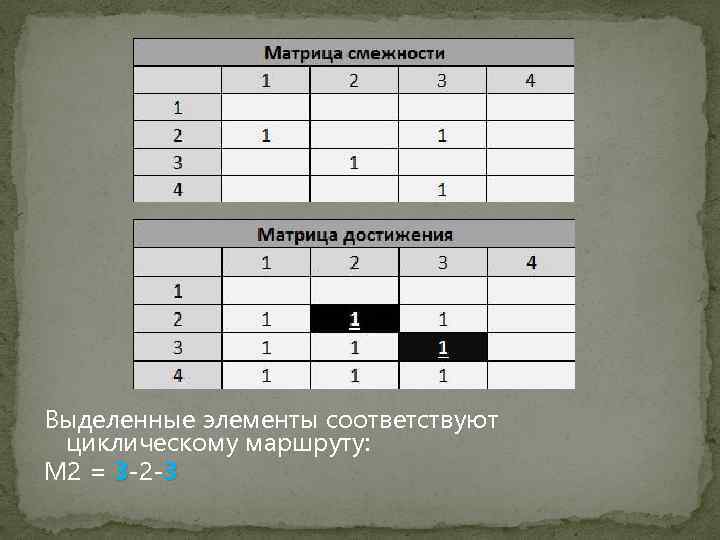
Выделенные элементы соответствуют циклическому маршруту: M 2 = 3 -2 -3

Критерий 3 В соответствии с этим критерием нужно выделить все возможные маршруты. В данном случае существует 2 маршрута: M 1 = 1 -2 -3 -4 (P 1 = 2) M 2 = 1 -2 -3 -4 (P 2 = 1) Результат критерия: S 3 = 2 + 1 = 3

Выводы Исходя из полученных результатов расчета метрик структурной сложности по первому (S 1 = 3), по второму (S 2 = 3), по третьему (S 3 = 3) можно сделать вывод, что программа простая и содержит всего один оператор ветвления. Другими словами программа не имеет особой алгоритмической сложности. Исходя из оценки по метрике Маккейба (Z = 2), можно в программе 2 независимых контура, т. е. 2 маршрута выполнения программы. Значение не превышает 10, что свидетельствует о незначительной сложности программы. В данном случае задание очень простое и ее реализация сокращена до одного оператора ветвления, что очень упрощает исходную программу во всех смыслах. Поэтому в данном случае

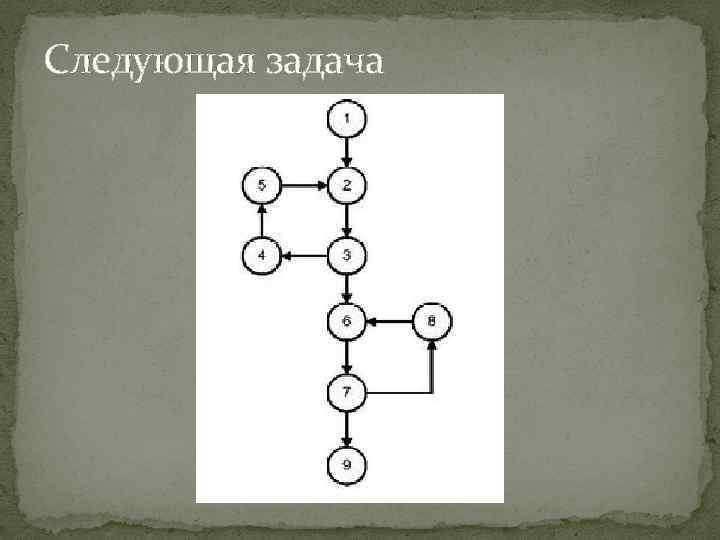
Следующая задача

Анализ управляющего графа Количество дуг m = 10 Количество вершин n = 9 Цикломатическое число Маккейба: Z = m – n + 2 = 10 – 9 + 2 = 3

Оценка структурной сложности Критерий 1 Для составленного управляющего графа можно выделить 2 маршрута: M 1 = 1 -2 -3 -4 -5 -2 -3 -6 -7 -9 (P 1 = 3) M 2 = 1 -2 -3 -6 -7 -8 -6 -7 -9 (P 2 = 3) Результат критерия: S 1 = 3 + 3 = 6

Критерий 2 Число вершин ветвления составляет 2, отсюда: Z = 2 + 1 = 3 (маршрута на графе) Выделяем эти маршруты: Ациклический маршрут: M 1 = 1 -2 -3 -6 -7 -9 (P 1 = 2) Циклический маршрут: M 2 = 2 -3 (P = 1) и M 3 = 6 -7 (P = 1) Результат критерия: S 2 = 2 + 1 = 4

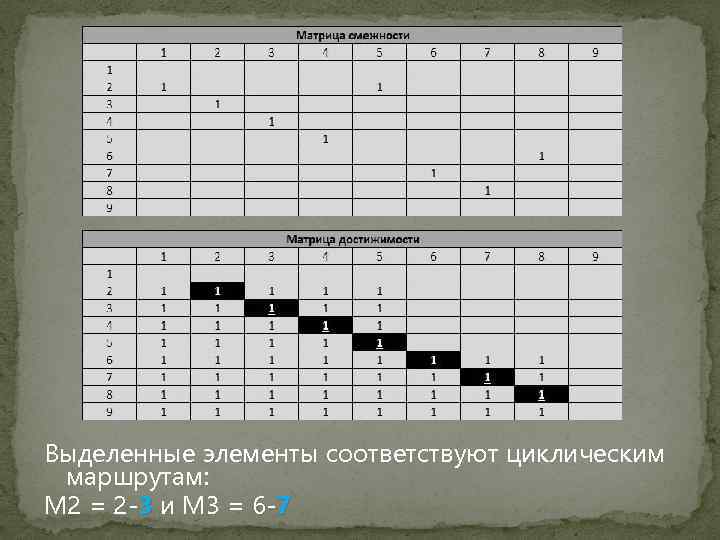
Выделенные элементы соответствуют циклическим маршрутам: M 2 = 2 -3 и M 3 = 6 -7

Критерий 3 Выделяем все возможные маршруты. В данном случае существует 4 маршрута: M 1 = 1 -2 -3 -6 -7 -9 (P 1=2) M 2 = 1 -2 -3 -4 -5 -2 -3 -6 -7 -9 (P 2=3) M 3 = 1 -2 -3 -6 -7 -8 -6 -7 -9 (P 3=3) M 4 = 1 -2 -3 -4 -5 -2 -3 -6 -7 -8 -6 -7 -9 (P 4=4) Результат критерия: S 3 = P 1 + P 2 + P 3 + P 4 = 2 + 3 + 4 = 12

Выводы Исходя из полученных результатов расчета метрик структурной сложности по первому (S 1 = 6), по второму (S 2 = 4), по третьему (S 3 = 12) можно сделать вывод, что программа обладает не высокой алгоритмической сложностью и содержит 2 условных оператора. Исходя из оценки по метрике Маккейба (Z = 3), можно в программе 3 независимых контура, т. е. 3 маршрута выполнения программы. Значение не превышает 10, что свидетельствует о незначительной сложности программы.

Скачать презентацию Лабораторная работа 2 19 вариант Задание

lab2_9_prez.pptx

Количество слайдов: 20