071ebc21a786bd8dfa654e873b8b385d.ppt
- Количество слайдов: 37


Лаборатория нейтронных физикохимических исследований (ЛНФИ) Laboratory for neutron physicochemical investigations (LNPI) Группа химической физики и спектроскопии: Корпус 7 - Комплекс оборудования для синтеза и аттестации атомных кластеров и наноструктур (эндофуллерены и производные, углеродные композиты феррочастиц и др. ) Группа нейтронных исследований надатомных структур: Реактор ВВРМ - Дифрактометр “Мембрана-2” Модуляционный спин-эхо спектрометр









Нейтроны: энергии E 1 э. В, длины волн 0. 03 нм Мощный инструмент анализа структуры и динамики атомной и магнитной q - атомного размера q энергия E ~ k. T q магнитный момент q проникающая способность - десятки см Тепловые и холодные нейтроны: E ~ 0. 01 -0. 1 э. В, Е < 0. 01 э. В Энергетический спектр рассеянных нейтронов - динамика на атомном уровне волновые свойства: v преломление на границе сред v полное внутреннее отражение v дифракция, рассеяние на малые углы Взаимодействие с ядрами Информация о строении водородсодержащих и других соединений из элементов с близкими атомными номерами (изотопы) Получить подобные данные из рентгеновской дифракции сложно!!!

Медленный нейтрон - ядерное взаимодействие + магнитное взаимодействие с электронной оболочкой остальные весьма слабые: Швингера - при скорости нейтрона V в поле ядра E на нейтрон действует поле [EV]/c, n-e-взаимодействие Рассеяние силовым полем ядра или через образование промежуточного возбужденного ядра с последующим распадом Медленные нейтроны - обычно два канала распада промежуточного ядра: радиационный захват и резонансное упругое рассеяние (суммарная кинетическая энергия не меняется при рассеянии) Интерференция потенциального упругого и резонансного рассеяния Для медленных нейтронов сечение почти не зависит от их энергии Теория Взаимодействие нейтронов с веществом - рассеяние нейтрона на ядре без спина: потенциал взаимодействия V(r) зависит только от расстояния r между частицами, и задача решается в системе центра масс.

Волновая функция падающего нейтрона массой m и энергией E - плоская волна exp(ikor) с волновым вектором ko вдоль скорости нейтрона, ko=(2 m. E/ 2)1/2. k n, k 0 k q k 0

На больших расстояниях нет взаимодействия с ядром Падающая + рассеянная волна (r)r = exp(ikoz) + [f( , k)/r]exp(ikr) Амплитуда f( , k) зависит от полярного угла в системе координат с осью Z вдоль ko. Сечение ядра в элемент телесного угла d =2 sin d : d = f( , k) 2 d Амплитуда - ряд по собственным функциям орбитального момента нейтрона l - интеграла движения для центрального потенциала: f( , k) = (2 ik)-1 (2 l+1)[exp(2 i l) - 1]Pl (cos ). Pl - полиномы Лежандра, а l(k) - фазовые сдвиги рассеянных волн. Длина волны > 10 -9 см >> ro ~ 10 -12 см - радиуса действия потенциала ядра Сохраняется только слагаемое с l = 0 Рассеяние изотропно, f(k)=[sin o(k)]/k. При малых волновых векторах l(k)~k 2 l+1, f(k) o(k)/k limf(k)k 0=const= b b - длина рассеяния ядра - фазовый сдвиг рассеянной волны в единицах длины

У большинства ядер b > 0, у ряда элементов b < 0 (H, Li, Ti) Изменение b - замещение изотопов - преимущество в сравнении с рентген. и оптическими методами - вариация контраста!!! Ядро без спина: сечение d = b 2 d Ядро имеет спин I - две длины рассеяния b+, b Параллельная и антипараллельная ориентации спинов частиц суммарный спин ядра и нейтрона J=I+1/2 , J=I-1/2 d =[b+2(I+1)/(2 I+1)+b 2 I/(2 I+1)]d дополнительные возможности контрастирования !!! Ансамбль ядер: порядок расположения, общность физических свойств - интерференция волн - когерентное сечение coh Нарушение порядка - интерференция исчезает: некогерентное рассеяние от ядер inc Полное сечение = coh + inc

Изотопическая некогерентность: Случайное распределение изотопов по ядрам Спиновая некогерентность: Случайная взаимная ориентация спинов частиц + вероятность переворота спина нейтрона при рассеянии 2/3 сечения некогер. рассеяния - переворот спина нейтрона, 1/3 - хаотическая взаимной ориентации спинов нейтрона и ядра Поляризация нейтронов и ядер устраняет первую причину Реализуется второй механизм Когерентность и некогерентность проявляется при магнитном взаимодействии нейтрона с электронными оболочками Магнитный момент нейтрона = 2 NSn противоположен его спину Sn = -1. 913 - магнитный момент в ядерных магнетонах N Потенциал магнитного взаимодействия нейтрона и атома V=(1/c) A(r, rl) j(rl) Векторный потенциал A(r, rl) = [ (rl-r)]/ rl-r 3 создан моментом нейтрона (координата r) в позиции электрона rl, и плотностью электронного тока j(rl) Электронный ток j(rl) - сумма орбитальной и спиновой составляющих

Рассеяние на свободном ядре - задача в системе центра масс Химически связанные частицы (молекула, кристалл): b = a(A+1)/A а - длина для свободного ядра, А - его атомная масса У протона длина рассеяния возрастает в 2 раза! Связанный центр - обмен энергией с коллективными степенями свободы - неупругое рассеяние! При рассеянии нейтрона на свободном ядре, оно испытывает отдачу, энергия нейтрона меняется На связанном ядре рассеяние может быть без изменения энергии нейтрона (упруго), если возбуждение коллективных движений невозможно – дифракции Нейтрон взаимодействует с ансамблем ядер: сферические волны Суперпозиция волн - первое приближение + вторичное излучение Первое приближение: амплитуда упругого рассеяния ансамблем из N атомов A(q) = bi exp(iqri) bi -длина рассеяния i-го ядра с координатой ri Сечение d (q)/d =A(q)*

Контрастирование, H D: длины H и D разные по величине и знаку, bcoh. H= 0, 374 10 -12 см, bcoh. D= +0, 667 10 -12 см Объем V, n рассеивателей с длинами bi в точках ri. сечение d coh/d = bibj<exp[iq(ri-rj)]>. Плотность (r) = (r-ri), концентрация C = (n/V) (r), плотность длины рассеяния A = b (r), Фурье-образы (q)= (r)eiqrdr, C(q)=(n/V) (q), A(q)=b (q) Сечение d coh/d =b 2< (q) (-q)>. Два типах рассеивателей с удельными объемами v 1, v 2 и длинами b 1, b 2 Сечение задано плотностью рассеивателей одного типа (первого). "Кажущаяся" длина для них равна =b 1 -(v 1/v 2 2 ) b

Сечение → Фурье-образ корреляционной функции плотности d coh/d = 2< 1(q) 1(-q)> G(R)exp(iq. R)d. R G(R) = < 1(r) 1(r+R)> - коррелятор отклонения плотности частиц 1(r) = 1(r) - < 1(r)> от среднего < 1(r)> для частиц на расстоянии R Контраст на масштабе >> межатомного расстояния (раствор макромолекул) Избирательное изучение корреляций частиц статических и динамических
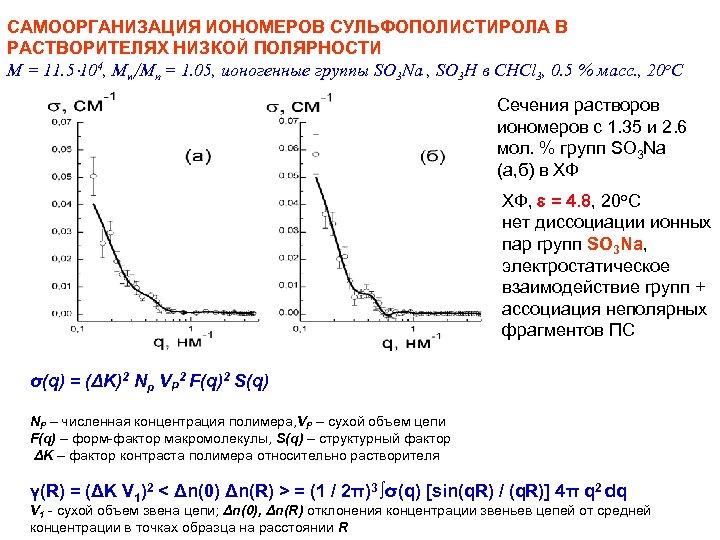
САМООРГАНИЗАЦИЯ ИОНОМЕРОВ СУЛЬФОПОЛИСТИРОЛА В РАСТВОРИТЕЛЯХ НИЗКОЙ ПОЛЯРНОСТИ M = 11. 5 104, Mw/Mn = 1. 05, ионогенные группы SO 3 Na , SO 3 H в CHCl 3, 0. 5 % масс. , 20 о. С Сечения растворов иономеров с 1. 35 и 2. 6 мол. % групп SO 3 Na (а, б) в ХФ ХФ, = 4. 8, 20 o. C нет диссоциации ионных пар групп SO 3 Na, электростатическое взаимодействие групп + ассоциация неполярных фрагментов ПС σ(q) = (ΔK)2 Np VP 2 F(q)2 S(q) NP – численная концентрация полимера, VP – сухой объем цепи F(q) – форм-фактор макромолекулы, S(q) – структурный фактор ΔK – фактор контраста полимера относительно растворителя γ(R) = (ΔK V 1)2 < Δn(0) Δn(R) > = (1 / 2π)3 ∫σ(q) [sin(q. R) / (q. R)] 4π q 2 dq V 1 - сухой объем звена цепи; Δn(0), Δn(R) отклонения концентрации звеньев цепей от средней концентрации в точках образца на расстоянии R
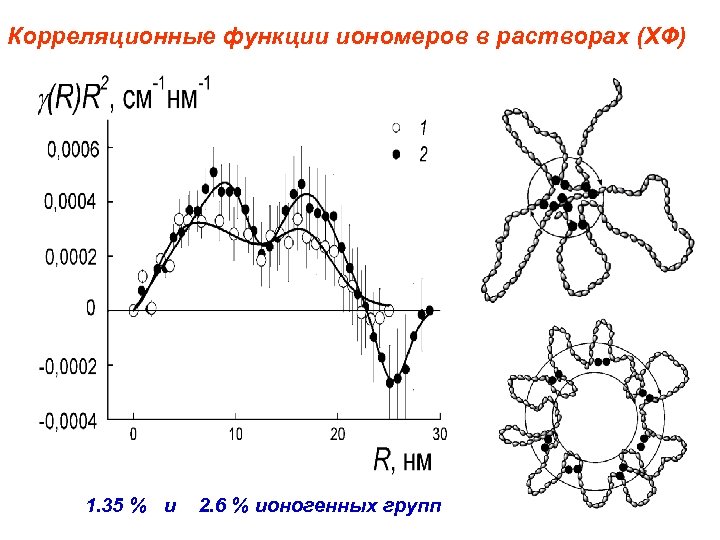
Корреляционные функции иономеров в растворах (ХФ) 1. 35 % и 2. 6 % ионогенных групп

Структура и размеры “эффективных” цепей иономеров 0. 5 5. 8 мол. % групп SO 3 Na в D-толуоле Конформация клубка гауссова даже при степени сульфирования 5. 8 мол. % расстояние между группами по цепи ~ длины сегмента Самоорганизация во вторичные структуры из 4 5 “эффективных цепей” Пары “эффективные” цепи из 7 молекул = 0. 5 мол. % = 1. 35 мол. % плотные кластеры = 5. 8 мол. %
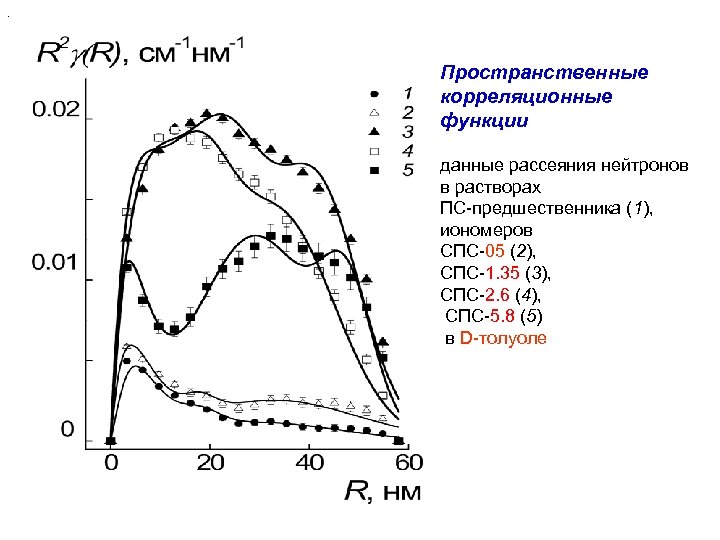
. Пространственные корреляционные функции данные рассеяния нейтронов в растворах ПС-предшественника (1), иономеров СПС-05 (2), СПС-1. 35 (3), СПС-2. 6 (4), СПС-5. 8 (5) в D-толуоле
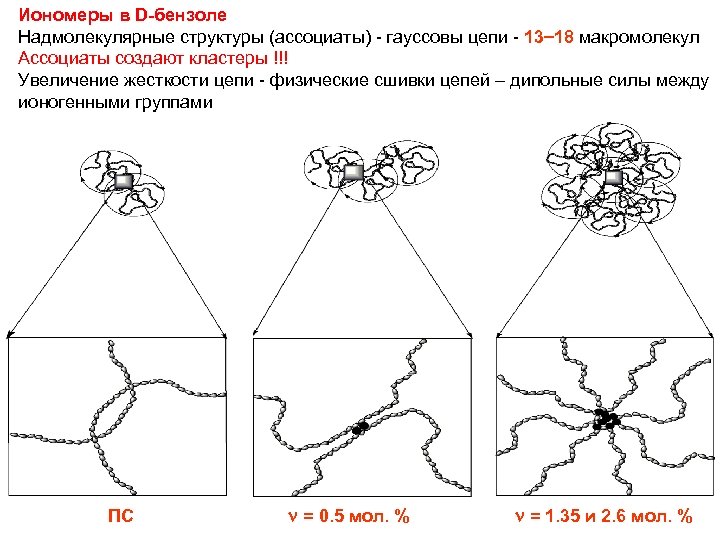
Иономеры в D-бензоле Надмолекулярные структуры (ассоциаты) - гауссовы цепи - 13 18 макромолекул Ассоциаты создают кластеры !!! Увеличение жесткости цепи - физические сшивки цепей – дипольные силы между ионогенными группами ПС = 0. 5 мол. % = 1. 35 и 2. 6 мол. %
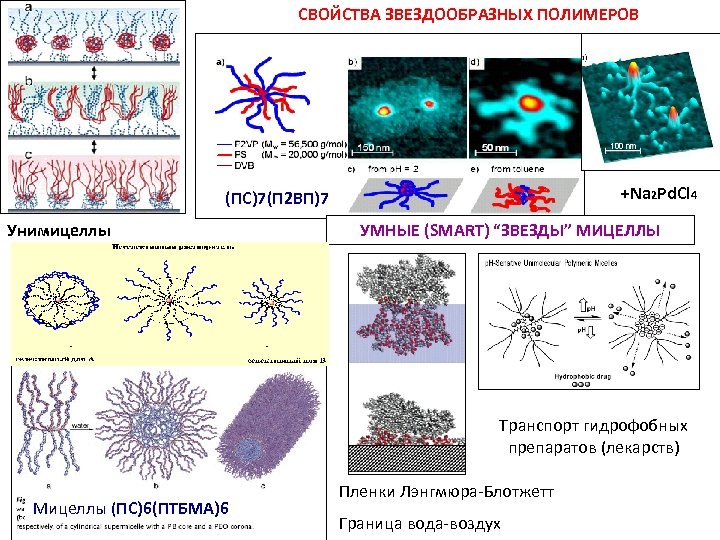
СВОЙСТВА ЗВЕЗДООБРАЗНЫХ ПОЛИМЕРОВ +Na 2 Pd. Cl 4 (ПС)7(П 2 ВП)7 Унимицеллы УМНЫЕ (SMART) “ЗВЕЗДЫ” МИЦЕЛЛЫ Транспорт гидрофобных препаратов (лекарств) Мицеллы (ПС)6(ПТБМА)6 Пленки Лэнгмюра-Блотжетт Граница вода-воздух
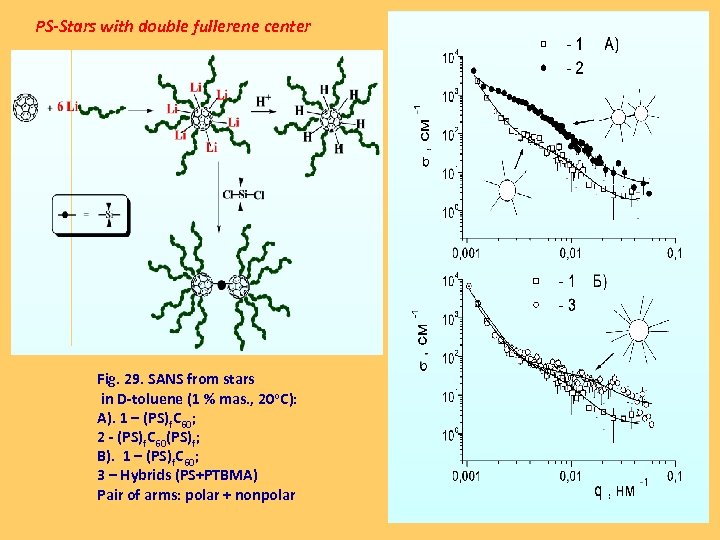
PS-Stars with double fullerene center Fig. 29. SANS from stars in D-toluene (1 % mas. , 20 o. C): A). 1 – (PS)f. C 60; 2 - (PS)f. C 60(PS)f; B). 1 – (PS)f. C 60; 3 – Hybrids (PS+PTBMA) Pair of arms: polar + nonpolar
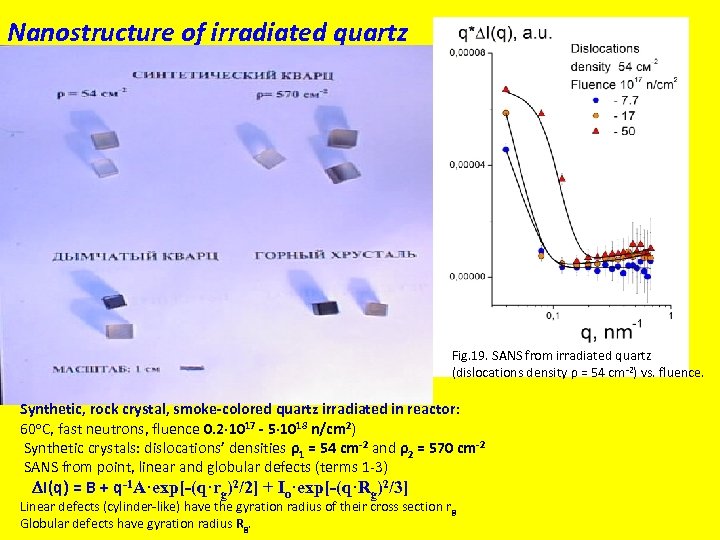
Nanostructure of irradiated quartz Fig. 19. SANS from irradiated quartz (dislocations density ρ = 54 cm-2) vs. fluence. Synthetic, rock crystal, smoke-colored quartz irradiated in reactor: 60 o. C, fast neutrons, fluence 0. 2∙ 1017 - 5∙ 1018 n/cm 2) Synthetic crystals: dislocations’ densities ρ1 = 54 cm-2 and ρ2 = 570 cm-2 SANS from point, linear and globular defects (terms 1 -3) I(q) = B + q-1 A·exp[-(q·rg)2/2] + Io·exp[-(q·Rg)2/3] Linear defects (cylinder-like) have the gyration radius of their cross section r g Globular defects have gyration radius Rg.
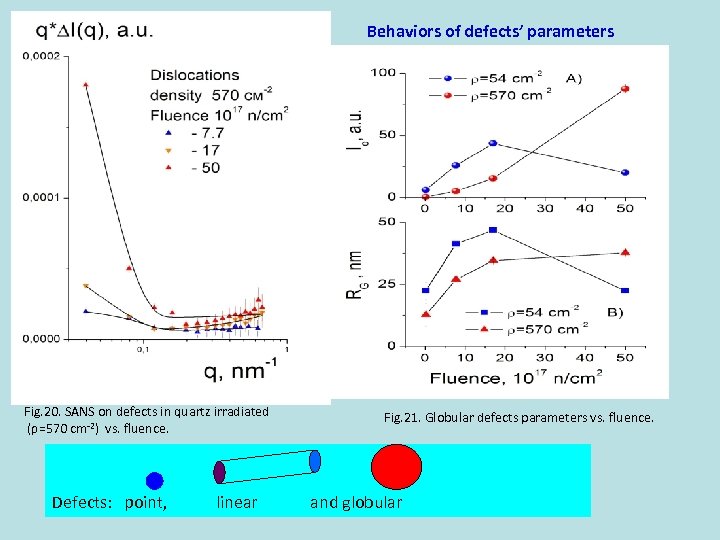
Behaviors of defects’ parameters Fig. 20. SANS on defects in quartz irradiated (ρ=570 cm-2) vs. fluence. Defects: point, linear Fig. 21. Globular defects parameters vs. fluence. and globular

MINERAL FIBRES - NATURAL AND INDUSTRIAL SURFACE AND VOLUME DEFECTS IN BASALTIC FIBRES BY SANS Russian Enterprises & “Rockwool”, “Paros”, “Isoroc” v Nontraditional amorphous materials for heat and acoustic isolation (mechanical engineering, space technology, motor industry, construction) v Developed solid-gaze interface ( 1 m 2/g, thickness 1 -10 micron) v Ecologically safe materials v Huge stocks of basalt in the Earth's crust Basalt technologies: Ømelting at temperatures > 1000 o. C, Øaddition of binding components, Ødispersion process (extrusion, inflating by a jet of air or steam) Composition: 51– 47% Si. O 2, 14 – 12% Al 2 O 3, 5 – 2 % Fe 2 O 3, 12 – 7 % Fe. O, 10 – 4 % Mg. O, 10 – 8 % Ca. O, 3 – 2 % Na 2 O, 2 – 0 % K 2 O, 3 – 1 % Ti. O 2, 0. 8 – 0. 4 % P 2 O 5 %, 0. 3 – 0. 1 % Mn. O 2, 3 – 0 % H 2 O
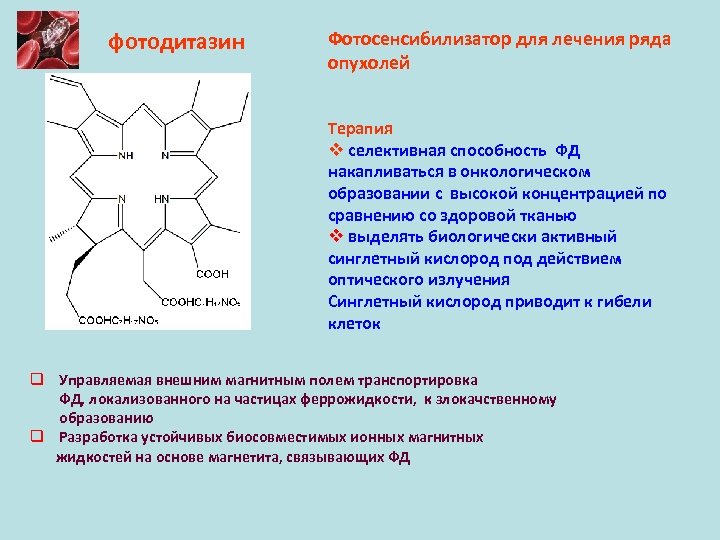
фотодитазин Фотосенсибилизатор для лечения ряда опухолей Терапия v селективная способность ФД накапливаться в онкологическом образовании с высокой концентрацией по сравнению со здоровой тканью v выделять биологически активный синглетный кислород под действием оптического излучения Синглетный кислород приводит к гибели клеток q Управляемая внешним магнитным полем транспортировка ФД, локализованного на частицах феррожидкости, к злокачственному образованию q Разработка устойчивых биосовместимых ионных магнитных жидкостей на основе магнетита, связывающих ФД
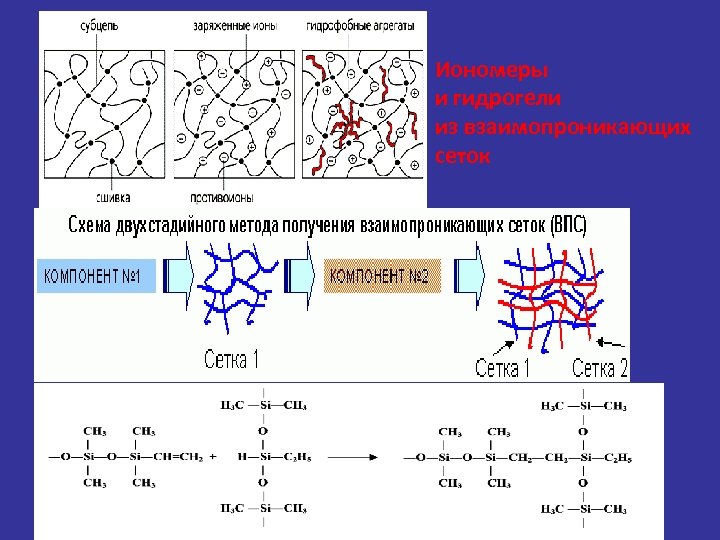
Иономеры и гидрогели из взаимопроникающих сеток
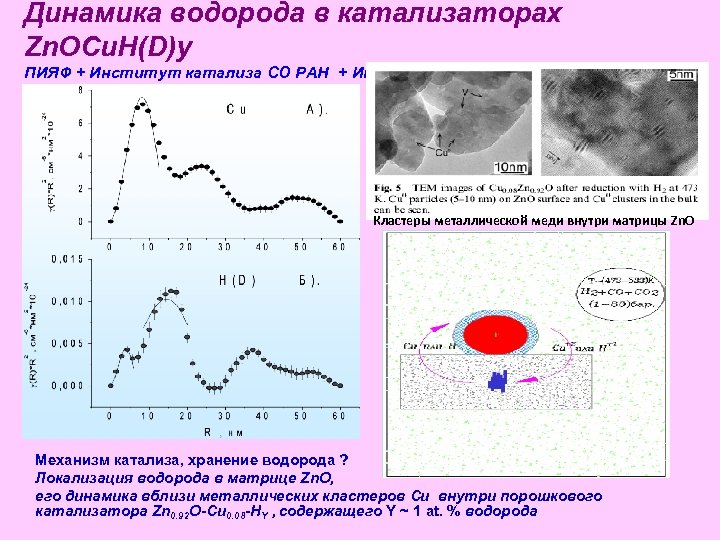
Динамика водорода в катализаторах Zn. OCu. H(D)y ПИЯФ + Институт катализа СО РАН + Институт физики твердого тела АН Венгрии + Университет Амстердама Кластеры металлической меди внутри матрицы Zn. O Механизм катализа, хранение водорода ? Локализация водорода в матрице Zn. O, его динамика вблизи металлических кластеров Cu внутри порошкового катализатора Zn 0. 92 O-Cu 0. 08 -HY , содержащего Y ~ 1 at. % водорода

Диффузия и релаксационные моды водородной оболочки Быстрая диффузия в матрице и медленная вблизи кластера PEVEN(t) = ASH∙exp(-t/τSH) + ALO∙exp(-t/τLO) Константы диффузии при 370 K: DFAST ~ 1∙ 10 -5 cm 2/c DSLOW ~ 7∙ 10 -8 cm 2/с Амплитуды ASH, ALO и времена релаксации мод τSH, τLO – функции температуры Энергии активации диффузии: ESH ~ 0. 08 e. V (быстрая мода) ESH ~ 0. 06 e. V (медленная мода)
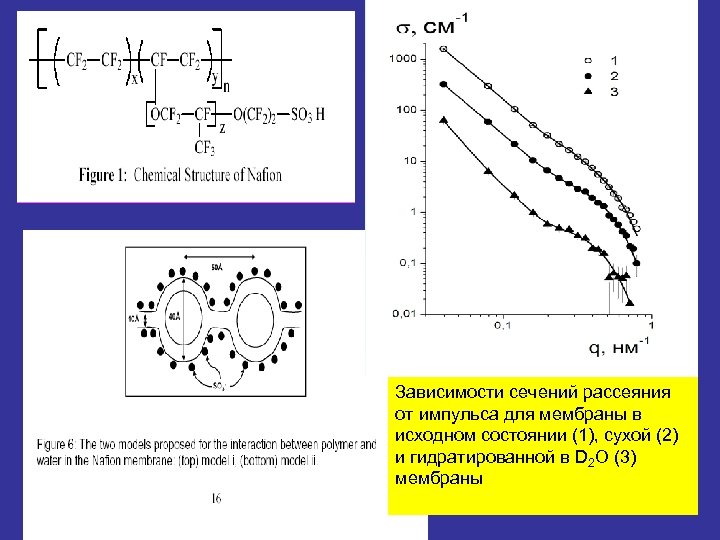
Зависимости сечений рассеяния от импульса для мембраны в исходном состоянии (1), сухой (2) и гидратированной в D 2 O (3) мембраны

ПАРАМЕТРЫ Газовая смесь: 4 atm. 3 He + 2 atm. CF 4 2 D-детектор 200× 200 mm 2 Материнская плата с предусилетелями, линиями задержки и системой газонаполнения Эффективность 70% (λ = 0. 3 нм) Пространственное разрешение FWHM ≤ 1. 5 mm (вдоль непрерывной координаты Y) FWHM = 2 mm (вдоль дискретной координаты X) Дифференциальная нелинейность ± 10% Картина рассеяния (λ = 0. 3 нм) на фторопласте (CF 2)n изотропном и при одноосном растяжении
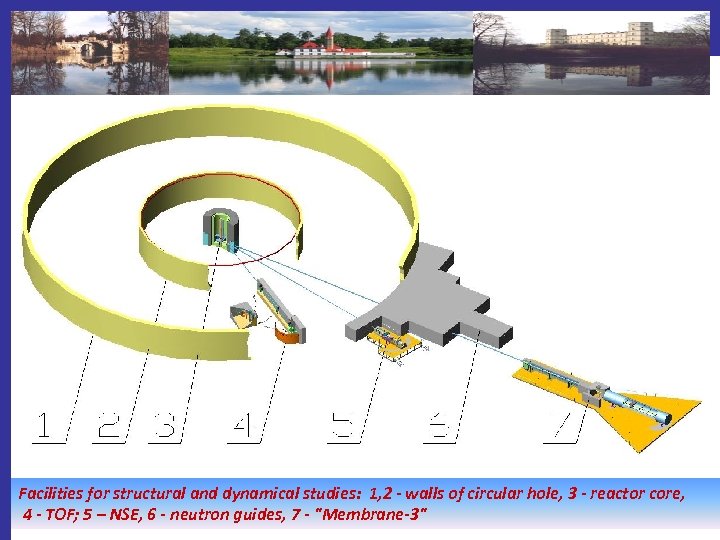
Facilities for structural and dynamical studies: 1, 2 - walls of circular hole, 3 - reactor core, 4 - TOF; 5 – NSE, 6 - neutron guides, 7 - "Membrane-3"
071ebc21a786bd8dfa654e873b8b385d.ppt