a9d668d514f42d27f5d24811313a2906.ppt
- Количество слайдов: 2

Lab 3 -8 In designing your recycling business for efficiency, you need to know how best to allocate your equipment budget. A part of this process is determining how many of each major piece of equipment should be purchased. For this project you need to decide how many glass recycling machines and plastic recycling machines to buy. You need to consider each machine type's capacity, floor space requirements, and cost, as given in the following table: Recycling Machine Glass Plastic Capacity 3. 2 tons/hour 1. 6 tons/hour Floor Space 180 sq. ft. 205 sq. ft. Cost $14, 500. 00 $19, 600. 00 1. Translate the following constraints into a system of linear inequalities. Let G represent the number of glass recycling machines (x for our calculator) and P the number of plastic recycling machines (y for our calculator). a. C 1: The facility needs to be able to process at least 10 tons of glass per hour. b. C 2: The facility needs to be able to process at least 7 tons of plastic per hour. c. C 3: The total floor space available for the machines is 3400 square feet d. C 4: The budget for recycling machines is $300, 000 2. Your objective is to maximize the total value of recycled material that can be processed in one hour. Assuming recycled glass has a value of $112 per ton and recycled plastic has a value of $235 per ton, write an equation for the value of recycled material that is produced in one hour by G glass recycling machines and P plastic recycling machines (assuming that all machines work at full capacity) V= P 3. Write the linear programming problem in the standard format (Y ≥ mx + b) that we have seen in activities 3. 6 and 3. 7 Maximize V = Subject to: C 1: C 2: C 3: C 4: G 4. Use your calculator and sketch the feasible region on the graph above, determine the corner points and determine the maximum value of recycled material. Use the table on back to list the corner points.
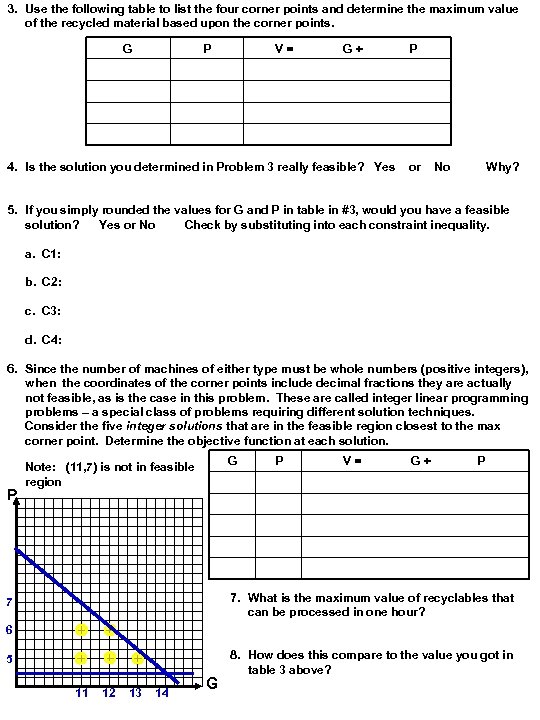
3. Use the following table to list the four corner points and determine the maximum value of the recycled material based upon the corner points. G P V= G+ 4. Is the solution you determined in Problem 3 really feasible? Yes P or No Why? 5. If you simply rounded the values for G and P in table in #3, would you have a feasible solution? Yes or No Check by substituting into each constraint inequality. a. C 1: b. C 2: c. C 3: d. C 4: 6. Since the number of machines of either type must be whole numbers (positive integers), when the coordinates of the corner points include decimal fractions they are actually not feasible, as is the case in this problem. These are called integer linear programming problems – a special class of problems requiring different solution techniques. Consider the five integer solutions that are in the feasible region closest to the max corner point. Determine the objective function at each solution. P G Note: (11, 7) is not in feasible region P V= G+ P 7. What is the maximum value of recyclables that can be processed in one hour? 7 6 5 11 12 13 14 G 8. How does this compare to the value you got in table 3 above?
a9d668d514f42d27f5d24811313a2906.ppt