LA VALIDAZIONE DEI METODI DI ANALISI CHIMICA METODI















































































1444-14_2_validation_statistics_ru_2.ppt
- Количество слайдов: 85
 LA VALIDAZIONE DEI METODI DI ANALISI CHIMICA
LA VALIDAZIONE DEI METODI DI ANALISI CHIMICA
 METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI VALIDAZIONE DEI METODI p.to 5.4.5 Il laboratorio deve validare : i metodi non normalizzati i metodi sviluppati/progettati dal laboratorio i metodi normalizzati utilizzati al di fuori del proprio scopo e campo di applicazione i metodi risultanti da estensioni e modifiche apportate metodi normalizzati per confermare che i metodi siano adatti all’utilizzazione prevista. LA VALIDAZIONE E’ LA CONFERMA ATTRAVERSO ESAME E L’APPORTO DI EVIDENZA OGGETTIVA CHE I REQUISITI PARTICOLARI PER L’UTILIZZAZIONE PREVISTA DEL METODO SIANO SODDISFATTI La validazione deve essere estesa in modo da soddisfare le esigenze di una data applicazione o di un campo di applicazione. Il laboratorio deve registrate i risultati ottenuti, le procedure utilizzate per la validazione, cosi pure una dichiarazione circa l’idoneità del metodo utilizzato.
METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI VALIDAZIONE DEI METODI p.to 5.4.5 Il laboratorio deve validare : i metodi non normalizzati i metodi sviluppati/progettati dal laboratorio i metodi normalizzati utilizzati al di fuori del proprio scopo e campo di applicazione i metodi risultanti da estensioni e modifiche apportate metodi normalizzati per confermare che i metodi siano adatti all’utilizzazione prevista. LA VALIDAZIONE E’ LA CONFERMA ATTRAVERSO ESAME E L’APPORTO DI EVIDENZA OGGETTIVA CHE I REQUISITI PARTICOLARI PER L’UTILIZZAZIONE PREVISTA DEL METODO SIANO SODDISFATTI La validazione deve essere estesa in modo da soddisfare le esigenze di una data applicazione o di un campo di applicazione. Il laboratorio deve registrate i risultati ottenuti, le procedure utilizzate per la validazione, cosi pure una dichiarazione circa l’idoneità del metodo utilizzato.
 METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI VALIDAZIONE DEI METODI p.to 5.4.5 La validazione può comprendere procedure di campionamento, la manipolazione e il trasporto. Le tecniche utilizzate per la determinazione della prestazione di un metodo dovrebbero essere una, o una combinazione delle seguenti : 1) taratura, utilizzando campioni o materiali di riferimento 2) confronto dei risultati ottenuti con altri metodi 3) confronti interlaboratorio 4) valutazione sistematica dei fattori che influenzano il risultato 5) stima dell’incertezza dei risultati sulla base di una conoscenza scientifica dei principi teorici del metodo e di un’esperienza pratica. Quando sono effettuati dei cambiamenti nei metodi non normalizzati validati, l’influenza di tali cambiamenti dovrebbe essere documentata, e se necessario, dovrebbe essere eseguita una nuova validazione.
METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI VALIDAZIONE DEI METODI p.to 5.4.5 La validazione può comprendere procedure di campionamento, la manipolazione e il trasporto. Le tecniche utilizzate per la determinazione della prestazione di un metodo dovrebbero essere una, o una combinazione delle seguenti : 1) taratura, utilizzando campioni o materiali di riferimento 2) confronto dei risultati ottenuti con altri metodi 3) confronti interlaboratorio 4) valutazione sistematica dei fattori che influenzano il risultato 5) stima dell’incertezza dei risultati sulla base di una conoscenza scientifica dei principi teorici del metodo e di un’esperienza pratica. Quando sono effettuati dei cambiamenti nei metodi non normalizzati validati, l’influenza di tali cambiamenti dovrebbe essere documentata, e se necessario, dovrebbe essere eseguita una nuova validazione.
 METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI STIMA DELL’INCERTEZZA DI MISURA p.to 5.4.6 Un laboratorio di taratura o un laboratorio di prova che esegue le proprie tarature, deve avere e deve applicare una procedura per stimare l’incertezza di misura per tutte le tarature e tipi di taratura. I laboratori di prova devono avere e devono applicare procedure per stimare l’incertezza delle misure. In certi casi la natura dei metodi di prova può escludere il calcolo dell’incertezza di misura rigoroso e valido dal punto di vista metrologico e statistico. In questi casi il laboratorio deve almeno tentare di identificare tutte le componenti dell’incertezza e fare una stima ragionevole, e deve garantire che l’espressione del risultato non fornisca un’impressione errata dell’incertezza. Una stima ragionevole deve essere basata sulla conoscenza del metodo e sullo scopo della misura e deve fare uso, per esempio, delle esperienze precedenti e della validazione dei dati.
METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI STIMA DELL’INCERTEZZA DI MISURA p.to 5.4.6 Un laboratorio di taratura o un laboratorio di prova che esegue le proprie tarature, deve avere e deve applicare una procedura per stimare l’incertezza di misura per tutte le tarature e tipi di taratura. I laboratori di prova devono avere e devono applicare procedure per stimare l’incertezza delle misure. In certi casi la natura dei metodi di prova può escludere il calcolo dell’incertezza di misura rigoroso e valido dal punto di vista metrologico e statistico. In questi casi il laboratorio deve almeno tentare di identificare tutte le componenti dell’incertezza e fare una stima ragionevole, e deve garantire che l’espressione del risultato non fornisca un’impressione errata dell’incertezza. Una stima ragionevole deve essere basata sulla conoscenza del metodo e sullo scopo della misura e deve fare uso, per esempio, delle esperienze precedenti e della validazione dei dati.
 METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI STIMA DELL’INCERTEZZA DI MISURA p.to 5.4.6 Il livello di rigore necessario in una stima dell’incertezza di misura dipende da fattori come : - i requisiti del metodo di prova - i requisiti del cliente - l’esistenza di limiti stretti su cui sono basate le decisioni della conformità ad una specifica o ad una disposizione di legge. Nei casi un cui un , metodo di prova ben conosciuto specifica i limiti delle maggiori sorgenti di incertezza e specifica la forma di presentazione dei risultati calcolati, si ritiene che il laboratorio abbia soddisfatto questo punto , seguendo i metodi di prova e le istruzioni per la presentazione dei risultati.
METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI STIMA DELL’INCERTEZZA DI MISURA p.to 5.4.6 Il livello di rigore necessario in una stima dell’incertezza di misura dipende da fattori come : - i requisiti del metodo di prova - i requisiti del cliente - l’esistenza di limiti stretti su cui sono basate le decisioni della conformità ad una specifica o ad una disposizione di legge. Nei casi un cui un , metodo di prova ben conosciuto specifica i limiti delle maggiori sorgenti di incertezza e specifica la forma di presentazione dei risultati calcolati, si ritiene che il laboratorio abbia soddisfatto questo punto , seguendo i metodi di prova e le istruzioni per la presentazione dei risultati.
 METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI STIMA DELL’INCERTEZZA DI MISURA p.to 5.4.6 Le fonti che contribuiscono all’incertezza di misura includono, in modo non esaustivo: - i campioni di riferimento e i materiali di riferimento utilizzati, - i metodi e le apparecchiature utilizzate, - le condizioni ambientali, - le condizioni degli oggetti da provare o da tarare, - l’operatore. Il comportamento previsto a lungo termine dell’oggetto sottoposto a prova e/o taratura non è, di regola, preso in considerazione quanto si stima l’incertezza di misura. Per ulteriori informazioni sull’incertezza di misura vedere tra l’altro : - La norma ISO 5725 - parti 1/2/3/4/6 - La norma italiana sperimentale UNI CEI ENV 13005 :2000 “Guida all’espressione dell’incertezza di misura “ - Documenti dell’organismo di accreditamento ( es. DT -0002 SINAL) “ Guida per la dichiarazione dell’incertezza di misura”. Quando si stima l’incertezza di misura, devono essere prese in considerazione, utilizzando appropriati metodi di analisi, tutte le componenti dell’incertezza che sono di rilievo in una data situazione.
METODI DI PROVA E DI TARATURA E VALIDAZIONE DEI METODI STIMA DELL’INCERTEZZA DI MISURA p.to 5.4.6 Le fonti che contribuiscono all’incertezza di misura includono, in modo non esaustivo: - i campioni di riferimento e i materiali di riferimento utilizzati, - i metodi e le apparecchiature utilizzate, - le condizioni ambientali, - le condizioni degli oggetti da provare o da tarare, - l’operatore. Il comportamento previsto a lungo termine dell’oggetto sottoposto a prova e/o taratura non è, di regola, preso in considerazione quanto si stima l’incertezza di misura. Per ulteriori informazioni sull’incertezza di misura vedere tra l’altro : - La norma ISO 5725 - parti 1/2/3/4/6 - La norma italiana sperimentale UNI CEI ENV 13005 :2000 “Guida all’espressione dell’incertezza di misura “ - Documenti dell’organismo di accreditamento ( es. DT -0002 SINAL) “ Guida per la dichiarazione dell’incertezza di misura”. Quando si stima l’incertezza di misura, devono essere prese in considerazione, utilizzando appropriati metodi di analisi, tutte le componenti dell’incertezza che sono di rilievo in una data situazione.
 5.4.5 Validazione dei metodi 5.4.5.1 La validazione è la conferma attraverso esame e l’apporto di evidenza oggettiva che i requisiti particolari per l’utilizzazione prevista siano soddisfatti. 5.4.5.2 Il laboratorio deve validare i metodi normalizzati, i metodi sviluppati/progettati dal laboratorio, i metodi normalizzati utilizzati al di fuori del proprio scopo e campo di applicazione prefissato, come pure estensioni e modifiche di metodi normalizzati per confermare che i metodi siano adatti all’utilizzazione prevista. La validazione deve essere estesa in modo da soddisfare le esigenze di una data applicazione o di un campo di applicazione. Il laboratorio deve registrare i risultati ottenuti, le procedure utilizzate per la validazione, così pure una dichiarazione circa l’idoneità del metodo per l’utilizzo previsto.
5.4.5 Validazione dei metodi 5.4.5.1 La validazione è la conferma attraverso esame e l’apporto di evidenza oggettiva che i requisiti particolari per l’utilizzazione prevista siano soddisfatti. 5.4.5.2 Il laboratorio deve validare i metodi normalizzati, i metodi sviluppati/progettati dal laboratorio, i metodi normalizzati utilizzati al di fuori del proprio scopo e campo di applicazione prefissato, come pure estensioni e modifiche di metodi normalizzati per confermare che i metodi siano adatti all’utilizzazione prevista. La validazione deve essere estesa in modo da soddisfare le esigenze di una data applicazione o di un campo di applicazione. Il laboratorio deve registrare i risultati ottenuti, le procedure utilizzate per la validazione, così pure una dichiarazione circa l’idoneità del metodo per l’utilizzo previsto.
 NOTA 1: La validazione può comprendere procedure per il campionamento, la manipolazione e il trasporto. NOTA 2: Le tecniche utilizzate per la determinazione della prestazione di un metodo dovrebbero essere una, o una combinazione delle seguenti: taratura, utilizzando campioni o materiali di riferimento; confronto dei risultati ottenuti con altri metodi; confronti interlaboratorio; valutazione sistematica dei fattori che influenzano il risultato; stima dell’incertezza dei risultati sulla base della conoscenza scientifica dei principi teorici del metodo e dell’esperienza pratica. NOTA 3: Quando sono effettuati dei cambiamenti nei metodi non normalizzati validati, l’influenza di tali cambiamenti dovrebbe essere documentata, e se necessario, dovrebbe essere eseguita una nuova validazione.
NOTA 1: La validazione può comprendere procedure per il campionamento, la manipolazione e il trasporto. NOTA 2: Le tecniche utilizzate per la determinazione della prestazione di un metodo dovrebbero essere una, o una combinazione delle seguenti: taratura, utilizzando campioni o materiali di riferimento; confronto dei risultati ottenuti con altri metodi; confronti interlaboratorio; valutazione sistematica dei fattori che influenzano il risultato; stima dell’incertezza dei risultati sulla base della conoscenza scientifica dei principi teorici del metodo e dell’esperienza pratica. NOTA 3: Quando sono effettuati dei cambiamenti nei metodi non normalizzati validati, l’influenza di tali cambiamenti dovrebbe essere documentata, e se necessario, dovrebbe essere eseguita una nuova validazione.
 5.4.5.3 Il campo e l'accuratezza dei valori ottenibili da metodi validati (per esempio l'incertezza dei risultati, i limiti di rilevazione, la selettività del metodo, la linearità, la ripetibilità e/o la riproducibilità, la robustezza nei confronti di influenze esterne e/o la sensibilità incrociata nei confronti di interferenze provenienti dalla matrice del campione/oggetto da provare), così come valutati per l'utilizzo previsto, devono corrispondere alle esigenze del cliente. Nota 1: La validazione comprende la specifica dei requisiti, la determinazione delle caratteristiche dei metodi, un controllo che i requisiti possano essere soddisfatti utilizzando il metodo e una dichiarazione relativa alla validità. Nota 2: In funzione dello sviluppo del metodo, dovrebbero essere eseguiti riesami regolari per verificare che le esigenze del cliente continuino ad essere soddisfatte. Qualsiasi variazione dei requisiti che richieda modifiche al piano di sviluppo dovrebbe essere approvata e autorizzata. Nota 3: La validazione è sempre un bilancio fra i costi, i rischi e le possibilità tecniche. Vi sono molti casi in cui il campo e l'incertezza dei valori (per esempio l‘accuratezza, i limiti di rilevazione, la selettività, la linearità, la ripetibilità e la riproducibilità, la robustezza e/o la sensibilità alle interferenze) possono essere solo forniti in modo semplificato a causa di mancanza di informazioni. (dalla UNI CEI EN ISO/IEC 17025)
5.4.5.3 Il campo e l'accuratezza dei valori ottenibili da metodi validati (per esempio l'incertezza dei risultati, i limiti di rilevazione, la selettività del metodo, la linearità, la ripetibilità e/o la riproducibilità, la robustezza nei confronti di influenze esterne e/o la sensibilità incrociata nei confronti di interferenze provenienti dalla matrice del campione/oggetto da provare), così come valutati per l'utilizzo previsto, devono corrispondere alle esigenze del cliente. Nota 1: La validazione comprende la specifica dei requisiti, la determinazione delle caratteristiche dei metodi, un controllo che i requisiti possano essere soddisfatti utilizzando il metodo e una dichiarazione relativa alla validità. Nota 2: In funzione dello sviluppo del metodo, dovrebbero essere eseguiti riesami regolari per verificare che le esigenze del cliente continuino ad essere soddisfatte. Qualsiasi variazione dei requisiti che richieda modifiche al piano di sviluppo dovrebbe essere approvata e autorizzata. Nota 3: La validazione è sempre un bilancio fra i costi, i rischi e le possibilità tecniche. Vi sono molti casi in cui il campo e l'incertezza dei valori (per esempio l‘accuratezza, i limiti di rilevazione, la selettività, la linearità, la ripetibilità e la riproducibilità, la robustezza e/o la sensibilità alle interferenze) possono essere solo forniti in modo semplificato a causa di mancanza di informazioni. (dalla UNI CEI EN ISO/IEC 17025)
 Esempi di situazioni sperimentali richiedenti la validazione: un nuovo metodo è sviluppato per scopi particolari; un metodo analitico stabilito deve essere aggiornato, migliorato o esteso ad un nuovo problema analitico; il controllo di qualità evidenzia variazioni temporali dei parametri di qualità; un metodo stabilito deve essere usato in un diverso laboratorio, da un diverso analista, con diversa strumentazione; è necessario dimostrare l’equivalenza del metodo in esame con un metodo standard.
Esempi di situazioni sperimentali richiedenti la validazione: un nuovo metodo è sviluppato per scopi particolari; un metodo analitico stabilito deve essere aggiornato, migliorato o esteso ad un nuovo problema analitico; il controllo di qualità evidenzia variazioni temporali dei parametri di qualità; un metodo stabilito deve essere usato in un diverso laboratorio, da un diverso analista, con diversa strumentazione; è necessario dimostrare l’equivalenza del metodo in esame con un metodo standard.

 Le procedure di validazione dipendono dal tipo di analisi da eseguire. Parametri di interesse nelle procedure di validazione analisi analisi di metodi di: qualitativa quantitativa Accuratezza (esattezza e precisione) - Range dinamico e lineare - Selettività/specificità Limite di rivelabilità Limite di quantificazione - Robustezza Recupero -
Le procedure di validazione dipendono dal tipo di analisi da eseguire. Parametri di interesse nelle procedure di validazione analisi analisi di metodi di: qualitativa quantitativa Accuratezza (esattezza e precisione) - Range dinamico e lineare - Selettività/specificità Limite di rivelabilità Limite di quantificazione - Robustezza Recupero -
 13 В последнее десятилетие почти все официальные методы для анализа пищевых продуктов в разделе “Точные науки (Precision)“ начинаются одним из следующих предложений: “Повторяемость (r): Разница между двумя отдельными результатами обнаруживается на идентично анализируемом материале одним специалистом, с использованием одного и того же оборудования за один короткий промежуток времени не превышающий 2,0% от среднеарифметического результата.“
13 В последнее десятилетие почти все официальные методы для анализа пищевых продуктов в разделе “Точные науки (Precision)“ начинаются одним из следующих предложений: “Повторяемость (r): Разница между двумя отдельными результатами обнаруживается на идентично анализируемом материале одним специалистом, с использованием одного и того же оборудования за один короткий промежуток времени не превышающий 2,0% от среднеарифметического результата.“
 14 или “Повторяемость(r): Разница между двумя измерениями, выполняемыми одновременно или в быстрой последовательности одним специалистом, не должна превышать 0,6 гр. масла на 100г. образца. “ или “Повторяемость(r): Разница между результатами двух исследований, выполняемых одновременно или в быстрой последовательности одним специалистом на одном аппарате, не должна превышать 6% относительно средне арифметического из результатов как для калия, так и для натрия.“
14 или “Повторяемость(r): Разница между двумя измерениями, выполняемыми одновременно или в быстрой последовательности одним специалистом, не должна превышать 0,6 гр. масла на 100г. образца. “ или “Повторяемость(r): Разница между результатами двух исследований, выполняемых одновременно или в быстрой последовательности одним специалистом на одном аппарате, не должна превышать 6% относительно средне арифметического из результатов как для калия, так и для натрия.“
 15 ЧЕТКОСТЬ (ACCURACY) Четкость аналитического метода описывает близость средних результатов испытаний, полученных методом к истинному значению (концентрации) аналита. Четкость определяется повтором анализа проб, содержащих известное количество аналита. Четкость должна быть измерена с помощью минимум 5 исследований концентраций. И к исследованиям рекомендованы минимум 3 концентрации в ожидаемых диапазонах.
15 ЧЕТКОСТЬ (ACCURACY) Четкость аналитического метода описывает близость средних результатов испытаний, полученных методом к истинному значению (концентрации) аналита. Четкость определяется повтором анализа проб, содержащих известное количество аналита. Четкость должна быть измерена с помощью минимум 5 исследований концентраций. И к исследованиям рекомендованы минимум 3 концентрации в ожидаемых диапазонах.
 16 ТОЧНОСТЬ (PRECISION) Точность аналитического метода характеризуется близостью отдельных методов аналита, когда процедура применяется не однократно на несколько aliquots одного однородного объема биологической матрицы. Точность должна быть измерена с помощью минимум 5 определений в концентрации. Рекомендуется исследование минимум 3 концентраций в ожидаемых диапазонах.
16 ТОЧНОСТЬ (PRECISION) Точность аналитического метода характеризуется близостью отдельных методов аналита, когда процедура применяется не однократно на несколько aliquots одного однородного объема биологической матрицы. Точность должна быть измерена с помощью минимум 5 определений в концентрации. Рекомендуется исследование минимум 3 концентраций в ожидаемых диапазонах.
 17 ТОЧНОСТЬ Точность далее подразделяется на: повторяемость или перспектива (into within-run), точность внутри партии, которая оценивается во время одного исследования, и между сериями исследований проведенных одним специалистом в одной лаборатории воспроизводимость или точность среди партий, которые могут измеряться во времени, и могут быть измерены разными специалистами, оборудованием, реагентами и лабораториями.
17 ТОЧНОСТЬ Точность далее подразделяется на: повторяемость или перспектива (into within-run), точность внутри партии, которая оценивается во время одного исследования, и между сериями исследований проведенных одним специалистом в одной лаборатории воспроизводимость или точность среди партий, которые могут измеряться во времени, и могут быть измерены разными специалистами, оборудованием, реагентами и лабораториями.
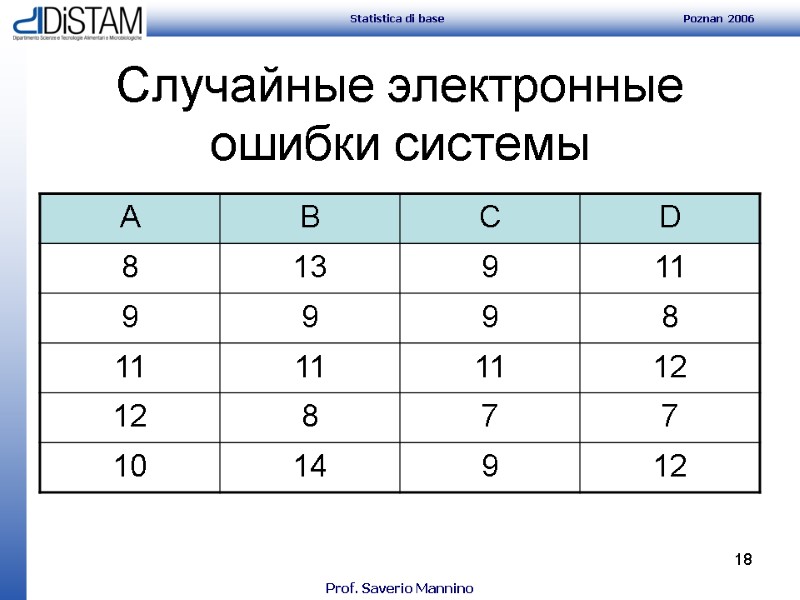
 18 Случайные электронные ошибки системы
18 Случайные электронные ошибки системы
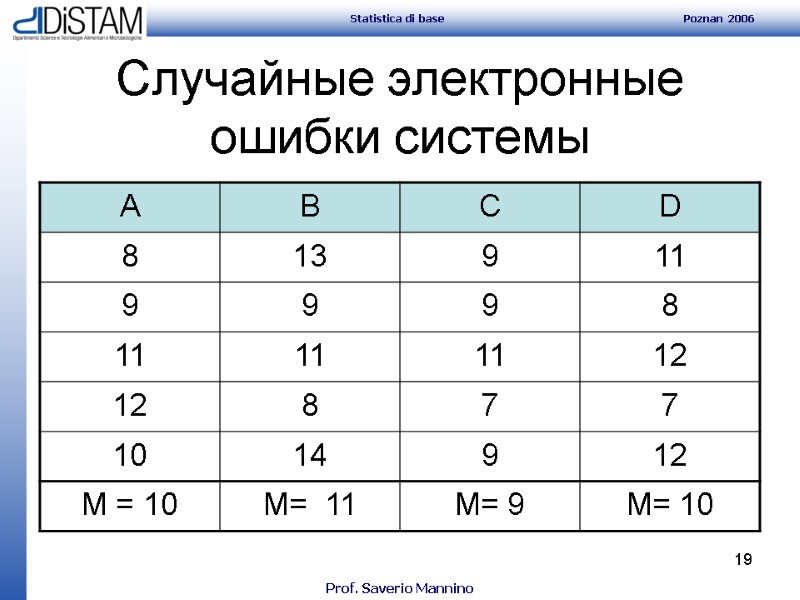
 19 Случайные электронные ошибки системы
19 Случайные электронные ошибки системы
 20 Случайные электронные ошибки системы
20 Случайные электронные ошибки системы
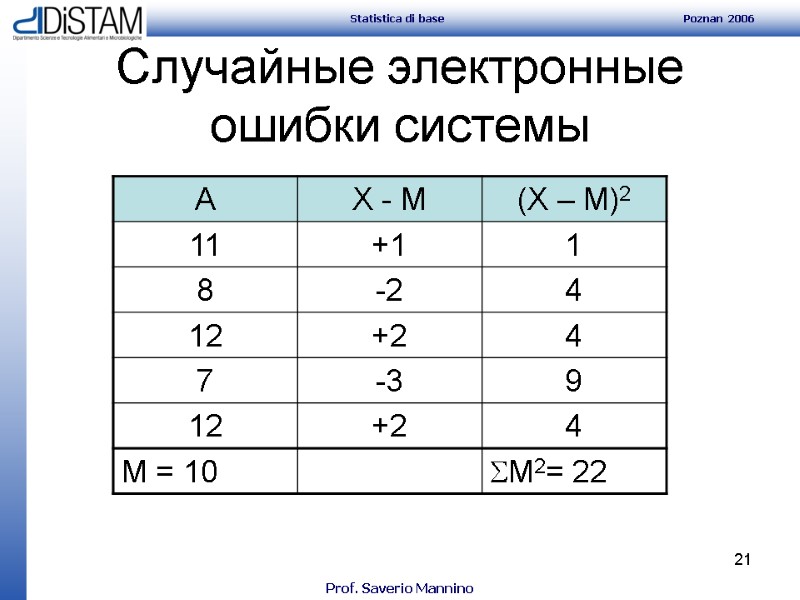
 21 Случайные электронные ошибки системы
21 Случайные электронные ошибки системы
 22 Случайные электронные ошибки системы
22 Случайные электронные ошибки системы
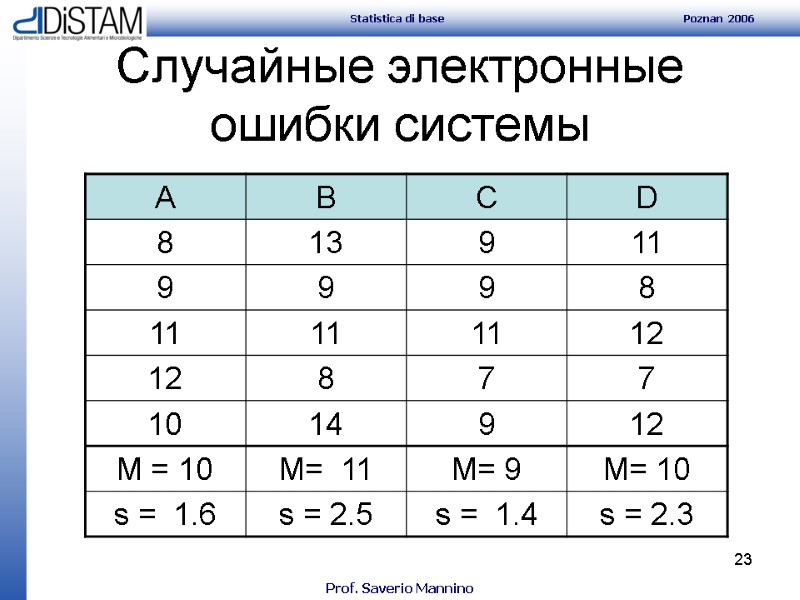
 23 Случайные электронные ошибки системы
23 Случайные электронные ошибки системы
 24 Средние и стандартные отклонения Среднее Расхождение Стандартное отклонение
24 Средние и стандартные отклонения Среднее Расхождение Стандартное отклонение
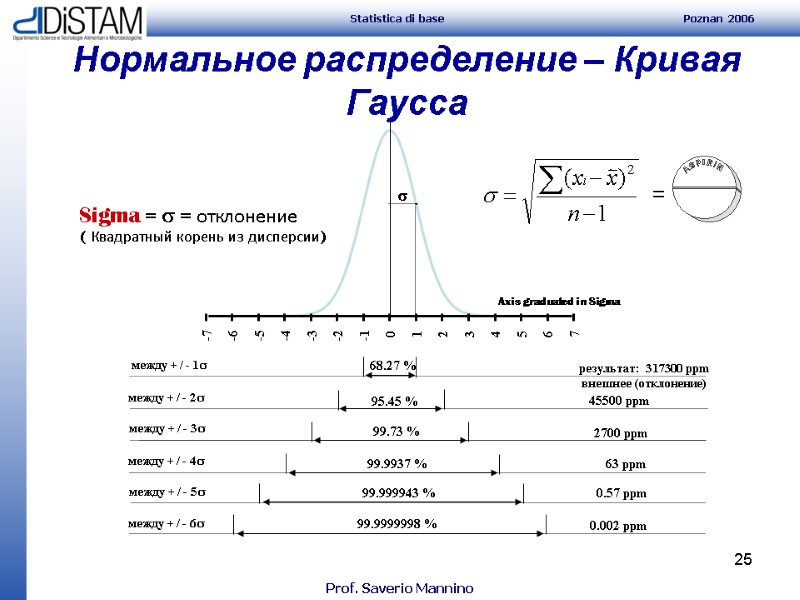
 25 Sigma = = отклонение ( Квадратный корень из дисперсии) Axis graduated in Sigma 68.27 % 95.45 % 99.73 % 99.9937 % 99.999943 % 99.9999998 % результат: 317300 ppm внешнее (отклонение) 45500 ppm 2700 ppm 63 ppm 0.57 ppm 0.002 ppm между + / - 1 между + / - 2 между + / - 3 между + / - 4 между + / - 5 между + / - 6 = Нормальное распределение – Кривая Гаусса
25 Sigma = = отклонение ( Квадратный корень из дисперсии) Axis graduated in Sigma 68.27 % 95.45 % 99.73 % 99.9937 % 99.999943 % 99.9999998 % результат: 317300 ppm внешнее (отклонение) 45500 ppm 2700 ppm 63 ppm 0.57 ppm 0.002 ppm между + / - 1 между + / - 2 между + / - 3 между + / - 4 между + / - 5 между + / - 6 = Нормальное распределение – Кривая Гаусса
 26 Пример расчета точных данных Образец был проанализирован 5 раз и мы хотим вычислить SD (стандартное отклонение)
26 Пример расчета точных данных Образец был проанализирован 5 раз и мы хотим вычислить SD (стандартное отклонение)
 27 Точность и четкость Соотношение точности и четкости можно проиллюстрировать известным примером стрельбы из винтовки по мишеням, где черные точки ниже представляют просмотр целей. Вы можете видеть, что хорошая прицельность не обязательно даст точное попадание. Однако, если инструмент хорошо прилажен, четкость и воспроизводимость результата является хорошей мерой точности.
27 Точность и четкость Соотношение точности и четкости можно проиллюстрировать известным примером стрельбы из винтовки по мишеням, где черные точки ниже представляют просмотр целей. Вы можете видеть, что хорошая прицельность не обязательно даст точное попадание. Однако, если инструмент хорошо прилажен, четкость и воспроизводимость результата является хорошей мерой точности.
 28
28
 29
29
 30 Доверительный интервал Пример: Расчет доверительного интервала (или лимита) в среднем на уровне вероятности 80, 95 e 99% при следующем наборе данных: 47.64; 47.69; 47.52; 47.55 M= 47.60 s= 0.08 = n-1= 4-1= 3
30 Доверительный интервал Пример: Расчет доверительного интервала (или лимита) в среднем на уровне вероятности 80, 95 e 99% при следующем наборе данных: 47.64; 47.69; 47.52; 47.55 M= 47.60 s= 0.08 = n-1= 4-1= 3
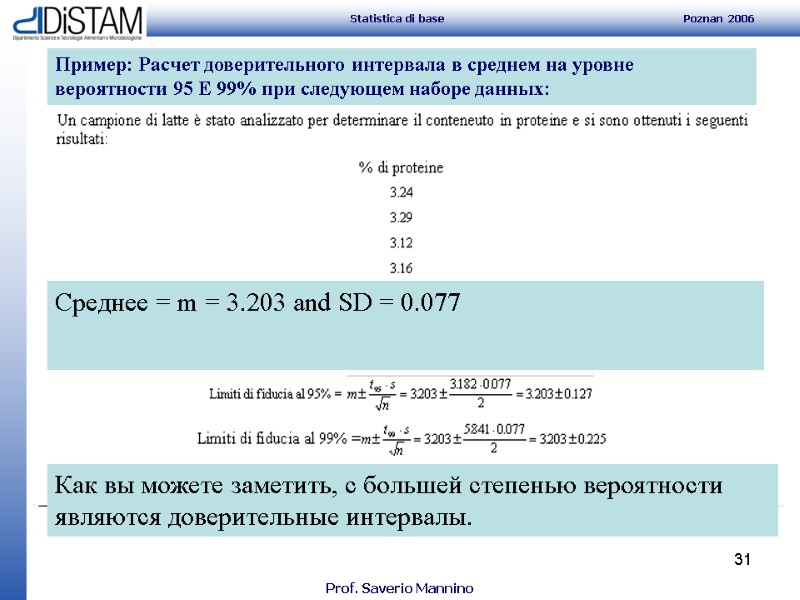
 31 Пример: Расчет доверительного интервала в среднем на уровне вероятности 95 E 99% при следующем наборе данных: Среднее = m = 3.203 and SD = 0.077 Как вы можете заметить, с большей степенью вероятности являются доверительные интервалы.
31 Пример: Расчет доверительного интервала в среднем на уровне вероятности 95 E 99% при следующем наборе данных: Среднее = m = 3.203 and SD = 0.077 Как вы можете заметить, с большей степенью вероятности являются доверительные интервалы.
 32 РАСЧЕТ СТАНДАРТНОГО ОТКЛОНЕНИЯ (SD) Пример 1ый: SD рассчитывается из серии дубликатов анализов из одного образца Пример 2ой: SD рассчитывается из серии дубликатов анализов из разных, но похожих образцов d = дубликаты K = количество дубликатов
32 РАСЧЕТ СТАНДАРТНОГО ОТКЛОНЕНИЯ (SD) Пример 1ый: SD рассчитывается из серии дубликатов анализов из одного образца Пример 2ой: SD рассчитывается из серии дубликатов анализов из разных, но похожих образцов d = дубликаты K = количество дубликатов
 33 Пример 1 7 продублированных анализов из одного образца
33 Пример 1 7 продублированных анализов из одного образца
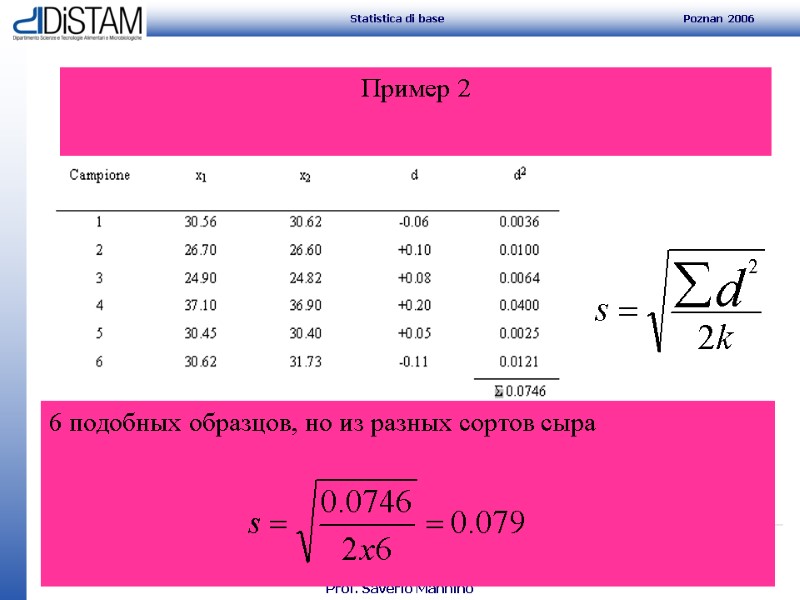
 34 Пример 2 6 подобных образцов, но из разных сортов сыра
34 Пример 2 6 подобных образцов, но из разных сортов сыра
 35 Факторы стандартного отклонения (SD) от диапазона For n=2
35 Факторы стандартного отклонения (SD) от диапазона For n=2
 36 или “Повторяемость (r): Разница между двумя измерениями, выполняемыми одновременно или в быстрой последовательности одним специалистом не должна превышать 0.6 гр. масла на 100 гр. образца. “ или “Повторяемость (r): разница между двумя результатами двух исследований, выполненных одновременно или в быстрой последовательности одним специалистом используя один аппарат, не должна превышать 6% относительно среднего арифметического результата и для натрия и для калия. “
36 или “Повторяемость (r): Разница между двумя измерениями, выполняемыми одновременно или в быстрой последовательности одним специалистом не должна превышать 0.6 гр. масла на 100 гр. образца. “ или “Повторяемость (r): разница между двумя результатами двух исследований, выполненных одновременно или в быстрой последовательности одним специалистом используя один аппарат, не должна превышать 6% относительно среднего арифметического результата и для натрия и для калия. “
 37 Предел повторяемости Предел повторяемости: t - это t-Student (2 фракции) для = и в 95% случаев вероятности это t = 1,96 2. r – повторяемость стандартного отклонения. r – максимальное значение, которое можно спрогнозировать для различий двух результатов, полученных в условиях повторяемости.
37 Предел повторяемости Предел повторяемости: t - это t-Student (2 фракции) для = и в 95% случаев вероятности это t = 1,96 2. r – повторяемость стандартного отклонения. r – максимальное значение, которое можно спрогнозировать для различий двух результатов, полученных в условиях повторяемости.
 38 Предел повторяемости Это исходит из формулы, что позволяет рассчитать стандартное отклонение от двойных измерений Где n= 1
38 Предел повторяемости Это исходит из формулы, что позволяет рассчитать стандартное отклонение от двойных измерений Где n= 1
 39 Предел повторяемости Предел повторяемости: То же, что и раньше, но в условиях воспроизводимости
39 Предел повторяемости Предел повторяемости: То же, что и раньше, но в условиях воспроизводимости
 40
40
 41 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Часто, мы должны принять решение о видах популяции, на основе данных полученных из образцов. Пример: Нам нужно знать, какая партия лучше другой или который поставщик лучший. Для достижения результата необходимо начать с предположений о двух видах популяции. Такое предположение называется статистической гипотезой. Процедуры, приводящие к установлению истины или ложности гипотезы статистический тест или тест значимости или испытание гипотезы.
41 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Часто, мы должны принять решение о видах популяции, на основе данных полученных из образцов. Пример: Нам нужно знать, какая партия лучше другой или который поставщик лучший. Для достижения результата необходимо начать с предположений о двух видах популяции. Такое предположение называется статистической гипотезой. Процедуры, приводящие к установлению истины или ложности гипотезы статистический тест или тест значимости или испытание гипотезы.
 42 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Проверяемые гипотезы, обозначаются H0, называются Нулевая Гипотеза, потому что это означает, что на самом деле нет реальной разницы между истинным значением параметров популяции и его предположением о ценности образца. Пример: Если мы желаем определить когда один процесс лучше другого, мы создаем гипотезу что нет разницу между двумя процессами. Любая гипотеза, которая отличается от Нулевой Гипотезы обозначается H1 и называется Альтернативной Гипотезой
42 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Проверяемые гипотезы, обозначаются H0, называются Нулевая Гипотеза, потому что это означает, что на самом деле нет реальной разницы между истинным значением параметров популяции и его предположением о ценности образца. Пример: Если мы желаем определить когда один процесс лучше другого, мы создаем гипотезу что нет разницу между двумя процессами. Любая гипотеза, которая отличается от Нулевой Гипотезы обозначается H1 и называется Альтернативной Гипотезой
 43 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ При проверке статистических гипотез нет абсолютной уверенности, что выводы будут правильными. На 5% отметке (уровне), мы можем быть не правы 1 к 20 (или 5 к 100) и на уровне 1% - 1 к 100. α значение
43 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ При проверке статистических гипотез нет абсолютной уверенности, что выводы будут правильными. На 5% отметке (уровне), мы можем быть не правы 1 к 20 (или 5 к 100) и на уровне 1% - 1 к 100. α значение
 44 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Возможны два вида не верных выводов. Если гипотеза верна и выбранный образец говорит об ошибке, мы говорим, что мы совершили Тип ошибки №1 или ошибку α Если окажется, что гипотеза проходящая испытание на самом деле ошибочна, и образец это подтверждает, мы говорим, что был совершен Тип ошибки №2. ( или ошибка β)
44 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Возможны два вида не верных выводов. Если гипотеза верна и выбранный образец говорит об ошибке, мы говорим, что мы совершили Тип ошибки №1 или ошибку α Если окажется, что гипотеза проходящая испытание на самом деле ошибочна, и образец это подтверждает, мы говорим, что был совершен Тип ошибки №2. ( или ошибка β)
 45 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Реальные ситуации H0 правильная H0 ошибочная H0 правильная Результаты испытаний H0 ошибочная Есть 4 варианта результатов испытаний α -риск производителя и β – риск потребителя
45 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Реальные ситуации H0 правильная H0 ошибочная H0 правильная Результаты испытаний H0 ошибочная Есть 4 варианта результатов испытаний α -риск производителя и β – риск потребителя
 46 Тест F F-тест используется для определения, существенно ли различаются две дисперсии. F объем определяется следующим соотношением: F = sa2 / sb2 где sa2 = это дисперсия популяции «А» оценивается с помощью na-1 degree of freedom sb2 = это дисперсия популяции «B» оценивается с помощью na-1 degree of freedom sa2 – большая дисперсия
46 Тест F F-тест используется для определения, существенно ли различаются две дисперсии. F объем определяется следующим соотношением: F = sa2 / sb2 где sa2 = это дисперсия популяции «А» оценивается с помощью na-1 degree of freedom sb2 = это дисперсия популяции «B» оценивается с помощью na-1 degree of freedom sa2 – большая дисперсия
 47 Расчет значения F сравнивается с отчетом в F-таблице . При выполнении F-теста мы предполагаем, что дисперсия обоих популяций и «A» и «B» одинаковы. Таким образом Нулевая гипотеза: H0 : A = B E и альтернативная гипотеза, что дисперсии различны: H1 : A B Если значение F имеет меньший показатель расчета чем табличный вариант, мы предполагаем что нет разницы между двумя дисперсиями, таким образом верна Альтернативная гипотеза. Тест F
47 Расчет значения F сравнивается с отчетом в F-таблице . При выполнении F-теста мы предполагаем, что дисперсия обоих популяций и «A» и «B» одинаковы. Таким образом Нулевая гипотеза: H0 : A = B E и альтернативная гипотеза, что дисперсии различны: H1 : A B Если значение F имеет меньший показатель расчета чем табличный вариант, мы предполагаем что нет разницы между двумя дисперсиями, таким образом верна Альтернативная гипотеза. Тест F
 48 T-тест В аналитической практике часто встречается необходимость сопоставить два средства с целью найти в них разницу. В таком случае может быть использован t-тест. Процедура Сформулируйте нулевую гипотезу Выберите доверительный уровень (p = 0.05) Вычислите t от данных Сравните t с табличным вариантом Если t-величина вычисленная из данных ниже чем табличные данные мы можем заявить, что там нет существенной разницы между двумя средствами.
48 T-тест В аналитической практике часто встречается необходимость сопоставить два средства с целью найти в них разницу. В таком случае может быть использован t-тест. Процедура Сформулируйте нулевую гипотезу Выберите доверительный уровень (p = 0.05) Вычислите t от данных Сравните t с табличным вариантом Если t-величина вычисленная из данных ниже чем табличные данные мы можем заявить, что там нет существенной разницы между двумя средствами.
 49 Примеры Компания производит замороженные креветки с отметкой на упаковке “Каждая 12 унций”. Образцы из четырех пакетов выбранные случайным образом показали следующий вес: 12.2; 11.6; 11.8; 11.6 На уровне 5%, это означает, что образцы значительно отличаются от отметки на упаковке?
49 Примеры Компания производит замороженные креветки с отметкой на упаковке “Каждая 12 унций”. Образцы из четырех пакетов выбранные случайным образом показали следующий вес: 12.2; 11.6; 11.8; 11.6 На уровне 5%, это означает, что образцы значительно отличаются от отметки на упаковке?
 50 Пример Среднее значение= 47.2/4 = 11.8 s = 0.282 tвычисленная = 1.41 tтабличная = 3.18 for 3 degree of freedom Если tтабличная больше чем tвычисленная значит нет значительной разницы между M и X
50 Пример Среднее значение= 47.2/4 = 11.8 s = 0.282 tвычисленная = 1.41 tтабличная = 3.18 for 3 degree of freedom Если tтабличная больше чем tвычисленная значит нет значительной разницы между M и X
 51 Примеры Новые микропипетки предполагают дозировать 20,0 µl. Чтобы проверить 5 исследований использовались аналитические весы. Вот результаты: 19.6 - 19.4 - 20.1- 19.9 – 19.5 На 5% уровне, это означает, что образцы значительно отличаются от отметки на упаковке? НЕТ……. ПОЧЕМУ
51 Примеры Новые микропипетки предполагают дозировать 20,0 µl. Чтобы проверить 5 исследований использовались аналитические весы. Вот результаты: 19.6 - 19.4 - 20.1- 19.9 – 19.5 На 5% уровне, это означает, что образцы значительно отличаются от отметки на упаковке? НЕТ……. ПОЧЕМУ
 52 Примеры M= 19.7 s= 0.291 t вычисленная = 2.3 t вычисленная = 2.776 for 5 degree of freedom Если tтабличная больше чем tвычисленная значит нет значительной разницы между M и X
52 Примеры M= 19.7 s= 0.291 t вычисленная = 2.3 t вычисленная = 2.776 for 5 degree of freedom Если tтабличная больше чем tвычисленная значит нет значительной разницы между M и X
 53 Примеры M= 19.7 s= 0.291 X = 20 t вычисленная = 2.3 tвычисленная = 2.776 for 5 degree of freedom Значение знаменателя 0.130 и это стандартная ошибка среднего значения. Это означает, что наш результат можно представить в виде: µ = 19.7 ± 2.776 (0.13) Начиная с 19.34 до 20.06 И 20 в этом интервале
53 Примеры M= 19.7 s= 0.291 X = 20 t вычисленная = 2.3 tвычисленная = 2.776 for 5 degree of freedom Значение знаменателя 0.130 и это стандартная ошибка среднего значения. Это означает, что наш результат можно представить в виде: µ = 19.7 ± 2.776 (0.13) Начиная с 19.34 до 20.06 И 20 в этом интервале
 54
54
 55 Парные Т тесты Мы проанализировали образец двумя методами и его результаты представлены ниже. Нам нужно знать, дают ли два разных метода одинаковый результат.
55 Парные Т тесты Мы проанализировали образец двумя методами и его результаты представлены ниже. Нам нужно знать, дают ли два разных метода одинаковый результат.
 56 Парный T тест Для начала вычислили разницу: Σ d = 3.2 и dсредний= 0.32 И затем возвели в квадрат разницу Σd2 = 1.94
56 Парный T тест Для начала вычислили разницу: Σ d = 3.2 и dсредний= 0.32 И затем возвели в квадрат разницу Σd2 = 1.94
 57 Парный T тест Σ d = 3.2 и dсредний = 0.32 Σd2 = 1.94 and df = 9 Гипотезы: H0 : a = b H1 : a ≠ b α = 0.05
57 Парный T тест Σ d = 3.2 и dсредний = 0.32 Σd2 = 1.94 and df = 9 Гипотезы: H0 : a = b H1 : a ≠ b α = 0.05
 58 Парный T тест t из таблицы на 9 degree of freedom is : t = 2.26 Being 3.172 > 2.26 Мы можем заключить что два метода в 95% случаев дают разные результаты
58 Парный T тест t из таблицы на 9 degree of freedom is : t = 2.26 Being 3.172 > 2.26 Мы можем заключить что два метода в 95% случаев дают разные результаты
 59 ТОЧНОСТЬ Точность аналитического метода описывает близость средних данных результатов полученных методом к истинному значению (концентрации) аналита. Точность определяется повтором анализа проб, содержащие известное количество аналита. Точность должна быть измерена не менее чем в 5 вычислениях концентрата. Рекомендуется исследование минимум 3 концентраций в ожидаемом диапазоне концентраций. Среднее значение должно быть в пределах 15% от фактического значения, кроме LLOQ, где оно не должно отклоняться более чем на 20%. Отклонение среднего от истинного значения служит мерой точности.
59 ТОЧНОСТЬ Точность аналитического метода описывает близость средних данных результатов полученных методом к истинному значению (концентрации) аналита. Точность определяется повтором анализа проб, содержащие известное количество аналита. Точность должна быть измерена не менее чем в 5 вычислениях концентрата. Рекомендуется исследование минимум 3 концентраций в ожидаемом диапазоне концентраций. Среднее значение должно быть в пределах 15% от фактического значения, кроме LLOQ, где оно не должно отклоняться более чем на 20%. Отклонение среднего от истинного значения служит мерой точности.
 60 ВОССТАНОВЛЕНИЕ Процент извлечения аналита из сложной матрицы - это отношение отклика детектора экстрагированного из сложной матрицы аналита, к отклику детектора подлинного образца аналита с истинной концентрацией. Восстановление относится к эффективности применения аналитического метода в пределах изменчивости. Восстановление аналита не должно быть на все 100%, но степень восстановления аналита и внутренний стандарт должен быть последовательным, точным и воспроизводимым. Эксперимент восстановления должен проводиться путем сравнения результатов анализа исследований трех концентратов (низкий, средний, высокий) со стандартом, который представляет 100% восстановление.
60 ВОССТАНОВЛЕНИЕ Процент извлечения аналита из сложной матрицы - это отношение отклика детектора экстрагированного из сложной матрицы аналита, к отклику детектора подлинного образца аналита с истинной концентрацией. Восстановление относится к эффективности применения аналитического метода в пределах изменчивости. Восстановление аналита не должно быть на все 100%, но степень восстановления аналита и внутренний стандарт должен быть последовательным, точным и воспроизводимым. Эксперимент восстановления должен проводиться путем сравнения результатов анализа исследований трех концентратов (низкий, средний, высокий) со стандартом, который представляет 100% восстановление.
 61 СЕЛЕКТИВНОСТЬ Селективность - это способность аналитического метода дифферинцировать и определять количество аналита в других компонентах образца. Для селективности, анализы чистого образца, соответствующие биологической матрице (плазма, моча или другие матрицы) должны быть получены как минимум из 6 источников. Каждый чистый образец должен быть протестирован на интерференции, и селективность должна быть проверена на нижнем уровне количественного анализа (LLOQ). Потенциальные вмешательства интерференций в биологические матрицы включая эндогенные компоненты матрицы, метаболиты, продукты распада, и при фактическом исследовании, сопутствующие препараты и другие внешние ксенобиотики. Если метод предназначен для определения более одного аналита, каждый аналит должен быть протестирован, чтобы гарантировать отсутствие интерференций.
61 СЕЛЕКТИВНОСТЬ Селективность - это способность аналитического метода дифферинцировать и определять количество аналита в других компонентах образца. Для селективности, анализы чистого образца, соответствующие биологической матрице (плазма, моча или другие матрицы) должны быть получены как минимум из 6 источников. Каждый чистый образец должен быть протестирован на интерференции, и селективность должна быть проверена на нижнем уровне количественного анализа (LLOQ). Потенциальные вмешательства интерференций в биологические матрицы включая эндогенные компоненты матрицы, метаболиты, продукты распада, и при фактическом исследовании, сопутствующие препараты и другие внешние ксенобиотики. Если метод предназначен для определения более одного аналита, каждый аналит должен быть протестирован, чтобы гарантировать отсутствие интерференций.
 62 Калибровка/Стандартная кривая Стандартная калибровочная кривая - это взаимосвязь между итогами анализа и известными концентрациями анализируемого. Стандартная кривая должна быть сделана для каждого вещества в образце. Должно быть использовано достаточное количество стандартов для надлежащего определения соотношения между концентрацией и анализом. Калибровочная кривая должна быть создана по той же биологической матрице, что и образец, предназначенный для создания пиков матрицы с известными концентрациями анализируемого. Сумма стандартов, используемых при строении калибровочной кривой, – это функция ожидаемого ряда аналитических величин и сущность анализируемого/итог соотношений.
62 Калибровка/Стандартная кривая Стандартная калибровочная кривая - это взаимосвязь между итогами анализа и известными концентрациями анализируемого. Стандартная кривая должна быть сделана для каждого вещества в образце. Должно быть использовано достаточное количество стандартов для надлежащего определения соотношения между концентрацией и анализом. Калибровочная кривая должна быть создана по той же биологической матрице, что и образец, предназначенный для создания пиков матрицы с известными концентрациями анализируемого. Сумма стандартов, используемых при строении калибровочной кривой, – это функция ожидаемого ряда аналитических величин и сущность анализируемого/итог соотношений.
 63 КАЛИБРОВОЧНАЯ КРИВАЯ Концентрации стандартов должны быть выбраны на основе концентраций, ожидаемых при исследованиях. Калибровочная кривая должна состоять из чистого образца (матрица образца обрабатывается без внутреннего стандарта), нулевого образца (матрица образца обрабатывается с учетом внутреннего стандарта), и от 6 до 8 не нулевых образцов диапазона ожидаемого покрытия, в том числе LLOQ.
63 КАЛИБРОВОЧНАЯ КРИВАЯ Концентрации стандартов должны быть выбраны на основе концентраций, ожидаемых при исследованиях. Калибровочная кривая должна состоять из чистого образца (матрица образца обрабатывается без внутреннего стандарта), нулевого образца (матрица образца обрабатывается с учетом внутреннего стандарта), и от 6 до 8 не нулевых образцов диапазона ожидаемого покрытия, в том числе LLOQ.
 64 1. Нижний предел количественного анализа (LLOQ) Самый низкий уровень кривой должен быть принят как стандарт квантификации, если соблюдены следующие условия: Реакция аналита на LLOQ должна быть проверена минимум в 5 случаях и сравнена с реакцией на чистую реакцию. Пик аналита (реакции) должен быть идентифицорованым, дискретным, и воспроизводимым с четкостью 20% и точностью 80-120%.
64 1. Нижний предел количественного анализа (LLOQ) Самый низкий уровень кривой должен быть принят как стандарт квантификации, если соблюдены следующие условия: Реакция аналита на LLOQ должна быть проверена минимум в 5 случаях и сравнена с реакцией на чистую реакцию. Пик аналита (реакции) должен быть идентифицорованым, дискретным, и воспроизводимым с четкостью 20% и точностью 80-120%.
 65 2. Калибровочной кривой/Стандартной кривой/Реакция концентрации Должна быть использована простейшая модель, которая адекватно описывает взаимодействие реакция-концентрация. Должен быть оправдан выбор взвешивания и использования комплексного уравнения регрессии. Должны быть выполнены следующие условия при создании кривой: #20% отклонение LLOQ от номинальной концентрации #15% отклонение от стандартов, кроме LLOQ от номинальной концентрации По крайней мере 4 из 6 не нулевых стандартов должны соответствовать вышеуказанным критериям, в том числе LLOQ и эталоны высокой концентрации. Исключая стандарты не должны меняться модели.
65 2. Калибровочной кривой/Стандартной кривой/Реакция концентрации Должна быть использована простейшая модель, которая адекватно описывает взаимодействие реакция-концентрация. Должен быть оправдан выбор взвешивания и использования комплексного уравнения регрессии. Должны быть выполнены следующие условия при создании кривой: #20% отклонение LLOQ от номинальной концентрации #15% отклонение от стандартов, кроме LLOQ от номинальной концентрации По крайней мере 4 из 6 не нулевых стандартов должны соответствовать вышеуказанным критериям, в том числе LLOQ и эталоны высокой концентрации. Исключая стандарты не должны меняться модели.
 66 Глоссарий Точность: Степень близости определяемого номинального значения или истинное значение при определенных условиях. Также иногда называют достоверностью. Аналит: специфический измеряемый химический компонент, который может содержаться в наркотиках, биомолекулы или его производные, метаболиты, и/или деградация продукта в биологической матрице. Аналитическая работа: Полный набор аналитических и изучаемых образцов с соответствующим количеством стандартов и QCs для их проверки. Несколько работ могут быть завершены за один день, или одна работа может занять несколько дней.
66 Глоссарий Точность: Степень близости определяемого номинального значения или истинное значение при определенных условиях. Также иногда называют достоверностью. Аналит: специфический измеряемый химический компонент, который может содержаться в наркотиках, биомолекулы или его производные, метаболиты, и/или деградация продукта в биологической матрице. Аналитическая работа: Полный набор аналитических и изучаемых образцов с соответствующим количеством стандартов и QCs для их проверки. Несколько работ могут быть завершены за один день, или одна работа может занять несколько дней.
 67 Калибровочный стандарт: Биологические матрицы, в которых известно количество аналита. Калибровочные стандарты используются для построения калибровочной кривой, с помощью которых определяются концентрации аналита в QCs и в неизвестных образцах. Внутренний стандарт: тестовые соединения (на пример структурно подобранные аналоги) добавляются как калибровочные стандарты и известные образцы и постоянные концентрации для упрощения квантификации аналита. Предел обнаружения (LOD): Наименьшая концентрация аналита в биоаналитической процедуре может надежно отличить от его «фонового шума». Нижний предел квантификации (LLOQ): Наименьшее количество аналита в образце, который может быть определен в с соответствующей точность и аккуратностью.
67 Калибровочный стандарт: Биологические матрицы, в которых известно количество аналита. Калибровочные стандарты используются для построения калибровочной кривой, с помощью которых определяются концентрации аналита в QCs и в неизвестных образцах. Внутренний стандарт: тестовые соединения (на пример структурно подобранные аналоги) добавляются как калибровочные стандарты и известные образцы и постоянные концентрации для упрощения квантификации аналита. Предел обнаружения (LOD): Наименьшая концентрация аналита в биоаналитической процедуре может надежно отличить от его «фонового шума». Нижний предел квантификации (LLOQ): Наименьшее количество аналита в образце, который может быть определен в с соответствующей точность и аккуратностью.
 68 Эффект матрицы: Прямые или косвенные изменения или вмешательства в реакцию из-за случайного наличия аналитов или других мешающих веществ в образце. Метод: подробное описание всех процедур, используемых при анализе образца. Четкость: Близость совпадений (степень разброса) между серией исследований, отобранных из нескольких подобных однородных образцов по заданным условиям. Количественный диапазон: Диапазон концентраций, включающий ULOQ и LLOQ, которые могут быть надежными и воспроизводимыми с количественной точностью и точностью за счет соотношений концентрация-реакция.
68 Эффект матрицы: Прямые или косвенные изменения или вмешательства в реакцию из-за случайного наличия аналитов или других мешающих веществ в образце. Метод: подробное описание всех процедур, используемых при анализе образца. Четкость: Близость совпадений (степень разброса) между серией исследований, отобранных из нескольких подобных однородных образцов по заданным условиям. Количественный диапазон: Диапазон концентраций, включающий ULOQ и LLOQ, которые могут быть надежными и воспроизводимыми с количественной точностью и точностью за счет соотношений концентрация-реакция.
 69 Возмещение: Выборка эффективности аналитического процесса, формируется в процентах от известного количества аналита и осуществляется путем извлечения образца и проработки шагов методики. Воспроизводимость: Точность между двумя лабораториями. Она также представляет точность метода и при одинаковых условиях эксплуатации в течении короткого периода времени. Чистый: Образец биологической матрицы на котором нет аналитов и который используется для оценки специфических биоаналитических методов. Контроль качества образцов (QC): Образцы используются для мониторинга производительности биоаналитического метода, для оценки целостности и достоверности результатов неизвестных образцов из отдельных партий.
69 Возмещение: Выборка эффективности аналитического процесса, формируется в процентах от известного количества аналита и осуществляется путем извлечения образца и проработки шагов методики. Воспроизводимость: Точность между двумя лабораториями. Она также представляет точность метода и при одинаковых условиях эксплуатации в течении короткого периода времени. Чистый: Образец биологической матрицы на котором нет аналитов и который используется для оценки специфических биоаналитических методов. Контроль качества образцов (QC): Образцы используются для мониторинга производительности биоаналитического метода, для оценки целостности и достоверности результатов неизвестных образцов из отдельных партий.
 70 Селективность: Возможность биоаналитического метода измерять и различать наличие аналитов в компонентах. Стабильность: Химическая стабильность аналита из данных матрицы в определенных условиях в заданный промежуток времени. Стандартная кривая: Отношения между экспериментальными значениями отклика и аналитической концентрацией (также называется калибровочной кривой). Система пригодности: Определение инструментов производительности (например чувствительность и хроматографическое удерживание) по анализу эталоном до запуска аналитического пакета. Верхний предел количественного показателя (ULOQ): Большая величина аналита в образце, которая может быть определена с высокой точностью.
70 Селективность: Возможность биоаналитического метода измерять и различать наличие аналитов в компонентах. Стабильность: Химическая стабильность аналита из данных матрицы в определенных условиях в заданный промежуток времени. Стандартная кривая: Отношения между экспериментальными значениями отклика и аналитической концентрацией (также называется калибровочной кривой). Система пригодности: Определение инструментов производительности (например чувствительность и хроматографическое удерживание) по анализу эталоном до запуска аналитического пакета. Верхний предел количественного показателя (ULOQ): Большая величина аналита в образце, которая может быть определена с высокой точностью.
 71 Аттестация Полная аттестация: Создание всех параметров проверки для возможности анализа проб биоаналитическим методом для каждого вещества (аналита). Частичная аттестация: Модификация утвержденных биоаналитических методов, которые не обязательно требуют полной переаттестации. Перекрестная аттестация: Сопоставление контрольных параметров двух аналитических методов.
71 Аттестация Полная аттестация: Создание всех параметров проверки для возможности анализа проб биоаналитическим методом для каждого вещества (аналита). Частичная аттестация: Модификация утвержденных биоаналитических методов, которые не обязательно требуют полной переаттестации. Перекрестная аттестация: Сопоставление контрольных параметров двух аналитических методов.
 72
72
 73 Целью осуществления случайной выборки из партии или популяции с использованием вычислительной статистики, такое, как среднее из данных, является приближенный показатель к популяции. На сколько правильна статистика оценки базового значения всегда остается вопросом. Доверительный интервал решает этот вопрос, поскольку он обеспечивает диапазон значений, которые могут содержать параметры популяции. Доверительный интервал
73 Целью осуществления случайной выборки из партии или популяции с использованием вычислительной статистики, такое, как среднее из данных, является приближенный показатель к популяции. На сколько правильна статистика оценки базового значения всегда остается вопросом. Доверительный интервал решает этот вопрос, поскольку он обеспечивает диапазон значений, которые могут содержать параметры популяции. Доверительный интервал
 74 Доверительный интервал создается на доверительном уровне, таком как 95%, выбранном пользователем. Что то значит? Это значит, что если пробы одной и той же популяция брались неоднократно и интервальные оценки сделаны по каждому случаю, в результате интервалы показывают границы истинных параметров популяции примерно в 95% случаев. Достоверность исследования на уровне 1-alfa можно рассматривать как обратное значение уровня alfa. Доверительный интервал
74 Доверительный интервал создается на доверительном уровне, таком как 95%, выбранном пользователем. Что то значит? Это значит, что если пробы одной и той же популяция брались неоднократно и интервальные оценки сделаны по каждому случаю, в результате интервалы показывают границы истинных параметров популяции примерно в 95% случаев. Достоверность исследования на уровне 1-alfa можно рассматривать как обратное значение уровня alfa. Доверительный интервал
 75 Таким образом статистические тесты могут быть одно и двусторонними, доверительные интервалы также могут быть одно и двусторонними. Двусторонний доверительный интервал – границы параметров популяции «от» и «до». Односторонний доверительный интервал – границы параметров популяции либо ниже нижнего параметра, либо выше верхнего параметра. Пример двустороннего доверительного интервала. Доверительный интервал
75 Таким образом статистические тесты могут быть одно и двусторонними, доверительные интервалы также могут быть одно и двусторонними. Двусторонний доверительный интервал – границы параметров популяции «от» и «до». Односторонний доверительный интервал – границы параметров популяции либо ниже нижнего параметра, либо выше верхнего параметра. Пример двустороннего доверительного интервала. Доверительный интервал
 76 На пример, a 100% доверительный интервал для среднего значения нормальной популяции; Где средне выборочное, является верхним критическим значением от нормального стандартного распределения, которое находится в таблице нормального стандартного определения, где известно стандартное отклонение, и N является размером выборки. Доверительный интервал
76 На пример, a 100% доверительный интервал для среднего значения нормальной популяции; Где средне выборочное, является верхним критическим значением от нормального стандартного распределения, которое находится в таблице нормального стандартного определения, где известно стандартное отклонение, и N является размером выборки. Доверительный интервал
 77 Какова взаимосвязь между тестом и доверительным интервалом? В основном, для тестирования гипотезы есть эквивалентное утверждение о том, что значение параметра включено в доверительный интервал. На пример, рассматривая предыдущий пример ширины линий где фотошаблоны проверяются, чтобы их линии были имели средний размер 500 мкм. Нулевая и альтернативная гипотезы: H0: средняя ширина = 500 micrometers Ha: средняя ширина # 500 micrometers
77 Какова взаимосвязь между тестом и доверительным интервалом? В основном, для тестирования гипотезы есть эквивалентное утверждение о том, что значение параметра включено в доверительный интервал. На пример, рассматривая предыдущий пример ширины линий где фотошаблоны проверяются, чтобы их линии были имели средний размер 500 мкм. Нулевая и альтернативная гипотезы: H0: средняя ширина = 500 micrometers Ha: средняя ширина # 500 micrometers
 78 Какова взаимосвязь между тестом и доверительным интервалом? Для теста выборочное среднее рассчитывается из N ширины линий выбранной позиции по каждому фотошаблону. Для целей тестирования, предполагается, что стандартное отклонение, известно из долгой истории этого процесса. Статистика тестов рассчитывается из образцов статистик и нулевая гипотеза отвергается, если: где значения представлены из нормального распределения.
78 Какова взаимосвязь между тестом и доверительным интервалом? Для теста выборочное среднее рассчитывается из N ширины линий выбранной позиции по каждому фотошаблону. Для целей тестирования, предполагается, что стандартное отклонение, известно из долгой истории этого процесса. Статистика тестов рассчитывается из образцов статистик и нулевая гипотеза отвергается, если: где значения представлены из нормального распределения.
 79 Какова взаимосвязь между тестом и доверительным интервалом Немного математики и будет видно, что нулевая гипотеза не верна если и только если значение 500 micrometers не входит в доверительный интервал Эквивалент доверительного интервала. На самом деле, все значения, заключенные в этот интервал будут приняты в качестве нулевого значения для данного набора тестовых данных.
79 Какова взаимосвязь между тестом и доверительным интервалом Немного математики и будет видно, что нулевая гипотеза не верна если и только если значение 500 micrometers не входит в доверительный интервал Эквивалент доверительного интервала. На самом деле, все значения, заключенные в этот интервал будут приняты в качестве нулевого значения для данного набора тестовых данных.
 80 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Статистический тест способствует созданию механизма для принятия решений количественном о процессе или процессах. Целью является определение, достаточно ли существует доказательств чтобы отклонить предположение или гипотезу о процессе. Предположение называется «нулевой гипотезой». Не отклонение гипотезы может дать хороший результат если мы хотим продолжить работу, и если мы “верим" что «нулевая гипотеза» верна. Или это может дать разочаровывающий результат, возможно показывая, что у нас не хватает данных для того, чтобы “доказать" несостоятельность нулевой гипотезы.
80 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Статистический тест способствует созданию механизма для принятия решений количественном о процессе или процессах. Целью является определение, достаточно ли существует доказательств чтобы отклонить предположение или гипотезу о процессе. Предположение называется «нулевой гипотезой». Не отклонение гипотезы может дать хороший результат если мы хотим продолжить работу, и если мы “верим" что «нулевая гипотеза» верна. Или это может дать разочаровывающий результат, возможно показывая, что у нас не хватает данных для того, чтобы “доказать" несостоятельность нулевой гипотезы.
 81 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Классическое использование статистического теста происходит в процессе контрольной стадии. К примеру, предположим, что мы заинтересованы в обеспечении того, чтобы фотошаблоны в организации производственного процесса имели среднюю ширину 500 мкм. Нулевая гипотеза, в данном случае, это то, что средняя ширина равна 500 мкм. Неявным в этом заявлении является то, что нужен индикатор фотошаблона, который обозначает ширину линий, которые либо гораздо больше или гораздо меньше чем 500 мкм. Это приводит к альтернативной гипотезе, что ширина линии не менее 500 мкм. Это двусторонняя альтернатива, поскольку она предусматривает противоположное мнение; а именно, что ширина линий слишком мала или слишком большая.
81 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Классическое использование статистического теста происходит в процессе контрольной стадии. К примеру, предположим, что мы заинтересованы в обеспечении того, чтобы фотошаблоны в организации производственного процесса имели среднюю ширину 500 мкм. Нулевая гипотеза, в данном случае, это то, что средняя ширина равна 500 мкм. Неявным в этом заявлении является то, что нужен индикатор фотошаблона, который обозначает ширину линий, которые либо гораздо больше или гораздо меньше чем 500 мкм. Это приводит к альтернативной гипотезе, что ширина линии не менее 500 мкм. Это двусторонняя альтернатива, поскольку она предусматривает противоположное мнение; а именно, что ширина линий слишком мала или слишком большая.
 82 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Процедура тестирования происходит следующим образом. Ширина линий в произвольной позиции на фотошаблонах измеряются с помощью электронного сканирующего микроскопа. Тестовая статистика вычисляется из данных и снова тестируется в заранее определенной плоскости верхних и нижних значений. Если тестовая статистика больше верхнего критического значения или меньше нижнего критического значения, нулевая гипотеза отвергается, потому что есть доказательство того, что средняя ширина линий не 500 мкм.
82 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Процедура тестирования происходит следующим образом. Ширина линий в произвольной позиции на фотошаблонах измеряются с помощью электронного сканирующего микроскопа. Тестовая статистика вычисляется из данных и снова тестируется в заранее определенной плоскости верхних и нижних значений. Если тестовая статистика больше верхнего критического значения или меньше нижнего критического значения, нулевая гипотеза отвергается, потому что есть доказательство того, что средняя ширина линий не 500 мкм.
 83 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Нулевая и альтернативная гипотезы также могут быть односторонними. К примеру, предположение, что электролампы имеют среднюю продолжительность горения по крайней мере 500 часов, осуществляем тестирование программы. Нулевая гипотеза, в данном случае, предполагает, что жизнь лампочки больше или равна 500 часам. Альтернативная или дополнительная гипотеза предусматривает, что средняя продолжительность жизни лампочки меньше 500 часов. Сравниваем тестовую статистику с показателями нижней критической отметки, и если она меньше данного показателя, то нулевая гипотеза отвергается. Таким образом, статистический тест требует наличия двух гипотез, а именно: H0: нулевая гипотеза Ha: альтернативная гипотеза
83 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Нулевая и альтернативная гипотезы также могут быть односторонними. К примеру, предположение, что электролампы имеют среднюю продолжительность горения по крайней мере 500 часов, осуществляем тестирование программы. Нулевая гипотеза, в данном случае, предполагает, что жизнь лампочки больше или равна 500 часам. Альтернативная или дополнительная гипотеза предусматривает, что средняя продолжительность жизни лампочки меньше 500 часов. Сравниваем тестовую статистику с показателями нижней критической отметки, и если она меньше данного показателя, то нулевая гипотеза отвергается. Таким образом, статистический тест требует наличия двух гипотез, а именно: H0: нулевая гипотеза Ha: альтернативная гипотеза
 84 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Нулевая гипотеза – это то что кажется верным. Мы можем подозревать, что нулевая гипотеза верна, вот почему мы ее тестируем. Альтернативная гипотеза может, по факту, оказаться истинной. Процедура тестирования построена таким образом, что риск того, что нулевая гипотеза окажется не верной, когда она верна на самом деле, очень мал. Этот риск, часто упоминается как уровень значимости теста. При наличии теста с малыми данными, мы считаем, что на самом деле «доказали» что-то, когда мы опровергаем нулевую гипотезу.
84 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Нулевая гипотеза – это то что кажется верным. Мы можем подозревать, что нулевая гипотеза верна, вот почему мы ее тестируем. Альтернативная гипотеза может, по факту, оказаться истинной. Процедура тестирования построена таким образом, что риск того, что нулевая гипотеза окажется не верной, когда она верна на самом деле, очень мал. Этот риск, часто упоминается как уровень значимости теста. При наличии теста с малыми данными, мы считаем, что на самом деле «доказали» что-то, когда мы опровергаем нулевую гипотезу.
 85 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Угроза срыва отклонения нулевой гипотезы возможна, когда на самом деле она ложная и не выбрана пользователем, а определяется, как и следовало ожидать, от величины реального расхождения. Этот риск, обычно называют ошибкой второго рода. Большие расхождения между реальностью и нулевой гипотезой легче обнаружить и привести к небольшой ошибке второго рода; в то время как небольшие расхождения являются более трудными и могут привести к большим ошибкам второго рода. Кроме того, когда один риск возрастает, то другой уменьшается.
85 СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ Угроза срыва отклонения нулевой гипотезы возможна, когда на самом деле она ложная и не выбрана пользователем, а определяется, как и следовало ожидать, от величины реального расхождения. Этот риск, обычно называют ошибкой второго рода. Большие расхождения между реальностью и нулевой гипотезой легче обнаружить и привести к небольшой ошибке второго рода; в то время как небольшие расхождения являются более трудными и могут привести к большим ошибкам второго рода. Кроме того, когда один риск возрастает, то другой уменьшается.

